基于电力大数据的中国GDP 现时预测
孙 妮,潘 璠,肖娅晨,彭 放,周晓磊
(1.国家电网有限公司大数据中心,北京 100052;2.清华大学社会科学学院,北京 100084)
一、引言
无论政府经济政策的制定,还是企业经营策略的选择,都需要及时、准确的了解当前宏观经济形势。GDP 是刻画宏观经济形势的最核心经济指标,一直以来备受各经济主体的关注。尽管GDP 的预测是许多学者及机构研究的重点,但传统预测技术的不足以及常用经济统计数据的滞后限制了GDP 预测的时效性与精准度。伴随着人类社会步入大数据时代,基于大数据的宏观经济现时预测受到越来越多的重视。电力数据与经济活动密切相关是经济的“晴雨表”,本文将利用电力大数据实时、客观、颗粒度细等优势实现对GDP 更精准的现时预测,以为政府、企业的决策提供及时可靠的数据支撑。
二、文献综述
就现有文献来看,当前的宏观经济预测模型依据其是否可以直接应用不同频率的数据可分为同频数据预测模型和混频数据预测模型两类。同频数据预测模型的预测基于同频数据进行,高频数据应该转化为低频数据。当前Sims(1980)[1]提出的VAR模型是各国中央银行构建宏观经济预测模型的基础(张劲帆等,2018)[2],国内许多宏观经济预测模型的构建也是基于VAR 进行,如中国人民银行的季度VAR模型及Logit-VAR 月度模型,周建和况明(2015)[3]建立的中型宏观系统季度同频贝叶斯模型。随着深度学习技术的发展,国内有学者利用深度学习预测GDP,如肖争艳等(2020)[4]、徐映梅和陈尧(2021)[5]利用LSTM模型就GDP 进行预测并取得较好的预测效果。
混频数据预测模型能够直接基于混频数据进行宏观经济分析,这意味着预测时可以利用高频数据提供的当期信息,如此预测的准确性与时效性都将得以提高。当前应用较多的混频数据模型为Ghysels等(2005)[6]提出的混频数据抽样模型(MIDAS),国内有部分学者利用该模型开展GDP 的预测研究。刘汉和刘金全(2011)[7]以消费、投资、出口作为解释变量的研究结果表明,就中国宏观经济的短期预测而言MIDAS模型比同频数据模型具有显著更佳的精确性,而且包含自回归项的MIDAS模型较之于不包含自回归项的MIDAS模型具有更佳的预测精确性。郑挺国和尚玉皇(2013)[8]基于股票波动率、人民币实际有效汇率等金融变量的研究支持了刘汉和刘金全(2011)[7]的上述研究结论,而且发现基于包含自回归项的MIDAS模型的预测组合的精确性占优。王维国和于扬(2016)[9]针对等权重等四类不同权重下MIDAS预测组合精确性的研究发现,基于BIC 构建的MIDAS模型预测组合在短期预测中表现最优。
近年来国内学者开始关注基于新兴数据的GDP 预测,如刘涛雄和徐晓飞(2015)[10]、何强和董志勇(2020)[11]利用互联网大数据的预测,范强等(2019)[12]、卢秀等(2020)[13]利用灯光数据的预测。然而当前鲜有学者利用电力大数据预测GDP,探究电力大数据预测宏观经济形势的能力。许多学者就电力消费与经济发展关系的研究表明,尽管研究方法与数据存在差异,但大多数研究表明电力消费增长与经济增长间在短期存在因果关系,在长期存在均衡关系(杨东伟,2013)[14]。作为社会经济活动的结果,电力数据是必然可以反映经济发展的情况,成为预测宏观经济的有效指标。
三、研究方法
1.单变量MIDAS模型。MIDAS模型由Ghysels等(2005)[6]首次提出,其主要特点为通过权重函数B(L1/m;θ)将高频数据直接引入模型避免了高频数据的低频化处理,表达形式如式(1)所示。
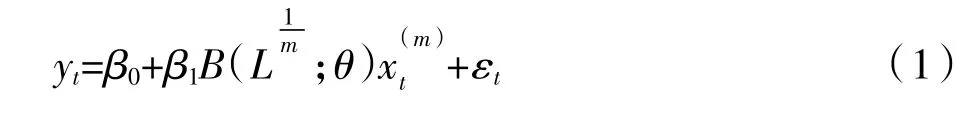
其中,m表示的是高频数据与低频数据间频率的倍差,为加权函数,其中表示高频数据的滞后算子0,1,…,K,t=1,2,…,T),K为所设定的高频数据的最大滞后阶数。
基于式(1)可得相应的预测模型MIDAS(m,K,h)如下:
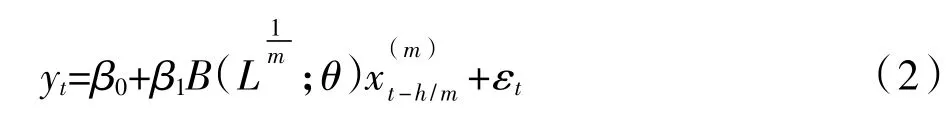
其中,h表示预测步长。就本文的分析而言,GDP 增长率为季度数据频率较低,而选择的解释变量为月度数据频率较高,在这种情形下当h小于3(此时在预测GDP 时用到了解释变量季度的一部分信息)时即为现时预测。h等于0、1、2 意味着在现时预测中分别用到季度3 个月、2 个月及1 个月的月度数据。关于权重函数我们选择指数Almon 多项式函数。
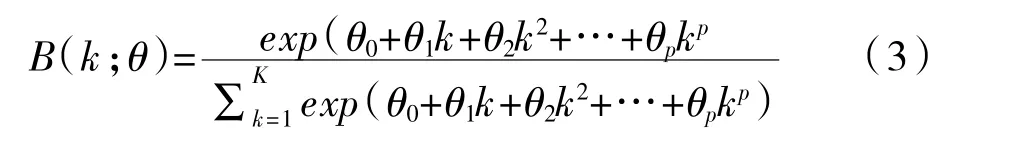
文中将基于常用的两参数指数Almon 多项式函数进行分析,同时我们还将参考Clements 和Galva軇o(2008)[15]的做法令θ1≤300,θ2<0。此处对指数Almon 多项式参数限制一方面可以确保分析所需的权重得到满足,另一方面可以确保权重为正并使得方差的误差逼近于零(刘汉和刘金全,2011)[7]。
2.MIDAS-AR模型。宏观经济变量一般存在惯性,因此在预测宏观经济变量时有必要将其滞后项作为解释变量引入单变量MIDAS模型。带有p阶自回归滞后项的MIDAS-AR模型可表示如下。
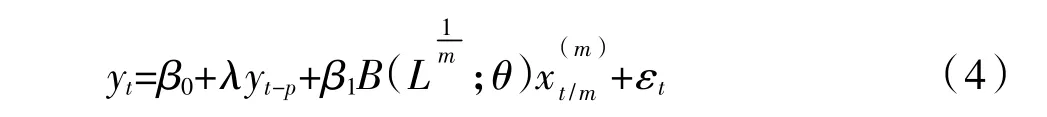
如式(5)给出了相应的预测模型MIDAS(m,K,h)-AR(p):
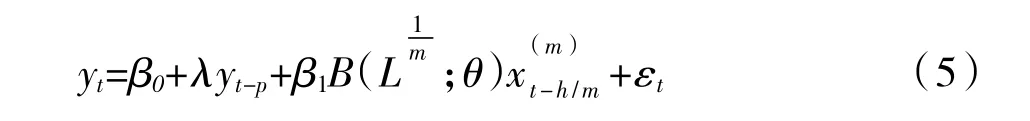
3.M(n)-MIDAS模型。宏观经济变量处于复杂的经济系统中,受到诸多经济因素的影响,故有必要采用多变量MIDAS模型进行预测。基于上述的式(1)和式(4)可以得到相应的多变量模型M(n)-MIDAS和M(n)-MIDAS-AR,如下的式(6)和式(7)为相应的表达式:

其中,n表示模型中解释变量的数目。
由式(6)和式(7)可进一步得到相应的预测模型M(n)-MIDAS(m,K,h)、M(n)-MIDAS(m,K,h)-AR(p)如下:
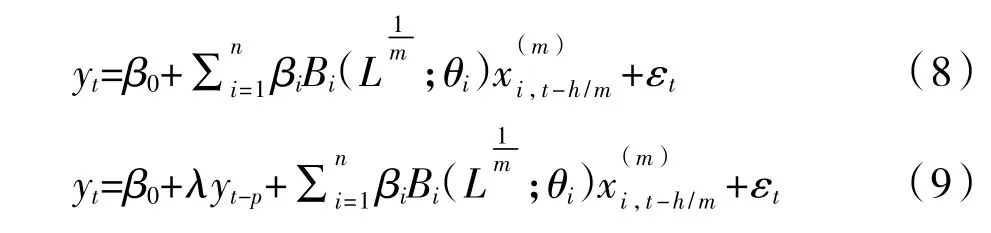
4.预测组合。当被预测目标受多个解释变量影响时,数据样本容量及过多的待估参数将限制M(n)-MIDAS的预测效果。这种情况下,预测组合(Forecast combination)是一个常用的解决方法。Timmermann(2006)[16]对预测组合方法进行总结,认为通过一定的权重将若干模型的预测结果组合起来可以提高预测精度。基于n个模型的预测组合可表示如公式(10)所示。

其中,表示t时刻的第i个预测结果,wi,t表示组合预测中第i个预测结果的权重,本文选择比较常用的BIC 权重。

其中,BICi表示第i个预测结果的BIC信息准则值。
四、实证分析
(一)基准预测模型与数据说明
1.基准模型。为比较分析不同预测模型及预测方法组合的优劣程度,本文选ARMA(Autoregressive moving average model,自回归滑动平均模型)作为基准模型,采用MSFE(mean squared forecast errors,均方预测误差)测度模型的预测效果,MSFE 的计算公式如(12)所示。
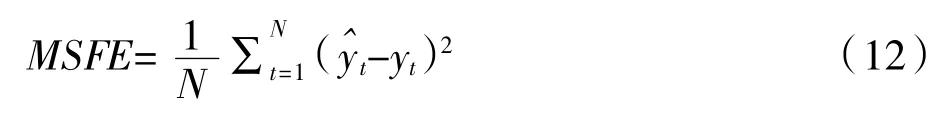
其中,和yt分别表示预测值和实际值。进一步的本文用均方预测误差的比值(ratio ofmean squared forecast errors,rMSFE)来衡量预测模型的优劣,rMSFE可以用公式(13)表示。
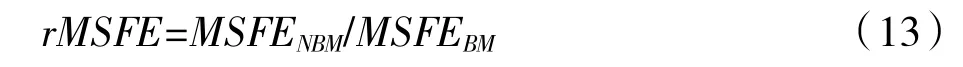
公式(13)中,MSFENBM和MSFEBM分别表示所用非基准模型和基准预测模型的MSFE值。若rMSFE小于1 则意味着非基准模型有更好的预测准确度,而且比值越小意味着准确度越高。
2.数据说明。本文的预测基于电力大数据和传统的经济统计数据两类数据开展。文中所用购电大数据为通过加总国内26 个省5 亿多用户的用电数据而得到的月度同比购电数据指标,包含全行业及其三种不同划分下的电力数据指标共65 个。第一种划分按产业进行,即将整个行业划分为第一产业、第二产业、第三产业三类。第二种划分将整个行业分为农林牧渔、工业、建筑业等八类。第三种划分为对第二种划分的进一步分类,此处不再给出具体类别。电力数据均来自国家电网有限公司大数据中心,时间跨度为2014 年1 月至2019 年12 月。
为了充分比较说明电力大数据在GDP 现时预测中的价值,文中还将选择传统的经济统计数据作为解释变量。关于经济统计变量的选择,考虑到消费、投资、出口是影响经济增长的重要因素故将其作为解释变量,同时选择社会消费品零售总额月度同比增速、固定资产投资完成额月度同比增速以及出口总额月度同比增速作为相应的测度指标。本文所用经济统计数据均来源于国家统计局,其中季度GDP 增长率的时间区间为2000 年第一季度至2019年第四季度,其他经济变量同比数据的时间区间为2000 年1 月至2019 年12 月。
为得到更加精确的预测结果,本文首先采用X12 方法对所有数据进行季节性调整进一步消除季节性,然后采用ADF 方法检验季调后时间序列的平稳性,若时间序列不平稳则进行差分处理直至序列平稳。限于篇幅本文不再给出平稳性检验及差分次数的相应结果。
(二)基于电力数据的预测分析
本部分基于电力数据和MIDAS模型现时预测GDP,预测采用移动窗口和累积窗口两种方法,样本外预测区间为2018 年第四季度至2019 年第四季度。为充分分析电力数据的现时预测效果,本文不仅分析了不同划分下分类指标预测组合的预测效果,对第二、三两种划分。还给出了基于各划分下所有分类指标所提取动态因子的预测效果以及基于因子的预测组合的预测效果。限于篇幅文中将不再给出第二、三两种划分下各分类电力数据指标的预测效果。
1.单变量MIDAS及其预测组合的效果分析。鉴于文中所用电力大数据的样本较少,在应用MIDAS模型时我们仅考虑最大滞后阶数为6 和9 两种情况。根据预测结果,当最大滞后阶数为6 时MIDAS具有更优的预测效果。限于篇幅如下仅给出滞后阶数为6 时现时预测的rMSFE,相关预测结果如表1、表2、表3 所示。表1 给出了全行业、各产业总购电指标的预测rMSFE,以及三个产业预测组合的rMSFE。表2、表3 分别给出了第二划分和第三划分下相应分类指标预测组合、因子以及因子预测组合的预测rMSFE。
比较分析表1、表2、表3 中的rMSFE值可以得出如下结论:第一,所有预测的rMSFE值均小于1,这意味着基于ARMA模型并不能得到最优的预测结果,即仅仅利用GDP 历史信息的预测效果不是最优的。第二,就总量指标与其细分指标预测组合的预测效果来看,预测组合的精准度更佳。此外,比较三种划分下预测组合的效果可知,第三种划分明显优于第二种划分和第一种划分,而第二种划分优于第一种划分。第三,就细分指标预测组合与因子预测组合的预测效果来看,基于细分指标预测组合的精准度更佳。此外,比较两种划分下因子预测组合的预测效果可知,总体来看第二种划分下预测效果更优。
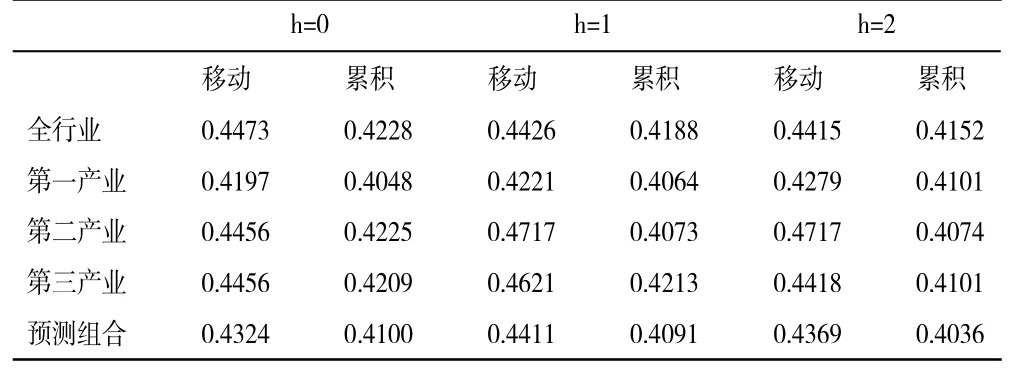
表1 基于全行业第一种划分现时预测GDP 的rMSFE
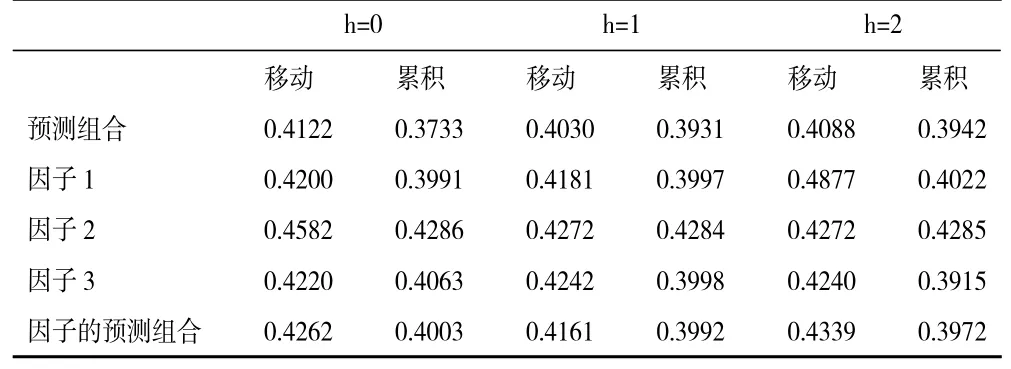
表2 基于全行业第二种划分现时预测GDP 的rMSFE
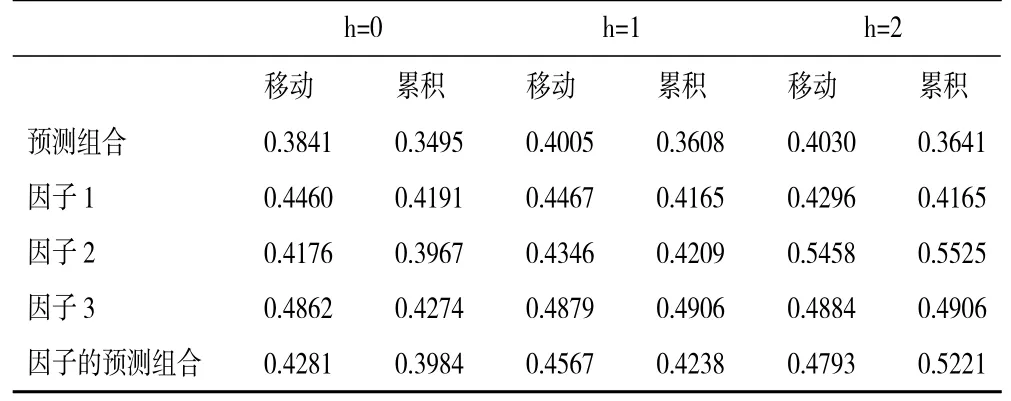
表3 基于全行业第三种划分现时预测GDP 的rMSFE
2.单变量MIDAS-AR及其预测组合的效果分析。本部分利用分别引入1 阶及4 阶滞后自回归项的MIDAS-AR模型进行预测,根据预测结果,当引入4 阶自回归滞后项、最大滞后阶数为6 时MIDASAR模型的预测效果更优,如表4、表5、表6 给出了相应的预测结果。
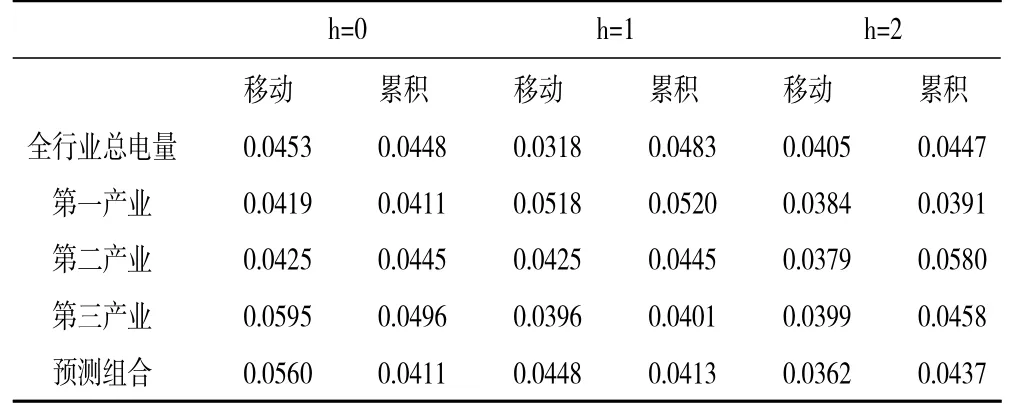
表4 全行业第三种划分现时预测GDP 的rMSFE
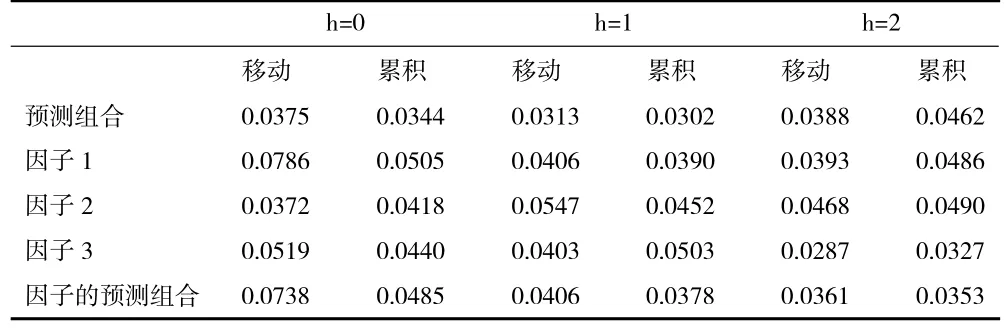
表5 基于全行业第二种划分现时预测GDP 的rMSFE
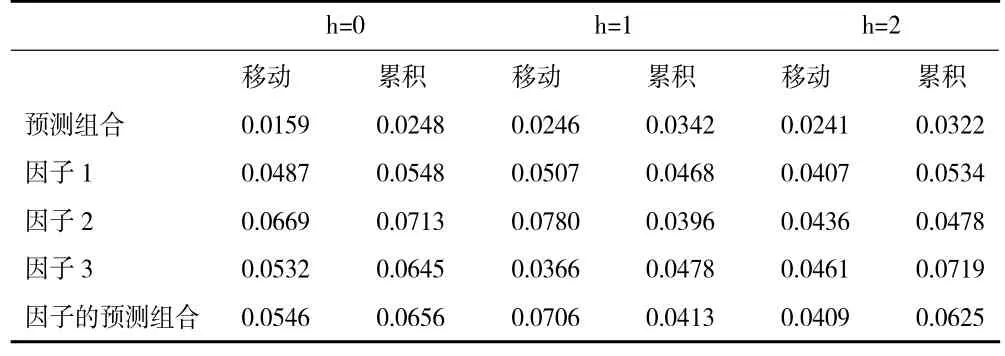
表6 基于全行业第三种划分现时预测GDP 的rMSFE
比较分析表4、表5、表6 中的rMSFE值可以得出如下结论:第一,所有预测的rMSFE值均小于1,这意味着基于ARMA模型并不能得到最优的预测结果,即仅仅利用GDP 历史信息的预测效果不是最优的。第二,就总量指标与其细分指标预测组合的预测效果来看,总量指标的预测效果未必优于其细分指标预测组合的预测效果,预测组合的预测效果可能显著占优。比较表4、表5、表6 中预测组合的效果可以发现,表6 中预测组合的rMSFE值明显小于表4、表5 中rMSFE值,同时也明显小于全行业总电量相应的rMSFE值,即对总量更细划分的预测组合具有更佳的预测效果。第三,关于细分指标预测组合与因子预测组合的预测效果,总体而言基于细分指标的预测组合拥有更佳的精准度。
关于MIDAS模型与MIDAS-AR模型预测效果,对比表1、表2、表3 中rMSFE的值与表4、表5、表6 中rMSFE的值可以发现,单变量MIDAS-AR模型具有更佳的精准度。这与刘汉和刘金全(2011)[7]以及郑挺国和尚玉皇(2013)[8]的研究结论相一致,进一步支持了他们的结论。
(三)电力大数据的预测能力分析
本部分将就电力大数据和传统经济统计指标现时预测GDP 同比增长率中的预测效果进行比较。我们基于分别引入1 阶及4 阶滞后自回归项的MIDAS-AR模型分析经济统计指标的现时预测效果,根据结果发现引入4 阶滞后自回归项时的预测效果最佳。限于篇幅文中仅给出包含4 阶自回归滞后项的MIDAS-AR模型预测结果,相应的预测rMSFE结果详见如表7 所示。表7 不仅呈现分别基于消费、投资、出口的GDP 现时预测结果,还给出了基于消费、投资、出口的预测组合以及多元MIDAS模型的预测结果。可以发现,较之于消费、投资、出口,基于电力数据的预测效果全部占优。这表明就GDP 的现时预测而言电力数据包含更多有用的信息。另外,还可以发现消费、投资的预测效果明显的优于出口,而且多元MIDAS模型的预测效果明显优于单变量MIDAS模型及其预测组合的预测效果。
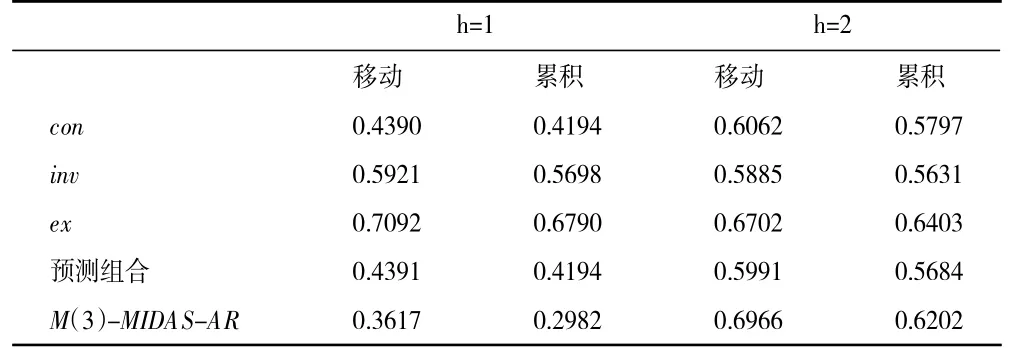
表7 基于消费、投资、出口现时预测GDP 的rMSFE
五、主要结论
对宏观经济形势进行更加及时准确的预测,不仅是宏观经济研究的重要领域,也是各经济主体普遍关注的重要内容。本文充分利用电力大数据实时准确、颗粒度细等优势,探究电力大数据在宏观经济现时预测中的能力,从宏观经济预测的角度进一步展示了电力数据经济“晴雨表”的作用。综合实证分析的结果可得出如下结论:一是单变量MIDASAR模型的预测效果要显著的优于单变量MIDAS模型的预测效果,这与刘汉和刘金全(2011)[7]以及郑挺国和尚玉皇(2013)[8]的研究结论相一致。二是相对于包含一阶自回归项的MIDAS-AR模型,包含四阶自回归项的MIDAS-AR模型具有更优的现时预测效果;三是比较电力数据指标与消费、投资、出口的GDP 现时预测效果发现,电力数据指标的预测能力显著占优;四是通过比较电力数据总量指标与其分量指标预测组合的预测效果发现,预测组合具有更佳的现时预测效果。

