一种子阵降维带约束指向的抗干扰方法*

王晓洪，佟 力，毛新胜

（1.成都天奥信息科技有限公司，四川 成都 610041；2.中电科航空电子有限公司，四川 成都 610041）

0 引言

近年来，我国导航产业迅猛发展，为了解决卫星导航信号易受干扰的问题，我国也在大力研究自适应阵列抗干扰[1-6]技术。面临复杂电磁环境，单纯的任意一种抗干扰技术已经显得能力不足。时域、频域滤波不能对抗宽带干扰，空域滤波虽然对宽带信号具备很好的抑制能力，但由于阵列天线个数有限，能抑制的干扰数目受限；因此，可采用多域联合处理的抗干扰技术，充分发挥各种方法的优势，提高设备的抗干扰性能。

目前，一般工程上常采用的是空时联合抗干扰技术[7-9]，而实现上采用迭代算法（Least Mean Square，LMS），降低其实现难度，但是这样能达到的效果还是比较有限，并且还牺牲了算法的一部分性能。此外，随着阵列个数的增加，如相控制阵天线有上千个天线单元，使得即使采用LMS 这样的迭代算法，也难工程应用，从而空时联合抗干扰技术在大规模阵列天线上的应用受到限制。随着相控阵技术的发展，目前对于大规模相控阵天线的抗干扰应用需求也越来越大，而传统的空时联合抗干扰算法不能满足大规模相控阵天线的工程应用 要求。

空时联合抗干扰技术要求的实时处理能力高，因此一般都是采用现场可编程门阵列（Field Programmable Gate Array，FPGA）这样的芯片来进行算法的实现，而基于FPGA 芯片的设计中，资源越多算法的反而实时性越好，相反资源越少算法的反而实时性越差；因此，对于空时联合抗干扰技术来说，尤其是无法实现基于采样矩阵直接求逆（Sample Matrix Inversion，SMI）[10-12]算法的工程 应用。

本文针对空时联合抗干扰技术在大规模阵列天线应用上的技术瓶颈，提出一种基于子阵降维带约束指向的抗干扰方法。该方法在空域进行处理，采用阵元级进行子阵合成，从而实现空间维度进行降维处理的目的，达到减小算法工程应用难度，使得算法基于硬件设计可工程应用，突破SMI 算法在大规模阵列天线上的应用瓶颈，满足其算法超高精度要求。

1 子阵降维抗干扰技术

子阵降维抗干扰技术，算法分为子阵形成和抗干扰两个部分。子阵形成可以根据子阵内某一个阵元所在空间位置进行合成形成指向不同方向的子阵，也可以以一个固定空间方向进行合成形成指向同一个方向的子阵。抗干扰采用空时联合自适应抗干扰方法，具体实现上采用基于采样数据协方差矩阵求逆的算法。

1.1 子阵内数据的合成

子阵形成是对子阵中各阵元数据的合成，即确定长度为M的合成向量，M为子阵内的阵元个数。无论是根据子阵内某一个阵元所在空间位置还是以一个固定空间方向进行合成，都是利用指向的位置信息(θ,φ)形成合成向量，其中θ为俯仰角，φ为方位角。根据位置信息生成阵元合成的导向矢量，计算公式如下：

式中：λ代表中心频点对应的波长；(xm,ym,zm)表示阵元m的坐标值。从而得到M个阵元的合成向 量为：

1.2 空时抗干扰技术

空时阵列处理器结构见图1，其中T为抽头间的时间延迟，抗干扰权值为：

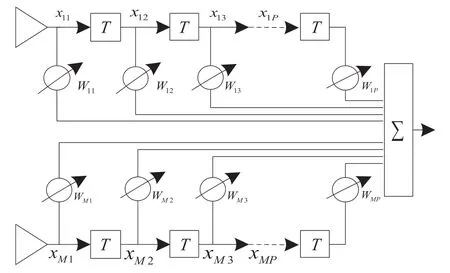
图1 空时联合阵列处理结构

抗干扰权值W通过可通过最小噪声方差准则[13-14]获得，即使阵列输出功率最小来选择最优价权矢量，为避免出现权值为零的情况，需加相应的约束条件。常用的约束方法为保证有用信号无失真通过，也就是阵列对有用信号的响应为常数。因此最小噪声方差准则的代价函数为：

式中：S(θ,φ)为导向矢量；θ为方位角；φ为俯仰角；R=E{x(n)x(n)H}为子阵接收信号自相关矩阵，这里的x(n)为子阵数据，而传统方式为阵元数据。对基于SMI 算法，最优解为：

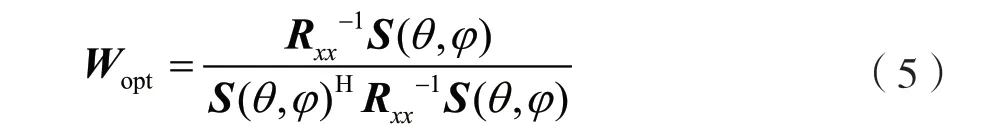
式（5）表示最优波束形成器即为最小方差无失真响应（Minimum Variance Distortionless Response，MVDR）波束形成器。

在监督机制建设中要重点强化企业的成本监督和相关管理工作，要以成本作为监督的目标，理顺企业生产、管理的经济关系，从成本控制的角度构建起有针对性、可执行的监督平台和监督制度，真正将监督工作的重点放在对企业各项成本的控制工作上，提升企业成本管理、运营管理的效率，打造企业在生产、管理和经营上的经济、组织与成本优势。

2 子阵降维多波束算法

数字多波束算法在抗干扰的同时还能对期望方向上的有用信号进行保护，目前工程上常用数字多波束算法停留在阵元级，本文针对子阵级进行数字多波束算法的研究。由前面可知子阵内阵元数据的合成有两种方式，因此对不同的子阵形成方式就会有不同子阵级数字多波束算法。基于子阵内某一个阵元所在空间位置形成的子阵级数字多波束算法简称，后约束子阵级多波束算法。基于以一个固定空间方向进行合成形成指向同一个方向的子阵级数字多波束算法，简称为先约束子阵级多波束算法。

2.1 后约束子阵级多波束算法

假设有N个阵元，以任意一个阵元为原点建立坐标系，每个阵元的坐标位置为pm(xm,ym,zm)，m=1,2,…,N。基于子阵内某一个阵元所在空间位置形成子阵，利用子阵内数据合成的方法，共形成M个子阵，每个子阵包含K=N/M个阵元，每个子阵的坐标与合成子阵选择的参考阵元的位置坐标一致。

采用MVDR 算法，即利用式（5）计算最优权值，首先需要计算基于子阵的期望方向上的导向矢量S(θ,φ)。首先，根据式（1），利用子阵的坐标，即合成子阵选择的参考阵元的位置坐标，和期望方向的方位θ和俯仰φ得到来波信号的角度值；其次，利用（2）得到导向矢量S(θ,φ)；最后，利用子阵数据得到采样矩阵Rxx。通过以上方式就完成了后约束子阵级多波束算法。

2.2 先约束子阵级多波束算法

先约束子阵级多波束算法也是根据公式（5）计算权值Wopt。式（5）中设计到子阵之间导向向量S(θ,φ)的计算与后约束的不同，从子阵数据的合成方式可以看出在阵元合成子阵过程中，所有子阵的波束方向都是指向了同一方向，因此式（5）中的S(θ,φ)可简化为全1 的导向向量，即S(θ,φ)=[1,1,…,1]'，因此不需要再计算子阵之间带约束的导向向量，算法得到了简化。根据式（5）计算当S(θ,φ)=[1,1,…,1]'时即为子阵指向目标方向带约束指向的抗干扰权值。

从上面分析可知先约束子阵级多波束算法较后约束子阵级抗干扰算法的实现方法变得简单了。主要是省去了MVDR 算法中导向矢量的生成，而且对于全一的导向矢量在计算带约束抗干扰权值时也变简单了，省去了式（5）矩阵与导向矢量S(θ,φ)相乘运算中的乘法运算，只有加法运算。

3 算法仿真与分析

3.1 仿真场景

设计3 组实验考察在低、中、高干扰目标场景下抗干扰性能。各实验均产生二相相移键控（Binary Phase Shift Keying，BPSK）信号作为干扰，载频1 268 MHz，码速率10 Mc/s，信息符号随机生成，阵元个数16 个，阵元间距半波长，根升余弦滚降系数设置为0.35，样本数取512 个样本点，绘制方向图的网格步进为0.1°。实验中，阵元幅度误差随机生成，并服从-0.5～0.5 dB 的均匀分布；阵元相位误差随机生成，并服从-5°～5°的均匀分布；其余参数如表1 所示。

表1 实验参数设置

3.2 干扰抑制和波束保护性能分析

3.2.1 干扰抑制性能分析

分别对基于阵元和子阵级的多波束抗干扰进行仿真对比。由于先约束和后约束从原理上来说是一致的，故仿真的时候就只针对先约束子阵级多波束方法进行仿真。干扰来向（60°,10°），仿真结果见图2 和图3；干扰来向（60°,45°），仿真结果见图4 和图5；干扰来向（60°,80°），仿真结果见图6和图7。

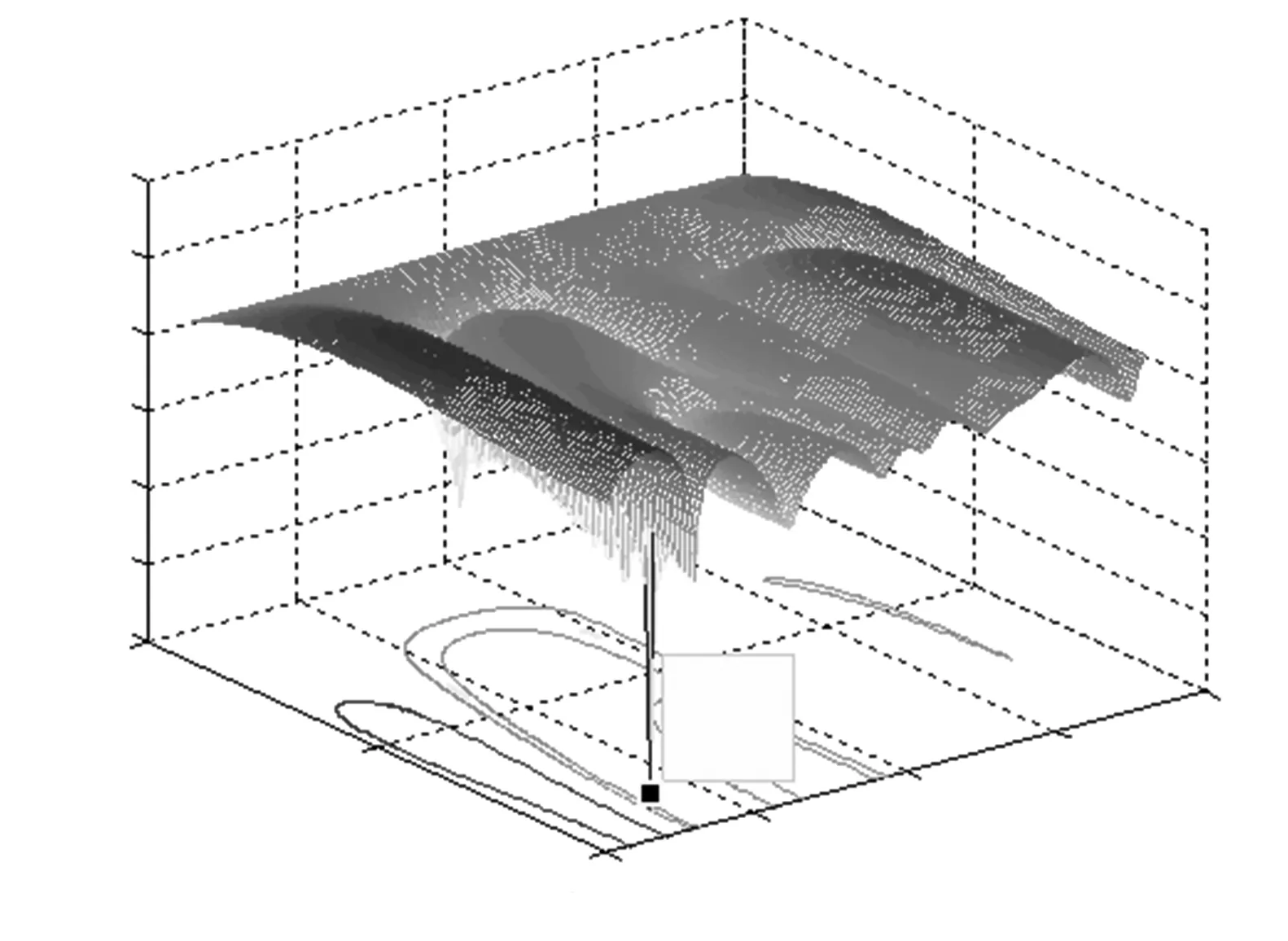
图2 阵元多波束抗干扰方向

图3 子阵多波束抗干扰方向

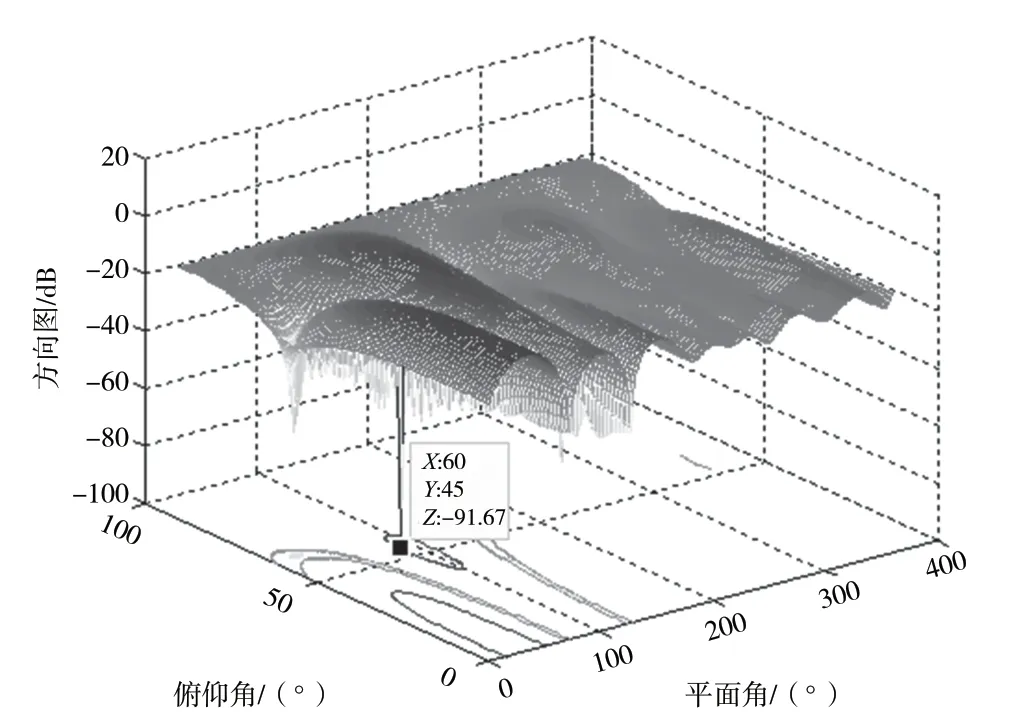
图4 阵元多波束抗干扰方向

图5 子阵多波束抗干扰方向

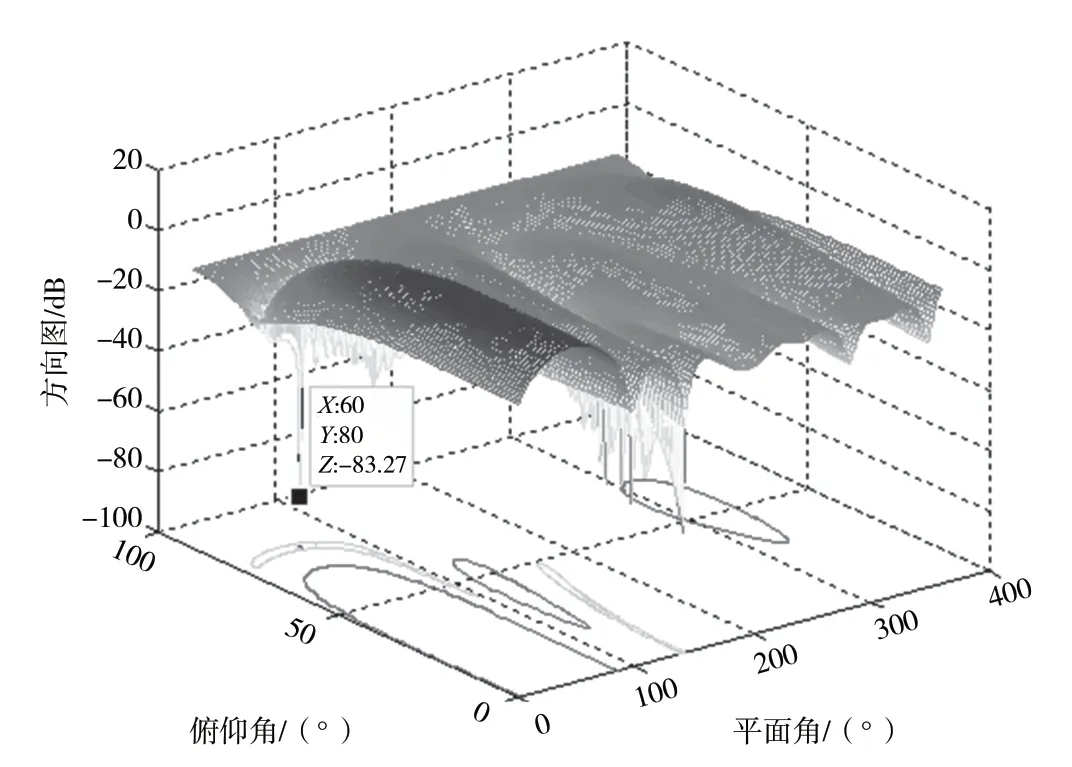
图7 子阵多波束抗干扰方向

3.2.2 波束保护性能分析

分别对基于阵元和子阵级抗的波束保护性能进行仿真对比。同理子阵级也是只对先约束子阵级多波束方法进行仿真，信号来向（45°,10°）的仿真结果见图8、图9 和图10。

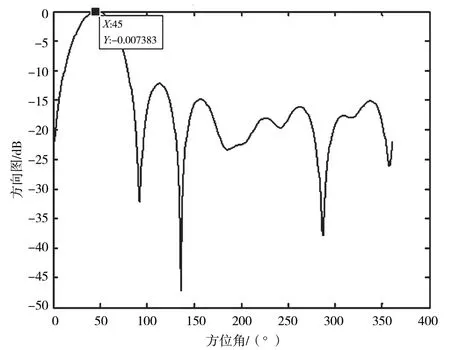
图8 阵元级二维波束方向

图9 子阵级二维波束方向图抗干扰方向

图10 波束增益对比误差

从图8 和图9 的方向图可以看出，本文方法在方位45°上形成了有效的波束保护。从图8 可以看出两种方式下形成的增益误差不超过0.45 dB。仿真结果上验证了基于阵元和子阵级波束保护性能的有效性。

4 结语

由于基于阵列天线的空时联合抗干扰技术的算法在工程应用中有着较大的实现难度，尤其是对于大型阵列天线，随着天线个数的增加使得其算法实现成技术瓶颈，限制了其技术的在大型阵列天线如相控阵上的应用。如何降低其实现难度成为技术应用的关键，而大部分研究都是围绕算法实现本身去思考，如LMS 算法。因此需要从最前端进行难度的降低。本文提出了一种子阵降维带约束的抗干扰算法，此算法是基于MVDR 算法原理的基础上得到的，并利用阵元级进行子阵合成，从而减少阵元个数，达到保证抗干扰性能的同时又能保证阵列增益。相比阵元级的方案，该方法的所需要的硬件资源有明显优势。

基于以上分析可以看出尤其是对于大型阵列天线来说，基于子阵降维带约束指向抗干扰方法具有明显的优势，且可工程化，而传统阵元级的方式工程化实现难度大，基本不可工程化。仿真结果验证了算法的抗干扰性能及波束保护性有效性，无论是先约束子阵多波束算法还是后约束子阵多波束算法，相对阵元级的处理其算法的性能并没有下降，同样可达到与阵元级算法相同的性能，但是却降低了算法实现的复杂度；因此，阵列抗干扰技术对于相控阵天线可工程化应用。