能量站辅助自持系统的隐蔽通信*

王冠杰，王易达，汪 鹏，石 会，关 宇

（1.陆军工程大学，江苏 南京 210007；2.军事科学院 系统工程学院，北京 100091）

0 引言

越来越多新颖的物联网设备大规模普及应用，给信息社会带来巨大便捷的同时，也带来了诸多挑战。大多数物联网设备由能量受限的传感器节点组成，而维持这些设备的工作时长都受制于自身有限的电量。在此背景下，通过部署能量站辅助自持系统通信是一种有效的解决办法，可以延长无线节点的使用寿命[1]。然而，由于无线信道天然的广播性，信息在传输过程中也会暴露给潜在的恶意能量接收器[2]，导致信息传输安全性受到巨大威胁。为确保信息传输的安全可靠，通常采用传统密码学技术对信息传输进行加解密。但是，传统的加解密技术并不总是适用于物联网设备应用场景，因为传统加解密硬件在加解密时需要消耗大量的资源，而对于自身体积较小、电量有限的物联网设备来说并不适用[3]。因此，可以考虑采用能量站辅助自持通信系统下的新型安全传输方案。

近年来，物理层安全利用无线信道自身的特性确保通信安全逐渐成为一种可选择的方案。具体来说，在能量站辅助自持系统通信方面，文献[4-5]通过能量站提供的能量信号、天线选择和波束赋形技术，可确保传输信息不被窃听者获取。然而，仅仅保护传输内容是无法提供更高等级的通信安全，需要通过隐藏通信行为即隐蔽通信来实现，目标是保证合法用户之间的通信，同时在监听者的检测下隐藏已有的通信行为[6]。基于前期的成果[7]，文献[8-9]研究了无线供能系统在多跳中继网络中的隐蔽通信。上述研究成果主要集中用于下行传输，但是在物联网设备运行中，下行传输的吞吐量远远低于上行传输[10]，尤其在能量站辅助自持系统通信网络中。本文创新地提出了采用能量站辅助自持系统隐蔽通信传输的方案。

本文研究能量站辅助自持系统的安全传输模型，利用无线信道不确定性实现隐蔽通信的方案，研究了能量受限约束条件下通信隐蔽性速率最大化问题，并推导出最小错判概率和时间分配因子闭式表达式，以衡量所提隐蔽通信方案的隐蔽性，并得到了最优信息发送速率。

1 系统模型

1.1 应用场景与假设条件

本文提出一个自持隐蔽通信系统。该系统包含1 个能量站、1 个监听者、1 个能量受限发送机以及1 个接收机。每个节点均为单天线设备。通信持续时间相互独立，且每个时隙以T划分。能量站-监听者、发送机-接收机、能量站-发送机、能量站-接收机、发送机-监听者的信道分别表示为hbw、htr、hbt、hbr、htw；能量站-监听者、发送机-接收机信道服从准静态瑞利衰落，相应的信道增益在每个时隙内不变，但在各时隙上独立变化；信道增益的均值为1/λpq，其中pq∈{bw,tr}。

能量受限的发送机需要在能量站的辅助供能下向接收机传输机密信息。此外，监听者作为非法接收方，试图检测发送机的通信行为。为隐藏发送机-接收机之间的合法通信，能量站持续发送含有人工噪声的电磁能量信号，为发送机提供能量的同时混淆监听者的检测通信新行为。

假设能量站的发送功率公开且固定为Pb，能量站为给发送机提供稳定能量传输，其信道hbt特性主要由视距（Line-of-Sight，LoS）成分决定。发送机在躲避监听者检测的情况下，利用从能量站采集的能量，秘密地将信息发送给接收机。考虑最糟糕的情况，监听者潜伏在发送机视距信道上进行监听，即htw也符合LoS 信道特性。

1.2 能量采集

图1 为本文采用的时间分配示意图。利用文献[11]中先采集后发送（Harvest-Then-Transmit，HTT）的协议，一个相干时隙T分成(1-α)T与αT两个子时隙，其中0 ＜α＜1 表示时间分配因子。在(1-α)T子时隙中，发送机从能量站发送的能量信号中采集能量；在αT子时隙中，发送机利用采集的能量发送隐蔽信息至接收机。

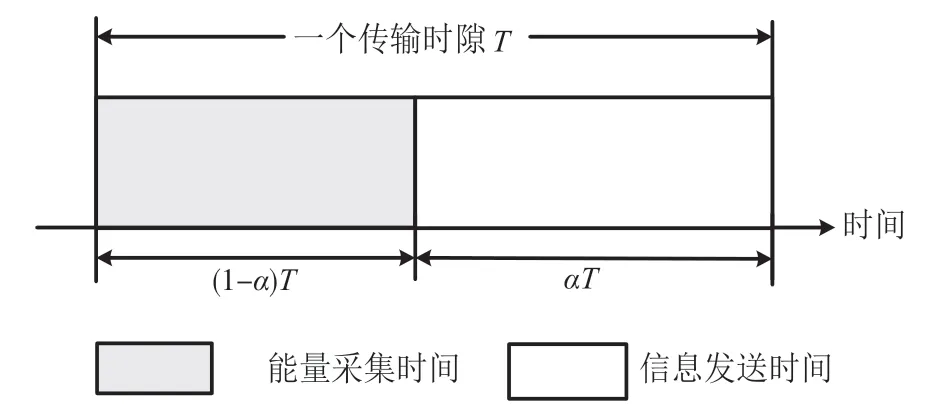
图1 时间分配示意图

因此，发送机接收到的信号可表示为：

1.3 通信行为检测

本文系统模型中，为隐藏发送机和接收机之间的通信行为，假设能量站、发送机和接收机三者协同工作。具体来说，接收机可以通过安全反馈链路获取估计信道状态信息（Channel State Information，CSI），但监听者不具有这样的反馈链路[9]，因此认为接收机可以消除能量站发送的干扰信号，同时监听者无法确定hbw信道的瞬时CSI。从保守角度考虑，假设监听者仍能获取hbw的统计CSI，且知晓htw的瞬时CSI。此外，能量站的发送功率Pb和时间分配因子α对于监听者也是已知的。

在上述假设情况下，通过分析监听者的检测性能来评价系统的通信隐蔽性，即监听者需要判断发送机与接收机间是否存在通信行为。因此，监听者面临一个二元检测问题。其中：零假设H0表示发送机没有发送任何信息；备择假设H1表示发送机向接收机发送信息。

监听者接收到的信号表示为：

2 隐蔽性能分析

分析监听者的检测性能，以评价系统的通信隐蔽性；推导接收机有效隐蔽传输速率，用于评价系统的通信质量。

2.1 隐蔽通信性能

根据Neyman-Pearson 准则[8]，监听者最小化其错判概率的方法是采用最大似然比检测（Likelihood Ratio Test，LRT）。根据文献[13]，在所考虑的系统下，在一个时隙中该检测可转化为监听者的平均接收功率，即可表示为：

式中：Tw表示监听者在一个时隙内的平均接收功率；τ表示监听者的检测门限。

Tw可以表示为：

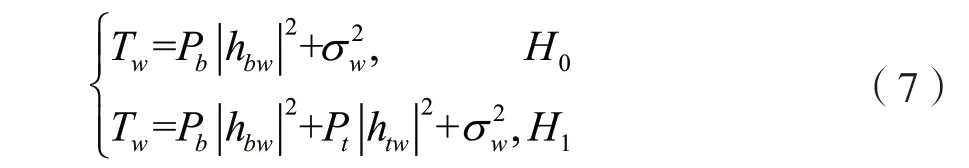
在H0和H1相等概率的情况下，监听者的二元假设检验性能可以由错判概率的加和进行评价，可以表示为：

式中：PFA=Pr(D1|H0)、PMD=Pr(D0|H1)分别表示虚警概率与漏检概率；D1和D0分别表示监听者做出发送机发送信息与否的二元判决。

引理1 虚警概率和漏检概率分别表示为：

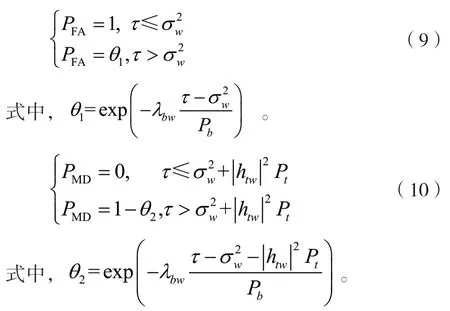
从保守的角度考虑，假设监听者采用最优检测门限以实现最小的错判概率加和。最优检测门限和最小错判概率可以由以下定理给出。

定理1监听者的最佳检测门限和相应的最小错判概率加和可以分别表示为：

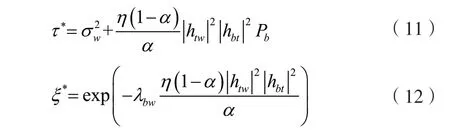
证明：

根据式（9）和式（10），错判概率可以被表示为：

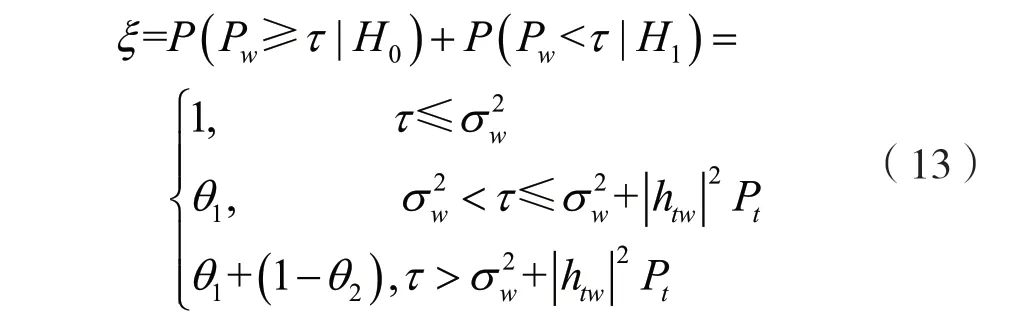
为确定最小错判概率的最佳检测门限，需要处理以下优化问题：

接下来将依次分析式（13）中的3 种情况。

综合上述情况，符合ξ*的最佳检测门限即τ*，定理1 得证。

直观地认为，增强能量站的发送功率可以增强通信隐蔽性，因为监听者接收到的干扰信号功率也随之增强。但是，根据式（12）发现，Pb对于ξ*无影响，意味着能量站的发送功率对通信隐蔽性无影响。这是因为增大能量站的发送功率不仅增大了监听者接收的干扰功率，也增大了发送机信息发送的功率，使得两者对于通信隐蔽性的影响相互抵消。同时，发现ξ*随着α的减少而增大，意味着分配更多的时间比例用于发送机的信息传输可以增强通信隐蔽性。因为发送机采用更小的信息发送功率，所以监听者更难以检测到通信 行为。

2.2 有效隐蔽传输速率

根据式（4）和φ=0 的情况（即完美干扰消除）[14]，接收机的信噪比（Signal-to-Noise Ratio，SNR）可以表示为：

本文假设发送机以固定速率发送信号至接收机，其中R0表示预设信息传输速率。由于htr的天然随机性，当R＜R0时，发送机的信息传输会发生中断，其中R=log2(1+γr)表示从发送机至接收机的可达信息传输速率。时间分配因子α也会影响发送机至接收机的可靠传输信息量，因此本文采用有效隐蔽传输速率这一性能指标来评价通信质量[15]，可以表示为：

式中，Pout=Pr(R＜R0)表示传输中断概率。

命题1有效隐蔽传输速率可以表示为：

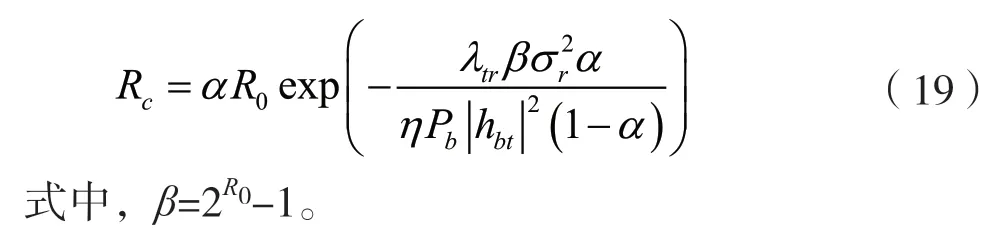
证明：

根据传输中断概率的定义，可以得出：

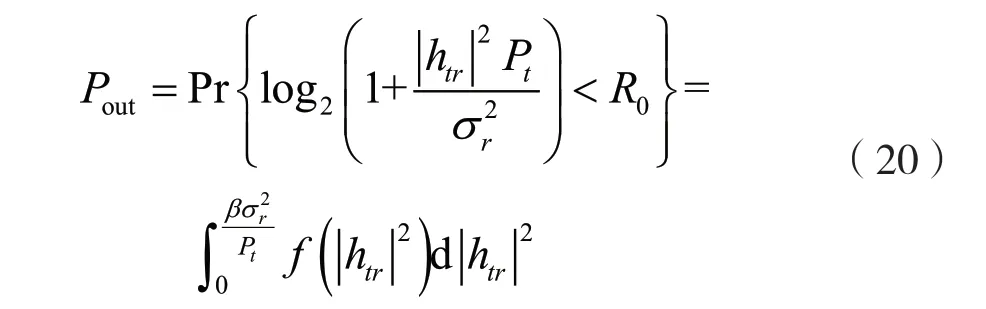
求解此积分，代入式（18）可得式（19）。根据式（20），可以发现Pout随着α增大而增大，这是因为发送机的发送功率较小导致的，进而导致通信质量下降。相对地，当α较小时，Rc也相对较小，这是因为可用于传输的时间较短，会导致通信质量下降。

3 隐蔽通信设计

根据式（11）和式（18）可以发现，在任意时隙中，时间分配因子会同时影响通信隐蔽性和通信质量。因此，下一步将通过优化α实现通信隐蔽性和通信质量性能间的折衷。具体来说，优化问题可以表示为：

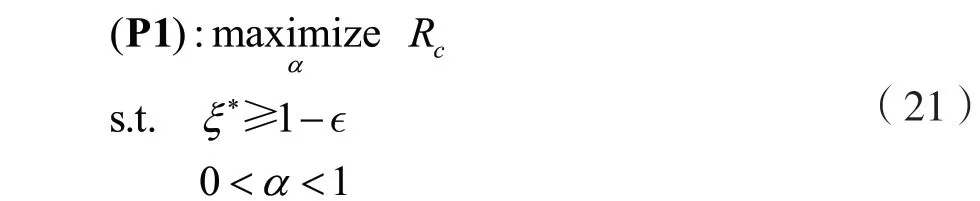
式中：约束条件ξ*≥1-є 是为了确保通信隐蔽性；≤01є≤表示隐蔽约束。优化问题（21）在接下来的定理求解。

定理2优化问题（21）的最优α可以表示为：

式中：

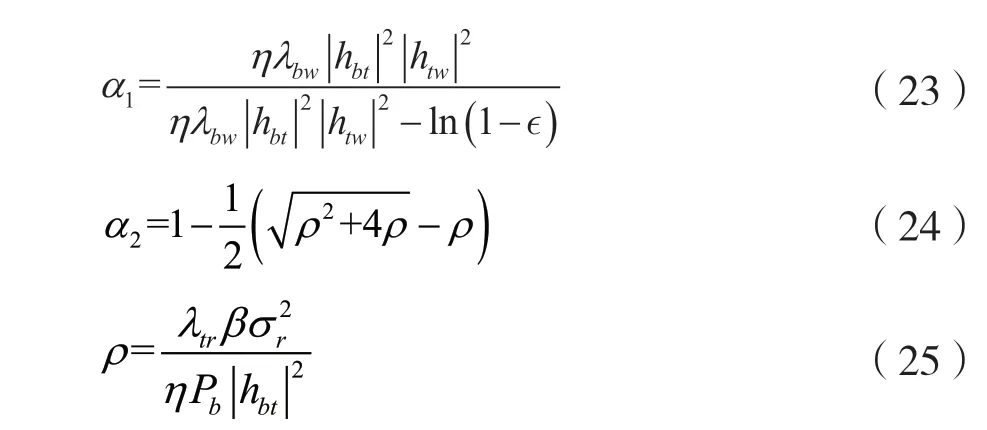
证明：首先，要确定ξ*关于α的单调性，相应的一阶导数可表示为：

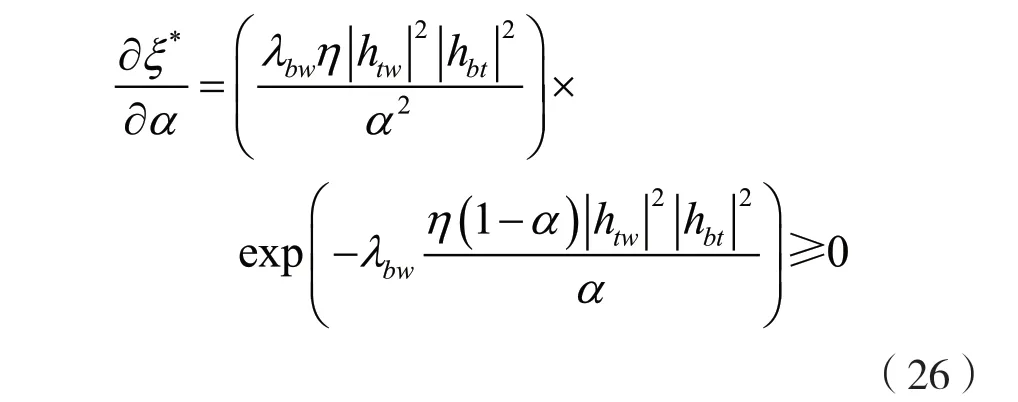
根据式（27）可知，ξ*是关于α的单调增函数。因此，约束条件ξ*≥1-є 导致α存在一个下界（即α≥α1），其中α1是等式（27）的解。

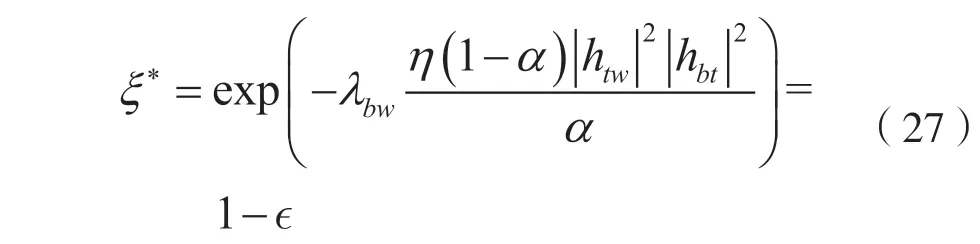
经过计算，α1的表达式由式（23）给出。接下来，优化问题（21）可以简化为：

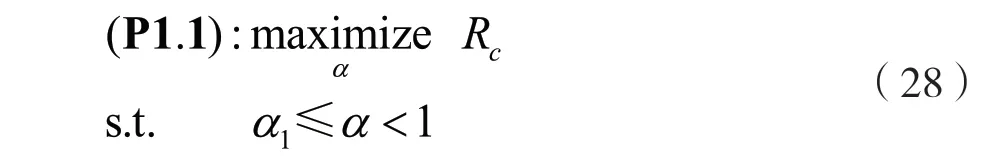
接下来，需要进一步分析Rc关于α的单调性。Rc关于α的一阶导数可以表示为：

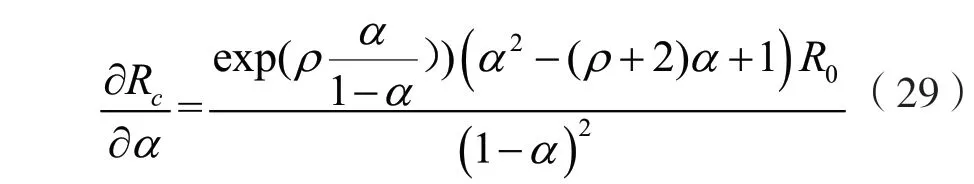
根据式（29），Rc关于α的单调性取决于α2-(ρ+2)α+1。根据一元二次方程的性质，α2-(ρ+2)α+1=0 的解可以表示为：

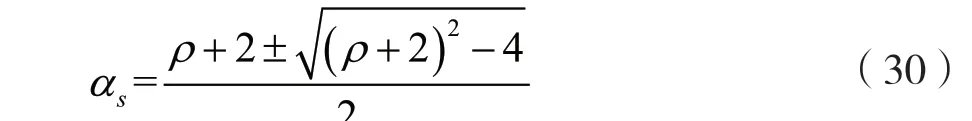
根据式（24），当Pb相对较大时，α2相对较小，因为需要确保发送机的能量供给。通常来说，α*取决于α1。根据式（23），α1随着є 的减少而增加。隐蔽约束越严格，在同一时隙中，发送机需要分配更多的时间用于信息传输。

4 仿真分析

为验证上述系统的性能进行仿真实验。仿真参数设置如下：接收机和监听者处的AWGN方差为所有信道增益的均值为λtr=λbw=|hbt|2=|htw|2=1，干扰消除系数为φ=0.001，能量站发送功率为Pb=30 dBm。

图2 给出了不同能量转化效率下最小错判概率随时间分配因子变化曲线。首先，ξ*随着α的增加不断增加。α逐渐增大表示发送机发送信息的时间变长，而(1-α)逐渐变小，收集能量时间变短而收集能量随之降低，导致发送功率较低，更易隐藏通信行为。因此，适当增加时间分配因子有助于提升通信隐蔽性。其次，最小错判概率随η增大而减小。η越大，表示发送机从能量站采集的能量更多地转换为自身能量，因而发送机发送信息的功率Pt也越大，此时更易暴露通信行为，导致隐蔽性能下降。

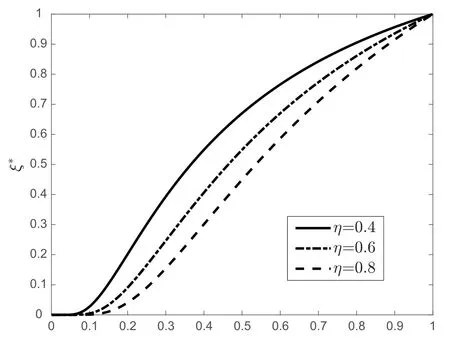
图2 不同能量转化效率下最小错判概率随时间分配 因子变化曲线

图3 给出不同隐蔽约束є 条件下，最佳时间分配因子α*关于预设传输速率R0关系。可见，随着R0的增长，α*先减小后不变。这是因为α的减小增加了信息发送的功率，导致传输中断概率的下降。然而，进一步降低α，导致有效隐蔽速率大幅度降低，尤其是当R0相对较大时。同时观察到，є越小，α*越大。这是因为更少的时间分配用于能量采集，可采用更低的信息发送功率，满足了隐蔽通信更严的隐蔽约束要求。

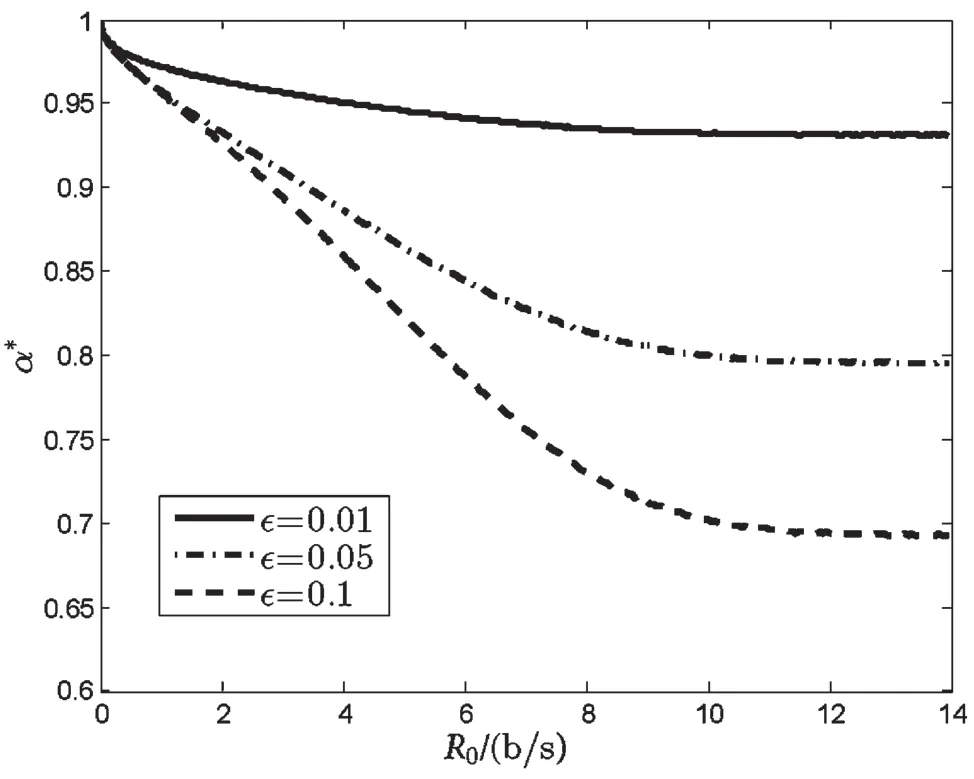
图3 不同隐蔽约束条件下最佳时间分配因子随传输 速率变化曲线

5 结语

本文研究了能量站辅助能量受限发送机的隐蔽通信。通过能量站发送的含有人工噪声的信号给发送机供能的同时迷惑监听者，利用信道不确定性，使合法通信方进行隐蔽通信。推导得出最小错判概率和时间分配因子的闭式表达式，以此达到通信隐蔽性和通信质量之间的折衷。结果表明，对于给定隐蔽约束条件，发送机与接收机可实现最佳隐蔽传输速率。