新的NOMA 多用户功率分配方法*

吴 霞，马文峰，王 聪，赵几航，曹 逊，姚远翔

（陆军工程大学，江苏 南京 210000）

0 引言

随着无线网络在各个领域的广泛运用，第5 代移动通信技术对频谱效率、数据速率、用户容量的要求不断提高。其中频谱效率需要提高5～15 倍，容量需要提高1 000 倍以上，4G 中广泛使用的正交多路访问技术（Orthogonal Multiple Access，OMA）逐渐无法满足需求。为了实现5G 的各种目标，学者们研究了多种相关技术。

文献[1-3]系统介绍了非正交多路访问（Non-Orthogonal Multiple Access，NOMA）技术的定义与优势，并引入功率复用的概念以达到提高频谱效率和系统容量的目标，另外NOMA 技术在提高接入用户数量上也有显著优势，能够满足未来的部署要求。文献[4]认为NOMA 可以提高频谱效率和小区边缘吞吐量，且具有低传输延迟、低信令成本以及能够实现海量连接等优点。文献[5]对NOMA 进行了分类，并针对不同类别NOMA 的功能进行了介绍和 比较。

NOMA 技术在发送端采用非正交发送，主动引入干扰信息，由多个用户共享同一个时频资源块，并根据用户的信道状况按照功率分配的方案进行功率分配。基站为信道状况差的用户分配更多发射功率，为信道状况好的用户分配较少的功率，以保证最大的功率差和最大用户容量，并达到区分不同用户的目的。接收端采用连续干扰消除技术，逐个对用户信号进行恢复。先恢复发射功率最大的用户信号；然后再恢复发射功率较小的用户信号，这是由于其他用户的发射功率较小，可以将其他用户造成的干扰直接视为噪声进行恢复；最后，再恢复次大功率的用户信号时减去最大功率的用户信号，以此类推完成所有用户信号的恢复。由此可见，NOMA技术是以接收机的复杂度来换取更高的频率谱效率，但随着芯片功能的不断提升，接收机的效能也会越来越强，这为NOMA 技术的不断成熟和广泛应用提供了更大的可能性。

目前不少学者对功率分配进行了研究并获得了一些可喜的成果。文献[6]是针对两个用户的NOMA 的研究，文献[7]是针对两个及两个以上用户的NOMA 的研究，两篇文章均考虑了最大化比例公平因子和最低的用户数据速率，但当小区边缘用户信道条件很差时，总体和速率却不如相同条件下的正交接入技术。文献[8]介绍了迭代注水法、固定功率分配法两种NOMA 功率分配方法，但没有考虑用户的（Quality of Service，QoS）这一约束条件。文献[9]提出了在总的发射功率一定和满足用户最小速率的条件下，最大化两个用户的和速率的方案，该方案虽然考虑了用户的QoS，但用户的总速率却低于OMA 技术。文献[10]提出了一种基于用户匹配与功率分配的NOMA 方案，在确保用户可靠性的前提下最大化用户容量，并采用查表的方式快速确定功率因子的选定。文献[11]提出了一种保护用户公平性的功率分配方案，在优化比例公平最差的用户的同时尽可能提高用户总的 速率。

本文基于用户的QoS，即在满足用户目标速率的情况下实现用户总容量的最大化，提出了新的NOMA 功率分配方案，尽可能提高用户总的可达速率，仿真结果表明提出方案的性能均高于同样条件下的OMA 方案的性能。

本文结构为：第1 节介绍系统模型；第2 节介绍本文的约束条件并介绍功率因子分配法；第3 节介绍逆注水算法和分数分配功率法；第4 节进行性能仿真分析；第5 节总结全文。

1 系统模型

在一个有n个(n≥2)用户的NOMA 用户配对组中，信道增益|h2|服从瑞利平稳衰落，即h～CN(0,λ)。其中λ=d-v，v 为路径损耗指数。将用户按照距离基站的远近进行排序，即d1＜d2＜d3＜…＜dn，则对应的信道增益排序为|h1|2＞ |h2|2＞|h3|2＞…＞|hn|2。基站总的发射功率为Ptotal。按照NOMA 的功率分配原则：给信道增益最大的用户信号分配最少的发射功率；给信道增益最小的用户信号分配最多的发射功率。基站给各个用户分配的功率因子应满足α1＜α2＜α3＜…＜αn，即发射功率应满足P1＜P2＜P3＜…＜Pn。其中功率因子与发射功率之间的关系为：

在接收端，接收机利用（Successive Interference Cancellation，SIC）优先恢复功率最大的用户信号，将剩余用户信号直接作为干扰噪声，在恢复次大功率信号时减去已恢复的用户信号并将剩余的用户信号作为干扰噪声，以此类推恢复所有用户 信号。

本文考虑由用户1、用户2、用户3 这3 个配对用户组成的基本NOMA 模型，如图1 所示。3 个用户距离基站的距离由近至远，即d1＜d2＜d3，则信道增益满足|h1|2＞|h2|2＞|h3|2。按照NOMA 的功率分配原则分配给3 个用户的功率分别为P1、P2、P3，则P1+P2+P3=Ptotal，相应的功率分配的功率因子α1＜α2＜α3，则P1=α1Ptotal，P2=α2Ptotal，P3=α3Ptotal，P1＜P2＜P3，其中α1+α2+α3=1。

图1 系统模型

2 约束条件和功率因子分配方案

2.1 用户各自的容量

本文以各个用户成功由SIC 恢复信号后的可达数据速率代表该用户的容量，则用户1、用户2、用户3 的容量分别为式（1）、式（2）、式（3）。

式中：N0为高斯白噪声的方差。

2.2 配对用户组的总容量

由用户1、用户2、用户3 配对的用户组的总容量为：

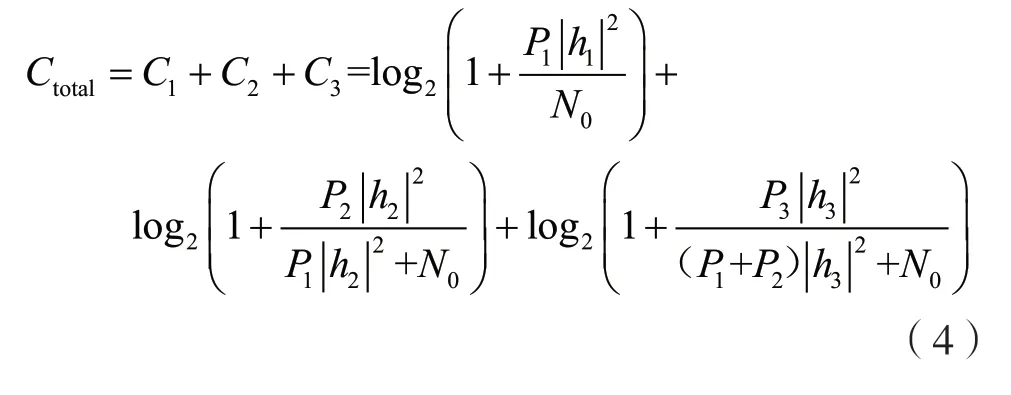
2.3 功率因子分配方案

根据功率因子的两个约束条件：α1＜α2＜α3，α1+α2+α3=1。

本文的优化方案是将功率因子α2假设为变量α，功率因子α1假设为α2，则功率因子α3=1-α-α2。结合上述约束条件可得变量α的取值范围为将P1=α1Ptotal，P2=α2Ptotal，P3=α3Ptotal代回式（4）中可得：

另外，信道增益最好的用户分配到的发射功率存在上限。接收端采用SIC 技术对用户信号进行解调时，用户之间需要存在功率间隔ΔP，这最终将推导出信道增益最好的用户分配到发射功率的最大值。在有n（n≥2）个用户共享资源的信道上，功率间隔ΔP满足：

2.4 接收端方案

图2 接收端SIC 解调方案

2.5 信道增益|h2|对用户总容量的影响

根据目前的研究表明，用户的信道增益与用户距离基站的距离直接相关。用户距离基站越近，信道条件越好，即信道增益越大，所以在本文中选择用户与基站之间的距离d作为表征信道增益|h2|大小的影响因素。本文中信道增益|h2|服从瑞利平稳衰落，即h～CN(0,λ)，其中λ=d-v，v为路径损耗指数。

如图3 所示，对于用户1，固定d2=0.7，d3=1.0，选择功率因子α=0.41，d1从0.1 增大到0.5。随着d1逐渐增大，用户1 的信道增益|h12|逐渐减小。由式（1）可知，用户1 的容量逐渐减小，则用户总容量逐渐减小；信噪比SNR的公式为随着信噪比SNR 的增大，即N0减小，由式（1）、式（2）、式（3）可知，各个用户的容量分别在增大，则总容量增大。

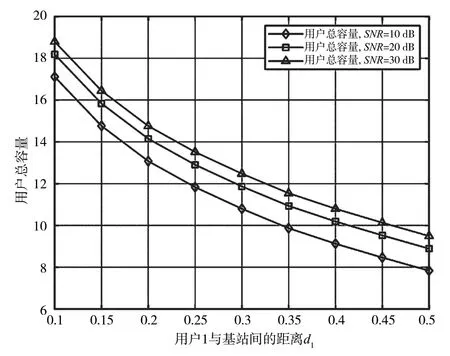
图3 随信噪比增大，用户总容量与d1 的关系

2.6 功率因子α 对用户总容量的影响

2.6.1 用户与基站间距离不变

如图4 所示，在信噪比SNR=10 dB 时，假设用户距离基站的距离d1、d2、d3固定，式（1）用α表示，并对C1关于α求导可得：

由于α为正，可见C1'始终为正，C1随α增大单调递增，即随着功率因子α的增加（用户1 的功率因子α1=α2也增加），用户1 的容量不断增加，如图4（b）中叉型线所示。

同理对公式（2）关于α求导可得：

用户总容量的变化趋势如图4（a）中所示，随着功率因子α的增大不断增大。

图4 信噪比和距离一定时，用户容量随功率因子的变化曲线

2.6.2 用户与基站间距离改变

本节研究在某一用户距离基站的距离变化时，功率因子对用户总容量的影响。

信噪比固定在10 dB，d2=0.6，d3=0.9，d1从0.1逐渐增加到0.5。如图5 所示，随着d1的不断增大，用户总容量不断减小，这是由于随着用户1 距离基站的距离逐渐变远，用户1 的信道增益|h12|逐渐减小。由式（1）可知，该用户自身的容量不断减小，则总容量也不断减小；但随着功率因子的不断增大，用户总容量是不断增大的。

图5 d1 逐渐增大时，用户总容量随功率因子的变化曲线

若用户2、用户3 与基站间的距离变化，由1.5节中的结论可得：随着d2、d3的不断增大，用户总容量不断减小；但随着功率因子的不断增大，用户总容量是不断增大的。

2.7 信噪比SNR 对用户总容量的影响

固定d2=0.6、d3=0.9，由1.5 节中结论可知，d1从0.1 逐渐增加到0.5，用户总容量减小。SNR的公式为考虑ps从5 dB 增大到10 dB，即N0从减小到从式（1）、式（2）、式（3）可以看出，随着N0的减小，各个用户的容量在增加，代入式（4），可以得出用户总容量也在增加。仿真结果如图6 所示，随着SNR的逐渐增大，用户总容量不断增大。

图6 d1 逐渐增大时，用户总容量随信噪比SNR 的变化

由1.5 节中结论可知，当d2、d3逐渐增大，随着N0的减小，SNR逐渐增大，各个用户的容量增加，用户总容量也增加。

3 逆注水算法和分数方法分配发射功率

3.1 逆注水算法

注水算法是根据某种准则并根据信道状况对发射功率进行自适应分配。该算法通常是给信道状况好的多分配功率，给信道状况差的少分配功率，从而达到传输速率的最大化；而NOMA 的功率分配思想是为信道状况好的少分配功率，为信道差的多分配功率。本文利用注水算法的思想，先将发射功率分配成3 份，再根据NOMA 的功率分配思路，实现逆注水算法，即将分出的3 份功率中最大的一份功率分配给信道最差的用户信号，将最小的一份功率分配给信道最好的用户信号。

在d1=0.3、d2=0.6、d3=0.9，总功率假设为1 时，利用逆注水算法得到各个用户的信道增益、分配到的发射功率、用户容量以及用户总容量如表1 所示，由各个用户的容量情况可知满足本文所考虑的QoS。

表1 逆注水算法结果

3.2 分数方法

分数方法是基于用户信道状态信息进行发射功率自适应分配的算法。由于本文中信道状态信息以信道增益的大小来标识，信道增益的大小由用户距离基站的距离来决定，算法中设置一个衰减因子μ(0 ＜μ＜1)：

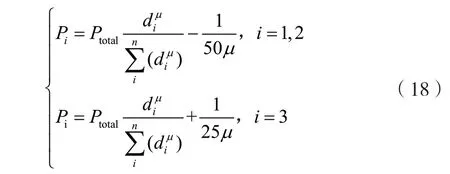
根据式（18）进行发射功率的分配，然后得到各个用户的容量与总容量。

将衰减因子μ从0.01 起以0.01 的步长增长到1，观察每次分配的功率结果。发现随着衰减因子的增加，信道状态好的用户分配到的发射功率逐渐减小，信道状态越差的用户分配到的发射功率越来越大；相应的信道状态好的用户容量逐渐减小，信道状态越差的用户容量逐渐增大，但总容量逐渐减小。结合约束条件中信道增益最大的用户信号可分得的发射功率不大于此处n=3，Ptotal=1，即本文目标是最大化用户总容量，则选取P1最接近且略小于0.25 时的衰减因子，同时考虑用户的QoS，即检验此时各个用户的可达速率是否大于等于目标速率，可得到使用分数分配算法可获得的最大用户总容量。

4 仿真结果

本文通过MATLAB 软件对提出的功率分配方案进行测试仿真，信道条件选择瑞利衰落信道。在用户与基站距离、总的发射功率均归一化为1 的条件下，考虑相同最低目标速率功率因子信道增益最大的用户信号所分得的发射功率小于等于0.25。

4.1 选择距离基站最远的用户3 进行匹配

已知两个距离基站d1=0.1，d2=0.4 的用户1、用户2，另外选择一个用户3 进行配对。在同一时频资源上进行功率复用，按照本文所给的3 种功率方案进行功率分配以得到最大用户总容量，并与现有的OMA 方案进行比较。

4.1.1 d3 不同的情况下，功率因子对用户总容量的影响

根据距离由近至远的原则，用户3 距离基站的距离d3从0.5 取至1.0。随着功率因子的增大，用户总容量也在不断增大；随着用户3 距离基站的距离增大，用户总容量在逐渐降低。由此可见，应当选取距离基站最近的用户，如用户3 与用户1、用户2 进行配对并复用发射功率，可以使得用户总容量达到最大值。除此之外，由于功率因子的取值受到约束条件的限制，最终确定的功率分配方案中的功率因子应当选择满足约束条件的功率因子的最大值。如图7 所示，选取d3=0.5 时的用户3，相应的功率因子α的取值被约束条件限制在（0.008 0,0.354 4），则当α=0.354 4 时，用户总容量取得最大值，为13.757 2。

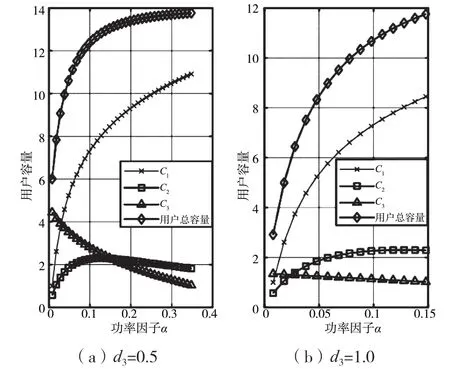
图7 不同d3 时，随功率因子α 变化的用户容量

4.1.2 d3 不同的情况下，逆注水算法对用户总容量的影响

根据逆注水算法，与1 中在同一环境中进行功率分配。由于用户3 距离基站距离最远，它分得的发射功率最大，用户1 分得的发射功率最小；随着用户3距离基站越来越远，用户总容量也在逐渐下降。如图8 所示，当用户3 距离基站的距离d3=0.5 时，用户的总容量最大，达到21.711 2，由此可见，逆注水算法在最大化用户容量方面是优于功率因子分配方案的。

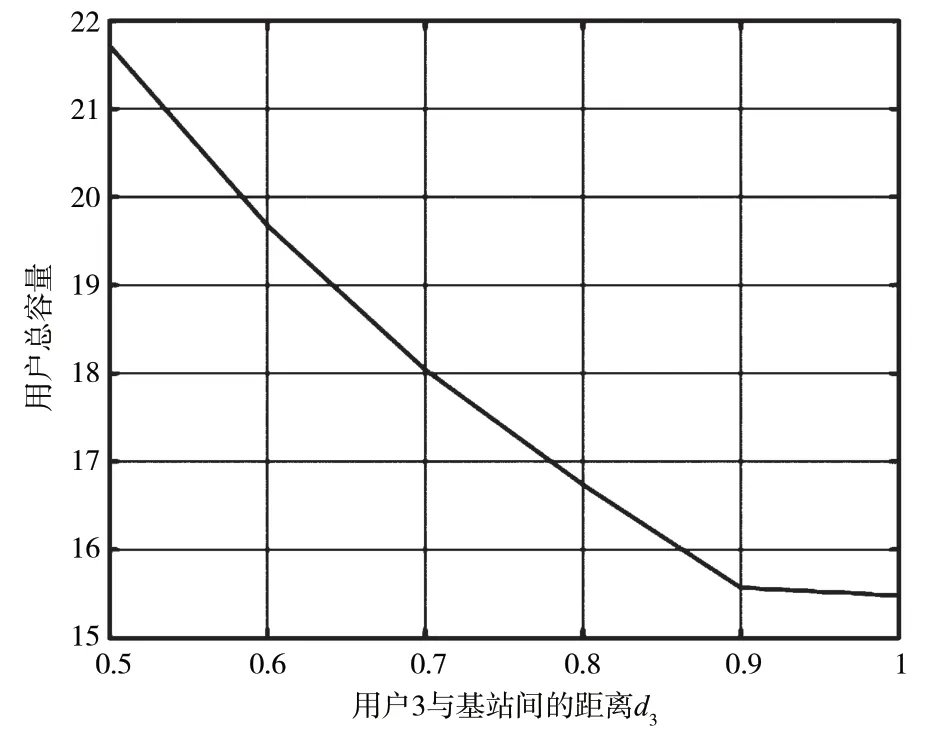
图8 不同d3 时，逆注水算法用户总容量

4.1.3 d3 不同的情况下，分数分配法对用户总容量的影响

利用分数分配法进行功率分配，此时n=3。根据前文分析，选取P1最接近且略小于0.25 时的衰减因子可得到使用分数分配算法可获得的最大用户总容量。由仿真结果可得，如图9 所示，随着d3逐渐增大，用户总容量逐渐减小，所以取d3=0.5 时的用户3 与用户1、用户2 进行配对。由仿真结果可知此时各个用户的可达速率是大于目标速率的，满足用户的QoS，因此可得最大用户容量13.811 1。由此可见，分数分配法在最大化用户容量方面优于第1 种方案，但不如逆注水算法。

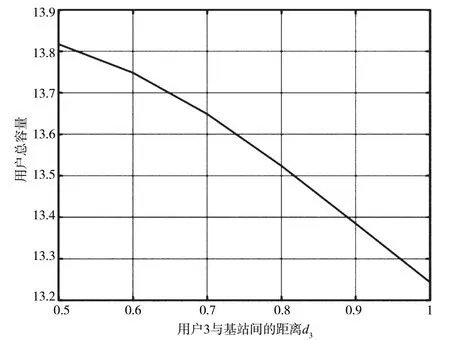
图9 不同d3 时，分数分配法用户总容量

4.1.4 d3 不同的情况下，OMA 方案对用户总容量的影响

OMA 方案中，各用户的容量为：

此外α1=α2，α2=α，α3=1-α-α2。可得随着功率因子的逐渐增大，用户总容量也逐渐增大；随着用户3 距离基站越来越远，用户总容量逐渐减小。如图10 所示，可知当功率因子α≈0.41 时，选取d3=0.5 的用户3 与用户1、用户2 进行配对可以得到最大用户总容量6.782 6。由此可见，OMA 方案比上面3 种方案的效果都要差一些，这也证明了NOMA 的优越性。

图10 OMA 方案在不同d3 随功率因子变化用户总量的变化

如图11 所示，可知同样的条件下，4 种分配方案随着用户3 距离基站的距离增大可得的用户总容量大小。

图11 不同d3 时四种分配方案下用户总容量

由大到小依次为逆注水算法、分数分配功率算法、功率因子分配法、OMA 方案。前3 种均属于NOMA 方案，且数值上均远大于OMA 方案，由此可见，在最大化用户总容量方面，NOMA 方案是远远优于OMA 方案的。

4.2 选择距离基站最近的用户1 进行匹配

已知两个距离基站d2=0.6，d3=0.9 的用户2、用户3，另外选择一个用户1 进行配对。在同一时频资源上进行功率复用，按照本文所给的3 种功率方案进行功率分配以得到最大用户总容量，并与现有的OMA 方案进行比较。

4.2.1 d1 不同的情况下，功率因子对用户总容量的影响

根据距离由近至远的原则，用户1 距离基站的距离d1从0.1 取至0.5。随着功率因子的增大，用户总容量也在不断增大；随着用户1 距离基站距离的增大，用户总容量在逐渐降低。由此可见，应当选取距离基站最近的用户1 与用户2、用户3 进行配对并复用发射功率，可以使得用户总容量达到最大值。除此之外，由于功率因子的取值受到约束条件的限制，最终确定的功率分配方案中的功率因子应当选择满足约束条件的功率因子的最大值。如图12 所示，选取d1=0.1 时的用户1，相应的功率因子α的取值被约束条件限制在（0.007 9,0.237 3），则当α=0.237 3 时，用户总容量取得最大值，为12.277 1。

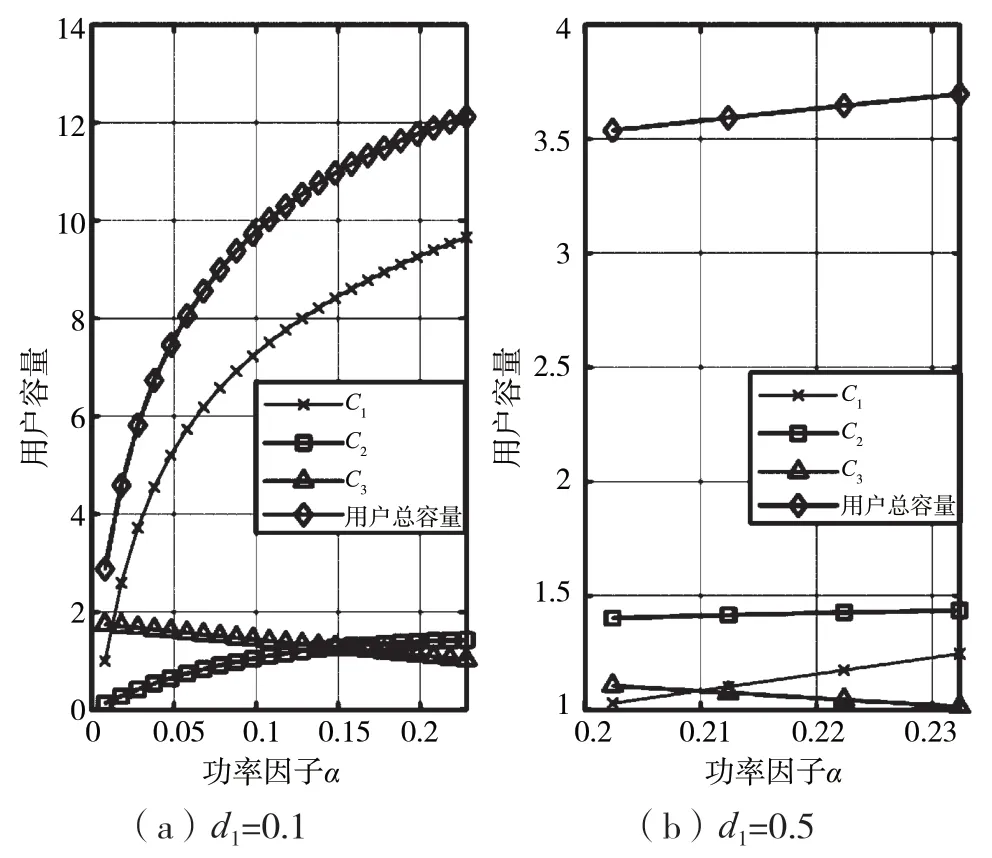
图12 不同d1 随功率因子变化的用户容量

4.2.2 d1 不同的情况下，逆注水算法对用户总容量的影响

根据逆注水算法，与3.2.1 在同一环境中进行功率分配。由于用户1 距离基站距离最近，它分得的发射功率最小，用户3 分得的发射功率最大，随着用户1 距离基站越来越远，用户总容量也在逐渐下降。如图13所示，当用户1距离基站的距离d1=0.1时，用户的总容量最大，达到15.206 8。由此可见，逆注水算法在最大化用户容量方面是优于第1种方案的。

图13 不同d1 时逆注水算法用户总容量

4.2.3 d1 不同的情况下，分数分配法对用户总容量的影响

利用分数分配法进行功率分配，此时n=3。由前文分析，选取P1最接近且略小于0.25 时的衰减因子可得到使用分数分配算法可获得的最大用户总容量。根据仿真结果可得，如图14 所示，随着d1逐渐增大，用户总容量逐渐减小，所以取d1=0.1 时的用户1 与用户2、用户3 进行配对，此时各个用户的可达速率均大于目标速率，满足用户的QoS，可得最大用户容量12.476 7。由此可见，分数分配法在最大化用户容量方面是优于第1 种方案，但不如逆注水算法。

图14 分数分配法用户总容量

4.2.4 d1 不同的情况下，OMA 方案对用户总容量的影响

OMA 方案中，由3.1 节中公式得出的总容量随着功率因子的逐渐增大而增大；随着用户1 距离基站越来越远而减小。如图15 所示，所以可知当功率因子α≈0.41 时，选取d1=0.1 的用户1 与用户2、用户3 进行配对可以得到最大用户总容量4.602 3。由此可见，与3.1 节得出了相同的结论，也证明了NOMA的优越性。

图15 OMA 方案在不同d1 随功率因子变化用户总量的变化

将4 种分配方案进行比较，结果如图16 所示，在同样的条件下，随着用户1 距离基站的距离增大可得的用户总容量大小，由大到小依次为逆注水算法、分数分配功率算法、功率因子分配法、OMA 方案，这与3.1 中得到的结果也是一致的。进一步验证了在最大化用户总容量方面，NOMA 方案是远远优于OMA 方案的。

图16 不同d1 时4 种分配方案下用户总容量

由于文献[10]中的算法是基于2 个用户配对进行功率分配所提出的，此处将本文提出的逆注水算法、分数分配法用于2 个用户配对的情况并与文献[10]中的算法进行比较。固定用户1，随着用户2 的距离d2逐渐增大时，由文献[10]可知，当功率因子α从0.49 逐渐减小时，用户总容量逐渐减小，且随着用户2 的距离d2逐渐增大，用户总容量也逐渐减小，即当功率因子α取0.49、用户2 的距离d2取0.6 时，可得最大用户容量11.509 1。在同等条件下的逆注水算法和分数分配法可得的用户总容量为11.509 3、11.508 6，此时3 种方法中最优的是逆注水算法，其次是文献[10]中的算法，最后是分数分配法。当功率因子小于0.49 时，逆注水算法和分数分配法都优于文献[10]中的算法，具体仿真结果如图17 所示。

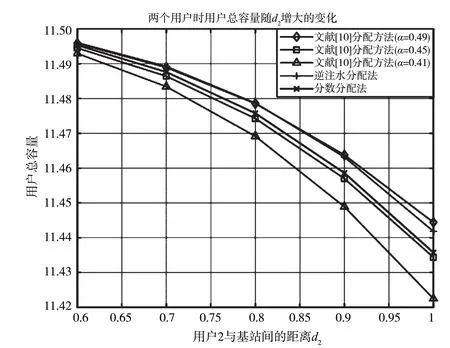
图17 逆注水算法、分数分配法与文献[10]算法比较结果

5 结语

本文提出了3 种NOMA 的功率分配方案，分别是功率因子分配法、逆注水算法、分数分配法。在NOMA 场景下，3 个用户进行功率复用，对于信道条件差、增益小的用户信号分配更多的发射功率；对于信道条件好、增益大的用户信号分配较少的发射功率。在满足最低用户目标速率这一用户QoS，以及信道条件最好的用户可分得最大发射功率的情况下，尽可能提高用户的可达速率，即最大化用户容量。仿真结果表明，功率因子分配法、分数分配法、逆注水算法3种方案的用户总容量是递增的，再与OMA 的功率分配方案相比，即使是以上3 种中最差的功率因子分配方案的结果也优于OMA 的功率分配方案。