“二、一组合”图象如何选

刘家良

在同一坐标系内选择正确的二次函数与一次函数组合图象，是中考数学中一类常见问题.那么这种“二、一组合”图象应如何选呢？下面举例介绍.

一、看同一个字母常数的取值范围

先由两个函数的图象分别确定其中字母常数的取值范围，再看同一个字母常数的取值范围是否相同，若相同，则说明两图象的组合是有可能的.

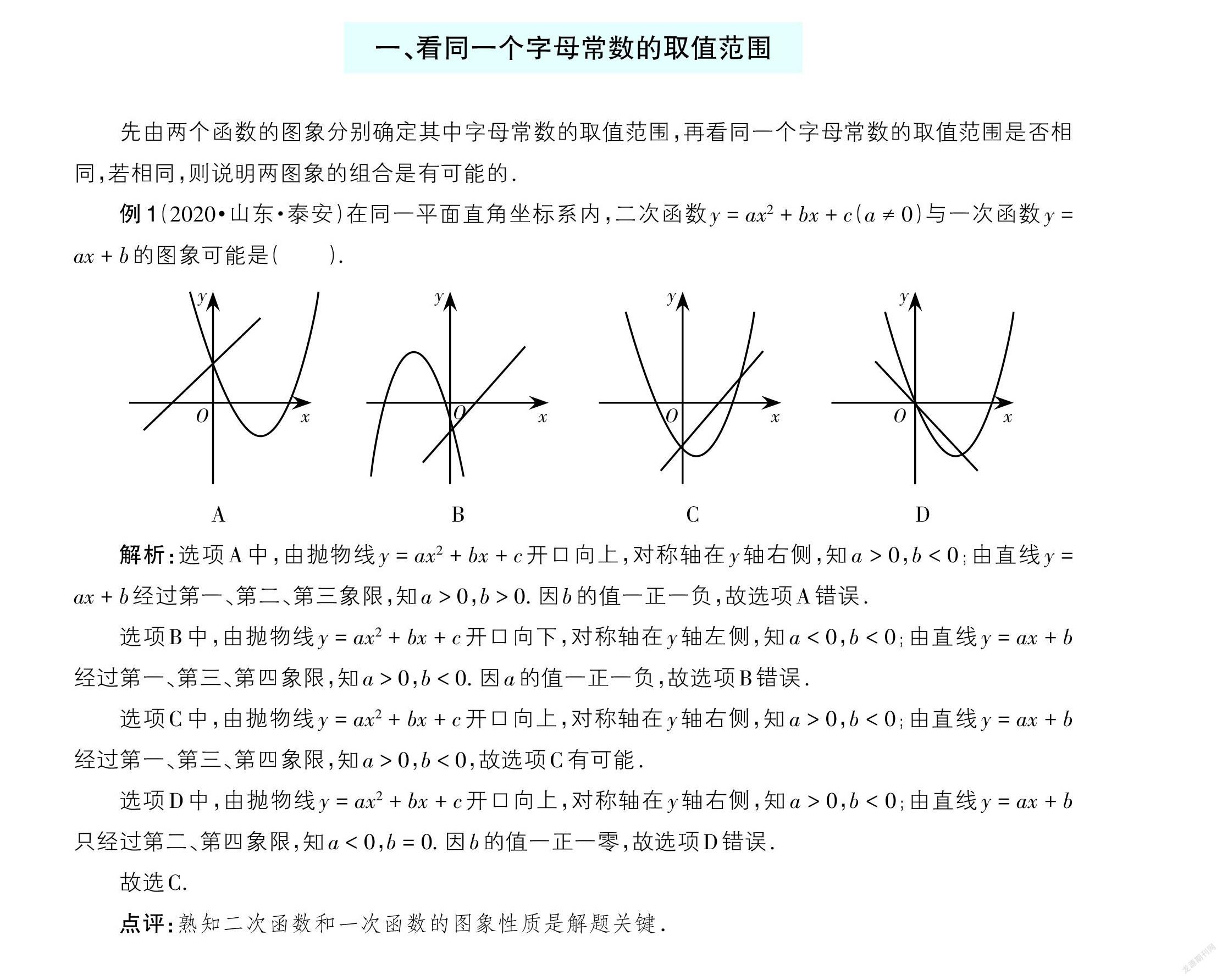
例1（2020·山东·泰安）在同一平面直角坐标系内，二次函数y = ax2 + bx + c（a ≠ 0）与一次函数y = ax + b的图象可能是（ ）.

解析：选项A中，由抛物线y = ax2 + bx + c开口向上，对称轴在y轴右侧，知a > 0，b < 0;由直线y = ax + b经过第一、第二、第三象限，知a > 0，b > 0. 因b的值一正一负，故选项A错误.

选项B中，由抛物线y = ax2 + bx + c开口向下，对称轴在y轴左侧，知a < 0，b < 0;由直線y = ax + b经过第一、第三、第四象限，知a > 0，b < 0. 因a的值一正一负，故选项B错误.

选项C中，由抛物线y = ax2 + bx + c开口向上，对称轴在y轴右侧，知a > 0，b < 0;由直线y = ax + b经过第一、第三、第四象限，知a > 0，b < 0，故选项C有可能.

选项D中，由抛物线y = ax2 + bx + c开口向上，对称轴在y轴右侧，知a > 0，b < 0;由直线y = ax + b只经过第二、第四象限，知a < 0，b = 0. 因b的值一正一零，故选项D错误.

故选C.

点评：熟知二次函数和一次函数的图象性质是解题关键.

例2（2020·山东·菏泽）一次函数y = acx + b与二次函数y = ax2 + bx + c在同一平面直角坐标系中的图象可能是（ ）.

解析：选项A中，由抛物线y = ax2+bx+c的图象，知a > 0，b < 0;由直线y = acx + b与y轴正半轴相交，知b > 0. 因b的值一正一负，故选项A错误.

选项B中，由抛物线y = ax2+bx+c的图象，知a > 0，b > 0，c > 0，于是ac > 0;由直线y = acx + b经过第一、第二、第三象限，知ac > 0，b > 0. 故选项B有可能.

选项C中，由抛物线y = ax2+bx+c的图象，知a < 0，b > 0;由直线y = acx + b与y轴负半轴相交，知b < 0. 因b的值一正一负，故选项C错误.

选项D中，由抛物线y = ax2+bx+c的图象，知a < 0，b < 0;由直线y = acx + b与y轴正半轴相交，知b > 0. 因b的值一正一负，故选项D错误.

故选B.

点评：例2与例1的解题思路都是先由图象特征确定字母常数的取值范围，再看同一个字母常数的取值范围是否相等，例2与例1的不同点是一次函数y = acx + b中一次项的系数是ac，是两个字母常数的积，此处要有整体意识.

二、图象与常数的互化

例3（2020·四川·达州）如图，直线y1 = kx与抛物线y2 = ax2 + bx + c交于A，B两点，则y = ax2 + （b - k）x + c的图象可能是（ ）.

解析：由直线y1 = kx与抛物线y2 = ax2 + bx + c的图象，知k > 0，a < 0，b < 0，c < 0，于是b - k < 0，[-b-k2a] < 0. 由直线y1 = kx与抛物线y2 = ax2 + bx + c交于A，B两点，知关于x的一元二次方程kx = ax2 + bx + c即ax2 + （b - k）x + c = 0有两个不相等的实数根，相应地，y =  ax2 + （b - k）x + c与x轴有两个交点. 又因为a < 0，所以y =  ax2 + （b - k）x + c的图象开口向下，对称轴在y轴的左侧.

故选B.

点评：由图象到常数，再由常数到图象，这一正、逆过程体现了数形结合与转化的思想.