截面积尺寸对微通道换热器流动特性的影响机理

高 博， 焦永刚， 田玉思， 孙会凯

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

微通道作为微元器件中的重要部件，具有尺寸小、质量轻、响应快、精度高、性能好和成本低等特点，广泛应用于各种流动的控制元件中，用以实现微混合、微分离、微冷凝、微检测等功能[1-3]。目前很多学者展开微通道截面形状对微尺度流动及换热特性影响的研究。Xu et al[4]采用不同的实验测量方法研究了不同宽高比微通道的流动特性，结果表明微通道中的流动与传统的N-S方程符合很好。刘赵淼等[5]对不同水力直径、截面宽高比和通道长度的矩形微通道的流动和传热性能进行了数值模拟研究，指出矩形微通道的几何尺寸对流动泊肃叶数(Po)和努赛尔数(Nu)的影响。鲁进利等[6]分别对截面形状为三角形、矩形、半圆形的微通道进行了数值分析和实验研究，所研究微通道当量直径为0.210～1.069 mm，雷诺数Re为102～104,结果表明,当截面形状相同时，摩擦阻力系数随着当量直径的减小而降低。王二利等[7]以去离子水和质量分数为0.3%的水基纳米流体为工质，对水力直径为1.241 mm的矩形微通道内两相流流动压降进行实验研究,结果表明，质量流速和热流密度的增大均会提高流动压降。Paisarn et al[8]对不同宽高比的微小矩形通道流动换热进行了研究，实验表明，宽高比对微小通道和流动换热有着显著的影响，相同雷诺数下，宽高比越大，则通道进出口压降越小。程炜等[9]以去离子水为工质，对高2 mm，宽分别为0.3、0.6、2 mm的矩形微槽道中的两相传热和流动阻力特性进行实验研究，结果表明，矩形槽道压降随着尺寸的减小而增大。Zhang et al[10]对水在不同宽高比矩形微小通道组内流动换热特性进行了实验研究，宽高比范围在0.45～0.88之间，雷诺数范围在 120～3 750 之间，结果表明，转捩雷诺数提前，摩擦力和入口效应的影响不可忽略。江乐新等[11]对3组不同水力直径的矩形微通道内流体的流动特性开展数值模拟研究，获得水力直径对流动特性的影响规律，研究结果表明水力直径越小，临界Re值越小。高超等[12]研究了不同宽高比矩形金属微尺度通道的流动特性，金属微尺度通道宽为0.4 mm，通道宽高比分别为0.5、0.67、1 mm，实验结果表明微尺度矩形通道摩擦因数随着雷诺数增大而减小，在转捩区出现明显增大后再减小。Pfund et al[13]测量了水流过水力直径为200～900 μm的矩形微槽道时的压降，发现水力直径越小，压降越大。

国内外学者对微细尺度结构内部流动机理已进行了大量的研究，并对微尺度热交换器对流换热能力的强化等工作进行了深入研究，取得很大的进展。但是关于微尺度热交换器截面积尺寸变化对流量分配均匀性的影响研究相对较少，文中提到的截面积尺寸包括微通道的通道当量直径、通道的高宽比和通道数(通道面积与联箱的关系)。现以平行通道换热器为研究对象，通过数值模拟的方式研究了微通道截面积尺寸变化对流体分配均匀性和压降特性的影响。

1 物理模型

换热器截面积尺寸如图1所示。

图1 微通道换热器示意图

整个换热器厚度为5 mm，进出口联箱厚度2 mm，联箱长宽都为20 mm；通道长40 mm，中心距1 mm，其中，W1为通道宽，W2为中心距，H1为玻璃盖板厚度，H2为通道高度，H3为通道底部到铜板底部距离。通道高宽呈有规律性变化，但中心距不变，进出口位置均位于铜板下侧，且都是从铜板下面的进口垂直进入联箱后进入各个通道，然后经出口联箱再流出微通道换热器。

2 数学模型

2.1 假设条件

为简化问题，对模型做以下假设：

(1)流体流动过程是稳态的；

(2)流体为单相理想不可压缩流体，流动为紊流；

(3)忽略流体重力作用及流体的黏度耗散；

(4)无滑移边界条件。

2.2 控制方程

对于通道内的液体三维流动，其控制方程包括连续性方程和N-S方程。

(1)连续性方程

(1)

(2)动量方程

(2)

(3)

(4)

式中，ρ为流体密度；p为压力；μ为流体动力黏度；u、v、w分别为速度在x、y、z方向上的速度分量。

2.3 网格独立性验证

为保证计算精度，对换热器网格独立性进行了验证。以高宽为0.5 mm×0.2 mm的Z型换热器(如图1所示，通道进出口位于进出口联箱两侧)为例，进口速度0.2 m/s，网格间距分别为0.4(33 040个)、0.3(74 150个)、0.2(250 520个)、0.1(1 986 740个)时进行数值模拟，并且对通道内网格进行了加密处理，模拟结果如图2所示。

图2 网格数量与压降的关系

由图2可以看出，当网格数从250 520个增至1 986 740个时，计算出的压降基本不变。综合计算精度及计算时间考虑，本文采用网格数为250 520(网格间距为0.2)的模型进行模拟计算较为合理。

2.4 模型可靠性验证

(5)

式中，ρ为标准大气压及室温下的水密度，取998.2 kg/m3；v为各种阻力下对应的速度分布，v=Q/A，Q为通道的体积流量，A为通道的流通面积;l为直通道长度；d为直通道的当量直径。

图3为不同雷诺数下摩擦系数理论计算值和模拟值的比较。由图3可以看出，随着雷诺数的增大，两者的误差略有增加，在雷诺数为9 512时，最大误差为10.8%。表1列出了高宽为0.5 mm×0.2 mm的Z型换热器在雷诺数为9 512时的进出口压降理论计算值，模拟值为3 273 203 Pa，理论计算值与模拟值的相对误差为7%，数值模型可靠。

图3 理论计算值和模拟值的比较

表1 进出口压降理论计算值 Pa

3 结果与分析

为了分析换热器的流量分配均匀性，采用标准差估计换热器整体和各通道的流量分配情况，标准差能反映随机变量在数学期望值周围的波动程度，其大小与波动程度一一对应。定义各通道流量分配不均匀度为无量纲数E，如式(6)所示，定义总流量分配不均匀度为无量纲数S，如式(7)所示。其中E和S值越小，表明流量分配均匀性越好。

(6)

(7)

式中，Mi、Ma分别为第i根微通道内流体流量和微通道内流体的平均流量；n为该微通道的通道个数。

3.1 通道当量直径对流动特性的影响

为了优化换热器的换热能力，针对不同当量直径微通道内流动特性进行了研究，保证通道面积大小为1 mm2，当量直径分别为0.19、0.21、0.23、0.26、0.28、0.30、0.31 mm。

(1)流量分配均匀性。用标准差评估各类型换热器的总流量分配情况，S值越小，说明该类型换热器流量分配均匀性越好；反之，流量分配均匀性越差。图4所示为入口速度0.10、0.15、0.20 m/s时，不同类型换热器总流量分配均匀度，试验件的通道面积不变，当量直径改变。由图4可以看出，当量直径小于0.23 mm时，总流量分配不均匀度随当量直径的增大逐渐减小；当量直径大于0.23 mm小于0.26 mm时，总流量分配不均匀度随当量直径的增大逐渐增大；当量直径大于0.26 mm时，总流量分配不均匀度随当量直径的增大逐渐减小。通道面积相同的矩形和正方形通道相比，正方形通道对应的当量直径最大，在本研究范围内，总流量分配最均匀的当量直径为0.31 mm,对应的通道高宽为0.33 mm×0.30 mm，即当量直径最大、通道高宽比接近1的换热器流量分配最均匀，换热能力最好。

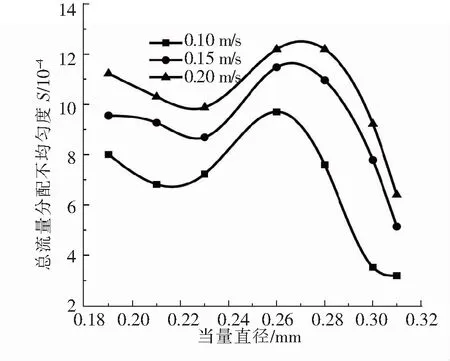
图4 不同当量直径对S的影响

(2)阻力特性。图5为进口速度0.10、0.15、0.20 m/s时不同类型换热器进出口压降。从图5可以看出，随着通道当量直径的增加，换热器进出口压降逐渐减小，当量直径为0.31 mm时换热器进出口压降达到最小值，在实验范围内比压降最大的换热器下降了38.5%。由此可以看出，在当量直径改变但通道面积不变的换热器中，当量直径为0.31 mm,即通道高宽比接近1的换热器,进出口压降最小，换热效果最好。

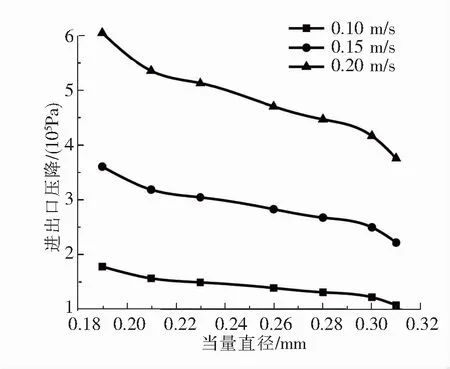
图5 不同当量直径对压降的影响

3.2 不同高宽比对通道流动特性的影响

为了研究不同高宽比对流动特性的影响，设定通道宽度为0.30 mm，高宽比范围0.2～2.4。

(1)流量分配均匀性。图6为液体工质入口速度为0.10、0.15、0.20 m/s，通道宽度为0.30 mm时不同高宽比换热器总流量分配均匀度情况。由图6可以看出，3种进口速度下换热器总的通道流量分布规律相似，均随着高宽比的增加先减小后增大再减小再增大，且随着进口速度的增大，总流量分配峰值出现的时间提前。决定通道内流量大小的主要因素是通道出入口的静压差，随着速度的增大，通道进口处动压增大，静压减小。因此对于同一通道，进口速度增大时，通过该通道的流量明显要比速度较小时通过的流量少，导致总流量分配不均匀度峰值提前。另外从图6可以看出，与前面结论相同通道高宽比在1附近，总流量分配均匀度达到最佳。

图6 不同高宽比对S的影响

(2)阻力特性。图7所示为进口速度0.10、0.15、0.20 m/s时，3种速度下换热器进出口的压降规律相同，都随着高宽比的增大逐渐减小。对比分析可知，水入口速度为0.10 m/s时随通道高宽比增大，压降变化幅度最小，因此从压降的角度考虑，在满足换热要求情况下，选择通道进口速度时要尽量小。

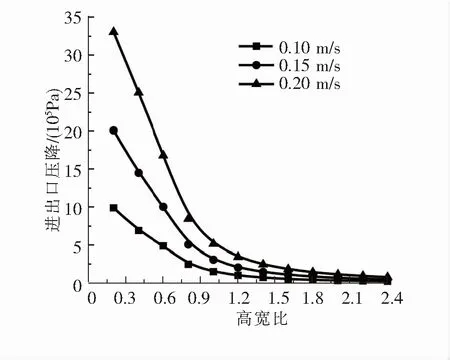
图7 不同高宽比对压降的影响

3.3 不同通道数对通道流动特性的影响

(1)流量分配均匀性。图8为液体工质入口速度为0.10、0.15、0.20 m/s，不同通道数的换热器总流量分配均匀度情况，通道长宽都为0.3 mm，进出口大小为1 mm。由图8可以看出，3种进口速度下换热器总的通道流量分布规律相似，均随着通道数的增加先减小后增大再减小，在本研究范围内，流量分配最均匀的通道数为6通道。这是由于水进入联箱后，在进入通道前正好发展成6通道宽度的流体，能使流量均匀地分配到各个通道中去，通道数太多或太少都不利于换热器整体的流量分配。

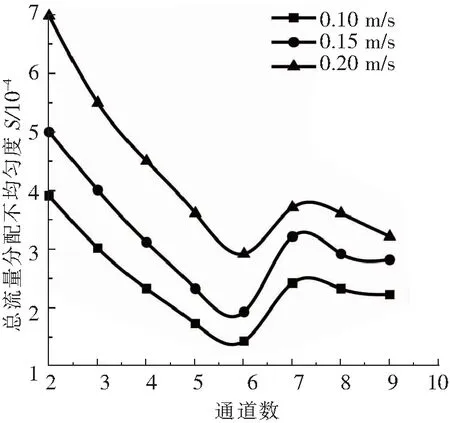
图8 不同通道数对S的影响

(2)阻力特性。图9为进口速度0.10、0.15、0.20 m/s时不同类型换热器进出口压降。从图9可以看出，3种不同通道数的换热器压降都随着进出口的增大逐渐减小再增大，在本研究范围内，通道数为6时进出口压降最小，水入口速度为0.10 m/s时随通道数的增加，压降变化幅度最小。因此从压降的角度考虑，在满足换热要求情况下，选择通道进口速度时要尽量小。

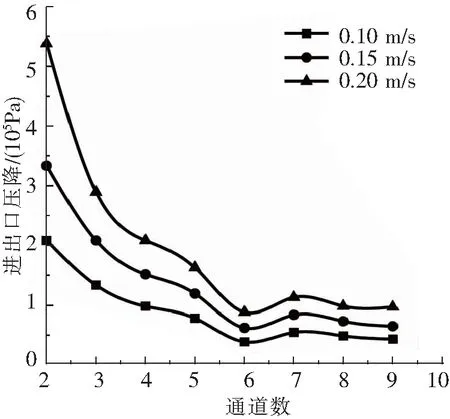
图9 不同通道数对压降的影响

4 结论

对不同通道当量直径、不同高宽比的并联9通道以及不同通道数的换热器在入口速度为0.10、0.15、0.20 m/s 3种情况下流量分配及压降的影响进行了数值模拟，得到以下结论：

(1)换热器通道面积不变，当量直径最大时，流量分配均匀性最好，压降最低。为了达到相对较均衡的流量分配，可将通道做成正方形通道。

(2)为了进一步强化换热，改变换热器通道面积，高宽比接近1时流量分配最均匀，压降较低。为达到相对较均匀的流量分配及压降，在满足加工工艺及结构的基础上，换热器通道形状尽量做成正方形。

(3)通道数对微通道平行流换热器内部流量分配影响较大，在本研究范围内，通道数为6时流量分配最均匀，压降最小。