ω型扣件弹条的非线性力学行为
姜秀杰,刘 艳,2,汤继新,李秋彤,2,赵 威,刘 欢
(1.上海材料研究所,上海 200437;2.上海消能减震工程技术研究中心,上海 200437;3.宁波市轨道交通集团有限公司,宁波 315101;4.上海第二工业大学环境与材料工程学院,上海 201209)
0 引 言
扣件系统是轨道结构的重要组成部分,用于连接钢轨和轨枕并将钢轨扣压在轨枕上,起到保持轨距以及阻止钢轨纵横向移动的作用。扣件系统利用弹条变形弹性储能缓解车辆运行时产生的机械振动以及对轨道的冲击作用。但是,弹条在服役过程中产生的周期性弯曲和扭转组合变形,易导致扣件弹条发生疲劳断裂。
国内外学者对弹条的失效问题进行了大量针对性的研究。齐少轩等[1]研究了Ⅱ型弹条的静态力学行为,指出当弹条的预压缩量和压紧位移超过限值后,弹条后肢弯位置易发生折断。武青海等[2]对比了Ⅲ型扣件中弹条在不同边界处理方法下的力学行为,并应用残余应力的概念分析了弹条预压强化机理。张广朋[3]研究了多节点扣件系统协同作用对扣件系统力学性能的影响,发现较大的横向力和紧固扭矩易使弹条发生破坏。李伟强[4]通过对单趾弹条进行建模仿真,得出弹条的最大应力出现在中肢以及趾端过渡小圆弧处。罗曜波等[5]计算出WJ-7型扣件弹条在冲击力作用下的最大应力出现在与铁垫板的接触部位,在列车载荷的反复作用下,裂纹易在该区域萌生并扩展,直至弹条发生疲劳断裂。刘小军[6]分析了弹条在恒幅载荷和焊缝不平顺激扰下的疲劳寿命。杨志超等[7]通过对W1型弹条在静载荷下的力学性能进行仿真,发现弹条的尾肢中部为裂纹萌生与扩展的敏感部位。XIAO等[8]采用ABAQUS和FE-SAFE联合仿真的方式预测了弹条在循环载荷作用下的疲劳寿命。GAO等[9]研究了高频载荷激励下弹条的响应,并对弹条的结构进行了优化。李中等[10]研究了弹条偏转或扣件松动对弹条扣压力的影响。有学者对比了有无钢轨波磨下弹条的最大等效应力、振动位移以及振动加速度特性,指出钢轨波磨的存在加速了弹条的疲劳损伤[11-12];也有学者研究了高速铁路扣件系统疲劳性能的影响因素和断裂机理[13-17]。
由上述研究可发现,既有研究在计算模拟过程中大多采用线弹性模型定义弹条材料,或采用绑定约束定义弹条与扣件系统中其他零部件之间的接触属性。在静载条件下,弹条局部已发生屈服,而在动载条件下弹条与其他部件之间的接触关系也会随着载荷的变化而发生改变[11,15-16],因此使用线弹性模型定义弹条材料或将弹条与其他零部件之间设置成绑定约束不能模拟弹条的真实受力状态。基于此,作者以我国高铁中普遍采用的Vossloh300-1型扣件系统中的ω型SKL15弹条为研究对象,设置3种材料属性(线弹性模型、双线性模型、拉伸试验获取的弹塑性模型)和2种接触属性(绑定约束、非线性接触),基于有限元软件对弹条的力学行为进行模拟,通过疲劳试验验证仿真结果的有效性,并采用该模拟方法研究了弹条的本构模型以及弹条与嵌入块的接触属性对模拟结果的影响,以期为提高计算精度、模拟弹条在实际运营线路中的力学行为提供更加可靠的指导意见。
1 计算模型
1.1 有限元模型的建立
Vossloh300-1型扣件系统由螺栓、螺栓垫片、绝缘垫片、弹条、轨距挡板、轨下垫板、铁垫板、弹性垫板和绝缘套管等组成。根据弹条元件疲劳试验的组装方式,建立包含弹条、嵌入块和支撑块在内的有限元模型,如图1所示。模型中的弹条采用四面体二次单元(C3D10),共计23 268个节点,14 155个网格;支撑块采用六面体线性非协调模式单元(C3D8I),共计808个节点,543个网格;嵌入块采用四面体二次单元(C3D10),共计15 933个节点,8 883个网格。

图1 ω型弹条扣件系统的有限元模型Fig.1 Finite element model of ω-type spring clip rail fastening system
1.2 材料参数
参考文献[10],扣件系统中各部件的材料参数见表1。

表1 ω型弹条扣件系统各部件的材料参数
为完整定义弹条材料的应力-应变关系,参照GB/T 228.1—2010。在弹条的中肢部分截取拉伸试样,采用SHT4605型万能试验机进行室温拉伸试验,拉伸速度为2 mm·min-1。将试验输出的工程应力-应变曲线转化为真应力-真应变曲线,转换公式为
σt=σn(1+εn)
(1)
εt=ln(1+εn)
(2)
式中:σt为真应力;σn为工程应力;εt为真应变;εn为工程应变。
弹条的真应力-真应变曲线如图2所示,可知弹条的屈服强度σs为1 242 MPa,抗拉强度σb为1 350 MPa。

图2 拉伸试验得到弹条的真应力-真应变曲线Fig.2 True stress-true strain curve of spring clip obtained from tensile test
1.3 边界条件及载荷设置
仿真模型是根据弹条元件的疲劳试验建立的,因此边界条件和载荷输入均与弹条元件的疲劳试验保持一致。约束嵌入块和支撑块3个方向的自由度。弹条各部分的名称如图3所示,为准确分析弹条的受力特点,约束弹条中圈y方向的位移,约束弹条趾端x和y方向的位移[5,7,18-19]。对弹条趾端施加初始静态位移和动态循环位移,其位移幅值分别为9.8,0.7 mm。在受力状态下,弹条与支撑块及嵌入块间均存在接触行为,计算时将弹条与支撑块之间设置为绑定约束,弹条与嵌入块之间设置成摩擦接触。

图3 弹条各部分的名称Fig.3 Names of each part of spring clip
2 疲劳试验及仿真模型验证
2.1 疲劳试验
相关文献[11,19]中的有限元模拟结果显示,弹条在疲劳试验中应变最大的点集中在跟端小圆弧内表面。根据应变集中位置及矢量方向,在进行疲劳试验的弹条元件上相应布置微型应变花,弹条左右两侧跟端小圆弧分别为测点1和测点2,试验装置及测试位置和方向如图4所示。先对弹条趾端施加9.8 mm的垂向静态位移,再施加幅值为0.7 mm、频率为16 Hz的动态位移。试验输出通道1的应变为ε0°,通道2的应变为ε45°,通道3的应变为ε90°,主应变方向和主应变的计算公式为

图4 ω型弹条的疲劳试验装置及测试位置和方向Fig.4 Fatigue test device (a) and test positions and directions (b) of ω-type spring clip

(3)
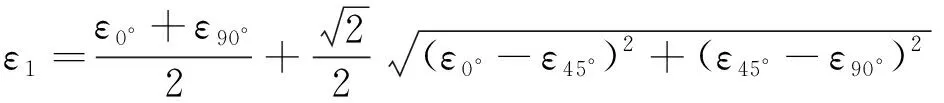
(4)
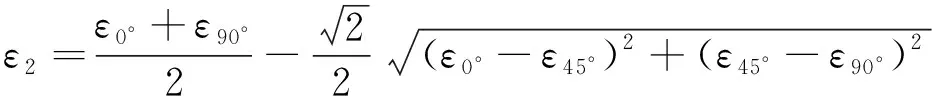
(5)
式中:α0为主应变与水平方向(0°)的夹角;ε1为最大主应变;ε2为最小主应变。
2.2 试验结果及仿真模型的验证
获取弹条各测点在静态位移载荷作用下3个方向的应变,结果如图5(a)所示。对比2个测点的测试结果可知,两者结果基本一致,偏差小于5%。以测点1为例,由式(3)计算得到的最大主应变方向与x轴的夹角约为40°,由式(4)得到的最大主应变为0.008 671。在弹条与嵌入块的接触属性为非线性接触以及弹条本构模型为弹塑性模型的条件下,对弹条的力学行为进行模拟。由图5(b)可以看出,弹条跟端最大主应变方向约为42°,最大主应变为0.008 374,与由图5(a)计算得到的结果具有良好的一致性,相对误差分别为5%,3.4%,验证了该计算模型的有效性。
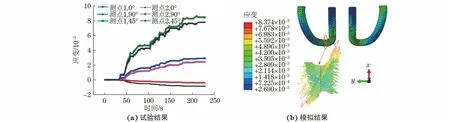
图5 由疲劳试验和有限元模拟得到ω型弹条的最大主应变方向及最大主应变Fig.5 Maximum principal strain and its direction of ω-type spring clip obtained by fatigue test and finite element simulation
3 非线性力学行为的影响因素
采用上述建立的有限元模型研究弹条本构模型和接触属性对弹条非线性力学行为的影响规律,4种不同工况列于表2中。不同本构模型下弹条的真应力-真应变曲线如图6所示,其中:弹塑性本构关系由图2中的完整拉伸试验曲线定义;线弹性本构关系中弹性模量保持不变,可由拉伸试验中应力-应变曲线的直线段延长得到;双线性模型由连接屈服强度和抗拉强度两点确定塑性阶段曲线得到[6,20]。

表2 弹条力学性能的有限元模拟工况
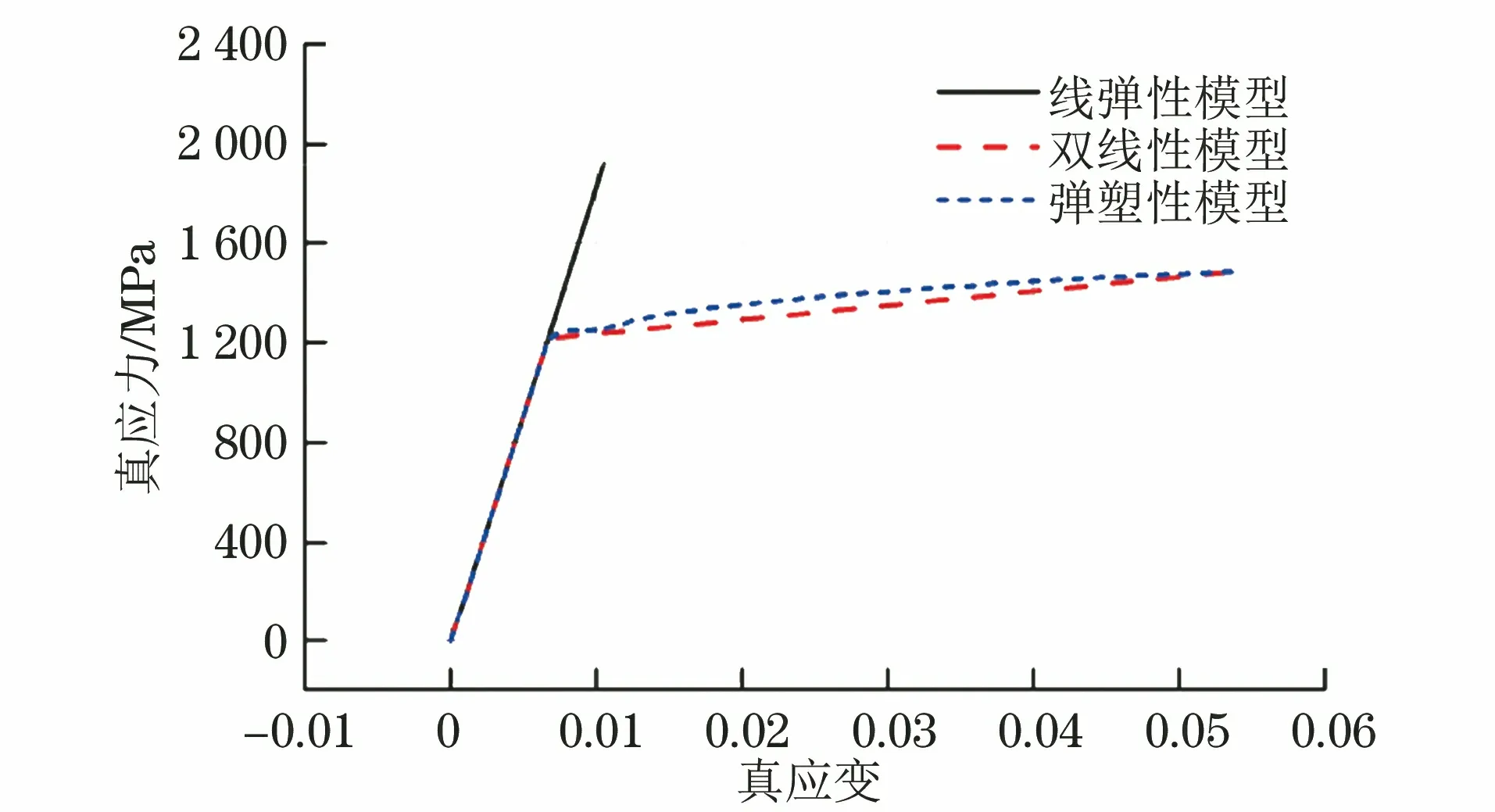
图6 不同本构模型下弹条的真应力-真应变曲线Fig.6 True stress-true strain curves of spring clip with different constitutive models
3.1 本构模型
3.1.1 低频激励条件下
在弹条与嵌入块的接触属性相同的条件下,对线弹性模型、双线性模型和弹塑性模型,即工况1、工况2和工况3下弹条的非线性力学行为进行模拟。先对弹条趾端施加9.8 mm的垂向静态位移模拟疲劳试验中的组装变形,再施加幅值为0.7 mm、频率为16 Hz的动态位移,模拟得到组装状态下弹条的位移和Mises等效应力云图分别见图7和图8。由于低频激励下施加的是位移载荷,所以不同模型下弹条的变形云图是一致的。由图7可知,最大位移出现在弹条趾端,中肢位置基本保持不变。由图8可知:3种本构模型下最大等效应力均出现在弹条跟端小圆弧区域;双线性和弹塑性本构模型下的应力在弹条跟端小圆弧区域变化平缓,而线弹性本构模型下的弹条应力较大值相对集中。

图7 低频激励条件下不同本构模型模拟得到弹条的垂向位移云图Fig.7 Vertical displacement contour of spring clip with different constitutive models under low frequency excitation condition

图8 低频激励下不同本构模型模拟得到弹条的应力云图Fig.8 Stress contour of spring clip with different constitutive models under low frequency excitation: (a) linear elastic model; (b) bilinear model and (c) elastic-plastic model
图9中0~1 s内施加的是静态位移载荷,1 s后施加的是动态位移载荷。由图9可以看出,尽管双线性模型下弹条的弹性应变略小于弹塑性模型下的,但其屈服后塑性应变大于弹塑性模型下的,导致真应变略大于弹塑性模型下的,但整体看双线性模型和弹塑性模型计算得到的弹条力学特性基本一致。采用双线性和弹塑性本构模型可准确获得弹条跟端在静态安装状态下的塑性变形。由于弹条跟端局部区域进入屈服阶段(时间大于0.6 s)后开始产生显著的塑性变形,其塑性应变大于弹性应变;而线弹性本构模型高估了弹性应变,其计算得到的真应力远大于采用双线性和弹塑性本构模型得到的真应力。时间超过1 s后在动态位移载荷下,双线性和弹塑性本构模型模拟发现弹条跟端的塑性应变先出现瞬时增大的现象,而后趋于平稳,这是由于动态位移载荷在初始的1/4个周期内的方向与静态位移载荷一致,使塑性变形程度增大,而后在循环卸载-加载过程中塑性形变程度不再增加。通过平移动态位移载荷作用下弹条跟端的应力、应变与时间的关系曲线,可知3种本构模型下的弹性应变、真应变和主应力基本一致。

图9 低频激励下不同本构模型模拟得到弹条跟端的时程响应曲线Fig.9 Time history response curves of spring clip with different constitutive models under low frequency excitation: (a) maximum plastic strain; (b) maximum elastic strain; (c) maximum true strain and (d) maximum principle stress
3.1.2 高频激励条件下
为研究弹条在接近共振状态下的位移、应变等响应特征,将加载方式改为力加载。为保证除频率以外的其他加载条件与低频激励工况的一致,先在第一个载荷步中对弹条趾端施加8.1 kN的静态载荷,模拟弹条疲劳试验中的组装变形(静态初始位移约9.8 mm),然后将第二个载荷步中所施加的动态载荷频率设为一阶固有频率343 Hz,该频率由图1的仿真模型计算得到,载荷幅值为0.6 kN,动态位移幅值约为0.7 mm。由于弹条趾端、跟端和中肢的边界条件、安装方式、加载方式等均与组装扣件系统中的弹条元件存在差异,因此该模态频率小于同类扣件系统一阶组装模态频率(480~570 Hz)[21]。
由于静态加载(0~1 s)的响应特征与低频激励工况下的基本一致,此处不再赘述。在共振频率(343 Hz)动态加载的激励下,弹条趾端位移和跟端应变、应力时程响应曲线分别见图10和图11。由图10可知,在共振频率动态加载激励下,3种本构模型弹条趾端的动态位移均出现共振放大现象,线弹性模型下的动态位移幅远大于双线性模型和弹塑性模型下的。由图11可以看出:双线性模型和弹塑性模型下因共振导致的位移响应放大,弹条跟端局部区域出现塑性应变累积现象,其最大塑性应变、真应变、主应力的均值逐渐增加;线弹性模型下最大真应变幅和主应力幅增大,但均值保持不变。

图10 共振状态下不同本构模型模拟得到弹条趾端的垂向位移Fig.10 Vertical displacement of spring clip toe with different constitutive models in resonance state
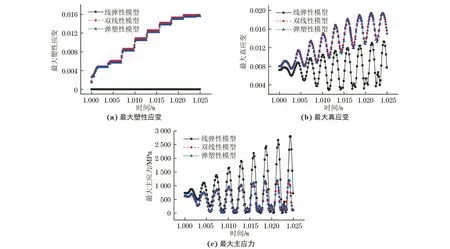
图11 共振状态下不同本构模型模拟得到弹条跟端的时程响应曲线Fig.11 Time history response curves of spring clip heel with different constitutive models in resonance state: (a) maximum plastic strain; (b) maximum true strain and (c) maximum principle stress
3.2 接触属性
在弹性本构模型均为弹塑性模型的条件下,对弹条和嵌入块的接触属性分别为绑定约束和非线性接触,即工况3和工况4下弹条的非线性力学行为进行模拟。使用主从公式定义表面的绑定约束,该约束可防止从属表面和主控表面分离或产生相对滑动,且从属表面不穿透主控表面[8]。非线性接触中的法向接触采用有限元软件中的硬接触,即两物体间不允许相互贯穿或侵入,且力只能是压力;切向接触采用库伦摩擦模型,并且引入一个允许弹性滑动的罚摩擦公式。弹性滑动是在黏结的接触面之间发生的小量相对运动,有限元软件可自动地选择罚刚度[8]。
3.2.1 低频激励条件下
在低频激励条件下,先对弹条趾端施加9.8 mm的垂向静态位移模拟疲劳试验中的组装变形,再施加幅值为0.7 mm、频率为16 Hz的动态位移。由图12可知,在静态和动态位移载荷作用下,当弹条跟端与嵌入块间为绑定约束时,弹条跟端塑性应变、弹性应变、真应变以及主应力均大于非线性接触时的结果。主要原因是,在静态及动态位移载荷作用下,为达到相同的趾端位移,绑定约束条件下需要提供更大的力,且与非线性接触相比对弹条跟端的约束更为严格,这就导致应变、应力响应均大于非线性接触。

图12 不同接触属性下弹塑性模型弹条跟端的时程响应曲线Fig.12 Time history response curves of spring clip heel with elastic-plastic model under different contact properties:(a) maximum plastic strain; (b) maximum elastic strain; (c) maximum true strain and (d) maximum principle stress
3.2.2 高频激励条件下
为研究弹条在接近共振条件下的响应特性,先对2种接触属性的模型进行模态分析,进而采用载荷控制方式进行加载。由于边界条件对弹条固有频率具有较大影响[8],因此表3仅列出前2阶模态频率,可知非线性接触模型的模态频率小于绑定约束模型的。在静态和动态载荷幅值分别为8.1 kN和0.6 kN条件下对模型进行强迫共振激励。

表3 不同接触属性下弹条的模态频率
由图13可以看出:非线性接触条件下弹条趾端的静态位移响应大于绑定约束条件下的,这是由于绑定约束限制了弹条跟端的全部自由度,弹条不易变形所致;在动态载荷作用下,2种接触属性下弹条趾端的动态位移都出现了振动放大现象,非线性接触下的动态位移幅略大于绑定约束下的。由图14可知:非线性接触条件下弹条在静态载荷下的塑性应变、真应变以及主应力响应大于绑定约束条件下的;在动态载荷作用下,由于塑性应变累积,2种接触属性下的塑性应变都逐渐增大,且非线性接触条件下的增长速率明显较大;非线性接触下的最大主应变幅和主应力幅也略大于绑定约束下的,这是由于绑定约束条件限制了弹条跟端的全部自由度,弹条不易变形。
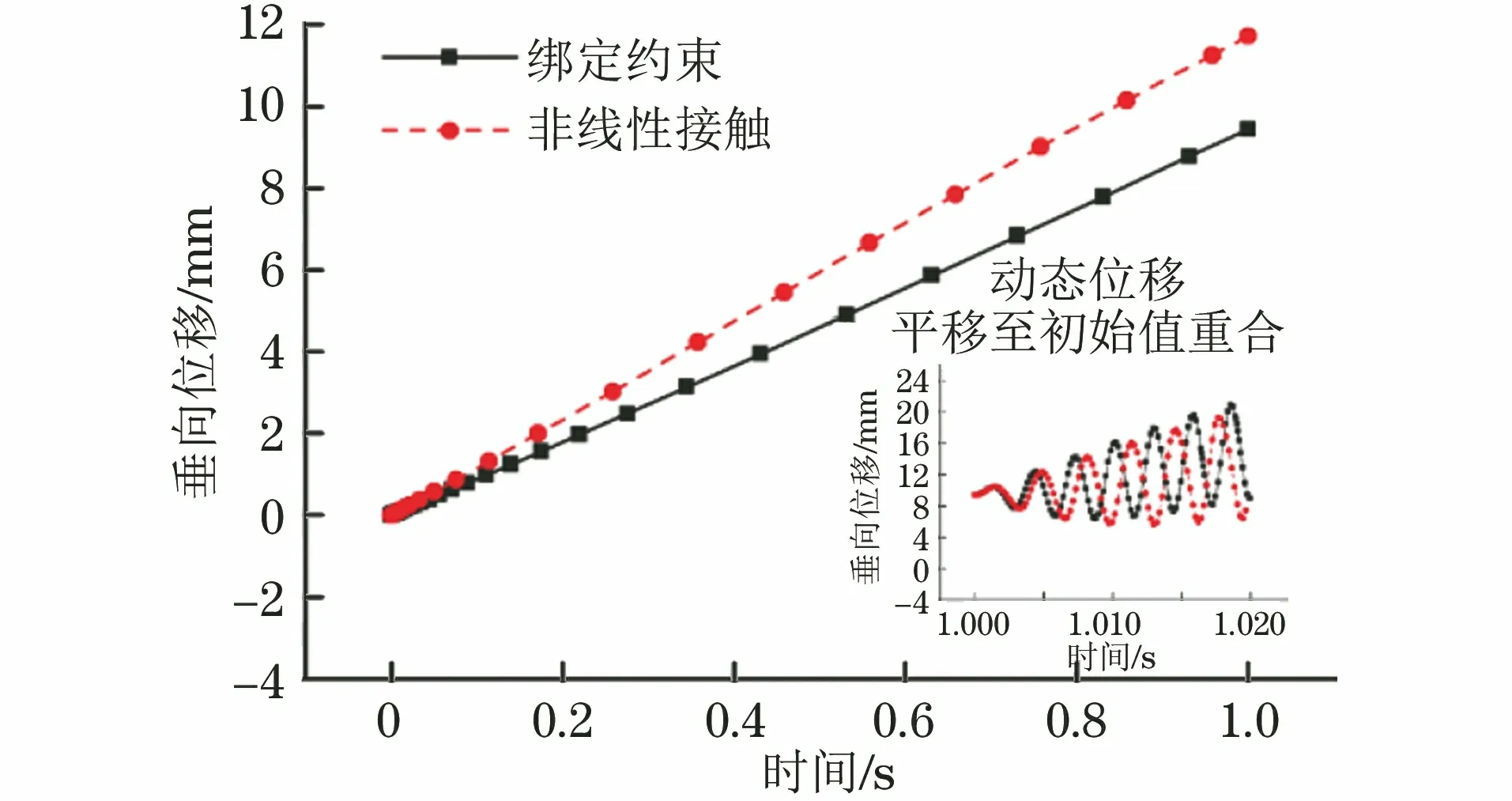
图13 不同接触属性下弹塑性模型模拟得到弹条趾端的垂向位移Fig.13 Vertical displacement of spring clip toe with elastic-plastic model under different contact properties
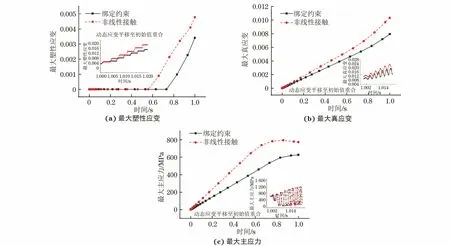
图14 不同接触属性下弹塑性模型模拟得到弹条跟端的时程响应曲线Fig.14 Time history response curves of spring clip heel with elastic-plastic model under different contact properties: (a) maximum plastic strain; (b) maximum true strain and (c) maximum principal stress
4 结 论
(1) 在弹条与嵌入块的接触属性为非线性接触以及弹条本构模型为弹塑性模型的条件下,采用有限元模拟得到的弹条跟端最大主应变方向及最大主应变与试验结果相吻合,二者的相对误差分别为5%和3.4%,验证了计算模型的有效性。
(2) 弹条材料的本构模型对弹条力学行为具有较大的影响。线弹性模型高估了弹性应变,与弹条元件的实际服役条件不符;接近共振频率激励下,双线性模型和弹塑性模型模拟发现弹条跟端出现塑性应变累积现象,和实际情况吻合,而线弹性模型模拟结果显示弹条中未出现该现象,与实际情况不符;双线性模型是在弹塑性模型基础上进行一定简化得到的。因此在有限元模拟中,推荐采用弹塑性模型进行分析。
(3) 非线性接触属性对弹条力学行为影响显著。在低频动态位移载荷下,非线性接触条件下弹塑性模型模拟得到弹条的位移、应力和应变均小于绑定约束条件下的;静态载荷和共振频率动态载荷激励下,非线性接触条件下弹条位移、应力和应变均大于绑定约束条件下的。在实际应用中,弹条与嵌入块及轨距挡板之间存在相对位移,为提高仿真精度,建议弹条与嵌入块间设置非线性接触。

