圆孔衍射中心显现亮暗斑的实验设计与实施

王 雁,邴 辉

(1.沈阳市第二中学，辽宁 沈阳 110016;2.抚松县第一中学，吉林 白山 134500)

《高中物理课程标准》对光的波动性要求是：观察光的干涉、衍射和偏振现象，掌握这些现象产生的条件，了解其在生产生活中的应用[1].学生在生活中对光的直线传播、反射、折射的现象已深有体会，但是对光的波动性引起的干涉、衍射等现象非常陌生.泊松亮斑是较为典型的由光的波动性引起的衍射现象[2]，高中物理教材对此也有一定的介绍.其中《普通高中教科书·物理》(选择性必修第一册)[3]中“黑暗中心的光明”现象引起了师生的极大兴趣，然而“光明中心的黑暗”现象却往往被忽视，这导致很多师生没有见过圆孔衍射图样中心斑点为暗斑的现象.在衍射实验教学过程中，教师通过移动光屏能够让学生观察到衍射图样中心出现忽亮忽暗的现象，该现象对于学生认识光的波动性具有重要意义.基于以上情况，本文对圆孔衍射进行理论分析和参量对比，采用简单的实验器材在课堂上为学生演示出了丰富的衍射现象.

1 实验原理

圆孔衍射现象是在点光源(或激光束)的照明空间中插入带圆孔的衍射屏,接收屏幕上出现亮暗相间的互为同心圆的衍射条纹图样,中心斑点可能是亮的(亮斑),也可能是暗的(暗斑)，该现象可利用半波带法来解释.

取波前Σ作为以点光源S为球心的球面(等相面),设其半径为R,其顶点O与场点P0的距离为b,以P0为中心,分别以b+λ/2,b+λ，b+3λ/2,b+2λ，…为半径做球面，其中λ为光的波长.将波前Σ分割为一系列环形带，分隔点为M1,M2,M3，…，其中M1,M2,M3，…到P0的光程逐次相差半个波长,故将此环形带称作半波带，如图1所示[4].根据计算，可得到第1个半波带的半径为

图1 半波带法的光线示意图

(1)

第k个半波带的半径为[4]

(2)

在波前Σ处放置带圆孔的衍射屏.一般来说,当该圆孔包含奇数个半波带时,衍射图样中心为亮斑；包含偶数个半波带时,衍射图样中心为暗斑.

根据式(2)可得出

(3)

令圆孔半径Rd=ρk，则ρk可通过测量孔径得到，再代入式(3)即可求出衍射图样中心出现暗斑与亮斑时对应的接收屏位置b.k取偶数时,求得的b值对应的是衍射图样中心为暗斑时接收屏的位置；k取奇数时，求得的b值对应的是衍射图样中心为亮斑时接收屏的位置.

根据式(3)可知，k越小，b越大，由于b为正数，因此k有最小值.当k取最小正整数时，可得到b的最大值.该最大值的意义是：在控制λ和Rd不变时，bmax以外位置的衍射图样中心不会有亮暗变化，即观察衍射图样中心有亮暗变化的范围需小于bmax.另外，若接收屏距离圆孔太近，即小于1 m时，接收屏上的衍射图样直径小、亮度高，导致人眼很难分辨图样中心的亮暗.因此，人眼能够清晰观察到衍射图样中心亮暗变化的孔屏距离范围是1～bmax.通常，人们习惯选择Rd<1 mm的圆孔，此时，计算出的bmax<1 m,根据上述分析可知该范围难以观察到衍射图样中心的亮暗变化.因此，在课堂上的演示实验过程中，若想让学生能够较明显地观察到衍射图样中心亮暗变化的现象，须合理选择参量的大小.

2 实验参量探究

对圆孔半径Rd、光源到圆孔的距离R与接收屏位置b的关系进行探究.

2.1 圆孔半径Rd与接收屏位置b的关系

根据理论分析结果，利用几何画板软件，通过改变Rd的大小对圆孔衍射现象进行模拟实验.设光源S到圆孔的距离R=0.38 m,激光波长λ=623.8 nm,亮(暗)斑位置可通过Rd和k来确定，实验数据如表1所示.考虑衍射图样不能太小，且亮度不能过高，因此须满足bmax>1 m.结合表1中数据，若想要较明显地观察到衍射图样中心亮暗变化的现象，则当Rd=1.17 mm时，须在距离圆孔0.99～9.75 m范围内移动接收屏；当Rd=1.50 mm时，须在距离圆孔1.44～7.10 m范围内移动接收屏；当Rd=2.50 mm时，须在距离圆孔3.80～15.80 m范围内移动接收屏.

表1 不同Rd时，几何画板模拟出的亮(暗)斑位置

2.2 光源到圆孔距离R与接收屏位置b的关系

当圆孔半径Rd=2.50 mm,λ=623.8 nm,改变R的大小，利用几何画板软件对圆孔衍射现象进行模拟实验，模拟数据如表2所示，可以看出R变化1 cm，衍射图样中心的亮(暗)斑位置则有较大变化，并且光源到孔距离越近(即R越小)，同一k值对应的接收屏位置就越远(b越大).因此教师在课堂上进行演示实验时，一般选择R=0.38～0.39 m，对应接收屏的位置在4 m左右，此时学生能够较明显地观察到衍射图样中心亮暗交替的有趣现象.

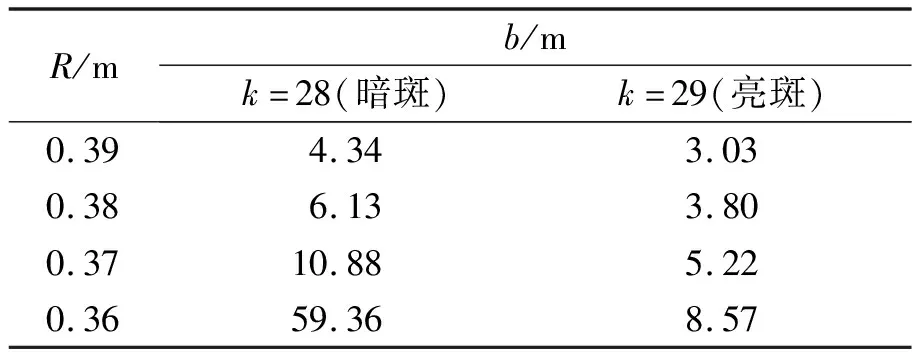
表2 不同R时，几何画板模拟出的亮(暗)斑位置

3 实验方法

实验器材：氦氖激光演示仪(λ=623.8 nm)、铁架台(2个)、带圆孔的钢板尺、凸透镜、双面胶带、卷尺、接收屏(贴有白纸的木板).

实验步骤为：

1)按图2放置实验仪器(接收屏除外).

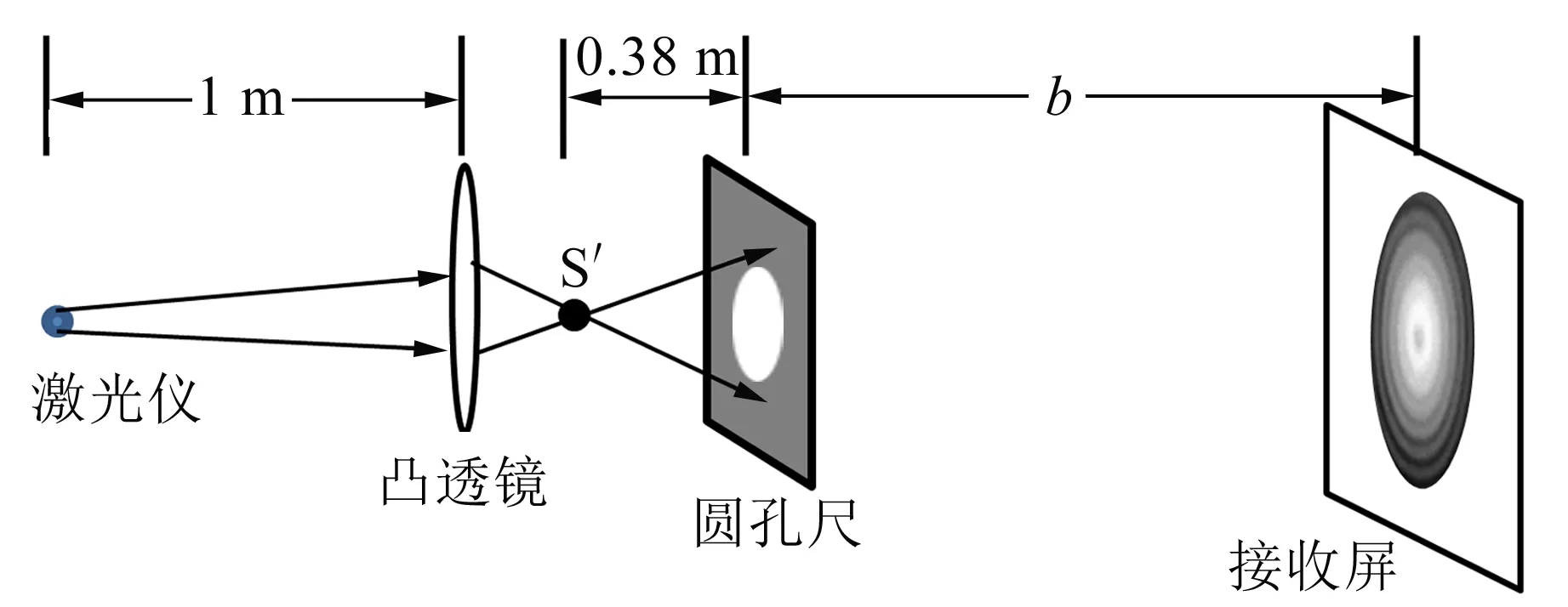
图2 实验装置示意图

2)调整激光演示仪和凸透镜，使二者之间的水平距离约为1 m，且光束能够垂直穿过凸透镜的中心.

3)将接收屏放置在凸透镜与圆孔尺之间，移动接收屏，观察接收屏上光斑的变化，当光斑会聚成最小最亮的点时，标记此时位置作为等效点光源S′的位置.

4)将接收屏放置在图2所示位置，在圆孔尺上选择一孔，用双面胶封上其他孔.调整圆孔尺，使尺孔与等效点光源S′之间的水平距离为0.38 m，且光束垂直于尺面，保证光束中心与尺孔中心重合,并满足光束的半径大于圆孔半径.

5)参考表1中的位置，移动接收屏，观察衍射图样中心亮暗交替的现象.

6)改变不同孔径，重复实验步骤1)～5)，观察衍射图样中心亮暗交替的现象.

衍射图样如图3所示.

(a)Rd=1.17 mm

4 孔形状对衍射图样的影响

上文分析都是在圆形孔的条件下进行的探究，当孔的形状不是圆形，而是三角形、矩形或六边形时，衍射图样是否依然会出现圆形光斑呢？本文根据该问题进行了拓展探究，即将圆形孔分别换成边长为2 mm的三角形、矩形和六边形的孔，得到如图4所示的衍射图样.从图4中可以看出三角形、矩形和六边形的孔分别呈现出与它们形状相同的衍射图样，这说明孔的形状决定了衍射图样的边界形状.

(a)三角形 (b)矩形 (c)六边形

有师生猜想上述现象可能与孔径较大有关，为探究该问题，本文选取不同边长的三角形孔进行了拓展实验，得到如图5所示的衍射图样.从图5可以看出，当边长a=2 mm时，衍射图样的边界亮而清晰，衍射条纹与边界平行，宽度较窄，边界形状与孔的形状一致；当边长a=0.5 mm时，衍射图样的边界变得模糊，中心处更亮，衍射条纹变宽，边界形状与孔的形状相近.因此，衍射图样与孔的形状及大小都有关系.

图5 边长逐渐减小的三角形孔的衍射图样

5 结束语

本文通过实验原理分析和理论公式推导深化了物理学科素质教育，培养了学生科学推理、科学论证、质疑创新等物理学科核心素养.在课堂上的演示实验过程中，学生参与了实验的全过程，在不同孔径和不同孔形条件下，观察到了丰富多样的衍射图样，直观地体验了由光的波动性引起的衍射现象.该演示实验激发了学生对探究科学知识的兴趣和热情，培养了学生的创造力，并全面提升了学生的科学探究素养.