基于奇异谱分析的γ能谱降噪算法
赵思文,吴 怡,王崇杰
(辽宁师范大学 物理与电子技术学院,辽宁 大连 116029)
γ能谱分析是放射性核素分析及核材料类型识别的重要技术手段,广泛应用于环境监测、核武器核查、宇宙探测以及核安全保障等领域[1-6].然而,γ能谱中存在的噪声给γ能谱分析与识别带来较大困难,甚至导致错误结果(特别是对于低水平放射性分析和差异甚微的核材料识别[2-4]).因此,降噪处理是γ能谱分析与识别过程中重要的技术环节.
传统的γ能谱降噪方法主要有道址域的曲线拟合移动平滑法和频域的滤波法[7-8].移动平滑法容易引起谱线变形、失真,甚至畸变[8].频域滤波法是目前较常用的γ能谱降噪方法,其中主要有基于快速傅里叶变换(Fast Fourier transform,FFT)和小波变换(Wavelet transform,WT)的线性滤波法[8-9].γ能谱噪声的频谱通常是全域的,与γ能谱成分的频谱严重重叠,传统的频域滤波法难以对噪声和谱成分进行有效分离.因此,常常存在降噪不充分或降噪过度的现象.另外,除加性噪声外,γ能谱还含有乘性噪声,而传统的降噪方法往往忽视γ能谱的乘性噪声[9],导致降噪效果不理想.
奇异谱分析(Singular spectrum analysis,SSA)是在奇异值分解理论基础上兴起的独立于信号模型的无参量频谱估计技术[10],已成功应用于信号的降噪处理[11-12].该技术具有不受噪声频谱分布影响和自适应降噪的特点[12].本文首先提出了基于SSA的γ能谱降噪方法,并介绍了降噪的基本原理与具体算法.其次,通过分析γ能谱的奇异谱特征,对轨迹矩阵嵌入维数和重构奇异值阶数的最优取值方法进行了研究和讨论.最后,对实测60CoHPGe γ能谱进行了降噪处理,并与传统的FFT和WT滤波法进行比较,验证了降噪算法及其参量选取方法的有效性.
1 基于SSA的γ能谱降噪原理
基于奇异谱分析的γ能谱降噪算法的基本思想是:首先通过构建轨迹矩阵将一维γ能谱数据映射到高维相空间;然后对轨迹矩阵进行奇异值分解,并根据奇异谱的特征对γ能谱成分和噪声成分进行分离,较大的奇异值对应γ能谱成分,较小的奇异值则对应噪声成分;最后利用较大奇异值成分对γ能谱进行重构,从而达到降噪的目的.降噪算法包括4个步骤:轨迹矩阵嵌入、奇异值分解、奇异值分组和对角平均化[10-12].
1)轨迹矩阵嵌入.设x1,x2,…,xN′为一维γ能谱数据,则相应γ能谱的L×K轨迹矩阵为
(1)
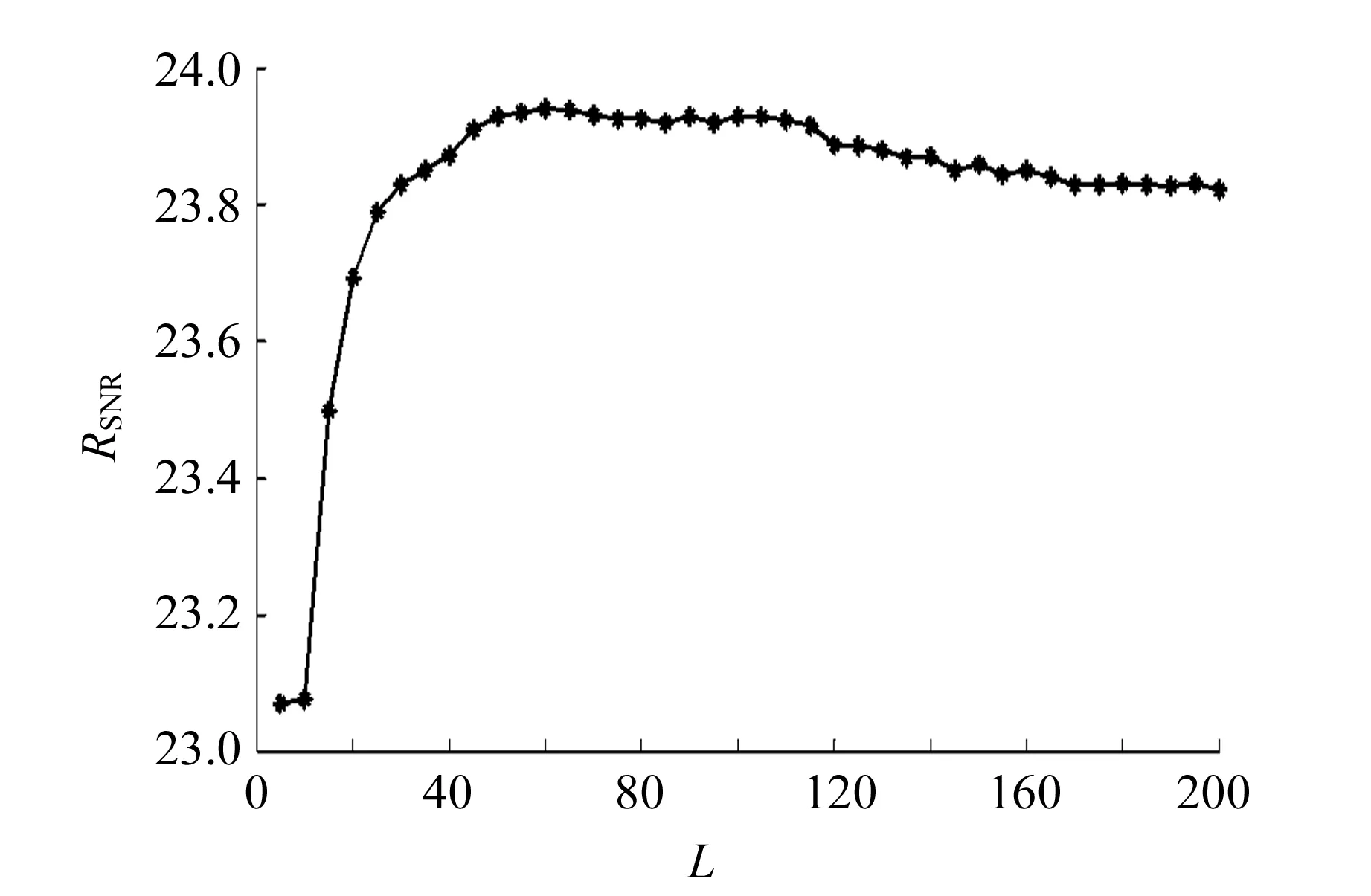
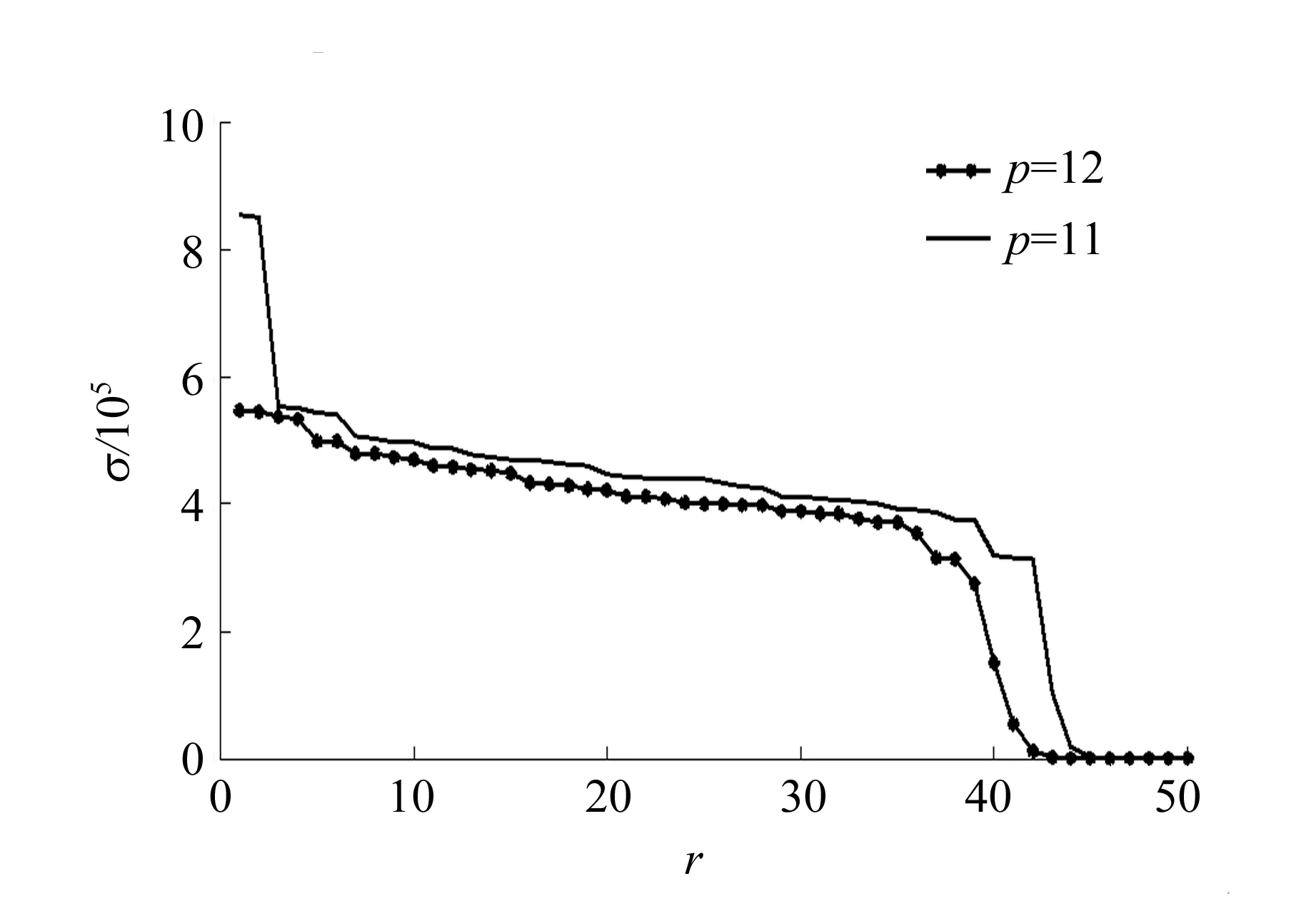
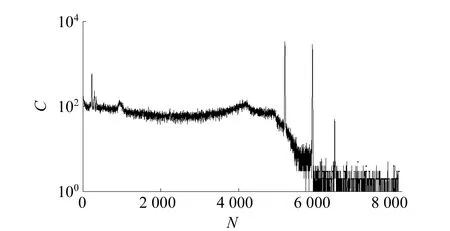
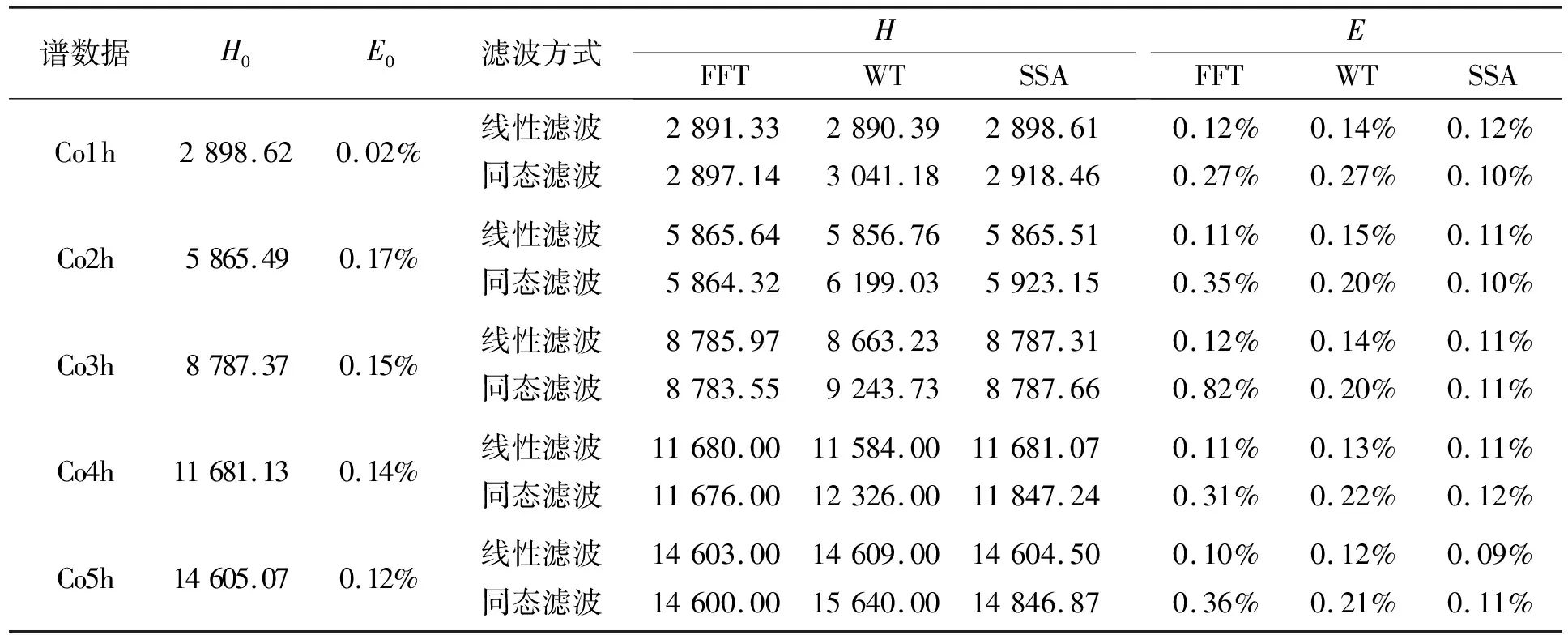
式中,N′为γ能谱的最大道址数,L为嵌入维数,1 2)轨迹矩阵奇异值分解.对轨迹矩阵X进行奇异值分解 (2) 式中,d=rank(X)是轨迹矩阵的秩,即X的非零奇异值个数,且d≤min(L,K).σ1,σ2,…,σd为降序排列的非零奇异值,向量ui∈RL×1和向量vi∈RK×1(i=1,2,…,d)分别为轨迹矩阵X的左奇异向量和右奇异向量. 3)奇异值分组.按轨迹矩阵X奇异值的大小,将奇异值分成2组,前r(r (3) 4)对角平均化.对角平均化实质上是将降噪后的轨迹矩阵Y∈RL×K转换成降噪后的γ能谱.设yij为轨迹矩阵Y的元素,则降噪后γ能谱为 (4) 选择恰当的嵌入维数L和重构阶数p,即能达到降低γ能谱噪声的目的. 选用EG&G ORTEC 918A-HPGe γ能谱仪,多道分析器最大道址为8 192,谱仪系统在60Co 1 332.50 keV处的能量分辨率为2.0 keV.放射源为60Co标准点源,活度为2.75 kBq.测量活时间设置为1,2,3,4,5 h,相应谱数据分别记为Co1h~Co5h. 为了达到最佳的降噪效果,需选择最优的轨迹矩阵嵌入维数L和重构阶数p.关于轨迹矩阵嵌入维数和重构阶数的取值问题,目前还没有通用的准则和方法,相关文献针对不同信号推荐的方法,都具有一定的主观性[12-15].鉴于此,本文对γ能谱的奇异谱特征进行了分析,并研究了γ能谱降噪信噪比随嵌入维数的变化规律.根据γ能谱降噪剩余噪声奇异谱的特征,给出了最优重构阶数的选取方法. 图1是不同嵌入维数情况下Co1h γ能谱的奇异谱.由图1可知,对于不同的嵌入维数L,奇异谱均存在1个拐点,拐点左侧的奇异值较大,而且随着阶数的增加奇异值快速衰减,对应γ能谱成分;而拐点右侧的奇异值较小,且随阶数的变化相对平缓,对应噪声成分.因此,利用奇异谱中的拐点可对谱成分和噪声进行分离,进而通过重构得到降噪γ能谱. (a)不同嵌入维数下的奇异谱 图2是Co1h γ能谱降噪后信噪比随轨迹矩阵嵌入维数L的变化规律,其中信噪比为 (5) 式中,xi是第i个道址上的谱计数,NCH1和NCH2分别是60Co 1 332.50 keV γ射线康普顿平台左右边界能量1 040 keV和1 090 keV所对应的多道分析器道址[16-17]. 由图2可知,当嵌入维数较小时,信噪比相对较低;当L>50时,信噪比变化相对平稳;当L>110时,信噪比则开始缓慢下降.研究表明:当L在50~110区间内取值时,均可获得较大的信噪比和较好的降噪效果,该区间是嵌入维数的最佳取值区间,且与谱数据长度基本无关. 图2 信噪比随嵌入维数L的变化规律 由SSA降噪原理可知,剩余噪声中不含谱成分时所对应的最小重构阶数就是最优重构阶数.上述研究表明,噪声奇异谱与谱成分奇异谱之间的差异十分明显.因此,为确定最优重构阶数,首先在γ能谱奇异谱中分别取拐点r和r-1右侧奇异谱重构剩余噪声谱;然后按下式计算2个剩余噪声谱奇异谱之间的相关系数R[18-19]: (6) 式中,np和np-1分别表示重构阶数为p和p-1时剩余噪声的奇异谱,D为剩余噪声轨迹矩阵的秩;最后,逐步减小p值,当相关系数R明显减小,且小于一定阈值时,相应的p值就是最优重构阶数.由式(6)计算可得,当p<11时,p和p-1所对应剩余噪声奇异谱之间的相关系数R减小,而当p≥11时,R显著增大,且均大于0.92.图3是嵌入维数L=50,重构阶数分别为p=11和p=12时Co1h的剩余噪声奇异谱,二者相关系数R=0.59.因此,p=11即是最优重构阶数. 图3 剩余噪声奇异谱 分别采用线性滤波和同态滤波方式[9],对实测60Co γ能谱进行了降噪处理,并与传统的FFT和WT降噪方法进行比较. 线性滤波是直接对谱数据进行变换或分解,然后通过选取适当的滤波参量消除噪声分量,最后通过逆变换或重构得到降噪γ能谱.同态滤波则用于消除乘性噪声,首先对谱数据进行对数运算,将谱成分与噪声之间的非线性关系转换成线性关系,然后通过线性滤波消除噪声分量,最后通过指数运算得到降噪谱. 在SSA方法中,取轨迹矩阵嵌入维数L=50,利用上述剩余噪声奇异谱相关系数法确定重构阶数.在FFT滤波中,根据γ能谱幅频特性,将幅值小于一定阈值的傅里叶变换系数置为0,再进行逆变换得到降噪谱[16].在WT滤波中,选择对称性和紧支性较好的光滑小波“sym8”为小波基函数,采用小波分解和低频系数进行重构,实现降噪[7-9].在确保谱线不变形的情况下,尽量提高降噪幅值阈值和小波分解层数.在线性滤波和同态滤波中,小波分解层数分别为2和3. 降噪前后的Co1h谱图如图4所示.由图4可看出,SSA法的降噪效果显著,且采用同态滤波降噪效果明显优于线性滤波. (a)原始谱 Co1h~Co5h谱降噪前后信噪比见表1.除Co1h谱的线性降噪结果外,SSA法降噪后信噪比均大于传统降噪方法.采用线性滤波,SSA法降噪后的信噪比提高了20.64%~25.58%,整体高于传统的FFT法(17.89%~26.50%)和WT法(17.83%~26.49%).采用同态滤波,SSA法降噪后的信噪比提高了31.57%~39.16%,高于FFT法(21.08%~25.96%)和WT法(28.23%~35.50%),获得最佳降噪效果.而采用同态滤波降噪信噪比均大于相应的线性滤波降噪信噪比.研究结果表明,SSA法能够降低加性噪声,通过同态滤波方式也降低了乘性噪声,使γ能谱信噪比得到较大幅度提高,较传统频域滤波法具有更强的降噪能力. 表1 降噪前后谱信噪比及其误差 为了进一步探究SSA降噪法对γ能谱的影响,计算了降噪前后60Co谱中1 332.50 keV γ射线特征峰(全能峰)参量.所用峰形函数为[17] (7) 式中,N为道址,H为峰高,Np为峰位,a和b分别为峰本底系数.半高全宽、净峰面积及峰康比分别为 (8) (9) (10) 式中,NCH1和NCH2分别是1 040~1 090 keV能量区间的左右边界道址. 降噪前后谱峰高及其误差如表2所示.由表2可知,在线性滤波方式下,2种传统频域滤波法对峰高无明显影响,而SSA降噪法对峰高几乎无影响.在同态滤波方式下,FFT法降噪后峰高亦无明显变化,而SSA法降噪后峰高略有增加,WT法降噪后的峰高明显提高.研究表明:FFT属于时-频全局变换,而γ能谱中噪声频谱与谱成分频谱存在交叠,频域滤波过程中容易造成谱成分损失,从而使峰高降低.WT属于时-频局域变换,在同态滤波方式下能更有效地降低乘性噪声而使峰高得到较大幅度提高[9],但降噪效果与小波函数的对称性、连续性等密切相关,如果小波函数选择不当,容易引起谱线局部畸变.SSA降噪法则是在相空间通过对谱数据的奇异值分解和重构实现降噪,而且噪声奇异谱与谱成分奇异谱之间的差异明显,最优重构阶数的确定不受噪声频谱的影响.因此,不会造成过度降噪而使峰高降低和谱线变形等现象,并且在同态滤波方式下,也可以更有效地分离和降低乘性噪声,从而使峰高有所增加. 降噪前后谱半高全宽及其误差如表3所示.由表3可知,采用线性滤波,SSA,FFT和WT 3种降噪法对全能峰半高全宽的影响均很小,尤其是SSA降噪法对半高全宽几乎没有影响.采用同态滤波,FFT法对半高全宽的影响亦很小,而SSA法降噪后半高全宽略有减小,WT法降噪后半高全宽则显著减小.结合表2可知,在同态滤波方式下,SSA法与WT法在使峰高增大的同时使半高全宽减小,而且峰高与半高全宽的相对变化幅度基本相同. 表2 降噪前后谱峰高及其误差 表3 降噪前后谱半高全宽及其误差 降噪前后谱峰康比及其误差如表4所示.由表4可知,在线性滤波方式下,与传统频域滤波降噪方法相同,SSA法降噪后峰康比基本保持不变.在同态滤波方式下,FFT法降噪后的峰康比亦保持不变,而SSA法降噪后的峰康比有小幅提高,WT法降噪后的峰康比提高幅度相对较大.结合表2可知,如果考虑峰本底,峰康比的变化反映了峰高的变化,而康普顿平台没有变化.结果表明:与传统频域滤波方法相同,SSA法降噪不影响谱线整体分布. 表4 降噪前后谱峰康比及其误差 降噪前后峰净面积及其误差如表5所示.由表5可知,与传统频域滤波法相同,无论是线性滤波方式还是同态滤波方式,SSA法降噪后的净峰面积保持不变.说明SSA降噪法能够适用于后续的γ能谱定量分析,进一步表明SSA降噪法是有效的. 表5 降噪前后峰净面积及其误差 SSA降噪法可通过轨迹矩阵将γ能谱映射到相空间,进而在相空间通过奇异值分解和重构实现信噪分离,克服了传统频域滤波方法无法解决的噪声频谱与谱成分频谱的重叠问题.同时,由于轨迹矩阵只与待降噪γ能谱有关,因此,SSA降噪法不易引起谱线变形或畸变.剩余噪声奇异谱相关系数法可确定降噪谱的最优重构阶数,有效避免了传统方法降噪过程中存在的降噪不充分或降噪过度现象.由于受统计涨落的影响,原始谱的信噪比、半高全宽及峰康比等指标的误差相对较大,而降噪后误差明显减小,反映了不同降噪方法的降噪效果.SSA降噪法对全能峰峰高几乎没有影响,因此,降噪不会影响γ能谱的能量线性.综上,SSA降噪法算法简单,具有较好的降噪性能,在采用线性滤波和同态滤波2种滤波方式下均可获得令人满意的降噪效果,是有效的γ能谱降噪方法.2 实测γ能谱降噪处理与结果
2.1 仪器设备与测量
2.2 γ能谱的奇异谱特征及其降噪算法参量的选取

2.3 γ能谱降噪与结果


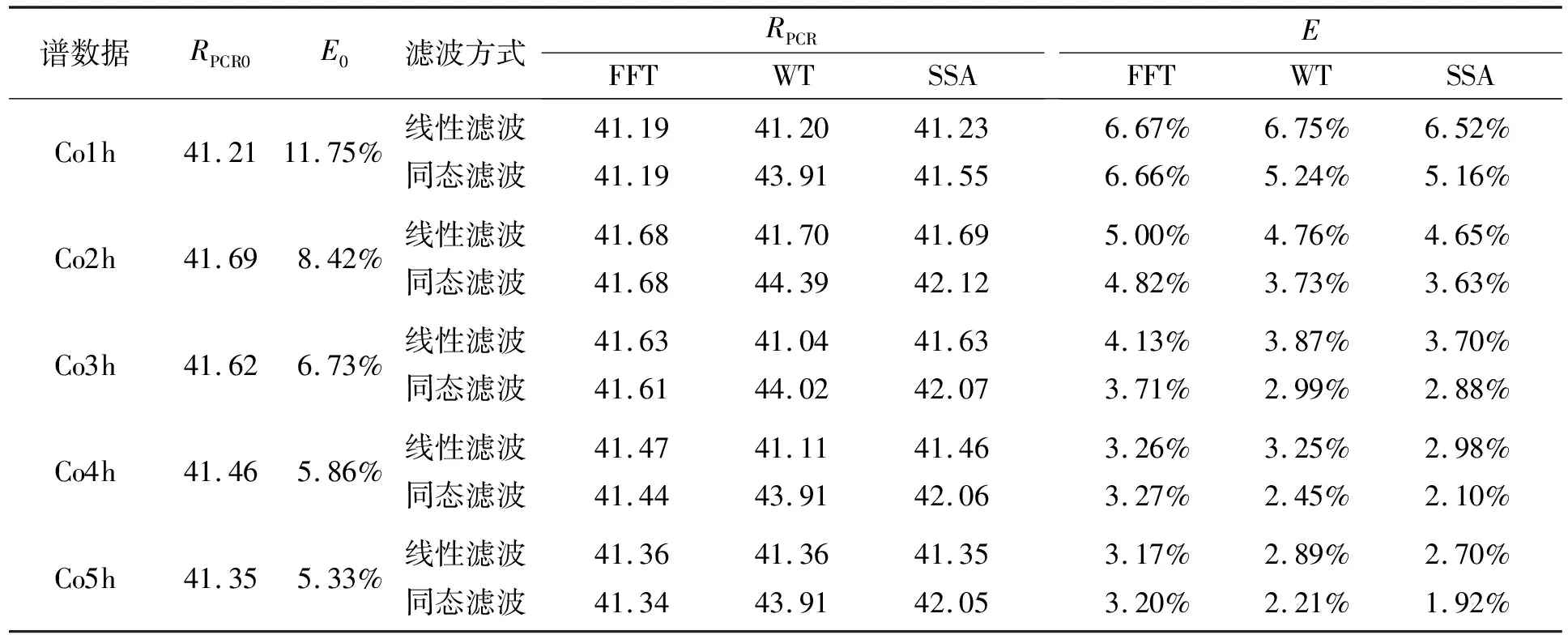
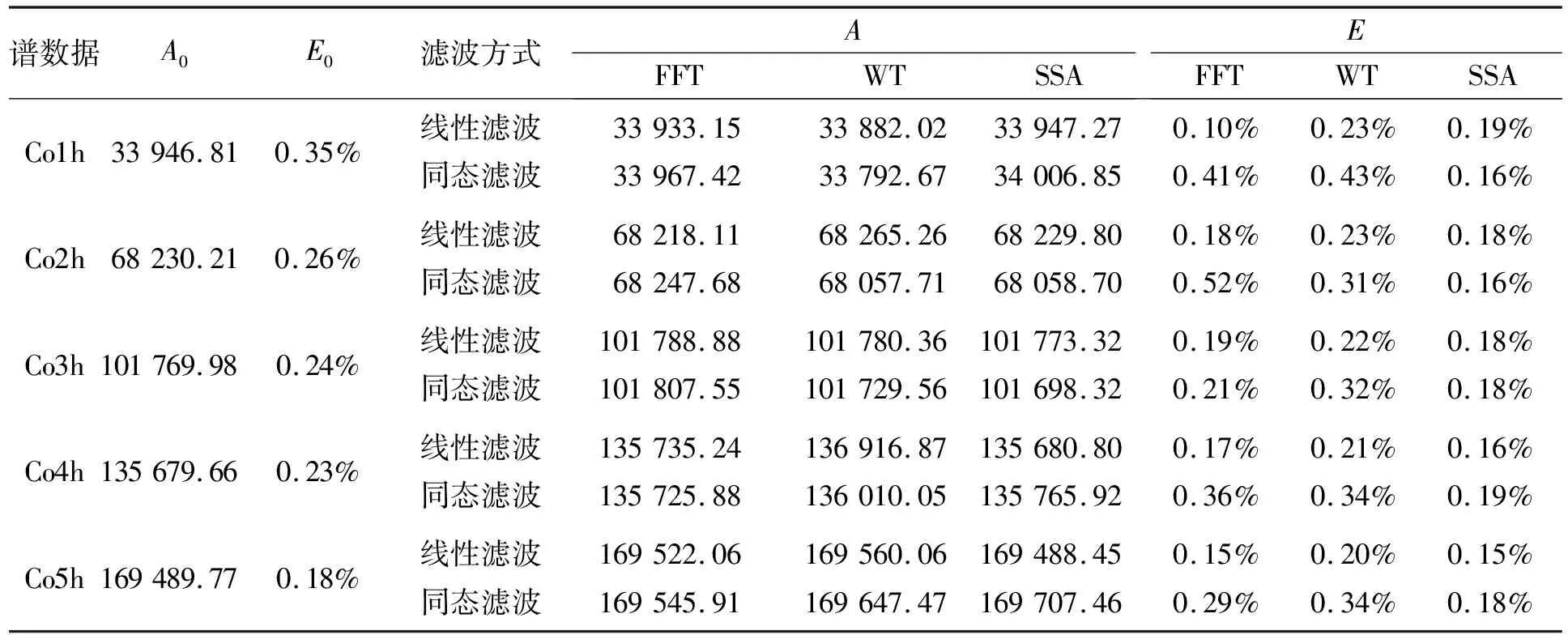
3 结 论

