冲击波位置传感器的电路分析
吕闻龙,徐全余,冯 元,马小娟
(西南交通大学 a.电气工程学院;b.物理科学与技术学院,四川 成都 610031)
扰动冲击波在介质中传播时,由于介质黏性的存在,其能量和动量不断被耗散[1],扰动冲击波的扰动幅度随之减小.基于此思想,可利用波阵面扰动法测量冲击波波阵面的扰动幅度并探究其随传播距离的衰减特点,进而确定材料在高温高压条件下的黏性[2-3].
2005年,刘福生[4]等人为了测量冲击压缩条件下金属材料的等效剪切黏度,设计了便于实验室实施的飞片碰撞扰动实验,即平面飞片碰撞加工有正弦型几何曲面的契形样品,利用离散式电探针技术测量扰动冲击波波阵面在样品中的衰减过程.实验的关键环节是利用与电路相连的电探针记录冲击波到达样品斜面处的时刻,描绘出样品等厚线处扰动冲击波的近似正弦波形,从而获得其演化规律,用于记录冲击波在样品中位置的实验装置称为冲击波位置传感器.
实验中,冲击波位置传感器能否准确测量样品中冲击波传播位置是飞片碰撞扰动法测量材料黏性是否精确的关键.本文利用Matlab中的Simulink模块对实验电路进行设计和仿真,分析影响电压跳点时间精度的因素,为优化电探针测量方法提供了改进依据.
1 冲击波位置传感器测量原理
冲击波位置传感器测量原理如图1所示,左侧固定支架内布置了分别对应样品扰动面的波峰和波谷的5列电探针(图1只画出其中1列),其中每个探针与右侧相应电阻阵列中的电阻相连,对应5列电探针的5个电阻阵列并联接入电容所在的主电路.

图1 冲击波位置传感器测量原理示意图
实验前将样品倾斜测量面与支架贴合,从而保证样品与支架中电探针完美贴合并绝缘.当平面飞片正面撞击样品曲面瞬间,在样品中产生1列右行扰动冲击波.与此同时,触发探针使整个回路被接通,充满电的电容开始放电.由于样品接地,当扰动冲击波传到电探针位置处时,与其串联的电阻瞬间被短路而使得电阻阵列两端的电压瞬间降低,由此记录扰动冲击波到达电探针处的时刻.随着扰动冲击波到达样品的不同厚度处,相应电探针被依次导通,从而使得电阻阵列两端的电压呈阶梯式下降.显然,电压下降沿判读精度越高,冲击波到达样品斜面处的时间越准确.理想的波形具有如下特点:1)电压等高度阶梯式下降;2)下降过程瞬时完成.然而对于实际信号(图2),电压等高度阶梯下降可以由电路设计实现,但由于电路的特点和一些干扰因素会导致电压下降沿不易判读.本文分析了影响电压下降沿弛豫时间的因素,尽量提高电压下降沿判读精度.

图2 电阻阵列电压随时间变化的实验信号
测量电路中电容取值较大(470 μF),放电后(<100 ns)迅速达到稳定电压值,并且可持续足够长时间(>5μs),远大于实际实验时长(<1μs),故可近似为电压源.电容所在主路串联分压电阻RC,每组电阻阵列由10个电阻R1~R10构成(按被短路的先后顺序排序),且在每个阵列尾部串联分压电阻Rfy,所有电阻的阻值选择要满足实验设计要求:随着电探针所连电阻逐个被短路,电阻阵列两端电压呈等高度阶梯式下降.5个电阻阵列中电阻设计完全相同.
2 实验信号分析
图2实验信号的电压下降幅度虽满足等高度下降要求,但在跳点处会经过一定延时才能达到稳定值,且随着各电阻陆续被短路,延时越来越长.这一延时会导致跳点的判断存在较大误差,甚至在多次实验中,后半段的电压跳点几乎难以识别.
2.1 实验电路分析
在任何电路中,都不可避免地存在电抗,阻碍电压电流的变化.本实验中2个电探针被触发的时间间隔很短(约70 ns),微弱的电抗也会起到较大的阻碍作用.实验电路中采用金属膜电阻,本身具有一定的寄生电感LR.同时,电探针通过连接线与电路板相连.由于电探针排列非常密集,故在连接线上会存在一定的电感LS.在电探针导通的瞬间,对应电阻被短路,其寄生电感放电而连接线电感充电,该过程的时间常量为L/R,其中R为电感两端端口网络的等效输入电阻,可近似为电探针对应的电阻[5].而电阻阵列中的电阻值是随电探针导通顺序依次下降,后期被短路的电阻阻值小,时间常量大,放电过程就缓慢.这可以解释图2波形中前半段延时小,而越往后延时越大的现象.
2.2 相对电压下降沿弛豫时间的定义
为了定量地比较不同条件下电路的性能指标,需要量化延时作用的大小.实际测量过程中由于噪声的存在,波形会上下波动,因此本文将电压下降沿定义为放电电压从90%ΔU下降到10%ΔU所经历的时间.两端各预留了10%ΔU的容限,便于比较仿真实验中的下降沿的变化情况.下降沿示意图如图3所示.
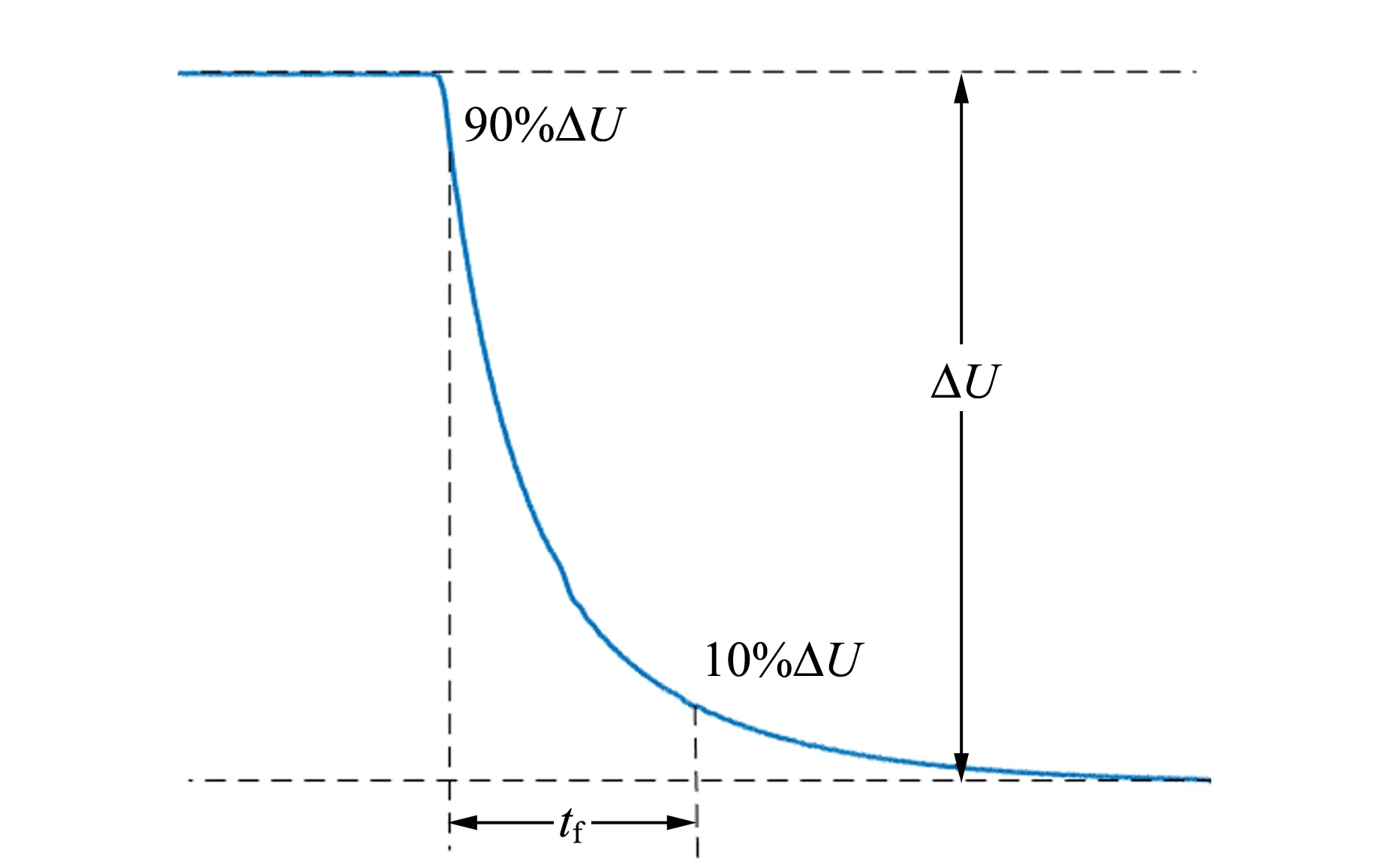
图3 下降沿示意图
相对电压下降沿弛豫时间定义为下降沿弛豫时间占总放电时长的百分比.以第3次电压下降过程为例,是因为前2次电压降通常在较短时间内完成,不同电路的差异不明显;而后半段的电压降有时无法在下一次电探针导通之前完成,导致相对下降沿大于1,但在实验中都作为1来处理,无法达到定量比较电路性能的目的.
3 仿真实验结果与讨论
3.1 Simulink仿真模型的搭建
Simulink是Matlab软件提供的可实现动态系统建模、仿真和综合分析的集成环境[6],可模拟真实传感器工作过程.用Simulink设计的单组电探针与其所连接电路的等效原理如图4所示.

图4 单组电阻阵列电路原理图
图4中电容为470 μF,U为电容充电后的电压.与电阻串联的为电阻寄生电感LR(20 nH),与开关串联的为连接线电感LS(140 nH),其中开关闭合时间由设定好的阶跃信号控制.电缆线及示波器的模型如图5所示,其中电缆线模型为π型网络,特性阻抗为50 Ω,单位长度电容为100 pF,单位长度电阻为0.3 Ω,单位长度绝缘电导为5 μS,电缆线长度为1 m,π型网络的段数为30段.示波器外加50 Ω负载电阻RDL,且其自身也具有一定的电容CDL,大小约为15 pF.
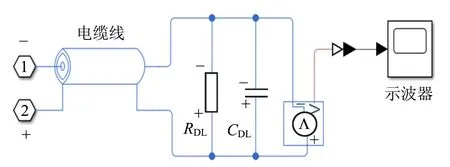
图5 电缆线及示波器仿真模型
运行电路后,示波器显示如图6所示,仿真模型的电信号与实验数据特征基本相符:前期电压下降沿非常陡,后期弛豫时间明显加长,表明所建模型可靠.基于此模型重点分析各因素对电阻阵列电压下降沿的影响.

图6 电阻阵列电压的仿真结果
3.2 电压下降沿影响因素的分析
仿真结果表明,连接线电感、电阻寄生电感、电缆线长度和电阻阵列阻值等因素对电阻阵列电压波形和信号下降沿弛豫时间均有影响,下面对不同因素具体分析.
3.2.1 连接线电感LS
连接线电感主要为自感,其值为
其中,l为导线长度,r为导线半径,μ0为真空磁导率.半径越小,长度越长的导线自感越大.若连接线电缆的电感分别为70,140,200 nH,仿真结果见图7,相对下降沿弛豫时间分别为19.4%,34.8%,47.4%.显然,连接线电感越大,电压下降到稳定值的时间越长,跳点越不易判断.因此,实验中可通过使用更粗更短的连接线,减小连接线电感,减少相对下降沿弛豫时间.
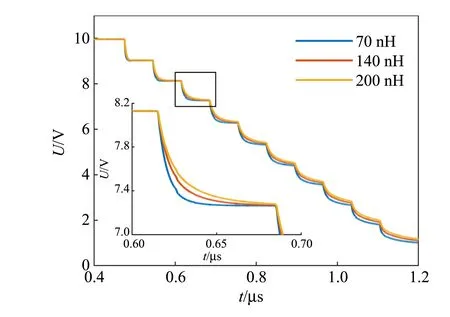
图7 连接线电感对电压下降沿弛豫时间的影响
3.2.2 电阻寄生电感LR
常见电阻有金属膜电阻和贴片电阻,前者内部具有螺旋形结构,存在一定的寄生电感;后者自身结构不会产生电感,故其寄生电感可以忽略.由图8可看出,电阻寄生电感为1,20,45 nH时,相对下降沿弛豫时间为28.8%,33.5%,40.4%.通常贴片电阻体积较小,实验中将金属膜电阻换为贴片电阻,降低电阻寄生电感的同时也可减小电路板的面积,从而减小连接线的长度,间接降低了连接线的电感.
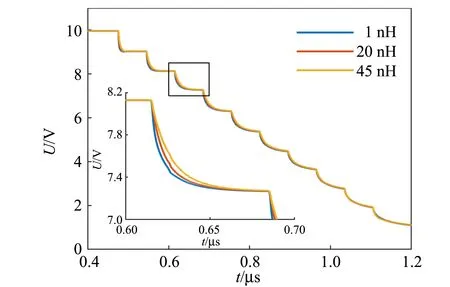
图8 电阻寄生电感对电压下降沿弛豫时间的影响
3.2.3 电缆线长度l
信号在电路中以光速传播,电缆线会对其产生l/c的延时,其中l为电缆线长度,c为光速.飞片扰动实验中,电压单个阶梯下降过程在几十ns的时间内完成,故该延时不可忽略.此外,电缆线的线间电容、电阻、绝缘电导等参量与其长度成正比.由图9可知,电缆线长度分别为1,3,5 m时,电缆线长短对电压相对下降沿弛豫时间为34.4%,35.3%,35.9%.电缆线越长,信号的延时越明显,且电阻阵列的电压值会偏低.电缆线的线间电容约为0.1 nF/m,其值较小,故对信号下降沿的影响可忽略不计.而线间电阻约为0.3 Ω/m,绝缘电导约为5 μS/m,都会因能量耗散对电压值有一定的影响.为使测得的信号更加准确,电缆线长度应尽量减小.飞片扰动实验中5路电阻阵列用于测量样品曲面的波峰或波谷,为得到准确冲击波波阵面形状,5路连接的电缆线长度必须完全一致.

图9 电缆线长度对电压下降沿弛豫时间的影响
3.2.4 电阻阵列阻值R
调整电阻阵列中最小电阻R10的阻值大小(其余电阻的阻值随R10变化,保证电压信号等阶梯下降).电阻阵列对电压信号的影响如图10所示,R10的电阻值较小时,电容放电速度加快,电压信号在稳定时会略微向下倾斜.R10的阻值越小,电阻阵列电压相对下降沿弛豫时间越大,当R10分别取1.8,2.4,3.0 Ω时,电压相对下降沿弛豫时间为54.3%,36.9%,21.5%.因此,在设计电阻阵列时,应尽可能提高最小阻值.

图10 电阻阵列最小电阻值对电压下降沿弛豫时间的影响
3.3 改进方案
综上分析,为使电阻阵列电压跳点判读精度高,即电压下降沿弛豫时间短,针对不同因素对电压的影响总结出如下改进方案:
1)减小电探针连接线长度,以降低连接线电感LS;
2)将实验所用电阻换为贴片电阻,以降低电阻寄生电容,减小PCB面积;
3)各路电缆线长度一致且尽量短;
4)选择合适的电阻阵列且各最小电阻值尽可能大.
设改进后电阻寄生电感为1 nH,并将连接线电感减小至70 nH,电缆线长度减小至0.5 m,在U=50 V条件下电阻阵列各电阻阻值如表1所示.利用上述条件进行仿真,改进后的电压信号中跳点更为清晰,其相对下降沿弛豫时间仅为4.9%.

表1 改进后电阻阵列各电阻的阻值
4 结 论
针对冲击波位置传感器测量得到的电阻阵列电压信号波形存在下降沿弛豫时间较长,判读精度不高的问题,本文搭建了测量电路的Simulink仿真模型,分析了影响电压下降沿弛豫时间的4个主要因素:连接线电感、电阻寄生电感、电缆线长度和电阻阵列阻值设定.其中连接线电感过高和电阻阵列阻值过低是造成电压下降沿弛豫时间延长的关键因素,可通过使用更粗更短的电探针导线及合理设计电阻阵列来对其优化.基于对电路的分析和仿真结果,本文提出了电路改进方案,结果表明该模型下电压跳点更为清晰,能大幅提高判读精度.

