利用静态空气柱测量重力加速度

徐 捷，张 姿，莫凤秀，金三梅，汪 海

(中国地质大学(武汉)数学与物理学院，湖北 武汉 430074)

重力加速度具有重要的研究价值，在探矿、地震预测等方面有广泛的应用[1-3].测量重力加速度有多种传统方法，如平衡法、单摆法、自由落体法等.不同的实验方法有不同的优缺点，比如平衡法误差较大[4]；单摆法容易变成圆锥摆，且摆动周期T与摆角θ的关系不好确定[4-6]；自由落体法测量时，如果使用光电门，由于其自身形状限制，不能很准确测出条形物块下端与光电门的距离[7]；利用悬链摆测量时，为了获得较高的精确度，需要使用精密仪器[8]；利用原子干涉虽然能测出更为准确的数值[9]，但是由于其消耗的人力物力过多，且对实验设备要求过高，因此不适合作为学生实验.上述方法均在动态过程中测量重力加速度，导致测量过程中外界环境引入的误差较大，需要对原理公式进行修正.基于此，本实验方案从新的角度看待该传统研究课题，以静态的过程来测量重力加速度，即通过控制细管中稳定共存的液体柱和空气柱在正立和倒置状态下的压强变化来测量重力加速度.

本实验与其他测量重力加速度的实验相比，只需要测量静止状态的物理量，测量更加方便，且原理易懂、仪器简单、成本低、操作方便.该实验装置获得了“2020年全国大学生物理实验竞赛创新赛一等奖”.

1 实验原理

细管内液柱在静止时，任意一液面的上下压强相等，否则细管内液体会流动；由于毛细现象，在一端封闭的、装有水的细管中，可以存在一段稳定的水柱，如图1所示.

(a)正立 (b)倒置

记图1(a)中状态与图1(b)中状态的空气柱长度分别为h1和h2，体积分别为V1和V2，空气柱和水柱总长分别为h3和h4，压强分别为p1和p2，大气压强为p0，水的密度为ρ.

由玻意耳-马略特定律[5]，有：

p1V1=p2V2,

(1)

又由空气柱的横截面面积相等，则其体积比等于其长度比，有：

(2)

联立式(1)、式(2)可得：

(3)

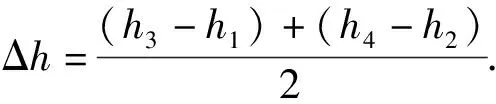
对图1(a)状态，对水柱下液面受力分析：其受到空气柱和水柱向下的压力，以及大气对其向上的压力，水柱处于平衡状态，即两者相等，有：

p1+ρgΔh=p0.

(4)

同理，对于图1(b)状态，下液面受到空气柱向上的压力，以及大气和水柱向下的压力，有：

p2=p0+ρgΔh.

(5)

联立式(3)、式(4)可得：

(6)

将式(5)代入式(6)得：

(7)

(8)

由式(8)可知，在本实验中，重力加速度g与液面高度变化(α和Δh)、大气压强p0以及液体密度ρ有关.

2 实验方法

实验仪器：

铁架台、橡胶塞、蒸馏水、卷尺、细管(细管内径小于10 mm，否则无法形成稳定的液体柱).

实验步骤：

1)将细管的一端塞紧橡胶塞，向内加入适量蒸馏水；轻轻松动橡胶塞，在水柱和橡胶塞之间留出适当长度的空气柱；

2)将细管固定在铁架台上，用刻度尺分别量出空气柱长度h1～h4,测量5次数据取平均值，求得g，并重复5次，部分实验数据如表1所示.

表1 实验数据

武汉地区的重力加速度为9.793 6 m·s-2.图2纵坐标为每组实验中，真实值与实验值之差，可以看出实验值与真实值的误差可以控制在0.3 m·s-2以内.图3中，圆点为每组实验的实验值，误差线为每组实验3倍标准差的值，直线为真实值，可以看到，前4组真实值均落在每组实验值的±3σ之内.5组实验数据中，第2组数据误差最小，为0.09%，第5组数据误差最大，为2.66%，实验数据的不确定度不超过0.05 m·s-2,相对不确定度低.本实验方案不仅理论上可靠，在实际测量中也具有可行性.

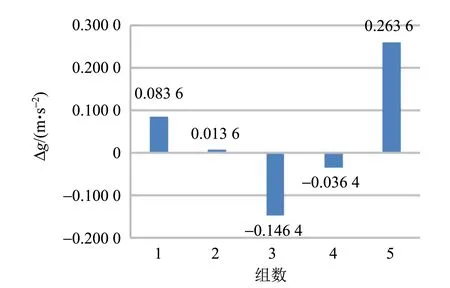
图2 真实值与实验值之差

图3 真实值与实验值的3σ的关系

3 结束语

本文设计了基于空气柱与水柱形成的压强差来测量重力加速度的实验方法和装置，利用该方法测量重力加速度，实验误差小.原理简单易懂，且实验仪器简单、经济，材料易得，不需要借助于物体的运动和计时装置来实现，即测量过程不需要参与物体的运动过程，进而不再需要考虑传统方法中阻力和计时引起的误差.