相干态的海森堡不确定关系验证实验
蒋佳彤,陈 煜,陈 鑫,吴 媛,尹亚玲,陈丽清
(华东师范大学 物理与电子科学学院 物理实验教学中心,上海 200241)
作为支撑现代物理学的基础理论之一,量子力学主要研究微观世界的存在形式和运动规律,在物理前沿问题的研究中不可或缺[1].然而,量子力学内容抽象,数学推导过程繁杂,而且相关实验现象不易在现实生活中直接观测到,导致量子力学在本科教学中仍停留在理论讲授阶段,缺乏生动形象的实验验证帮助学生理解相关理论[2].因此,在本科教学中填补量子实验技术将显得极为迫切.

在量子理论中,量子化光场常用量子正交算符进行表示.量子正交算符包含振幅算符和相位算符,且满足不确定性关系[5].光的量子正交算符在相干态中具有最小不确定关系.相干态是目前最接近经典极限的光场,在量子实验中被广泛使用.本文利用相干光源,结合平衡零拍探测技术,验证了相干态是最小测不准态.该实验研究使本科生在掌握量子物理基本原理及相关实验技术的同时,了解了前沿科学技术发展,提升自身适应现代科学技术高速发展的科学思维能力、创造创新能力和理论联系实际等能力,为创新型人才的培养奠定了基础.
1 海森堡不确定性原理
(1)

下面将根据式(1),通过光场量子化介绍正交算符并验证其不确定关系.
2 量子正交算符不确定关系的验证
光具有波粒二象性,经典哈密顿量表示为[10]
(2)
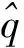
(3)
(4)
(5)
其中
(6)
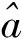
(7)
根据式(5)和式(6)可知:
(8)
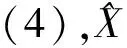
(9)
(10)
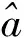
(11)

(12)
由此可见,相干态的正交算符的方差相同,并且满足最小测不准关系,因此图1中曲线上红色圆点即代表相干态,满足式(11)和式(12).

图1 最小测不准态曲线
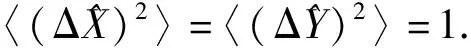
3 量子正交算符的探测
在量子力学中,平衡零拍技术是测量光量子正交算符的重要技术手段.其测量原理见图2.
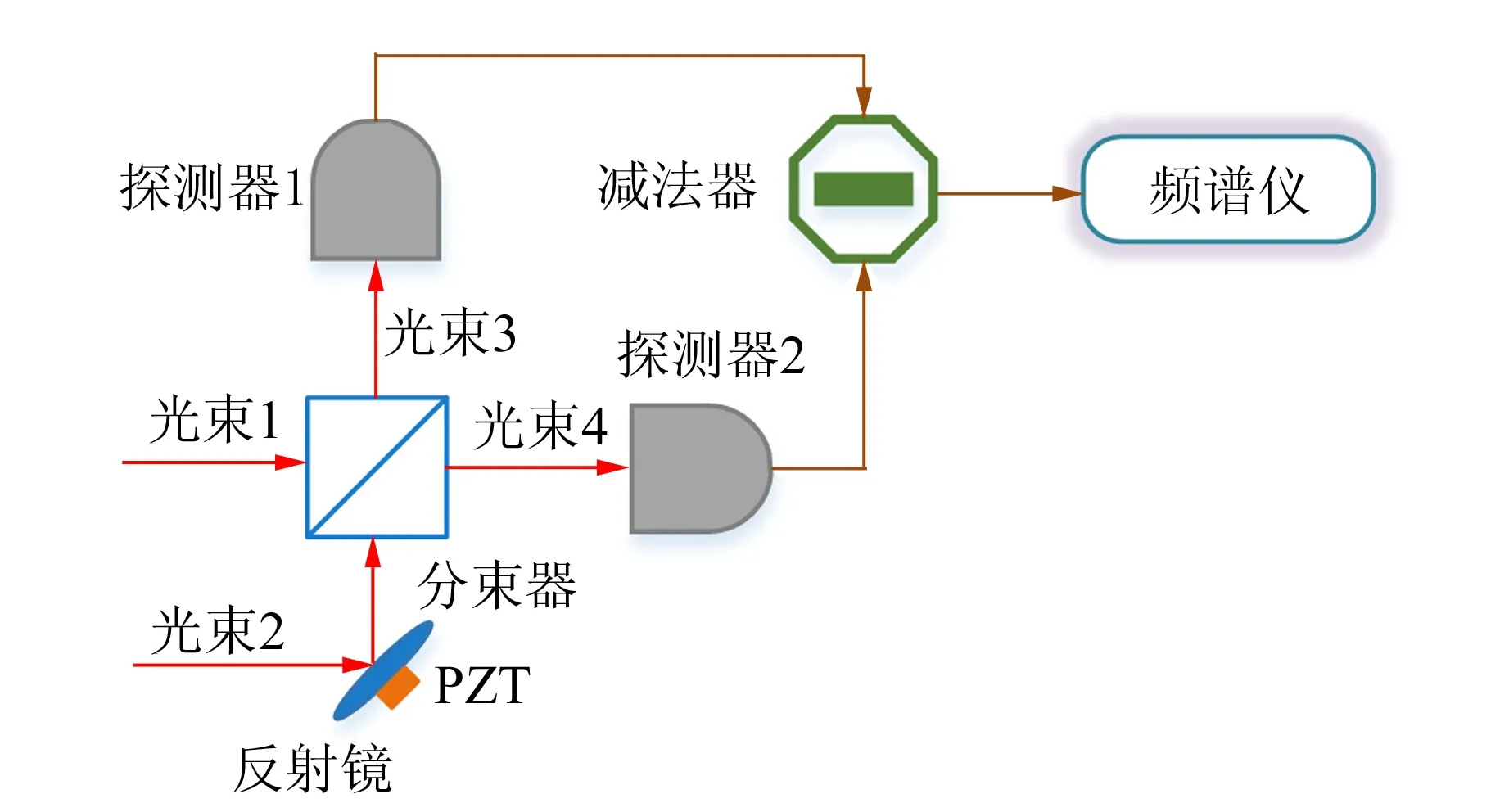
图2 平衡零拍探测技术原理图
具体步骤如下:
(13)
其中,θ是光束1和光束2的相位差.在图2中,反射镜粘贴在压电陶瓷PZT的前端.PZT通过电压控制,可以进行长度伸缩,从而改变θ大小.
2)光束3和光束4分别被探测器1和探测器2探测.假设探测器的量子效率均为100%,即每入射1个光子,光电探测器都相应转化出1个电子,那么光电探测器产生的光电流正比于入射光的强度.当2个光电探测器输出的光电流经减法器相减后,输出的平均光电流〈i〉为
(14)
(15)

3)光电流信号i被输入频谱分析仪,获得i的方差,即
Δ2=〈i2〉-〈i〉2=
(16)
这里|β|2是光束2的光子数,可以通过真空光的平衡零拍探测获得[12].
当θ=0时,可以获得振幅算符的方差,即
(17)
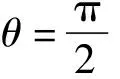
(18)
因此,平衡零拍技术可以实现正交算符的方差测量,从而可以验证正交算符的海森堡不确定关系.
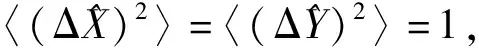
4 实验与讨论
通过以上讨论可知,光场正交算符的方差可通过平衡零拍技术探测,其实验装置如图3所示.
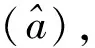
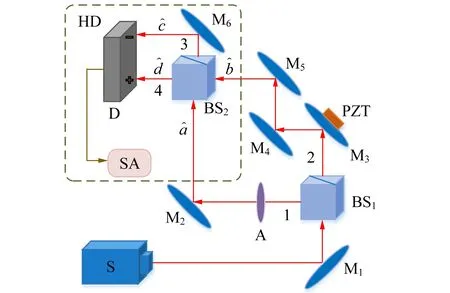
图3 实验装置图
实验过程如下:
1)调节信号发生器发出频率为10 Hz,幅度为10Vpp的三角波,驱动PZT,改变θ.将频谱仪(SA)的探测频率设置为1 MHz,其分辨率带宽和视频带宽分别为3 kHz和30 Hz.
2)将衰减片A的透射率调为0,使光束1无法透过衰减片.此时真空光与本地振荡光进入HD,实现真空光平衡零拍探测,获得其光电流信号的方差Δ2,如图4所示的红色点线.对该方差信号取平均,即可获得|β|2;

图4 当光束1的光强为10.6 μW时,光电流差信号在1 MHz的方差
3)调节衰减片A的透射率,使光束1与光束2的光功率相差100倍.此时相干光与本地振荡光进入HD,实现相干光平衡零拍探测,获得其光电流信号的方差Δ2,如图4所示的黑色实线.

图5 光束1为不同光强时正交算符在1 MHz的方差
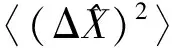

图6 当光束1的光强为10 μW时,正交算符在不同探测频率下的方差
综上所述,光场正交算符在相干态中具有最小不确定关系得到验证.
5 结束语
从光场量子化开始,介绍正交算符并验证其满足海森堡不确定性原理,通过平衡零拍技术探测光场正交算符的方差,从理论和实验上验证了相干态为最小测不准态.该实验将量子力学基础理论通过实验的方式展现出来,直观并形象地展现了微观世界的物理变化规律.本科生搭建实验装置,完成以上实验步骤,可以自主完成基于相干光的海森堡不确定性原理的实验验证.该实验提高学生动手能力的同时,拓展了学生的思路.

