一种融合差分隐私的随机游走算法

华雯丽，黄 刚，唐 震

(南京邮电大学 计算机学院、软件学院、网络空间安全学院，江苏 南京 210023)

0 引 言

近些年，由于移动互联网的兴起，数以亿计的人已经深度接入了互联网。2020年第1季度，全球各大网络社交应用平台用户数量进一步膨胀：推特3.7亿，微信12亿，抖音5.18亿，Facebook 20亿。庞大的社交网络数据，一方面，可以为人们提供越来越符合心意的推荐，Georg Groh和Christian Ehmig的研究[1]表明，在几个真实的推荐系统中，基于社会化推荐系统的用户满意度，明显高于基于协同过滤算法的系统，其最关键的部分是基于好友的选择进行推荐。但是另一方面，个人信息的选择暴露在网络中。用户的个人隐私得不到保障，既会损失用户的利益，也会因此反过来丢失注意隐私的用户。对此，需要设计一些机制，尽量保证数据的隐私性。

针对保护隐私的方法，一般有两种，一种是对匿名方法[2]，但是网络图的特殊性，使得匿名数据遇到节点度数或者结构的攻击，更容易被识别出来，比如，在并不想披露朋友之间的关系的情况下，识别出该独特关系的图数据。另一种算法─差分隐私保护(differential privacy)[3-6]，是由Dwork等提出的新型隐私保护模型，从定义上保证隐私，且与大量的背景知识无关，这种隐私保护算法不仅仅从理论上可以保护隐私，也被用在现实工业应用中[7-10]。

文中的主要工作就是在保证推荐的同时，进行差分隐私操作，保护用户以及好友的个人隐私，主要分为以下几步：

(1)处理用户和物品的二分图，转化成转移矩阵作为数据的输入；

(2)对转移矩阵基于拉普拉斯机制加噪，再进行随机游走；

(3)随机游走得到推荐物品与推荐目标的关联性分值列表；

(4)将每个推荐结果的分值，根据指数机制得到最终的推荐结果。

1 相关概念以及背景知识

1.1 用户行为数据的二分图表示

用户行为有很多种方法可以表示，本节主要讨论用二分图表示用户行为[11]。

由二元组能够表示用户的行为，例如一个二元组(u,i)代表用户u和物品i有行为关系。这些二元组可以直接组成一个二分图。例如，将用户顶点和物品顶点构成一个用户物品二分图，其中顶点之间的边表示用户u对物品i产生的行为。如图1所示，左边表示用户和物品节点，用户A对a,b,d都产生行为，转化成二分图，将A和a,b,d连接起来。

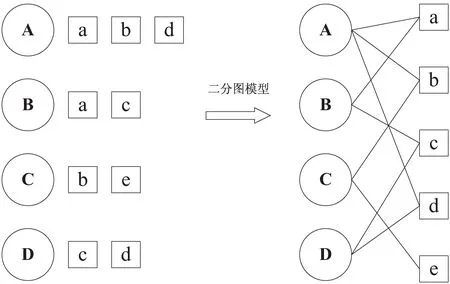
图1 用户与物品之间的二分图

1.2 二分图节点的重要性

得到用户与物品的二分图之后，需要对指定用户进行个性化的推荐，则主要是计算节点之间的相关性，在用户未选择的物品列表中，选择对指定用户节点重要性最高的那个节点，节点重要性越高，对于指定用户节点相关性就越高。

节点之间的重要性比较，第一个重要性是路径个数，指定用户节点到相关的物品节点之间的路径越多，该物品节点对于指定用户节点的重要性越高。举一个例子，如图2所示，假设目标用户是A，A已经连接a,b,d,需要比较c,e两个节点对A节点的重要性，图中左边的二分图中，加粗的线表示A到c有一条路径，长度为3，为(A,a,B,c);图中右边的二分图中，有两组从A到e的路径，长度也为3，为(A,b,C,e)和(A,d,D,e)，相对于c来说，e的重要性更高。

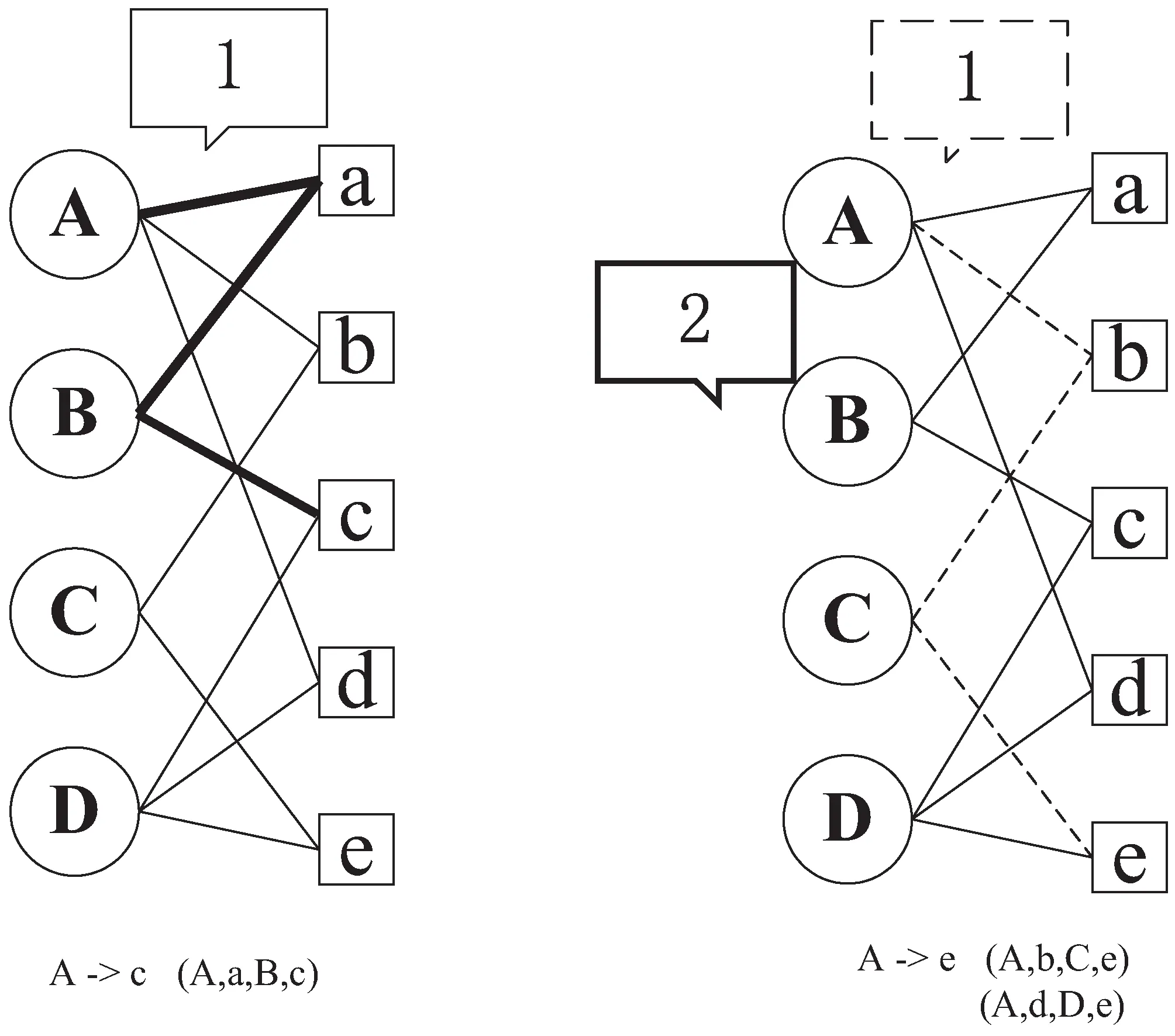
图2 A与a,e之间相关性比较

另外一个重要性比较是从节点之间的路径来看，越分散，重要性越差。如图3所示，从A到e的两条路径，(A,b,C,e)经过的顶点的出度为(3,2,2,2),而另外一条(A,d,D,e)经过的顶点个数为(3,2,3,2),两者比较，(A,d,D,e)经过节点D的出度较大，重要性分散较多。所以，对于节点A到e的重要性而言，路径(A,b,C,e) 比路径(A,d,D,e)的贡献要大。

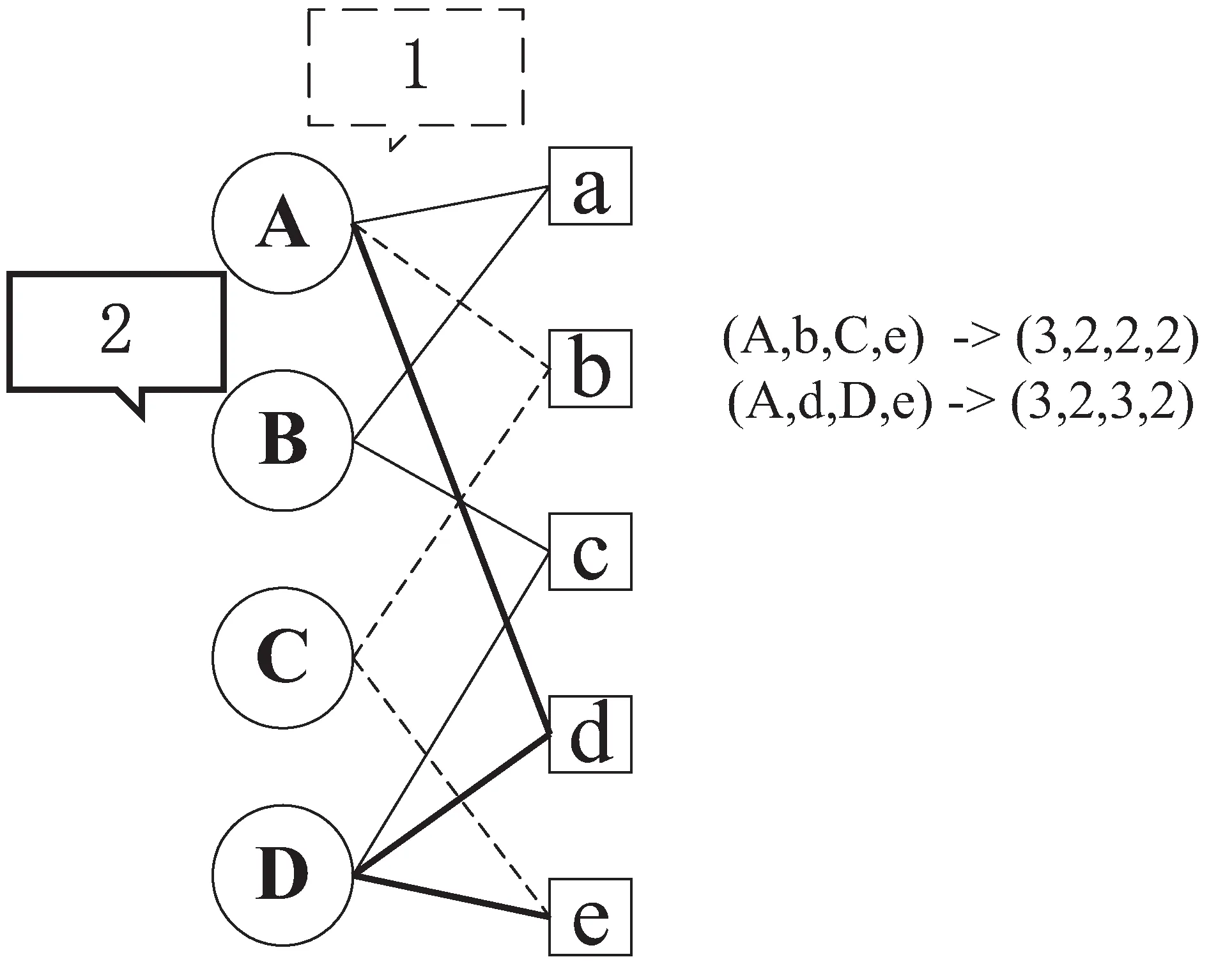
图3 A到e的路径比较

1.3 PageRank

随机游走算法[12]的主要思想来自Google的PageRank，可以计算不同网页之间的重要性，进行排名显示重要性高的节点，该算法的公式如下：

其中，PR(i)是节点i被访问到的概率，∂是用户继续访问节点的概率，N是所有节点的数量，in(i)是所有指向节点i的节点集合，out(j)是节点j指向的其他节点集合。

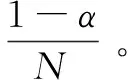
1.4 差分隐私的介绍

差分隐私算法[13-14]在于，向查询输出结果中添加噪声，从而隐藏敏感数据，同时能够保证处理之后的数据，不会影响数据挖掘的结果。假设一个攻击者，有足够大的背景知识的支撑下，就能够从N-1条数据记录中查询做差得到被攻击者的隐私，但是差分隐私能够从定义上解决这个问题。

其核心思想主要体现在两个方面，其一，在插入和删除任意一条数据记录时不会影响输出的结果；其二，无论是否有足够的背景知识，隐私信息也不会泄露。其定义如下：

定义：对于两个数据集D和D'，D和D'相差一条记录，记作|DΔD'|≤1，现有一个随机算法A，range(A)表示该算法的取值范围，如果A在D和D'数据集上输出的结果S，S∈range(A)，符合下面的公式，则称A满足ε-差分隐私。

Pr[A(D)∈S]≤eε×Pr[A(D')∈S]

其中，ε是指隐私保护参数，可以表示隐私保护的程度，该值越小，表示保护的程度越高，Pr[]是隐私被泄露的概率。

(1)敏感度：函数的敏感度可以分为全局敏感度和局部敏感度。这里主要说明全局敏感度，全局敏感度是指对于该函数，在两个D和D'数据集上输出的最大差别，其形式化定义如下：

对于一个任意函数f:D→Rd，d表示函数f的维度，则函数f的Lk全局敏感度Sk(f)为：

其中：数据集D和D'相差一条记录，‖·‖k表示Lk范数。

(2)拉普拉斯机制。

Dwork等人在文献[6]中提出差分隐私保护模型，提出拉普拉斯机制，可以取得差分隐私保护效果，就是通过添加拉普拉斯随机噪声，可以实现差分隐私保护。拉普拉斯分布的概率密度函数为：

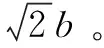
其中，Δf是针对函数f的全局敏感度，ε是差分隐私保护参数。产生的噪声与Δf成正比，与ε成反比。

(3)指数机制。

指数机制的原理是定义一个打分函数q，用来评价每种输出可能性的分值，分值高的输出可能性就会有更高的概率被发布，主要是用于计数统计，例如投票计算。指数机制可以用下面的定义表示。

针对随机算法A，q(D,r)→R，数据集D，输出为一实体对象r∈Range,q(D,r)→R为可用性函数，用来表示输出的可能性。若算法A以正比于eε*q(D,r)/2Δq的概率，从Range中选择并输出r，Δq是函数的敏感度，那么算法M提供ε差分隐私保护。

指数机制的敏感度：S(q)=max‖q(T1,R)-q(T2,r)‖，其中r是任意合法的输出。

差分隐私数据保护框架一般分为以下两种[15]：

(1)交互式保护：用户请求查询数据库，数据库将真实的结果进行差分隐私保护，比如加上噪声，然后将加上噪声的结果返回给用户，如图4所示。

图4 交互式框架

(2)非交互式保护：数据库直接用差分隐私进行保护，形成隐私数据库，直接与用户交互的数据库是隐私数据库，如图5所示。

图5 非交互式框架

文中主要使用的两种融合的交互式保护，先将原始数据转化成转移矩阵，根据拉普拉斯进行加噪，再将加噪的数据作为输入数据，进行PersonalRank排序，得到的结果再根据指数机制进行差分隐私保护。

2 算法设计

2.1 PersonalRank随机游走算法

得到用户物品的二分图之后，对指定用户u进行个性化推荐，就需要在二分图上进行随机游走[13]。启始点为用户节点Vu，以∂的概率决定是不是继续往下走，还是停止，从Vu继续重新开始走。如果是决定往下走，那就从当前节点所连接的节点中随机选择一个节点，作为下次游走的节点，继续重复这样的操作，每个物品节点就会收敛成一个稳定的概率，最后的推荐中，物品的分值就是物品节点的访问概率。以上步骤可以简化为以下公式：

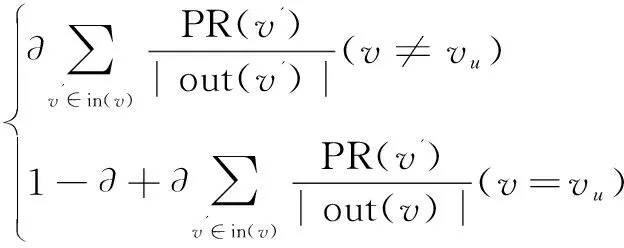
其中，PR(v)表示v的点击概率，就是物品v的分值，out(v')表示物品节点v'的出度，∂表示留在当前的概率。

对比PageRank算法，PersonalRank算法不同点只在于r的值不同，意思便是每次都是从目标用户节点出发，进行随机游走。PageRank是针对所有节点，计算各点的访问概率，而PersonalRank算法是所有物品顶点相对于目标用户节点的概率。

PersonalRank算法虽然能够很好地在物品二分图上进行迭代，但是因为每推荐一次，都要在整个二分图上迭代，直到整个二分图的概率稳定，使得这个过程时间复杂度较高，生成的推荐结果很耗时，同时也无法在线提供实时推荐。

为了解决整个问题，有两种方法，第一种是控制迭代的次数，设定一个指定迭代次数，在收敛之前就可以停止。但是这种方法有个问题，准确度无法保证，但是影响不大。另一种是转化成矩阵计算，将二分图转化成转移矩阵的形式，公式如下：

或者写成：

将v转移为v'，得到的是一个概率值，|out(v)|是v的出度，是一个实数，那么1/|out(v)|就可以表示这个节点v转移以后的概率矩阵。

那么，迭代公式可以转化为：

r=(1-∂)r0+∂MTr

解方程得到：

r=(1-∂MT)-1(1-∂)r0

因为只看相对的大小，而取r中元素排序的前k个值，则忽略1-∂的具体值，只要计算(1-∂MT)-1的值，并且该式是高度稀疏矩阵，容易计算。

举个例子来说，如图6所示，将二分图转换成转移矩阵，每一列表示一个节点出边的权重，例如第一列表示节点A的出边，它对a,c两个节点分别有一条边，权重为1/2，所以该图对应的转移矩阵如下：

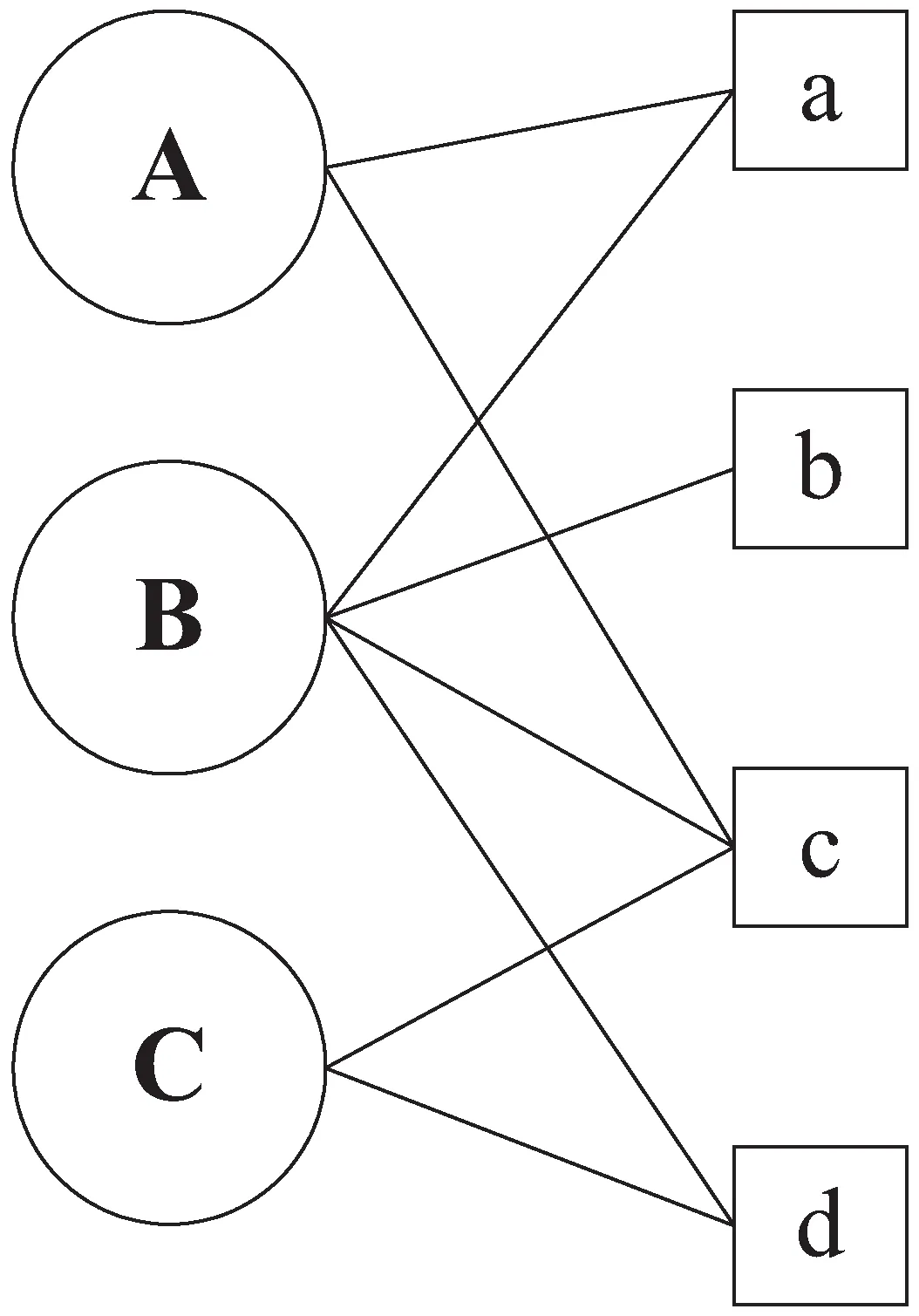
图6 二分图

第一行是各个节点转移到节点A的概率，而r的第一列分别是各个节点当前的PR值，因此用M的第一行乘以r的第一列，所得结果就是节点A的最新PR值。

2.2 融合差分隐私的模型计算

为满足差分隐私，先将数据集处理，针对二分图转化成转移矩阵，计算对应点的PR值，加入拉普拉斯噪声，进行PersonalRank随机游走，根据得到的每个物品节点的分值，筛去目标用户已经做出选择的物品。由于物品数量很多，推荐结果只需要一个，可以将得到的物品分值取出Top10，以这10个物品的分值作为打分函数，以满足指数机制的概率输出一个目标物品。图7是整体的流程图。

图7 融合差分隐私流程

输入：用户物品评分和目标用户u；

输出：输出给目标用户的推荐物品item。

(1)处理输入数据，转化成二分图模型；

(2)计算转移矩阵，加上拉普拉斯噪声；

(3)根据PersonalRank的公式计算每个节点PR分值;

3 实验与分析

3.1 数据集

根据以上提出的计算方法，本节将在真实数据集上进行实验，用来验证新算法。实验结果表示不但可以进行差分隐私保护，同时也能达到一定的推荐准确率。

数据集是ratings15000.csv，截取自MovieLens数据集，来自http://grouplens.org /datasets/movielens/，主要结构如表1所示。

表1 数据集结构

3.2 实验结果

实验默认迭代次数iter_num为100次，只要满足迭代条件，迭代停止。图8是iter_num 随α变化而变化的折线图，这里取0.8，比较符合实际。

图8 iter_num 随α变化而变化的折线图

另一个主要的参数是隐私保护参数ε，由文献[16]可知隐私预算ε越大，数据可用性越高，安全性越低，当隐私预算ε=0时，数据失去意义。

该实验得到的结果，主要是以节点分值为打分函数，以指数概率输出，每次得到推荐物品并不一定相同，以下图标是统计分值前十的物品，在100次查询中，不同的隐私预算的情况被输出的次数(见图9)。

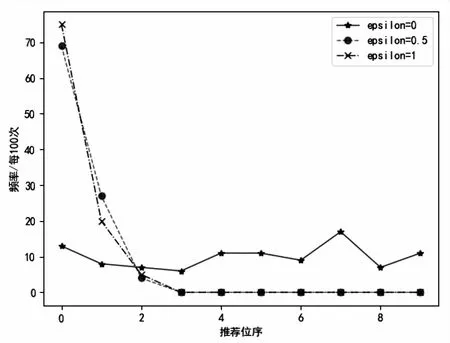
图9 推荐位序前十物品每次输出频率

由图9可以得知，该模型能够很好地保护输出的结果，高概率的分值以指数高概率输出，低概率的分值以指数低概率输出，每次查询的结果并不一定相同，同时，由于是取的分值前十，也在一定程度上保证了推荐的准确度，同时也验证了隐私预算越大，数据可用性越高。

4 结束语

为了保证推荐结果的隐私性，通过差分隐私的拉普拉斯机制和指数机制，以PersonalRank都得到的分值，敏感度为最大分值减去最小分值，筛选目标用户选择的物品，取Top10为打分函数，以满足差分隐私的概率输出推荐物品。该模型每次输出的推荐结果不一定相同，分值高的节点输出概率更高，因为满足指数机制，可以保证攻击者不会通过查询作差得到目标用户或者其他用户对物品的行为。但是该模型针对大型网络图数据迭代时间复杂度过高，应用中需要根据实际情况选择。