应用同伦群计算表示复杂拓扑闭曲面的方形图

蒙毅琦，张家玲，杨彦敏

（昆明理工大学 理学院，云南 昆明 650500）

0 引言

在图论与几何学中，运用几何体表示图的组合结构是研究热点之一。例如较为常见的平面图圆周接触表示，此时一个平面图都用一组相切的圆周来表示，图中每个顶点被一个圆周代替，而连接两点的一条边则由两个圆周相切的关系进行描述［1］。这种几何表示的意义在于将图的组合结构与几何结构联系起来。随后学者们进一步研究图的矩形接触，哪种类型的图具有这种几何表示，如果有，如何生成它们。事实上，图的几何表示问题可转化为图上的算法问题。例如图绘制工作中对平面图矩形表示的讨论，对于边仅在端点处相交的平面图，在被视为矩形剖分的骨架下具有该图的矩形表示［2］。一部分学者研究具有矩形表示的图结构特征及实施算法，其认为如果目标图对偶于一个平面图，且平面图具有一个矩形表示，则目标图也具有矩形表示［3-4］。

在代数拓扑学中，颇受关注的热点之一就是拓扑空间的同伦群研究，并产生了丰富的研究成果。同伦群研究不仅在代数拓扑学中十分重要，在其他领域也有着广泛应用。近几十年来，计算同伦理论一直是研究热点，其在相关领域的应用也催生出新的研究问题，如拓扑组合学中同调论的算法问题。部分研究小组重点考虑同伦理论的有效算法［5-8］，并为计算实施设计了有效框架。也有部分研究工作着力于分析相关计算的复杂性，或对其进行较为全面的总结［9-14］。

1 相关研究

将一个拓扑空间X的同伦群πd(M)定义为从d维球面到M连续映射的等价类，同伦群元素可利用生成元和关系表示为抽象群。同伦群计算通常基于拓扑空间的CW胞腔分解，组合算法源于Seifert -Van Kampen 理论。由于同伦群与同调群密切相关，在某些情况下，同伦群生成元计算也适用于同调群生成元计算。同调群提供了一种测量拓扑空间中d维洞的数学方法，计算同调理论在计算机科学领域引起了广泛关注。由于同伦群与同调群为几何对象，所以其都可借助计算机进行可视化。同调群的生成元可直接由同伦群的生成元获得，例如对于定向闭曲面的胞腔分解，存在最小同伦群与同调群生成元计算算法［15-16］。对于图棱锥的情况，已有研究讨论了计算2 连通、3 连通单纯复形同调群生成元的算法框架［17］。作为同调群的对偶，上同调群比上述群更微妙，但在拓扑上也更为有用。通过一种链式构造的概念，可给出上同调群生成元的计算算法，如计算二维情形的上同调生成元，已在图像处理、图像识别等领域取得了一定研究成果［18-22］。上同调类有一个调和形式的特殊表示。根据Hodge 理论，微分形式空间可分解为外微分算子及其共轭算子的像以及Hodge -laplace 算子核的直和。Hodge -laplace 算子核可作为上同调类的特殊表示，即调和形式。近年来调和形式被应用于辅助机器人进行网络规划与分类［23-24］、数据分析［25］及秩序安排［26］等方面的工作。调和1-形式还可用于计算网格上的平直度量［27-28］，事实上这就是一个网格参数化过程。调和1-形式及其共轭形式可生成全纯1-形式，从而促进了全局共形参数化方法的产生［29］。

本文首先应用同伦群生成元切割闭合曲面，以简化曲面拓扑结构，然后计算以调和1-形式表示的上同调群生成元，并进一步以调和1-形式沿着边的积分给出图的方形表示。由于同伦群生成元适用于任何闭曲面，因此该方法的优点是适用于处理具有复杂拓扑结构的图。

2 方法介绍

2.1 理论基础

定义1（同伦群）给定基点p∈M，连续映射f:[0,1] →M，且f(0)=f(1)=p称为一个环路。对于f(1)=g(0)的两个回路f、g，其乘积表示为：

如果两个环路f、g可连续变形为另一个环路，则称这两个环路同伦等价，两个环路的串联构成了其在群中的乘积。具有公共基点p的环路等价类集合形成一个群，称为一阶同伦群或基本群，表示为π(M,p)。在不同基点上定义的群是同构的。

用一个共同基点与环路之间的组合关系定义基本群，这是一种标准的组合方式。对于组合曲面，即一个具有图结构且每个面都被边包围的二维流形是一个拓扑圆盘，Eppstein［15］提供了计算组合曲面基本群生成元的算法。

显然，二维流形上的单纯复形也是一个以图为1-骨架的组合曲面。因此，单纯复形上同调群的定义可被自然地应用于组合曲面。

令Mi为组合曲面M的i维元素集，其中Mi(i=0,1,2)分别表示顶点集、边集和面集。如果将组合曲面视为单纯复形，则顶点、边、面分别为0 -单纯形、1-单纯形和2 -单纯形。将σi表示为i-单纯形，线性组合∑jλj σj(λj∈Z)被称为i阶链。

i阶链的集合被称为i阶链群Ci(M)。i阶边界算子定义为同态∂i:Ci(M) →Ci-1(M)，i阶闭合链群定义为∂iσ=0 的i阶链集，i阶边界链群定义为∂iσ=γ。其 中，σ∈Ci(M),γ∈Ci+1(M)的i阶链集。用ker∂i、img∂i+1分别表示i阶链群与i阶边界链群，i阶同调群是商群。

定义2（同调群）i阶同调群定义为：

Hi(M)中的每个元素都是一个i维同调类。

从流形的庞加莱对偶来看，组合曲面M有一个对偶组合曲面，其中面f∈M的重心对应于顶点，边e=fi⋂fj∈M有一条对偶边，其两个端点为从对偶观点来看，i阶链群Ci(M)有一个对偶群，称为i阶上链群，表示为Ci(M)。实际上，Ci(M)是从Ci(M)到系数群的映射群。i维上边界算子di:Ci(M) →Ci+1(M)定义为dω(σ)=ω(∂σ)，其 中σ∈Ci+1(M),ω∈Ci(M) 且dω∈Ci+1(M)。i阶闭上链群定义为满足条件di ω=0 的i阶上链群。i阶上边界链群也称为i阶恰当上链群，定义为满足条件ω=diτ的i阶上链群，其中ω∈Ci(M),τ∈Ci-1(M)。分别用kerdi、imgdi-1表示i阶上链群Ci(M)与i阶恰当上链群Ci(M)，i阶上同调群是商群。

定义3（上同调群）i阶上同调群定义为：

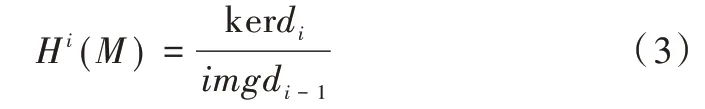
Hodge 理论提出了空间的分解，并给出每个上同调类的最优表示。σi+1:Ci+1(M) →Ci(M) 定义为其中ω∈Ci(M),η∈Ci+1(M)，σi+1是di的伴随。Hodge LaplacianΔi可被定义为Δi=σi+1di+di-1σi。Δi:Ci(M) →Ci(M)是自伴算子，也是半正定算子，因为对于Hodge定理证明了任意i阶微分形式可分解为di-1、σi+1的像与Δi核的直和，Δ i的核记为微分调和群同构于微分上同调群。

定理1（Hodge 分解）对于Ci(M)中的任何形式，都存在唯一的分解公式：

2.2 相关算法

下面主要考虑组合曲面M=(X,G)，其中G是嵌入到二维流形X上的加权图，嵌入的每个面都是拓扑圆盘。图G=(V,E)传统上是一对顶点集V与边集E的组合，G有相应的对偶，其中G上的一个顶点对应于上的一个面，如果两个对偶顶点对应的原始面共享G中的一条边，则上的对偶边放置在两个对偶顶点之间。Eppstein 算法给出了组合曲面一阶同伦群生成元的产生过程。

算法1 Eppstein 算法（一阶同伦群或同调群的生成元）T是G的一个生成树；

对于一条边e∈E，假定γ(e)表示T⋃e中的唯一环路，环路集{γ(e)|e∈E}建立M一阶同伦群的一个基底。

图1 显示了一组同伦群基底。用于表示基本群基底的环路集合也是一阶同伦群基底，这是Hurewicz定理的结果，反之则不成立，更多细节可参见文献［16］。

Fig.1 A set of homotopy group basis for a genus 2 surface图1 2 亏格曲面的一组同伦群基底

曲面的一阶同伦群生成元集合也是其割图的同伦群生成元集合。将封闭曲面沿其割图割开，可得到圆盘型曲面，从而简化曲面的拓扑复杂度。因此，一些平面算法可推广到非平面曲面。2 亏格曲面切割图如图2 所示。

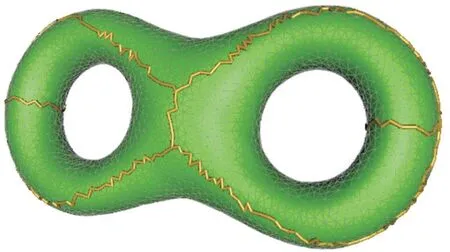
Fig.2 A cut graph of a genus 2 surface图2 2 亏格曲面切割图

上同调群比较抽象，但易于计算实现，其计算过程可转化为线性代数问题。根据Hodge理论，调和1-形式是每个上同调类的最优表示，并可在曲面上进行可视化。根据算法2，可通过纹理映射可视化调和1-形式群的一组基底，如图3 所示。通过使用Hodge星算子，调和1-形式可生成其对应的共轭1-形式。考虑在共轭调和1-形式的曲面上将每个调和1-形式旋转90°，该方法可通过相应向量场上的内积来实现。将调和1-形式及其共轭的1-形式进行合成，可生成曲面上的全纯1-形式。选取最佳全纯1-形式群中的表示元，将曲面的全局共形参数化［30］，如图4 所示。

Fig.3 A set of basis of harmonic 1 form group for a genus 2 surface图3 2 亏格曲面调和1-形式群的一组基底

Fig.4 A visualization of conformal parameterization on a genus 2 surface图4 2 亏格曲面上共形参数化的可视化

算法2Gu与Yau算法（调和1-形式基底）

令{ω1,ω2,…,ω2g}是g亏格曲面M的一组一阶上同调群基底；

对于任意ωi，找到一个泛函fi:M→R，使得ωi+dfi满足Hodge laplacian方程；

{ω1+df1,ω2+df2,…,ω2g+df2g}是调和1-形式群的一组基底。

3 实验结果与讨论

3.1 算法实验

算法3 闭合曲面的方形图算法

2 亏格闭合甜甜圈曲面的方形图表示如图5 所示。

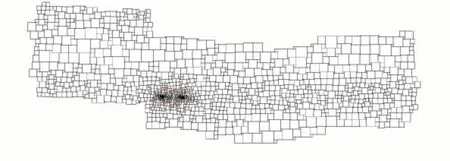
Fig.5 The square drawing representative of a closed genus 2 surface图5 2 亏格封闭曲面方形图表示

一个组合调和1-形式ω可在平面上诱导一个表示图G的方形图，也把一个平直度量赋予具有奇异点的图G及其嵌入面S，ω的零点是方形退化的奇异点。根据Riemann-Roch理论，一个g亏格曲面共有2g-2 个奇异点。在图5中，2 亏格甜甜圈曲面的奇异点由两个红色圆圈进行标记。根据文献［29］，每个顶点v∈V的拉伸因子为：

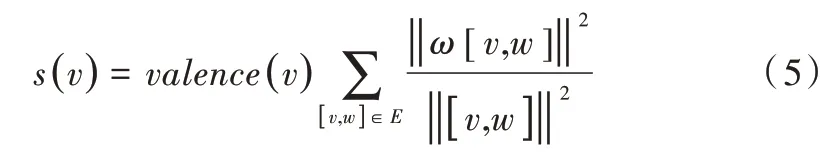
s(v)的最小顶点近似于ω的零点位置。

给定G上的1-形式ω，对于每个顶点vi，如果分配一个+号，否则分配一个-号。遍历vi的所有环绕边，观察符号变化次数，vi的指标为：

类似地，对于每个面f=[v0,v1,…vk] 以及一条边如果则分配一个+号，否则分配一个-号。遍历f的所有环绕边，观察符号变化次数，f的指标为：

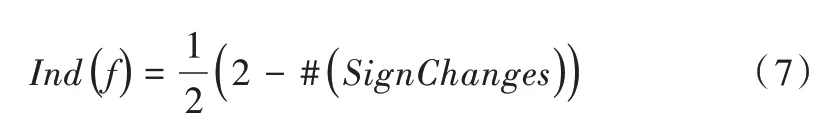
如果Ind(v)不等于0，则顶点v是分支顶点。类似地，具有非零指标的面是分支面。顶点与面的总指标为：

式中，χ(G)=2g-2 为G嵌入面的欧拉数。

然而，以上过程仍然存在一些局限性。尽管有一些处理零点的方法，但在给定组合曲面的几何表示中不希望存在零点，本文希望避免表示边的方形退化。目前，这种限制无法改变，因为所提出的方法是从代数拓扑推导而来的，其中一些结果是由给定对象的拓扑信息决定的。

3.2 算法分析

为测试本文所实施算法（算法3）的稳定性，计算不同尺度大小与亏格数曲面的方形表示结果。实验结果如表1所示。

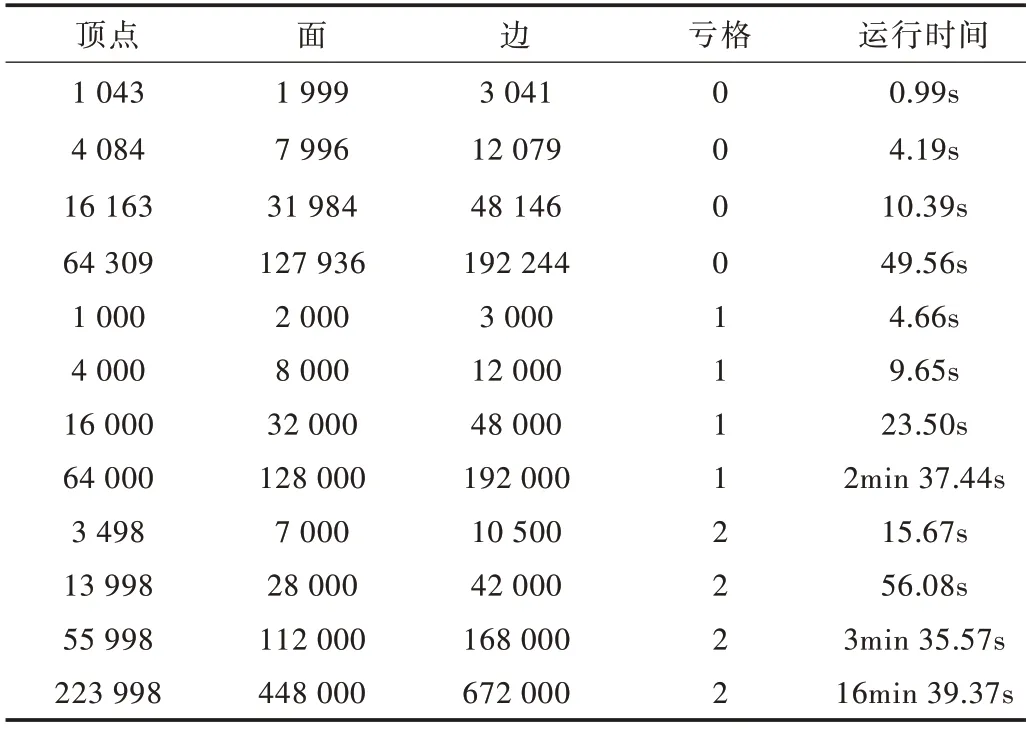
Table 1 The square drawing representative of different surfaces表1 不同曲面方形表示

分析表1 可得出计算的时间复杂度取决于亏格数g与顶点数n。曲面拓扑结构简单，需要运行的数据较少，因此运算速度较快。如表1 的前4 项，对于亏格数为0 的曲面，若顶点数翻4 倍，计算运行时间也会相应翻4 倍；对于亏格数为1 的曲面，在接近的顶点数下，当顶点数成倍发生变化时，运行时间消耗更多，且运行时间与顶点数之间不具备明显的倍数变化关系；对于亏格数为2 的曲面，在相近的数据下，运行时间变化巨大。由以上实验结果可分析得出算法的时间复杂度相对应于曲面亏格数g与顶点数n都是非线性的，而其是否具有指数复杂度，有待从理论上对算法进行分析与证明，因此需要更多理论工作的支持，期望后续在理论分析方面能有所突破。

4 结语

本文介绍了具有复杂拓扑结构的封闭组合曲面的方形表示，该方法基于同伦群生成元的计算，曲面的一阶同伦群生成元集合也是其割图的同伦群生成元集合。沿着封闭曲面的切割图切割曲面，可简化曲面的拓扑复杂度。因此，同伦群计算为将平面与曲面的某些算法应用于封闭曲面提供了有力工具。受此启发，本文提出计算封闭组合曲面方形表示的算法。该过程首先应用同伦群生成元切割封闭的组合曲面，并计算其调和1-形式作为上同调群生成元的表示，然后通过沿边的调和1-形式积分确定方形边长，最后在不同曲面上测试算法的稳定性。由于本文方法源于拓扑学，根据Riemann -Roch 理论，几何表示中存在一定的方形退化情形，即存在奇异点，因此后续工作将主要着力于对异议点的控制，以尽可能保持曲面更多的几何信息。