一种基于机械式拼接的结构光扫描测量方法

武 琼，刘 巍，周志龙，王钰鑫，乐 毅

（1.大连理工大学 机械工程学院，辽宁 大连 116033；2.北京卫星制造厂有限公司，北京 100080）

引言

在航空航天装备制造中，广泛存在大量具有复杂几何形貌的支架构件。这些支架上通常有多个较小的特征形面，特征形面之间的位置尺寸需满足一定的精度要求，以保证整体部件的最终制造精度[1]。扫描测量方法具有速度快、非接触、操作灵活等优点[2-3]，可实现复杂结构零部件的形面测量，为加工过程中被测物体的几何尺寸获取与形状精度的评估提供了数据支撑。

局部高精点云扫描方法，从设备上可分为线激光扫描[4-5]、单目结构光[6]和双目结构光等方法[7-8]；从原理上可分为激光三角法、相位轮廓术等方法。由于测量精度与范围的矛盾性，扫描精度优于50 μm的视觉扫描传感器，其单次测量视场约为50 mm，难以直接实现超过100 mm的零件面形高精度测量。目前主要采用全局基准拼接、公共区域顺序拼接及机械式拼接等拼接方法[9-12]实现较大尺寸的零件面形测量。其中全局基准拼接法依赖全局大尺寸测量传感器测量端扫描机构的全局位姿，一般需要如i-GPS[13]或者激光跟踪仪等设备，典型代表为Leica公司的T-Scan扫描仪，其组成复杂，价格昂贵；公共区域顺序拼接法需要公共区域的突出特征或靶点作为拼接依据，存在“测量蛙跳”现象,导致拼接过程中会产生误差累积,测量精度难以保障；而采用高精度运动执行机构,将局部高精点云数据进行拼接，这种方法转换链简单，拼接精度高。尽管较大行程的高精度运动执行机构价格昂贵，但设备综合成本仍远低于全局基准拼接方法所需要的大尺寸测量传感器；与公共区域顺序拼接法相比，该方法无需使用复杂的坐标系转换算法，所以这种方法适用于支架结构上多栓接结合面的形位公差测量。天津大学的尹世斌[14]和大连理工大学的张仁伟[15]均采用了单轴平移台和线激光扫描进行组合式测量的方法。但由于机械运动机构与扫描仪器缺少实物基准，两者的坐标系难以精准统一，严重影响测量拼接精度，难以实现较大范围内的复杂面形高精度测量。

本文提出了一种基于机械式拼接的结构光扫描测量方法，通过高定位精度的十字平移台，将不同位置下结构光扫描仪的拍摄数据拼接，最终实现了对复杂形貌零部件的测量。根据系统的组成和测量原理，基于距离约束、几何约束和非线性优化方法，建立测量系统标定模型；最后通过实验对系统进行标定，并通过球心距验证系统拼接精度，最后对适用性进行了验证。

1 系统组成与测量原理

1.1 系统组成

采用十字平移台与结构光扫描仪搭建拼接式测量系统，如图1 所示。十字平移台由2台高精度单轴平移台组成，分别操控十字平移台的2个轴，改变结构光扫描仪的拍摄位置；将待测物体固定于升降台上，通过改变机械臂末端位姿，以调节升降台的位置和姿态，从而确保物体的待测区域位于系统可测量范围内；测量过程中保证机械臂位姿不变，从而确保测量过程的稳定性。

图1 拼接式测量系统Fig.1 Splicing measurement system

1.2 测量原理

对于高定位精度、高运动精度的单轴平移台，其运动过程可视为平移，旋转忽略不计。X轴平移台与Y轴平移台分别只沿着轴L1、 轴L2平移。由于结构光扫描仪内部结构以及安装过程中装配工艺、夹具制造等问题，轴L1与 轴L2无法确保垂直；轴L1必 然与扫描仪测量坐标系OMXMYMZM中的轴ym、ym、zm存在夹角 α1、 θ1、 β1， 轴L2必然与扫描仪测量坐标系OMXMYMZM中的3个轴存在夹角 α2、 θ2、 β2。这6个夹角的余弦值，也就是需求解的外参，即X1=[cosα1cosθ1cosβ1]T，X2=[cosα2cosθ2cosβ2]T。系统坐标系的变换如图2所示，图中L1、L2表示单轴平移台的运动方向；OMXMYMZM表示测量坐标系的初始位置；OMIXMIYMIZMI与OMIIXMIIYMIIZMII分 别表示结构光扫描仪沿X轴平移台和Y轴平移台平移后 的测量坐标系。

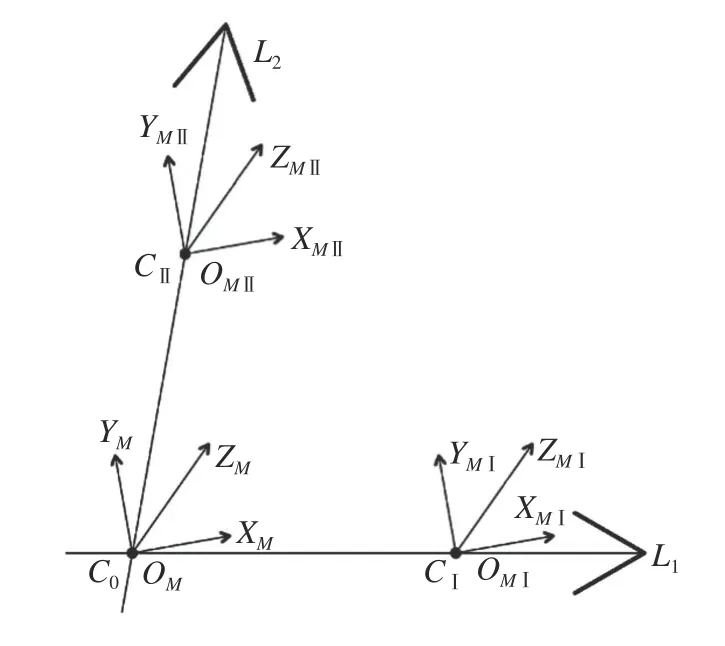
图2 扫描仪测量坐标系变换示意图Fig.2 Scanner measurement coordinates transformation

欧式空间刚体变换可表示为p′=Rp+t，其中R为一个表示旋转的3×3阶矩阵；而t为一个表示平移的3×1阶矩阵。结构光扫描仪在十字平移台上i处位置 (CIi,CIIi)测 得一点其中下角标中罗马字母I与II分别表示X轴与Y轴平移台；数字1与字母i、j均表示拍摄位置序号（下同），则此点相对于j处位置的坐标描述为

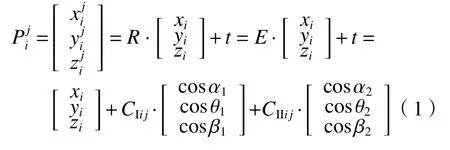
式中：CIij=CIi−CIj；从上文可知，扫描仪沿着十字导轨运动，旋转可忽略不计，所以可认为R=E;而t是一个与运动距离和外参都有关的量。由此，可以将不同位置下的测量数据统一到同一坐标系下。所以，实现基于机械式拼接的结构光扫描测量方法的关键，就在于6个外参的求解。

2 机械式拼接扫描测量系统参数标定

本章将提出一种测量系统外参标定方法。扫描仪测量坐标系在平移过程中，每个轴的方向不会发生变化。利用这一条件，分别求解平移台2轴的外参。对于其中一轴，通过标定靶尺上靶球的球心距建立距离约束，结合参数自带的几何约束，建立具有权因子的目标函数；最后通过非线性优化的方法求解函数极值，得到参数最优解。以X轴外参求解过程为例，具体过程如下。

操控X轴平移台，将扫描仪移动到不同的位置，记录坐标值CI1、CI2…CIn，每次拍摄靶尺上不同靶球。从深度图还原点云信息，通过最小二乘法，提取每个位置对应的靶球球心相对于测量坐标系的坐标 (XI1、YI1、ZI1)， (XI2、YI2、ZI2)… (XIn、YIn、ZIn)。

若位置CIi下拍摄的球心坐标为 (XIi、YIi、ZIi)，位置CIj下拍摄的球心坐标为n)， 那么i球球心坐标PIi与j球球心坐标PIj的距离可表示为

式中：CIij=CIi−CIj，XIij=XIi−XIj，YIij=YIi−YIj，ZIij=ZIi−ZIj。

应与经过三坐标测量机检定过的i球、j球球心距Lij相 等，由此建立距离约束，即

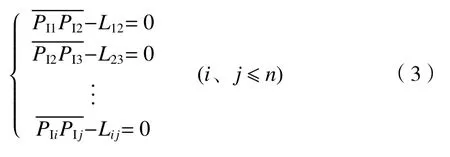
而另一方面，由初等几何知识，可建立几何约束：

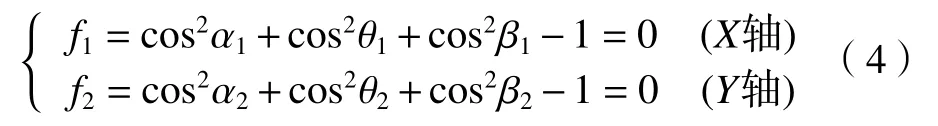
式中：f1与f2分别对应X轴与Y轴的几何约束。将点系平移变换后的球心距和标定参数的几何约束公式（4）带入距离约束公式（2）中，可得转换后的球心距平方与三坐标机检定的球心距平方差值 ∆Iij：

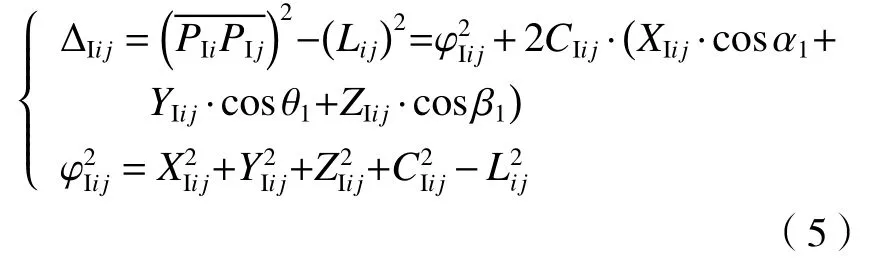
由于误差存在，显然 ∆Iij≠0。为了求解最优的参数，通过非线性优化方法，采用惩罚函数建立具有权因子的目标函数：

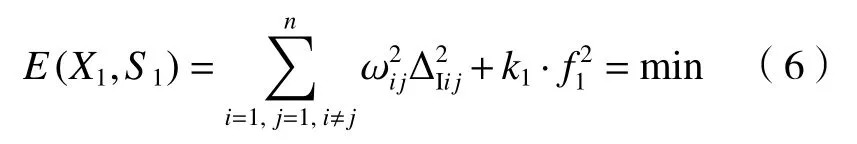
式中：k1是 惩罚因子； ωij是与距离平方正相关的权因子；X1是 表示X轴平移台外参的矩阵；S1是表示参与计算的所有靶球球心坐标的矩阵，分别记为：

由于靶球在靶尺上间隔均匀，扫描仪采集间隔距离大致相等，结合扫描仪的最大视野30 mm×45 mm，因此权因子可设为

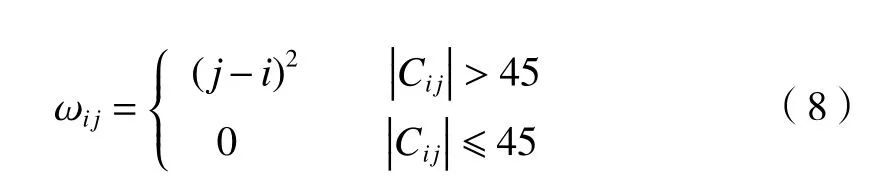
为了求出X1的 最优解，满足E(X1,S1)=min 的条件，需要对E(X1,S1)求导，使得导数为0，即

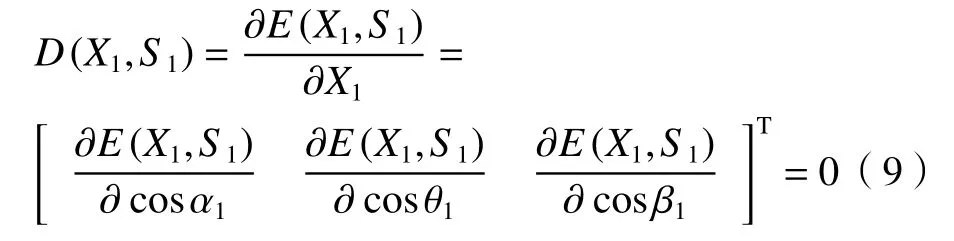
结合公式（8）与公式（4），即可求出目标参数X1=[cosα1cosθ1cosβ1]T。采用相似的方 法，可求出Y轴的标定参数，记为X2=[cosα2cosθ2cosβ2]T。

由公式（5）、公式（6）和公式（9）可知，平移台定位精度和球心坐标误差均会影响标定参数的精度，最终影响拼接精度。而平移台定位精度通常要比扫描仪的测量精度高一个数量级，所以对于本测量系统的标定方法，拟合得到的靶球球心坐标精度对外参精度影响较大。

算法流程图如图3所示。需要注意的是，进行非线性优化计算时，选取恰当的初值，可以提升运算效率、提高结果精度。

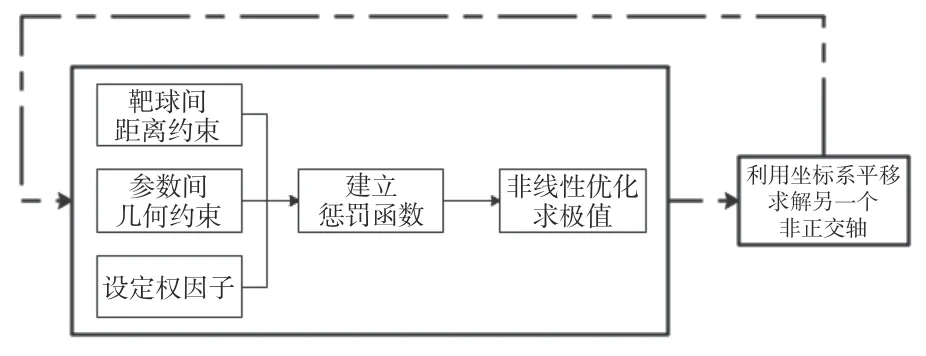
图3 算法流程图Fig.3 Flow chart of algorithm

3 实验

基于之前的理论分析，进行测量系统标定试验、单点坐标转换试验和球心距验证试验，并对真实工件进行测量，以检验测量系统实际的精度和实用性。选用的结构光扫描仪为LMI公司的Gocator 3506，其VDI/VDE精度为12 μm；X轴平移台与Y轴平移台均为PI公司的M-521平移台。该型号平移台行程为200 mm，双向重复定位误差为±0.2 μm。扫描仪与平移台的关键参数如表1、表2所示。选用的标准陶瓷球靶标由8个半径为5 mm级别的哑光标准陶瓷球和长度为200 mm的碳纤维板组成。机械臂与载物台作为辅助机构，用于固定工件位姿。测量系统实物图如图4所示。测量时保证载物台和待测物静止，只操控双轴平移台移动结构光扫描仪。

表1 扫描仪关键参数Table 1 Key parameters of scanner

表2 平移台关键参数Table 2 Key parameters of translation platform

图4 测量系统实物图Fig.4 Physical picture of measurement system

3.1 标定试验

本试验分别控制2个平移台，移动扫描仪拍摄标定靶尺上的靶球，根据第2节提出的标定方法，最终实现测量系统外参的标定。

首先只操控X轴平移台平移结构光扫描仪，逐个拍摄靶尺上的靶球，并提取靶球点云进行拟合，得到每个靶球在扫描仪测量坐标系下的坐标，靶球的扫描效果和拟合如图5所示；根据第2节中的标定方法，带入靶球坐标和平移台坐标值，拟合求解X轴对应的外参；同理求解Y轴平移台的外参。每个轴的外参标定试验分别进行8组，计算得到外参的数值和标准差如表3所示。

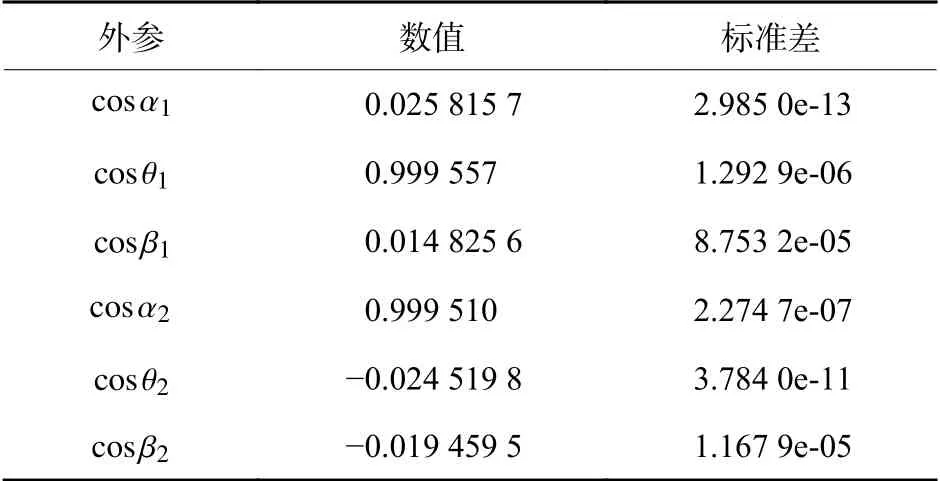
表3 测量系统外参参数Table 3 External parameters of measurement system

图5 靶球点云拟合Fig.5 Point cloud fitting of target sphere

在非线性优化计算前，可以根据扫描仪测量坐标系和平移台运动方向大致的角度设定迭代初值，可设定迭代初值X10=[0 1 0]T， 而X20=[1 0 0]T，这样便可以提高计算效率。

对结果进行分析，发现外参数值的标准差较小，说明该方法得到的结果较为稳定。不难发现，外参标准差大小与平移台运动轴方向有关。具体关联有待进一步研究。

3.2 单点拼接与球心距验证

本试验使用测量系统对尺寸为300 mm的标准球靶尺上的球心坐标进行测量，通过球心距测量系统的精度。

测量系统经标定后同时移动两轴，测量标准靶尺上的验证点球心坐标；然后根据不同拍摄位置在平移台上的坐标值，将扫描仪测量坐标系下的靶球球心坐标统一转换至测量系统坐标系下，分别求解不同验证点间的球心距。分别进行8组实验，数据如表4所示。在300 mm范围内，球心距的均方根误差（root-mean-square error，RMSE）优于45 μm，可证明系统精度较高。3.1节所用标定靶尺和本节实验所用的验证靶标如图6所示。RMSE计算公式为

图6 标定靶尺与验证靶尺Fi g.6 Calibration target scale and verification target scale

表4 部分球心距数据Table 4 Partial data of sphere-center distance mm

RMSE用来衡量观测值同真值之间的偏差，式中x表示真实值。三坐标机的精度远高于结构光扫描仪，故本试验中选用三坐标机检定的靶球球心距作为靶球球心距的实际值。

3.3 工件特征形貌尺寸测量

本试验利用组合式测量系统，扫描支架的栓接安装面，并测量各安装面相对于基准面的高度差，以验证系统的实用性。

分别测量图7（a）工件上的4个栓接安装面。测量范围约为140 mm×160 mm。栓接安装面与基底面大致平行，垂直方向高度差较小。所以可以使扫描仪测量坐标系Z轴尽可能与待测平面垂直，然后根据相对高度阈值进行滤波，得到特征型面的点云。根据结构光扫描仪在十字平移台上的坐标，将不同位置下获得的安装面特征形貌点云进行拼接。将1号面和4号面的点云数据拟合后建立基准面，求解各个特征型面相对于基准面的高度差，如表5所示。

表5 特征型面相对于基准面的高度差Table 5 Height difference between feature surface and datum plane mm

4 结论

为了利用视野较小的高精度三维结构光扫描仪实现大尺寸工件的测量，本文提出了一种基于结构光扫描仪和高精度平移台的组合式测量方法。首先分析了测量系统的组成和测量原理；然后提出了基于加权非线性优化的系统外参求解方法；最后通过实验，对测量系统进行标定，验证测量系统在300 mm范围内的测量精度优于45 μm，并且通过实际测量某型支架的安装面形貌特征，以证明该测量系统的实用性。该测量方法具有精度高、设备组成简单、标定方法简便等特点，能够较好地满足针对多栓接支架安装面的几何形貌测量需求。但本文对外参误差的规律的研究尚有不足，而且应用场景较为单一，这也是后续研究需要解决的问题。