基于多智能体强化学习的自动化电力仓库货位优化

王铁铮，胡亚楠，潘 焜，喻 晓

(国网北京市电力公司 物资分公司，北京 100053)

电力仓库负责供电公司电力项目建设、抢修、维修的物资供应任务。随着自动化大型电力仓库的建设使用和物资供应任务的增多，对于电力仓库的物资管理提出更高的要求。目前自动化大型电力仓库基于货架构造形式分为单元货架形式[1-2]、贯通形式[3]、水平旋转式[4]和垂直旋转货架式。

物资货位优化是影响自动化仓库管理效率的重要因素之一。为了进一步提升自动化仓库管理效率，相关学者在货位优化问题上进行了大量相关研究。印美等[5]以物资出入库距离、货架稳定性为目标建立非支配遗传算法对多目标的货位优化问题进行求解。张思建等[6]基于自动小车存取系统的电力仓库，应用模拟退火算法对多批的物资入库货位分配进行优化。肖锋[7]利用物资历史入库经验数据，使用强化学习算法解决货位分配问题。

基于遗传算法[8]、模拟退火算法[9-10]或粒子群算法[11]进行货位优化问题的求解，已经能够实现单次物资入库时综合考虑多个目标，使得优化后的物资入库货位在多个目标上综合效益全局最优或局部最优。但是该方法在优化时，只能考虑到当前时间点的仓库最优情况，无法考虑到未来物资入库后的仓储情境。基于强化学习[12]的方法构建货位优化算法可以利用仓库的历史物资出入库数据进行模型训练，在货位优化时综合考虑当前时间点的即时奖励和未来奖励，实现电力物资仓库在较长时间范围内的利益最大化。多智能体强化学习算法[13]相对于普通的单智能体强化学习算法[14]，能够更好地处理较为复杂的优化问题，具有较高的稳定性、适应性。本文在MADDPG多智能体强化学习算法[15]基础上，针对货位优化问题，提出改进算法ECS-MADDPG。

1 货位优化目标数学模型

根据电力自动化仓库实际情况和电力物资信息，以提升仓库效率、物资运输能耗和货架稳定性为原则，建立多目标货位优化数学模型。

1.1 仓库物资出入库时间

仓库物资出入库时间越短，仓库物资出入库效率越高，物资运输能耗越低。焦玉玲等[16]以堆垛机Y、Z两个运动方向建立数学模型。研究设定传动带加堆垛机的运输方式，运动速度分别以 vx、vy、vz在X、Y、Z方向上进行匀速运动，忽略传送带和堆垛机启动、制动过程，则仓库物资出入库时间优化的数学描述如下。

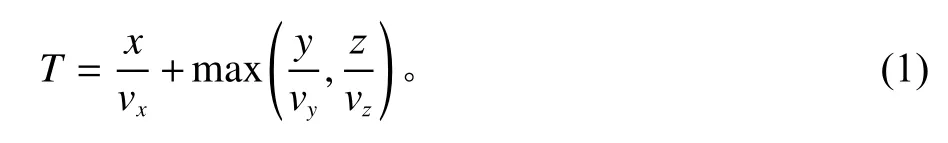
式(1)中，T 为物资单程运输时间，x、y、z分别为在X、Y、Z 3个方向上的位移距离。

1.2 仓库货架垂直质心

仓库货架垂直重心越低，仓库整体物资运输能耗越低，货架稳定性越好。为了使货架整体垂直重心尽可能低，建立数学描述如下。

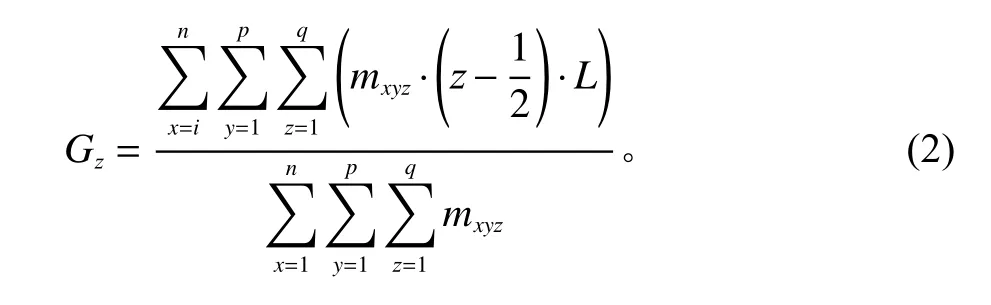
式(2)中，Gz为单个货架的垂直质心值； mxyz为货架上每个货位中物资的质量，空货位质量为0；L为货位的边长；n、p、q分别为在3个方向上位移的步数。

1.3 仓库货架水平质心

仓库货架水平质心越接近中心点，仓库货架稳定性越好。为了使货架整体水平质心尽可能靠近中心点，建立数学描述如下。

式(3)中，Gy为单个货架的水平质心值。

2 ECS-MADDPG货位优化算法设计

2.1 仓库物资出入库时间

强化学习基本的模型是马尔可夫决策过程[17]，一般有4个核心要素：环境状态空间S、动作空间A、环境奖励函数R、环境状态转移函数T。强化学习的算法训练过程就是智能体和环境交互的过程，智能体依据当前环境信息St选择动作At，环境给智能体返回奖励Rt，并更新环境状态到St+1。

在电力仓库货位优化问题中，仓库环境状态信息包括每一个货位的位置信息、所在货架信息、仓库中未摆放货物的货位信息、仓库中摆放货物的货位信息以及对应的货物信息等。Agent感知到的电力仓库环境状态S可表示为

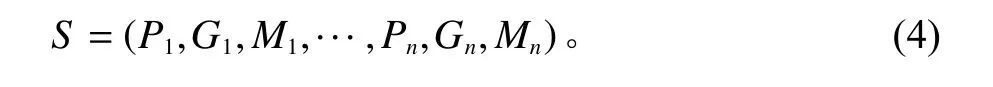
其中，P为货位位置及所在货架，G为物资种类，M为货物质量，n为仓库中的货位数。

在货位优化过程中，物资入库任务可能会有多个物资同时入库。本文研究的多智能体算法为每一类物资设置一个对应的智能体，基于物资种类的变化算法可灵活调节智能体的数量。在一次物资入库任务中多个智能体分别为对应的种类物资规划入库货位，当一次物资入库任务中某一种类物资有多个，一个智能体顺序为多个同类物资规划入库货位。智能体的动作执行空间为选择一个仓库中的空置货位。由于多个智能体并行规划物资的货位时可能出现多个物资分配到同一货位的异常状况，设定同一批入库物资由多个智能体顺序执行物资货位规划。

在电力仓库货位优化问题中，物资入库任务和物资出库任务时常出现交替情况，货位优化算法仅在物资入库任务阶段执行。因此当两次物资入库任务之间存在物资出库任务时，第1次物资入库动作执行后的仓库环境和第2次物资入库动作执行前的仓库环境可能存在不一致，因此传统的强化学习中智能体与环境的交互过程无法满足需求。研究提出货位优化问题中强化学习智能体与环境的交互过程，如图1所示。

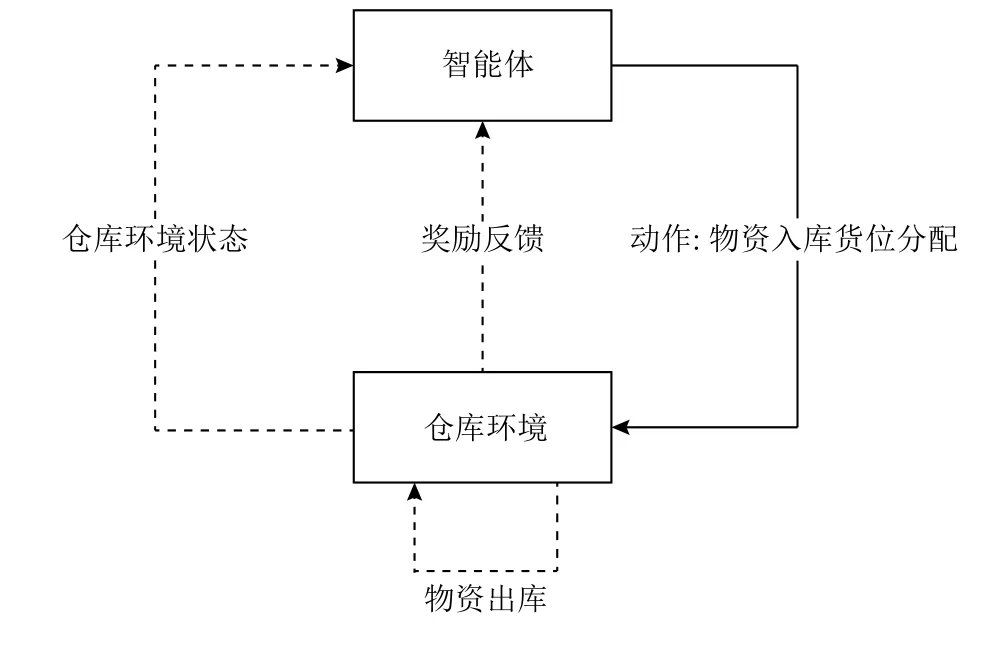
图1 强化学习的智能体与环境的交互过程Figure 1 The interaction between the agent and the environment in of reinforcement learning

图1 中智能体根据物资入库时的仓库环境执行物资货位分配动作后，仓库环境不会立刻给予智能体新的仓库环境状体和奖励反馈，而是当有新的物资入库时，智能体获得前一次执行动作后的奖励以及新的仓库环境状态。

2.2 奖励函数设计

奖励函数负责计算智能体为入库物资分配货位的效果收益。针对电力仓库货位优化的需求，设定仓库所有物资的出入库运输时间、所有货架垂直重心和水平重心的平均值为优化目标。多个智能体为完全合作的关系，常用的奖励函数设计方式为多个智能体使用相同的奖励函数，这样多个智能体得到的回报也是相同的，多个智能体的联合动作目标为获得整体最大化回报。实验过程中发现，多个智能体采用相同奖励函数的方式会导致部分智能体产生惰性，进而影响多个智能体的整体回报。本文设计的奖励函数为混合奖励机制，智能体执行动作后，环境将同时给予智能体单独的奖励以及所有智能体联合动作的整体奖励。该奖励机制使得多个智能体之间既有合作关系也有竞争关系。通过引入多个智能体之间的适度竞争提升了多个智能体的联合动作的整体回报。

电力仓库中所有物资的运输时间受到仓库中物资所在货位位置和物资的存储时间影响。对于存储时间短的物资，算法应偏向于为物资分配距离仓库出入口较近的货位，反之应偏向于为物资分配距离仓库出入口较远的货位。

针对货位优化问题的特性，设定智能体执行货位分配动作后的奖励由2部分构成。第1部分为智能体执行动作引起环境变化得到的单独奖励，如式(5)所示。

式(5)中，T表示单个物资运输到指定货位的时长；Gz和Gy分别表示单个物资放置到货位后，该货位所在的货架的垂直质心数值和水平质心数值。W为T、Gz和Gy对于智能体奖励值影响的权重；Fnor为maxmin归一化函数，函数细节如式(6)所示，max和min值分别为变量x的最大可取数值和最小可取数值。通过归一化函数可将多个不同量纲的指标数据转换为同一量纲指标。式(5)中，d表示该物资当前入库时间与该物资下一批次入库时间之间相差的天数，相差时间越高说明物资入库频率可能越低，物资出入库运输时长对仓库整体的优化目标较小，因此通过动态调整指标数值映射范围调低该指标对整体优化目标的影响。由于T、Gz和Gy数值越低表示算法优化效果越好，因此奖励值取T、Gz和Gy加权求和的倒数。

第2部分为同一批次执行物资分配任务的多个智能体执行的联合动作引起环境变化得到的整体奖励，如式(8)所示。

式(8)中，表示同一批次所有物资运输到指定货位的时长总和；分别表示该批物资入库货位对应的所有货架的垂直质心数值总和以及水平质心数值总和。

智能体执行动作得到的单独奖励和多个智能体联合动作得到整体奖励加权求和值为单个智能体的最终奖励，奖励函数如式(9)所示。

2.3 ECS-MADDPG算法

DDPG算法[18]是一种使用Actor-Critic算法框架和深度确定性策略梯度方式的强化学习算法。该算法分为Actor和Critic两个部分。

Actor网络部分由Actor主网络和Actor目标网络组成。Actor主网络负责根据当前环境状态S选择动作A，得到环境反馈值R和新的状态S′；同时更新网络参数θu，并将交互数据以多元组 〈 S,A,R,S′〉的形式存入经验池E中，表达式如式(10)。Actor目标网络负责从经验池中随机采样状态S′并 产生动作A′，Actor目标网络参数 θu′通 过复制参数 θu更新，表达式如式(11)，式中u为目标值参数。

Critic网络部分由Critic主网络和Critic目标网络组成。Critic主网络负责计算预估值q并更新网络参数θq，表达式如式(12)。Critic目标网络负责计算目标值q，网络参数 θq′通过定期复制θq更新，表达式如式(13)。Critic部分主要作用是优化网络参数。

MAGGPG算法将DDPG算法思想拓展应用到多智能体强化学习领域，使用多智能体集中训练，独立分布式执行动作的架构，每一个智能体拥有自己独立的Actor和Critic网络。在训练环节，智能体的Actor网络仅使用智能体自身可获得的环境信息。Critic网络利用智能体自身获得的环境信息以及其他智能体的动作信息等进行训练，并指导Actor网络的参数更新。在预测环节，每一个智能体可独立执行动作。

ECS-MADDPG算法在MAGGPG算法的基础上针对货位优化问题，设计执行相似任务的智能体共享经验池和Critic网络的方式改进模型训练时长和部分智能体可能无法收敛的问题。研究设定每一类物资设置一个对应的智能体，不同智能体执行任务的差异在于其对应的不同物资的装箱质量和出入库频率不同。通过物资的质量和出入库频率对部分出入库频率较低的物资进行K-Means聚类，将物资与智能体分为几个大的类别。大类别内部智能体共享经验池和Critic网络，当智能体Actor主网络在状态S产生动作A后，会将数据交互元组 〈 S,A,R,S′〉存入共享经验池E，多个智能体从共享经验池中随机采样数据，并使用和更新同一个共享Critic网络。货位优化问题中算法训练过程不同智能体执行动作的次数不同，通过共享经验池的方式可使得交互数据比较少的智能体拥有更丰富的经验交互数据，从而减少模型整体训练时长和交互数据比较少的智能体的收敛时长。ECS-MADDPG算法结构如图2所示。

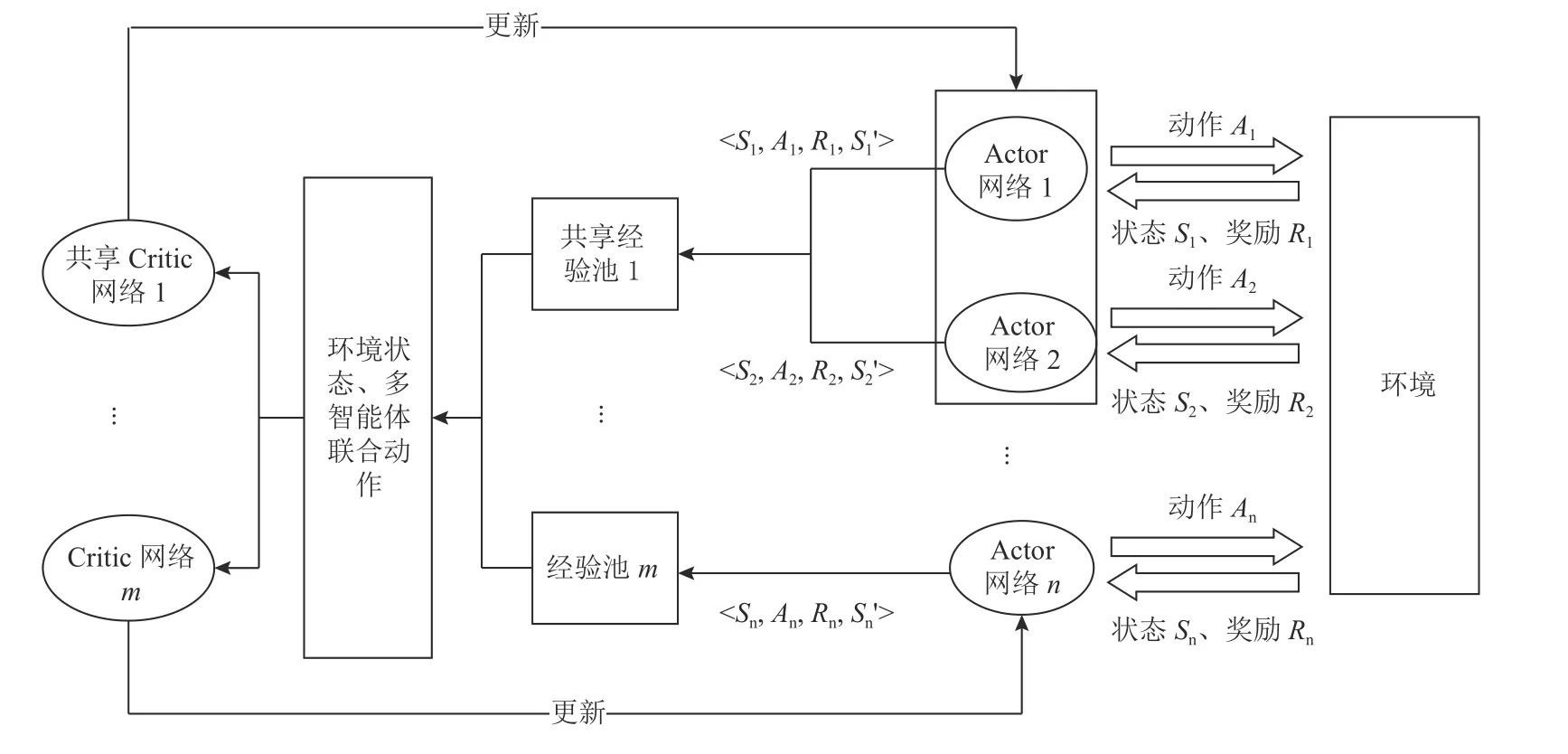
图2 ECS-MADDPG算法结构Figure 2 The structure of the ECS-MADDPG algorithm

ECS-MADDPG算法流程如下所示。

1) 初始化n个智能体的Actor和Critic网络参数。

2) for k=1 to 最大回合数。

3) 初始化仓库物资状。

4) for t=1 to 最大物资入库次数。

5) 多个智能体通过Actor主网络进行动作选择ai=µ(Si)， 执行动作获得环境奖励r和新的状态 S′，将多元组 〈S,A,R,S′〉智能体-环境交互数据分别存入对应的经验池。

6) for agent=1 to 最多n个智能体。

7) 随机在多个经验池中采样W组 〈 S,A,R,S′〉交互数据，组成联合交互数据。

8) Critic网络目标q值计算，其中γ为常数值参数

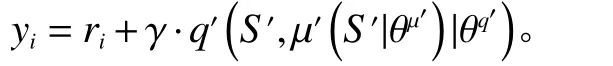
9) 损失函数计算并更新Critic主网络参数，损失函数如下，其中表示第i个智能体的状态-动作函数。

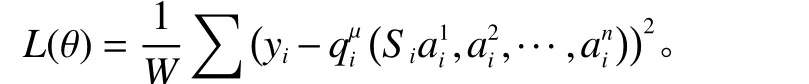
10) 通过策略梯度更新Actor主网络参数，计算公式如下，其中表示第n个智能体在时间步下的环境观察信息。

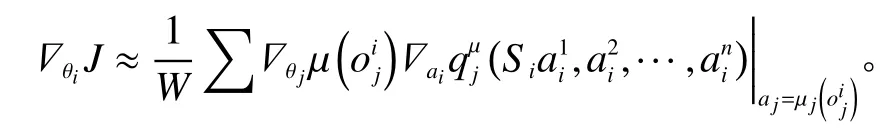
11) 更新Actor和Critic目标网络，其中 τ为常数参数值，表示权重。

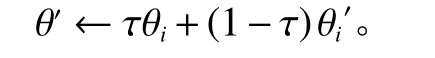
3 实验结果及分析

实验的电力自动化仓库共有3个相同规模的仓库，每个仓库有18排货架，每排有16列8层高，每一个仓库有2 304个货位，所有货位尺寸相同。电力仓库水平方向使用传送带进行物资传送，垂直方向使用堆垛机进行物资运输。仓库货位长宽高尺寸为2 500 mm×1 000 mm×4 500 mm，单个货位最大承受重力为1 t。自动化仓库如图3所示。

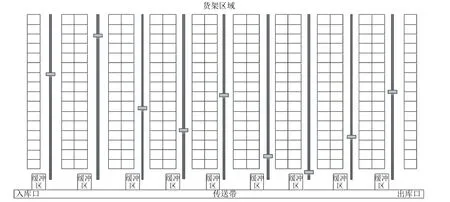
图3 电力自动化仓库俯视图Figure 3 Top view of power automation warehouse

为了验证本文提出的ECS-MADDPG强化学习算法的效果，实验设计使用MADDPG算法、DDPG算法、DQN算法作为对照组。实验数据使用9个月的某电力物资仓库物资出入库数据。初始时，3个仓库已存有电力物资的货位分别为1 534个、974个和367个。通过均匀分布和正态分布方式对3个仓库初始物资摆放位置进行随机分配，每种分布生成10组初始随机仓库物资分布。实验数据中的物资统一装入相同尺寸规格的箱子中，不同物资装入箱中的数量和装箱后总质量不相同，箱子尺寸小于货位尺寸。部分物资装箱数量和质量样例如表1所示。

表1 物资装箱数据样例Table 1 Sample packaging data

实验过程中每一轮3个电力仓库分别有462批次、951批次和1 267批次物资入库，每一批次物资入库数量不等。图4表示1号仓库实验组和对照组算法在1 000回合的迭代过程中获得的平均回报。

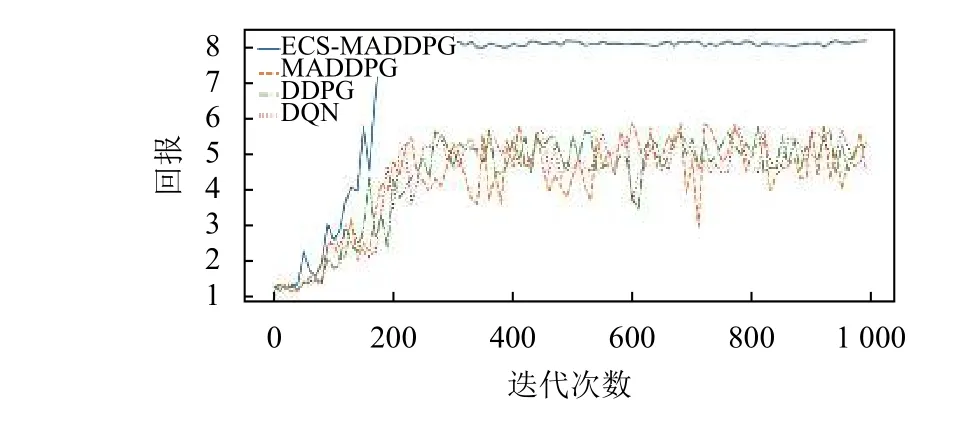
图4 1号仓库各算法迭代次数对应的平均回报Figure 4 Average reward corresponding to the number of iterations of each algorithm in warehouse 1

图5表示2号仓库实验组和对照组算法在1 000回合的迭代过程中获得的平均回报。

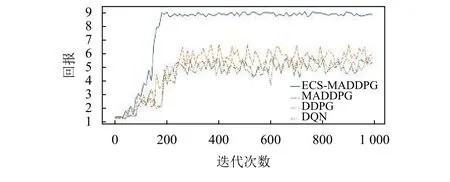
图5 2号仓库各算法迭代次数对应的平均回报Figure 5 Average reward corresponding to the number of iterations of each algorithm in warehouse 2

图6表示3号仓库实验组和对照组算法在1 000回合的迭代过程中获得的平均回报。

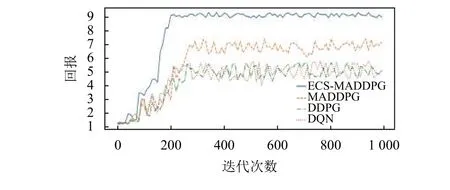
图6 3号仓库各算法迭代次数对应的平均回报Figure 6 Average reward corresponding to the number of iterations of each algorithm in warehouse 1

通过图4～6可以发现，ECS-MADDPG算法在3组仓库环境中通过200次迭代均可以收敛，MADDPG算法在3组仓库环境中通过250次迭代均可以收敛，DDPG算法和DQN算法在3组仓库环境中通过230次迭代可以收敛。MADDPG算法随着实验每一回合入库物资批次增多有较为明显的稳定性和最高平均回报值的提升，说明入库物资批次较少时，非共享结构的MADDPG中可能存在部分智能体网络学习不充分的现象。ECS-MADDPG算法在3组仓库环境中模型效果的稳定性和最高平均回报值均优于其他3组对照组实验。

4 结论

本文提出了一种多智能体强化学习的电力仓库货位优化算法。该算法在货位优化时同时考虑当前时间点的即时奖励和未来奖励，实现电力物资仓库在较长时间范围内的所有物资的出入库时间、货架的重心加权指标在较长时间范围内为较优的结果。实验表明，相对于普通单智能体和多智能体强化学习算法，ECS-MADDPG算法效果具有较高的稳定性和回报值。