基于PIWOA的绿色闭环供应链网络多目标模糊优化设计

董 海，吴 瑶

(沈阳大学 1.应用技术学院；2.机械工程学院，辽宁 沈阳 110044)

随着全球变暖加剧和工业全球化，企业对于环境、社会效益的重视日渐提高。近年来，在Listes等[1]最早研究了闭环供应链网络设计并提出了随机规划模型之后，越来越多的学者在进行闭环供应链(closed loop supply chains，CLSC)网络设计时开始考虑环境和社会效益等因素。Pati等[2]利用混合整数目标规划模型设计一个多产品纸张回收网络，用以降低总成本，并通过提高废纸回收率实现环境效益。Dehghanian等[3]利用生命周期分析(life cycle analysis，LCA)和层次分析法(analytic hierarchy process，AHP)建立一个多目标数学规划模型，使经济效益和社会效益达到最大化。Devika等[4]也通过同时考虑CLSC中经济、环境和社会因素，建立混合整数规划模型。Chen等[5]从可持续性的角度考虑太阳能行业的供应链成本和环境问题，并研究集成CLSC网络的设计问题。Sahebjamnia等[6]在保护环境和最大化社会效益的前提下，研究轮胎行业可持续CLSC网络设计的混合整数线性规划模型，用以优化总成本。吕宝龙等[7]在考虑利润最大化的同时，兼顾碳税情况和产品绿色度，研究闭环供应链网络Nash均衡模型。

现实生产中的CLSC网络的设计，有很多的不确定性，而这些因素往往会造成企业风险较大，成本较高等问题。学者在CLSC网络的设计上，大多采用随机规划、模糊规划和鲁棒控制等方法降低不确定性的影响。Ozceylan等[8]提出不确定性条件下CLSC网络的多产品、多周期的混合整数模糊数学模型，并借助线性隶属度函数实现参数和目标的确定性转化。Ozkir等[9]开发一种强调客户满意度和净利润的多目标CLSC网络模型，并采用模糊集理论进行求解。Ozceylan等[10]建立战术和战略决策场景下的CLSC网络规划模型，并利用模糊交互方法解决CLSC网络设计问题。Tsao等[11]提出一个基于CLSC网络的可持续多目标规划模型，引入一个交互式的两阶段模糊概率法来处理各种不确定性。Fakhrzad等[12]提出一个基于模糊数的多目标混合线性整数规划模型，达到成本最小，碳排放最小且供应商可靠性最强的目标。但以上文献均采用悲观值或乐观值处理模糊问题，结果具有极端性。

CLSC网络设计是一个NP-hard问题，解决此类问题多采用智能算法。Pishvaee等[13]通过基于特殊局部搜索的模拟退火算法解决了多级RL网络的规划模型。Wang等[14]将环境问题整合到一个整数CLSC模型中，并提出一种基于生成树结构的遗传算法求解所提出的模型。Fakhrzad等[15]在解决多目标CLSC网络设计的NP-hard问题时，采用非支配排序遗传算法进行求解。但传统的智能算法步骤繁琐且用时较高，2016年Mirjalili等[16]开发的鲸鱼优化算法(whale optimization algorithm, WOA)具有原理简单，人工参数少和收敛速度优等特点。

综上，本文构建基于Me测度的CLSC网络的模糊规划模型，并提出一种基于帕累托(Pareto)最优的改进鲸鱼算法(Pareto improved whale optimization algorithm，PIWOA)求解绿色CLSC网络优化设计问题，最后通过实例验证所提模型及算法的优越性。

1 模型建立

1.1 问题描述

本文研究一个多层级、多周期的CLSC网络，如图1所示。其中包含7个节点：原材料供应商I、制造中心M、配送中心D、客户集合C、分离中心S、处理中心O和回收中心R。正向流动包含原料供货给制造中心生产，再由配送中心分发给客户。逆向物流包括客户中心退回的产品由分离中心挑拣，可回收再利用的货物发到回收中心转运给制造中心进行再制造，而无法再利用的产品发给处理中心进行统一销毁或填埋等处理。本文主要解决供应链运营成本最低，碳排放最小和社会效益最大的闭环供应链网络多目标优化问题。

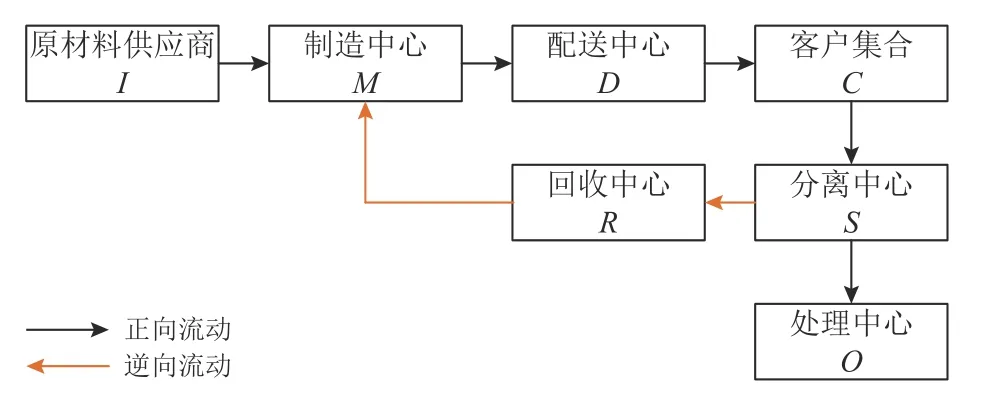
图1 CLSC网络结构图Figure 1 CLSC network structure diagram

1.2 模型假设及符号定义

本文假设如下：1) 产品回收利用能够节约成本；2) 每个节点设施均有容量限制；3) 制造与再制造的生产成本一致，再制造只省掉一部分原材料费用；4) 客户集合和原材料供应商的位置已知且固定，对于各类产品需求也已知；5) 各节点间运输只采用一种运输方式。基于建模需要，定义符号如表1～4。

表1 模型中集合定义Table 1 Collection definitions in the model

本文建立如下模型Z1、Z2、Z3。

目标函数1(Z1)表示最小化网络成本，分别包含原材料成本、各个节点的建设费用、配送运输费用、正逆向物流的节点处理费用以及回收节省的原料费用。目标函数2(Z2)表示最小化环境污染，分别包含建设时CO2排放量和运输时CO2排放量。目标函数3(Z3)表示最大化社会效益。约束条件主要包含各节点流量约束和各节点能力约束，具体模型如式(1)～(3)，约束条件如式(4)～(15)。

表2 模型中参数定义Table 2 Parameters in the model

表3 0-1变量Table 3 Variables 0-1

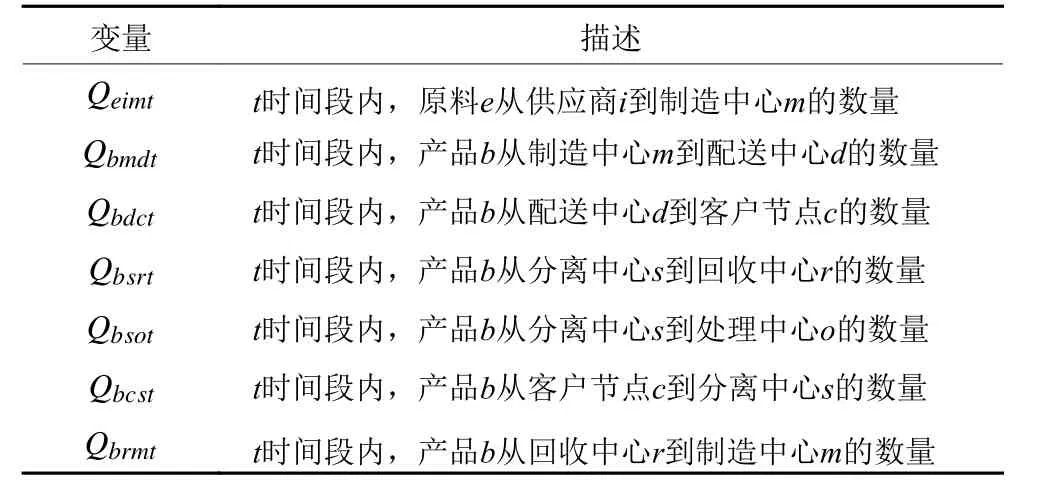
表4 决策变量Table 4 Decision variables

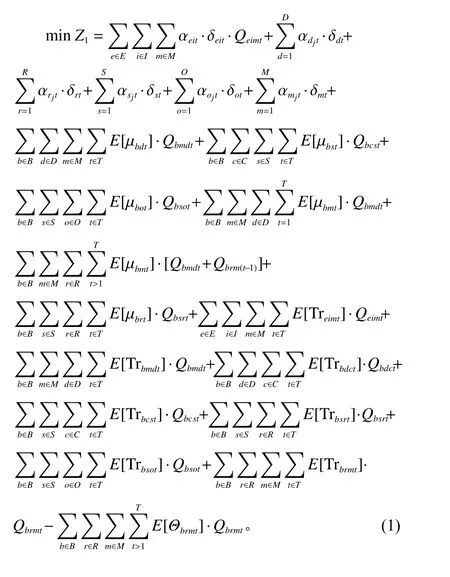
式(4)～(9)和 式(13)中 ξi、 ξd、 ξr、 ξo、 ξs、 ξm、ξcϵ[0,1]，表示节点I、D、R、O、S、M、C的能力约束的置信水平。式(10)～(12)表示配送中心、再制造中心、分离中心的流量守恒，式(14)～(15)表示客户中心的可用产品数量约束和决策变量取值约束。

2 模型处理

为减弱模型中的不确定性，本文采用模糊规划方法对已建模型和约束进行模糊处理。以往文献的模糊测度均采用极端值表示。例如，Pos表示可能性测度，极喜；Nec表示必要性测度，极悲，此类方法数据测定不够准确。而本文的模糊测度采用Xu等[17]提出的Me测度法，此类方法能够实现在2个极端值间灵活变化，减小结果的误差性。具体定义如下[18]，其中 λ是事物发生的概率参数，A表示事件。

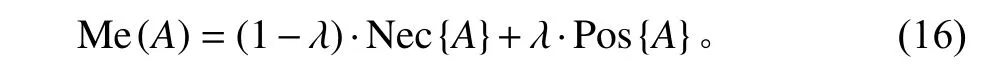
其中， λ∈(0,1)。下式中，引入Me测度水平值K， K ∈[0.5,1]。

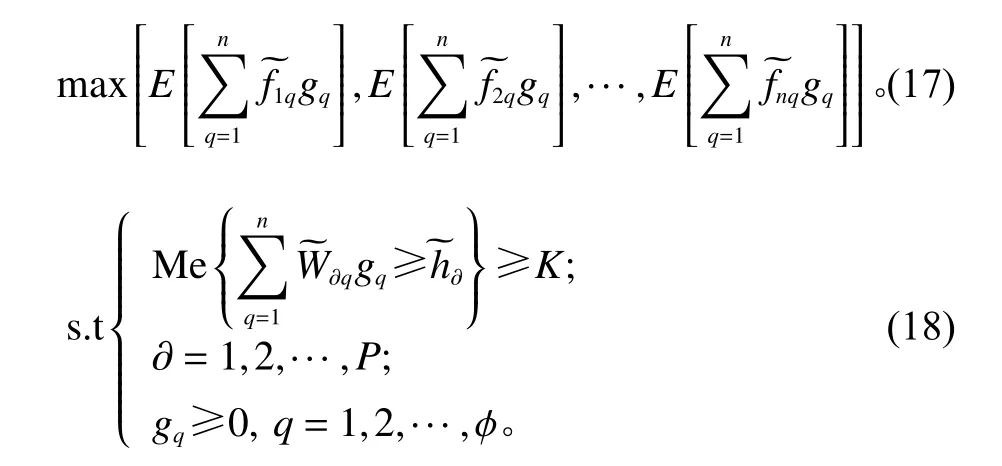
对应上下界估计模型如下。

据此目标函数1的清晰等价模型Lower和Upper如Z4所示。

式(31)～(34)同式(10)、(11)、(12)、(14)。

Lower

s.t.

式(35)～(38)同式(31)～(34)。

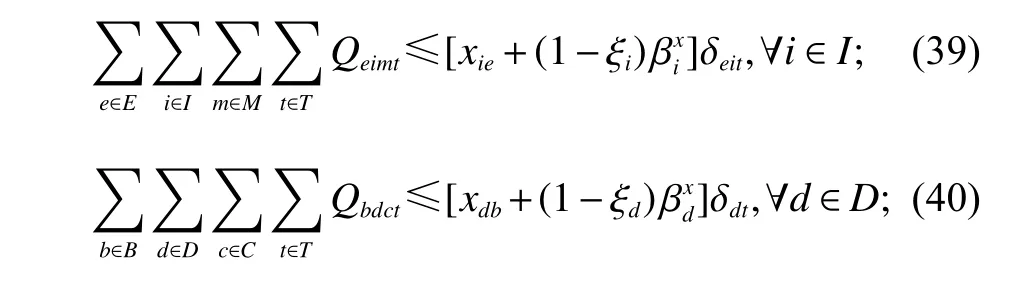
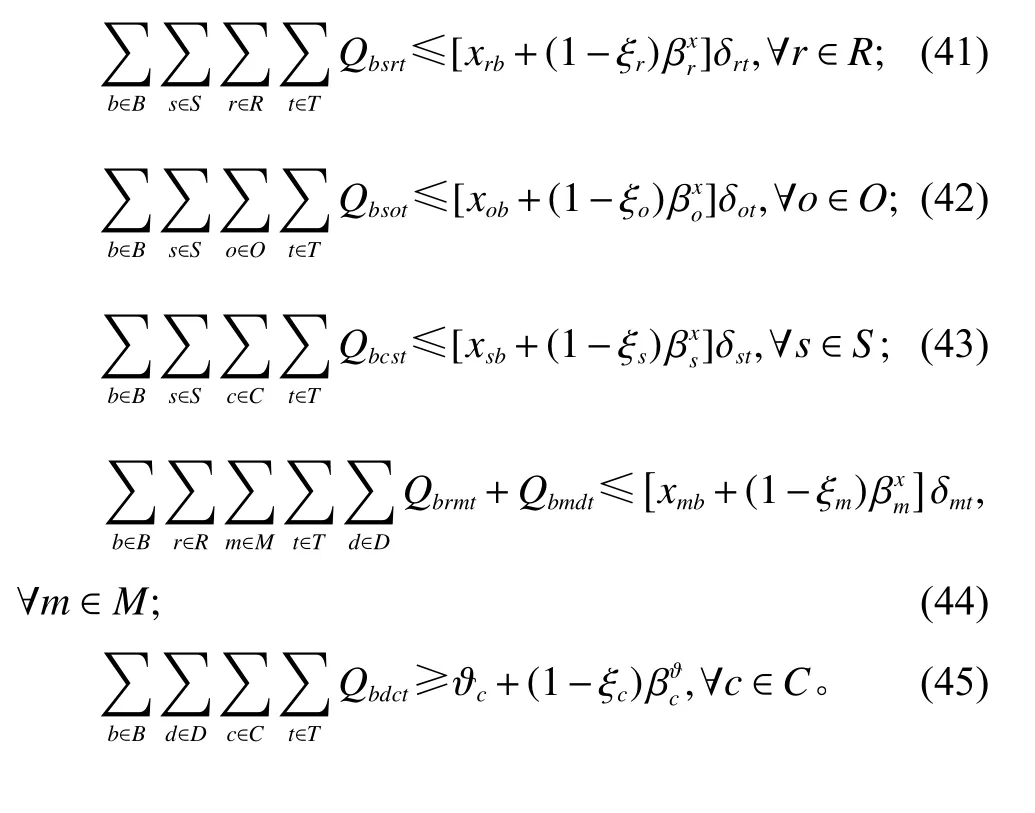
3 求解方法

本文中所采用的解决方法是WOA算法。近几年来，WOA算法因其操作模式简单，人工参数量少，已应用于许多大规模求解问题。但在传统的WOA算法中，其结果容易陷入局部最优的状态，使问题难以得到最优值。基于此类问题，本文引入变异因子，并结合实数编码和Pareto优化方法，对WOA算法进行改进，得到改进后的鲸鱼算法(PIWOA)，该算法力求在解决多目标问题的基础上，提高全局搜索能力的同时又避开了局部最优值。

3.1 原始的鲸鱼算法

WOA的基本思想是通过模拟鲸鱼独特的捕食行为和社会行为来进行优化。通过3个数学模型模拟了包围猎物、气泡网攻击和寻找猎物的过程。

3.1.1 包围猎物

该阶段选择一个搜索代理，将其定义为前一代中的最佳解决方案。其他搜索代理试图避开最优代理来实现全局搜索，具体描述如下。

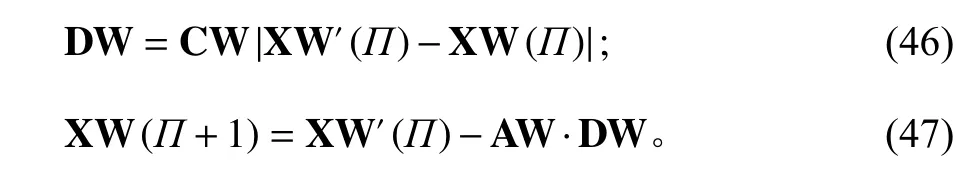
式中， Π 代表当前迭代次数； D W是包围步长；AW和 CW是系数向量； XW(Π)是当前鲸鱼位置向量； XW′(Π)是 当前最优鲸鱼位置向量；XW(Π+1)是每一次迭代中需要更新的最佳位置向量。系数向量A W和C W的计算如下。

其中，ς称为收敛因子，其随迭代次数增加从2线性递减到0；rand为[0,1]之间的随机数。ς的求解公式如下。

Π为当前迭代次数，Πmax是最大迭代次数。

3.1.2 泡沫网攻击

鲸鱼在捕食的时候通常采用螺旋运动的方式先包围猎物，再进行捕猎。

在这一阶段讨论了2种方法：收缩环和螺旋更新位置。收缩环的机制与全局搜索相似，并取值AW[−1,1]。另一种方法是螺旋更新位置,根据当前位置和最优代理构造对数螺旋曲线，使得搜索代理逐步逼近最佳位置。具体描述如下。

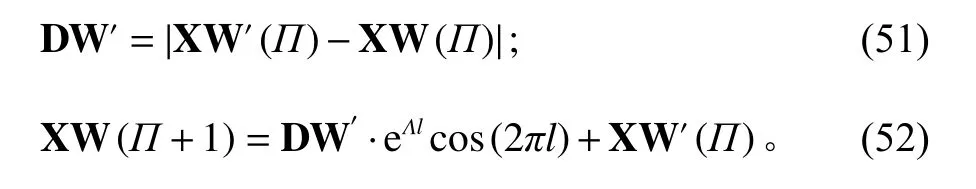
式中， D W′指当前鲸鱼与最佳位置(也就是与猎物位置)的距离；Λ为对数螺旋形状的常数量；l是介于 [ −1,1]之间的随机数。

3.1.3 搜索猎物

搜索猎物采取鱼群随机性位置更新的方法，数学模型如下。

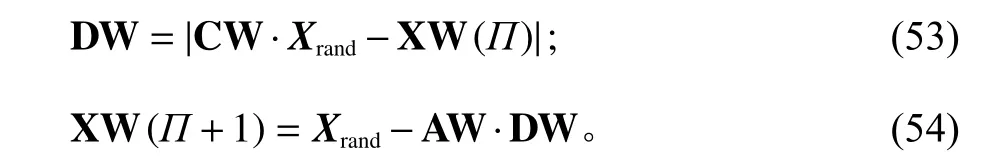
式中， Xrand是 随机所得的位置向量，如果 A W超出 [−1,1]的范围，就通过随机寻找鲸鱼个体，并根据个体的方位，排查其他鲸鱼位置，面向全局搜索找到合适的猎物。

3.2 变异操作

为了更准确地找到全局最优位置，避免陷入局部最优并保证在搜索后期具有较快的收敛速度，本文对原有式中收敛因子 ς进行深层考虑，该因子可以在搜索前期使最小值与迭代次数成正比，同时又能将 ς在增大到较大值时与迭代次数成反比。考虑以上内容，本文将随进化迭代次数而非线性变化的收敛因子更新，公式如下。

其中，ςstart与ςfinal为 ς 的 初值与终值，Ω ＞0，称为非线性调节系数[19]。

3.3 编码与变量处理

模型中决策变量只能取0-1，利用rand函数和round函数随机取值0/1。本文采用平均随机数生成函数配合约束系数，得到决策变量。在计算中，各个变量均采用实数编码方法进行编码。将个体适应度子集F编码为群体中的解 Xτ(τ =1,···,θ)，假定子集包含 θ个个体适应度的值，即F={F(ρ1) ，F(ρ2),···,F(ρθ) }，若F(ρθ+1) ＞F(ρθ) ，则F(ρθ+1)被选择。

3.4 多目标优化处理

解决多目标问题时，可将模型转化成如下。

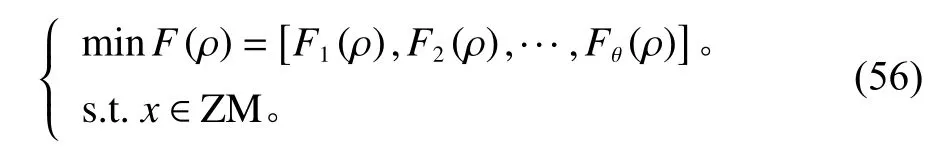
式中，ρ的集合ZM为问题的决策空间；Fτ(ρ),(τ=1,2,3,···,θ)为 目标函数；θ维函数称为问题的目标空间。多目标优化问题无法达到每项最优，只能得到相对最优解集，而最优解的集合称为非支配集。

经处理过后的PIWOA算法如图2所示。图中P是用于确定选择搜索环绕还是螺旋更新位置的因子。假设收缩包围机制和螺旋位置更新概率相同，均为0.5。

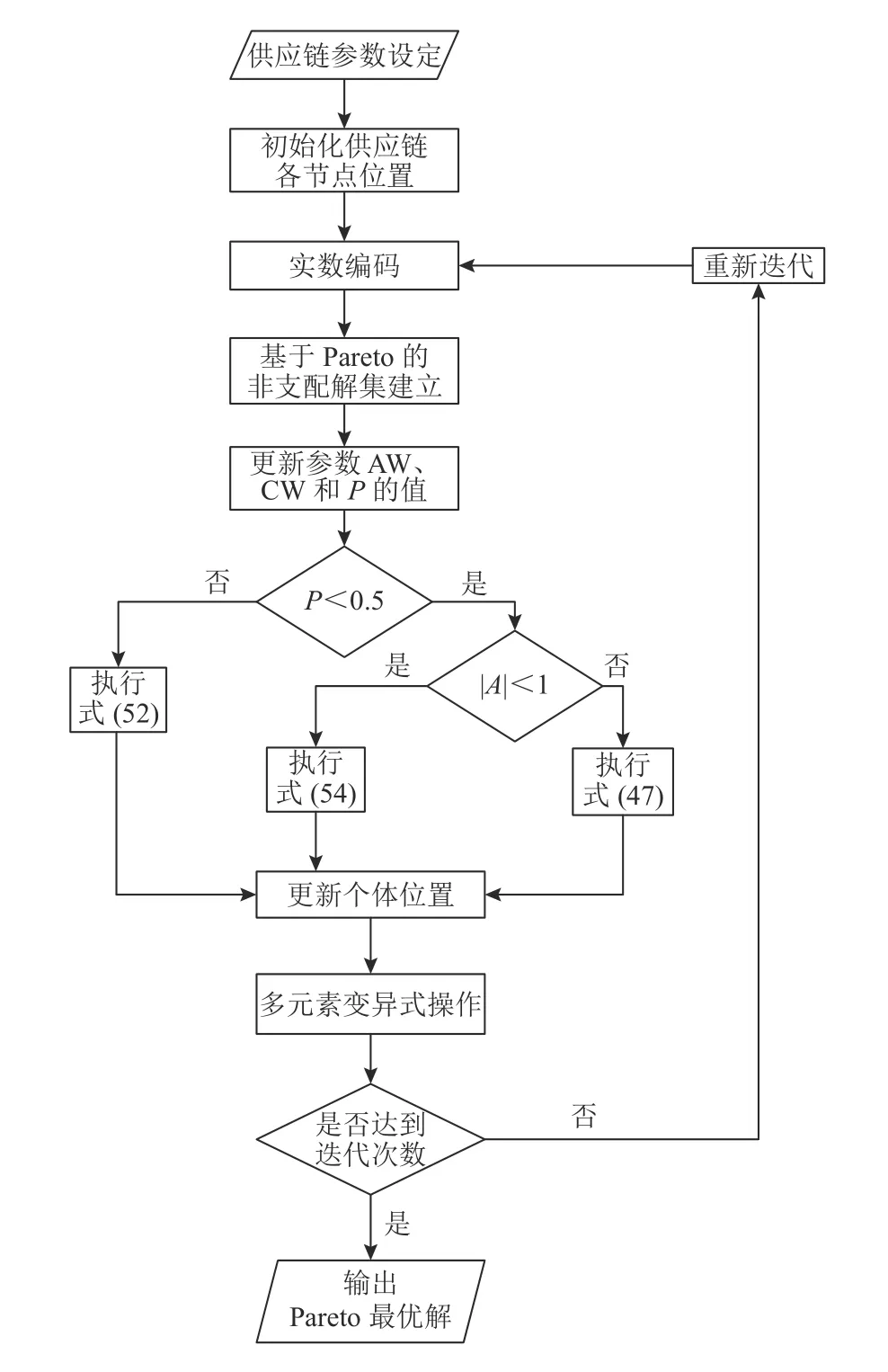
图2 PIWOA算法流程Figure 2 PIWOA algorithm flow

4 算例分析

本文以某玻璃制造厂商为例，此供应链由原料供应商、制造中心、配送中心、客户、分离中心、处理中心和回收中心7个节点组成。为评价本文采用的PIWOA算法的性能，本文将PIWOA与WOA和遗传算法(GA)在Matlab软件上运行并进行比较。Matlab的运行计算机环境为：处理器为Intel(R)Core(TM)i7-8550u CPU＠ 3.9 GHz，内存8 GB，操作系统为Window10的手提电脑。

本文针对目标函数共生成10个测试问题如表5，参数范围如表6，并运用PIWOA算法、WOA算法和遗传算法对每个测试问题运行20次，得到表7。在表7中权重ζ1、 ζ2、 ζ3的取值是根据不同测试问题中相关成本所占的比重而确定的。将种群规模都为200的PIWOA算法、WOA算法和GA算法设置相同数据进行400次迭代，目标函数1的Lower与Upper函数值与迭代次数曲线如图3、4所示，函数平均值与计算时间曲线如图5所示。

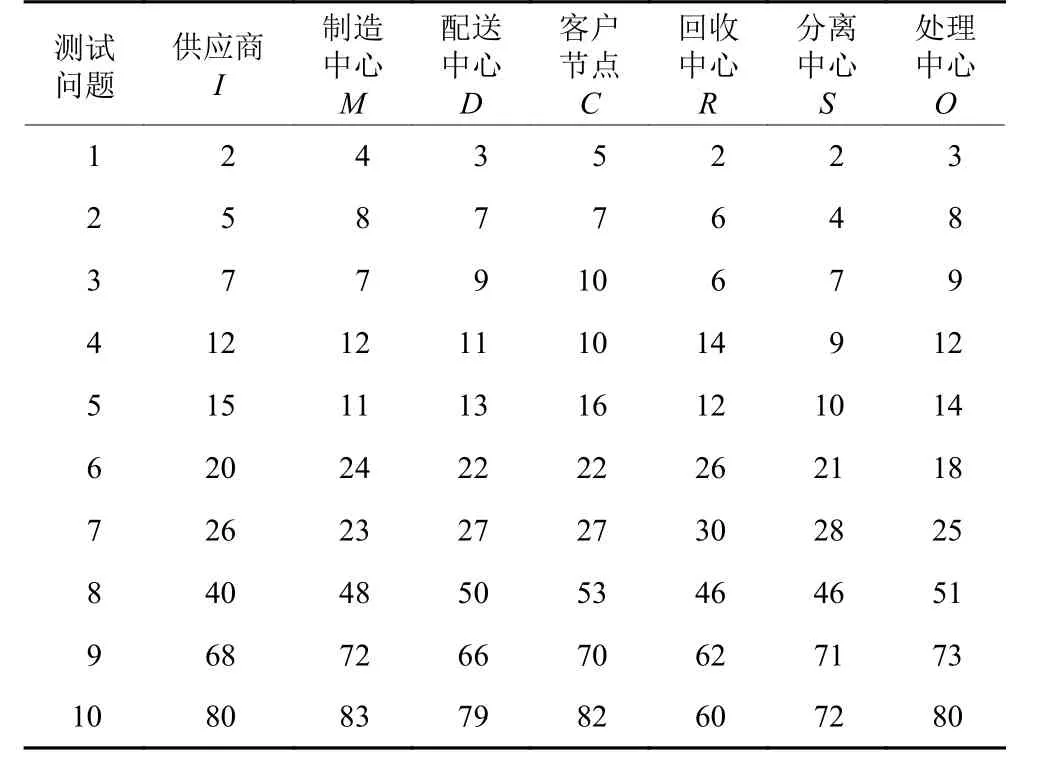
表5 测试问题Table 5 Test questions

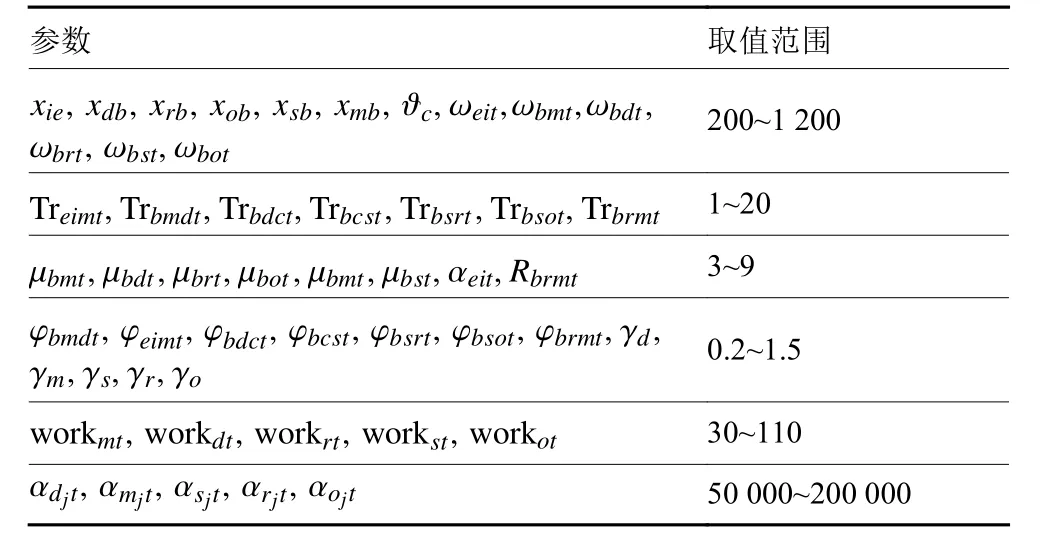
表6 参数取值范围Table 6 Parameters scope

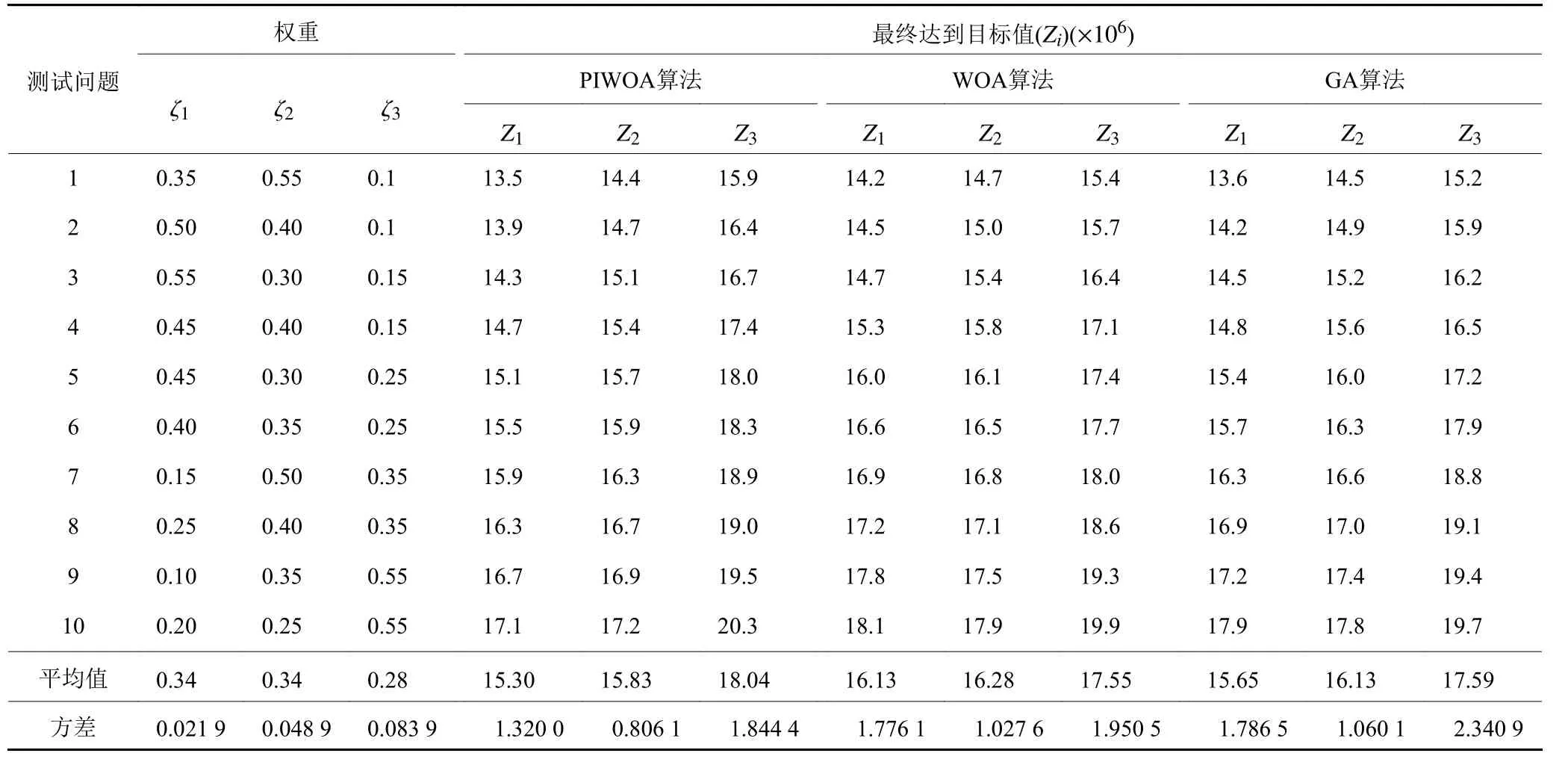
表7 算法计算结果Table 7 Results of algorithm calculation

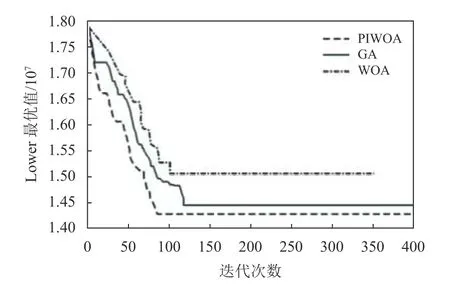
图3 Z1的Lower最优值与迭代次数图Figure 3 The lower optimal value of Z1 and the graph of iteration times

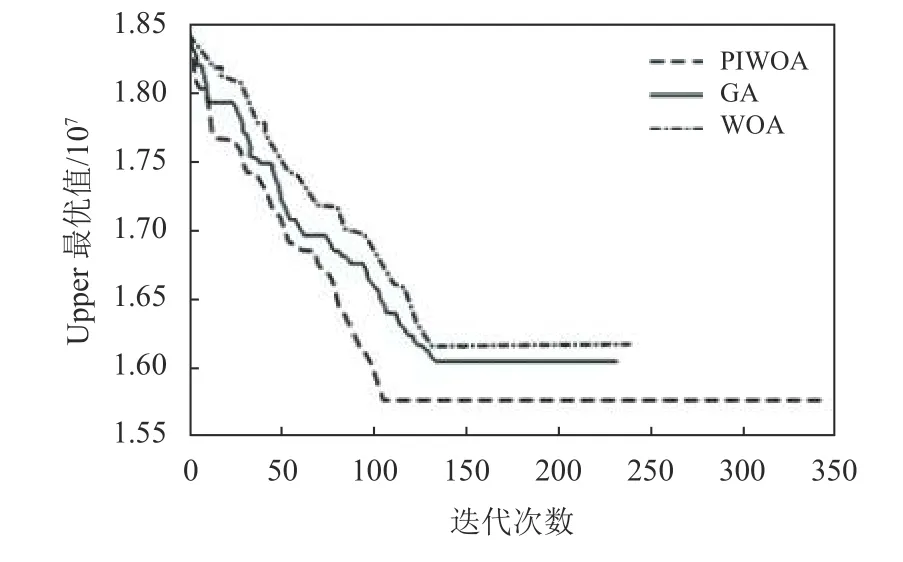
图4 Z1的Upper最优值与迭代次数图Figure 4 The upper optimal value of Z1 and the graph of iteration times

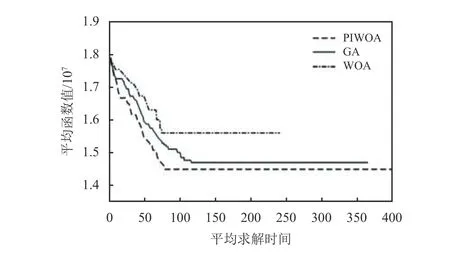
图5 Z1的平均函数值与求解时间图Figure 5 Average function value and solution time diagram of Z1

根据表7中3组数据对比可得，使用PIWOA算法时，总成本Z1整体数值最小，CO2排放量Z2整体数值最小，社会效益Z3整体数值最大，方差最小，稳定性最强。而WOA算法相比于GA算法，总成本Z1整体数值偏大，CO2排放量Z2整体数值偏多，社会效益Z3整体数值趋同，但方差更小，所以WOA算法稳定性更强。根据图3、4可得，无论Lower函数还是Upper函数，采用PIWOA算法对比WOA算法和GA算法总是能更快地跳出局部最优，精确寻找到最优解且成本函数值总是相对更低。而WOA算法与GA算法相比，成本虽略高些，但WOA算法可以更快搜索到最优解。同时，通过图5可知PIWOA的算法时间最短，其次是GA和WOA。

5 结论

针对绿色闭环供应链网络设计的模糊优化问题，本文得出以下结论。

1) 建立以成本最小、CO2排放最小和社会效益最大的目标函数，并采用Me测度和三角模糊数对模型和约束进行模糊处理，通过实例验证，采用模糊处理后的闭环供应链网络优化模型可以减弱模糊影响并取得较好的结果。

2) 采用PIWOA算法解决NP-hard问题，并将该方法与WOA算法和GA算法进行对比。结果表明，PIWOA算法计算时间较短，能够较快跳出局部最优且稳定性强，在处理闭环供应链网络设计问题时，具有较好的优越性。

3) 实际生产中，供应链成员成分更为复杂，很多货物要考虑时间约束，下一步的研究工作主要考虑货物种类多样性对于闭环供应链网络设计时的影响，以保证闭环供应链网络设计更加贴近现实生产。