边界条件和激励位置对高速列车车窗声振特性影响研究

朱荟吉，齐玉文，徐佳明，邓铁松，金学松*,

边界条件和激励位置对高速列车车窗声振特性影响研究

朱荟吉1，齐玉文2，徐佳明2，邓铁松1，金学松*,1

（1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031； 2.中车长春轨道客车股份有限公司，吉林 长春 130062）

为研究高速列车车窗的振动声辐射和隔声，基于Hamilton原理和声学Rayleigh积分建立了车窗的有限元－边界元耦合模型。利用矩形薄板在自由、简支和固支等经典边界条件下的模态分析结果、无限大板的隔声验证了模型的正确性。基于验证后的模型，对比了车窗在经典边界条件下的声辐射和隔声，分析了点激励位置对车窗声辐射的影响，研究了车窗的隔声随平面声波入射角度的变化规律。研究结果表明，边界条件对车窗在刚度控制区的声辐射和隔声产生显著影响。点激励位置越靠近边界，车窗在刚度控制区的辐射声功率越小；辐射声功率在质量控制区的峰值由车窗的模态引起，由于激励点位置的影响，峰值出现的频率存在一定的差异。随着平面声波入射角度的增加，车窗的隔声量增加；当声波沿车窗的横向和纵向入射时，车窗的受迫响应关于横向中线和纵向中线对称，当声波沿车窗对角线入射时，车窗的受迫响应表现出很强的非对称性。

高速列车；车窗；有限元；边界元；声辐射；隔声

乘客对高速列车乘车舒适度提出了越来越高的要求[1]。高速列车车内噪声是衡量乘车舒适度的重要指标之一[2]。车外噪声源通过激励车窗等车体板件结构振动向车内辐射噪声[3-4]，研究车窗的振动声辐射和隔声对提高乘车舒适度和改善车内声学环境具有重要意义。

国内外学者对高速列车车窗声振特性（振动声辐射和隔声）的研究甚少[5-11]。其中，Baldanzini等[5]建立了由梁和弹性单元连接的两块平行板的波传播理论模型，研究了整体结构的弯曲波在两块板的传递特征，确定了高速列车车窗SEA（Statistical Energy Analysis，统计能量分析）模型关键参数。Yang[6]分别利用声压法和声强测试了高速列车单层车窗隔声，验证了单层车窗AML（Automatically Matched Layer，自适应边界层）隔声计算模型的正确性，基于验证后的模型进一步发展中空充氩双层车窗的隔声模型，结合遗传算法对双层车窗的几何参数进行了优化。张玉梅等[7-8]将高速列车车窗视为双板空腔结构，考虑边界条件的影响，基于波动法和模态叠加法[9-10]，建立了高速列车车窗的隔声模型，通过实测隔声量验证了模型的合理性，掌握了车窗厚度、空腔厚度和空腔阻尼等参数对车窗隔声量的影响规律。Xu等[11]利用SEA对比分析了高速列车单层车窗、双层车窗及中空双层车窗的隔声性能，研究了车窗与窗框间的密封材料对车窗隔声的影响。

除了对高速列车车窗振动声辐射和隔声的研究之外，国内外学者还对高速列车车窗在冲击载荷和脉动压力下的振动响应和疲劳进行了研究[12-14]。

然而，由Zhang等[15]和Yao等[16]对我国高速列车车内噪声的长期跟踪试验和仿真分析可知，车内噪声的主要频段集中在630 Hz左右的中低频。边界条件对高速列车车窗在这个频段的声振特性可能产生显著影响，从而影响车内噪声分布；车窗的隔声可能随入射角度的变化而发生变化；车窗的振动声辐射可能受激励点位置的影响。这些影响因素在以往高速列车车窗声振特性的研究中很少涉及。

因此，本文基于Hamilton原理建立高速列车车窗的FE（Finite Element，有限元）模型；基于声学Rayleigh积分建立车窗两侧流体的BE（Boundary Element，边界元）模型；结合车窗与流体的边界耦合条件，建立车窗的耦合FE-BE声振预测模型。对比经典边界条件下车窗的声辐射和隔声；分析点激励位置对车窗声辐射的影响，研究车窗隔声随平面声波入射角度的变化规律。

1 高速列车车窗的声振预测模型

高速列车车窗的声振预测模型包括车窗的FE振动预测模型、两侧流体的BE声场预测模型及它们的耦合模型。

1.1 车窗的FE模型

高速列车车窗为典型的矩形薄板，以下基于Hamilton原理，利用薄板理论来推导矩形薄板的FE模型。如图1所示，矩形薄板长2（高速列车纵向），宽2（高速列车高度方向，后文中称为横向），坐标系原点位于板中心，面位于板面内，1～4为薄板边界。

图1 矩形薄板示意图

根据Hamilton原理，板的真实位移解所对应的动能与势能之差需满足对任意时段积分的一阶变分等于0：

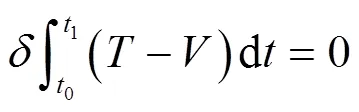
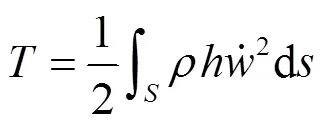
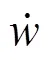
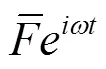
1.2 车窗两侧流体的BE模型

板两侧流体视为无限半空间，场点声压可由经典的声学Rayleigh积分来计算：

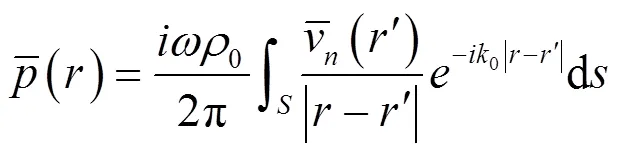
对流体与板相邻的边界划分网格，将式（5）配置于流体边界网格的每个节点，可得流体的BE模型为：

1.3 耦合的FE-BE模型

板在外力激励下（包括平面声波激励和力激励）产生振动，向板两侧声学域辐射声波p1和p2，与两侧流体相互作用。耦合的条件为：

（1）板两侧流体压力作用于板；

（2）板的法向速度与声学域边界的法向速度相等。

结合这两个耦合条件、式（4）和式（6）可得矩形薄板与两侧声学域耦合的FE-BE模型为：

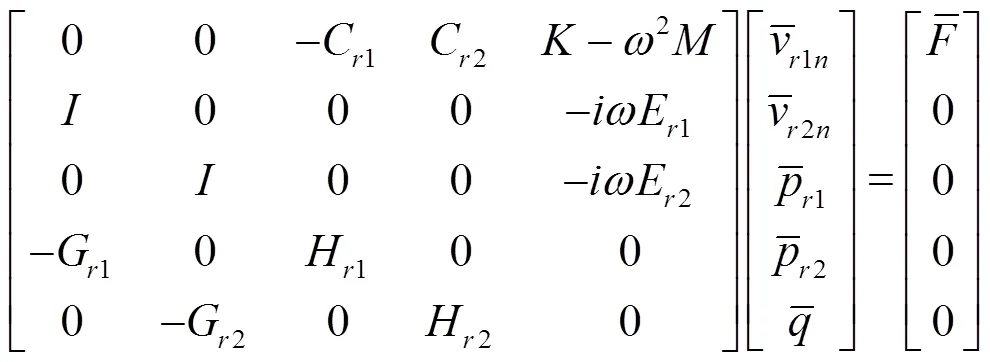
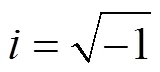
1.4 振动声辐射和隔声

假设平面声波p从声学域1以角度和入射至矩形薄板上，入射角度定义如图2所示。

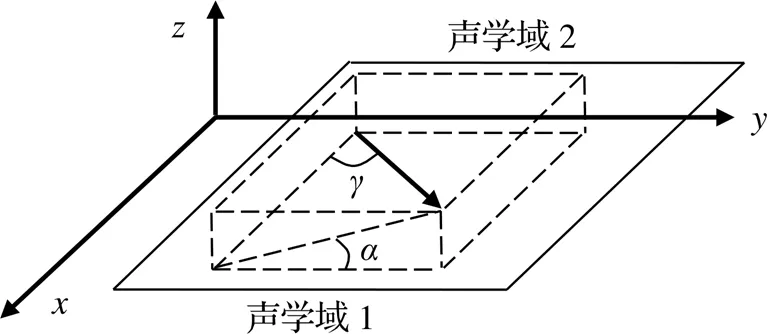
图2 平面入射声波入射角度定义

可知：

将设计图纸变成现实是室内设计最直接的体现，此过程需要相应的施工单位来完成。通常在设计方案完善后，会有很多承包单位进行竞标，发标方会综合考虑竞标单位的实际情况，然后按照自身标准选出实力最强的单位，委托其完成商场建造[2]。在后期施工中，还要做好现场监管、质量评估等多项工作。

由入射声功率和透射声功率可得：

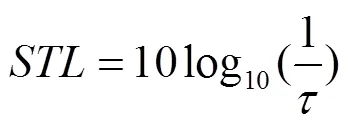
式中：为板在声波以入射角度和入射时的隔声量；为透射声功率与入射声功率之比，即声功率透射系数。

同理，矩形薄板在力激励下，向声学域2中的辐射声功率也可通过式（9）计算。

2 验证

本节以一块长1 m、宽1 m、厚6 mm的铝板ANSYS模态分析结果来验证本文的FE模型，以无限大铝板的隔声来验证耦合FE-BE模型。铝板的材料参数如表1所示。

表1 铝板材料参数

2.1 模态分析

由本文计算的铝板在简支边界条件下的模态频率与ANSYS结果的对比如表2所示（只列出了奇数阶模态）。由表可知，在经典边界条件下，本文得到的模态频率与ANSYS的结果误差在1%以内，本文建立的矩形薄板FE模型准确有效。自由和固支条件下的模态频率误差保持一致，不再赘述。

表2 铝板在简支边界的模态频率对比

2.2 隔声

图3给出了平面声波垂直入射（＝90°和＝90°）时，本文得到的简支和固支边界条件下矩形铝板的隔声量与无限大板结果的对比。由图可知，由于矩形铝板边界刚度的影响，其刚度控制区的隔声比无限大板的隔声大；在质量控制区，矩形铝板的隔声与无限大板的结果整体吻合很好，隔声低谷对应模态频率。

图3 经典边界条件下铝板隔声量与无限大板的对比

通过与ANSYS软件的模态分析结果、无限大板隔声的对比，验证了本文建立的FE-BE模型的正确性，该模型将在下一节用于某型高速列车的声振特性分析。

3 某型高速列车车窗的声振特性研究

某型高速列车车窗如图4所示。由于边界条件只影响结构的低频声振特性，且高速列车车内主要噪声频段在1000 Hz以内[16]，因此，计算的上限频率为1000 Hz。车窗长2＝1 m、宽2＝0.7 m、厚＝4 mm，材料参数如表3。

图4 某型高速列车车窗

表3 某型高速列车车窗材料参数

3.1 振动声辐射

矩形车窗在经典边界条件下，中心在垂向（方向）单位点激励下向板一侧半空间的辐射声功率如图5所示。由图可知，自由边界条件下车窗的辐射声功率与无限大板的结果相似，大小由板的质量决定。随着边界约束刚度的增加，辐射声功率表现出模态特性，峰值对应板的模态频率；在第一阶模态频率之前，辐射声功率主要由板的边界刚度决定（刚度控制区），由于固支比简支约束刚度大，在刚度控制区的辐射声功率比简支小，辐射峰值向高频移动。由于结构模态的影响，简支和固支边界条件下的辐射声功率在第一阶模态频率之后，比自由边界条件下的结果大。

图5 经典边界条件下车窗在中点单位激励下的辐射声功率

为研究激励点位置对结构振动声辐射的影响，将单位垂向力分别布置于图6中的4个点，编号为1、2、3和4，分别位于(0, 0)、(0, -/2)、(-/2, 0)和(-/2, -/2)。

图6 激励点位置示意图

在这四个激励点下的辐射声功率对比如图7所示。由图可知，辐射声功率的第一个峰值（30 Hz处）由矩形车窗的第一阶模态引起，四个激励点均能激发这阶模态。在四个激励点下，30 Hz处的车窗变形情况如图8所示，车窗在这四个点激励下的振动响应相似，但幅值存在一定的差异：激励点1位于矩形车窗的正中，车窗变形最大；激励点2和激励点3靠近窗框，刚度更大，它们对应的车窗变形要小于激励点1；激励点4引起的车窗变形最小。

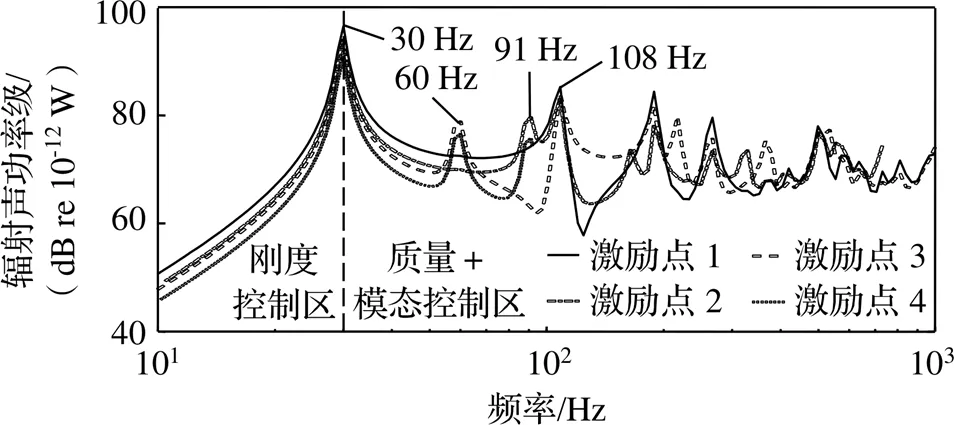
图7 简支边界条件下激励点位置对辐射声功率的影响

由图7还可知，当频率小于30 Hz（第一阶辐射峰值之前）时，由于结构的辐射声功率由结构的刚度决定，激励点1对应的辐射声功率最大，然后依次是激励点2、激励点3和激励点4；当频率大于30 Hz时，结构的辐射声功率由结构的质量决定，因此，四个激励点下的辐射声功率大体趋势保持一致；由于激励点位置对结构的固有模态是否被激发产生决定性的作用，所以在这四个激励条件下，它们的声功率辐射曲线会产生一些波动和峰值，峰值出现的位置可能一致，也可能产生差异。例如，激励点3和激励4在60 Hz处产生的辐射峰值是由结构的纵向第二阶模态引起的，它们在该频率下车窗的变形相似，如图9所示，由于激励点3恰好位于该模态波腹的位置，其产生的变形稍大；激励点1和激励点2刚好位于第2阶模态波节的位置，模态未被激发，导致在该模态频率下，它们的辐射声功率未产生峰值。

同理，在图7中91 Hz处，激励点2和激励点4能产生辐射峰值，而激励点1和激励点3未产生峰值。

图8 四个点激励下30 Hz对应的车窗变形

图9 激励3和4下60 Hz对应的车窗变形

3.2 隔声量

图10给出了在平面声波垂直入射下，车窗在四边自由、简支及固支时的隔声量对比。由图可知，四边自由车窗的隔声曲线随频率的变化规律与无限大板的结果类似，满足质量隔声定律。由于车窗四周边界条件引起结构刚度的变化，固支边界条件下的刚度区隔声量和各阶隔声低谷频率均比简支边界条件大。在质量控制区（频率大于约300 Hz），简支和固支条件下的隔声量除了在隔声低谷附近频带外，与自由边界条件下的隔声量保持一致，这进一步说明本文建立的FE-BE模型的正确性。

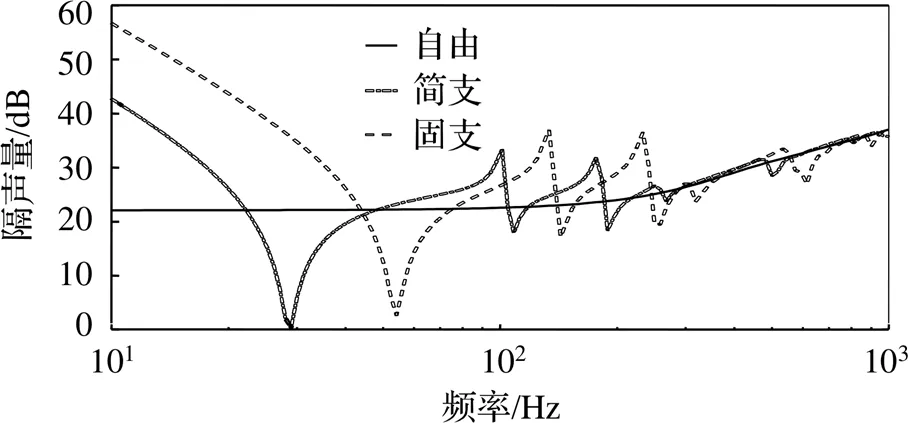
图10 经典边界条件下声波垂直入射隔声量的变化情况

在简支条件下，平面声波入射角度对高速列车车窗隔声的影响分为三种情况：①沿横向斜入射；②沿纵向斜入射；③沿车窗对角线斜入射。结合图2可知，当声波沿横向斜入射时＝90°，声波矢量与车窗的夹角为；当声波沿纵向斜入射时，＝90°，声波矢量与车窗的夹角为；当声波沿车窗对角线斜入射时，声波矢量与车窗的夹角为＝sin-1(sinsin)。三种声波入射条件下，分别计算了波矢量与车窗所在平面的夹角为30°、50°和70°三种情况下的隔声。

声波沿横向入射时，车窗隔声量随入射角度的变化情况如图11所示，为方便比较，声波垂直入射的隔声量也画于图中。由图可知，随入射角的增加，车窗的隔声量逐渐变大，这是因为入射角度越大，声波矢量在车窗平面的分量越小，即声波在车窗平面表现出的波动越不明显，越难与车窗的结构波耦合向另一侧辐射声能量。斜入射下88 Hz和329 Hz处的隔声低谷频率未出现在垂直入射下的隔声曲线上，且随入射角度的增加，这些频率的隔声低谷逐渐变小直至垂直入射时的消失。原因如图12所示：当声波沿横向入射且角度很小时，很容易激起结构沿横向的第四阶模态；值得注意的是，由于声波与结构的耦合，车窗的实际变形与车窗在自由状态下的模态振型存在一定差异，结构的实际变形呈现出沿波前方向挤压的特征，即车窗在声波波前的振动响应比波后大；随着入射角度的增加，车窗振动响应变小，所以329 Hz处隔声低谷逐渐变小；当入射角度增大至垂直入射时，车窗的振动响应出现明显变化，表现出更复杂的振型，且响应很小，所以在垂直入射条件下，车窗在329 Hz处未出现隔声低谷。

图11 简支边界条件下入射角α对隔声的影响（γ＝90°）

图13给出了简支边界条件下，声波纵向斜入射时，入射角度对车窗隔声的影响。与声波沿横向入射的情形相似，随着入射角度的增加，隔声量逐渐变大。斜入射条件下车窗隔声曲线在58 Hz、176 Hz、217Hz等频率点出现了低谷，在垂直入射条件下未出现。这是因为在这些频率点，车窗在斜入射下的振动响应较垂直入射大，且在纵向表现出了明显的模态特征，如图14所示。

综合图12和图14还可知，当声波沿纵向或横向斜入射时，车窗的振动响应分别关于轴（车窗纵向中线）或轴（车窗横向中线）对称。

由图15可知，与图11和图13类似，随着入射角度的增加，隔声量变大；与它们不同的是，垂直入射条件下的隔声量与其他三种情况基本一致。值得指出的是，由于车窗长和宽不相等，声波沿对角线方向斜入射时，车窗的振动响应表现出很强的非对称性，不关于纵向、横向和对角线方向对称，这种非对称性随着入射角度的增加而减弱。如图16所示，当入射角度为30°和50°时，车窗的振动响应非对称性很强，大于0区域的振动峰值明显比小于0区域的大，且声波波前的峰值明显比波后的振动响应强；当入射角度为70°时，车窗振动响应的非对称性明显减弱；当垂直入射时，车窗振动响应可近似用横向第三阶模态振型来描述。

4 结论

本文以高速列车车窗为研究对象，建立了车窗FE-BE声振预测模型。对比了经典边界条件下车窗的声振特性，分析了点激励位置对车窗声辐射的影响，研究了隔声随平面声波入射角度的变化规律。

图12声波沿横向入射时329 Hz对应的车窗变形情况

研究结果表明：

（1）本文得到的模态分析结果与ANSYS吻合很好；本文得到隔声与无限大板的结果在质量控制区吻合很好，本文建立的FE-BE模型对于研究高速列车车窗的声振特性准确有效。

（2）边界条件对车窗的声辐射和隔声影响显著。边界约束刚度越强，刚度控制区声辐射越小，隔声量越大；质量控制区声辐射峰值或隔声低谷随边界约束刚度的增强向高频移动。

（3）点激励位置对车窗的声辐射影响很大。激励点越靠近边界，其在刚度控制区的声辐射越小；当激励点远离模态振型波节时，该模态才容易被激发，出现声辐射峰值。

（4）随着平面声波入射角度的增加，车窗的隔声量变大。当声波沿纵向或横向斜入射时，车窗的动态响应关于车窗的纵向或横向的中线对称；当声波沿车窗对角线入射时，车窗的振动响应表现出很强的非对称性。

图14 声波沿纵向入射时176 Hz对应的车窗变形情况

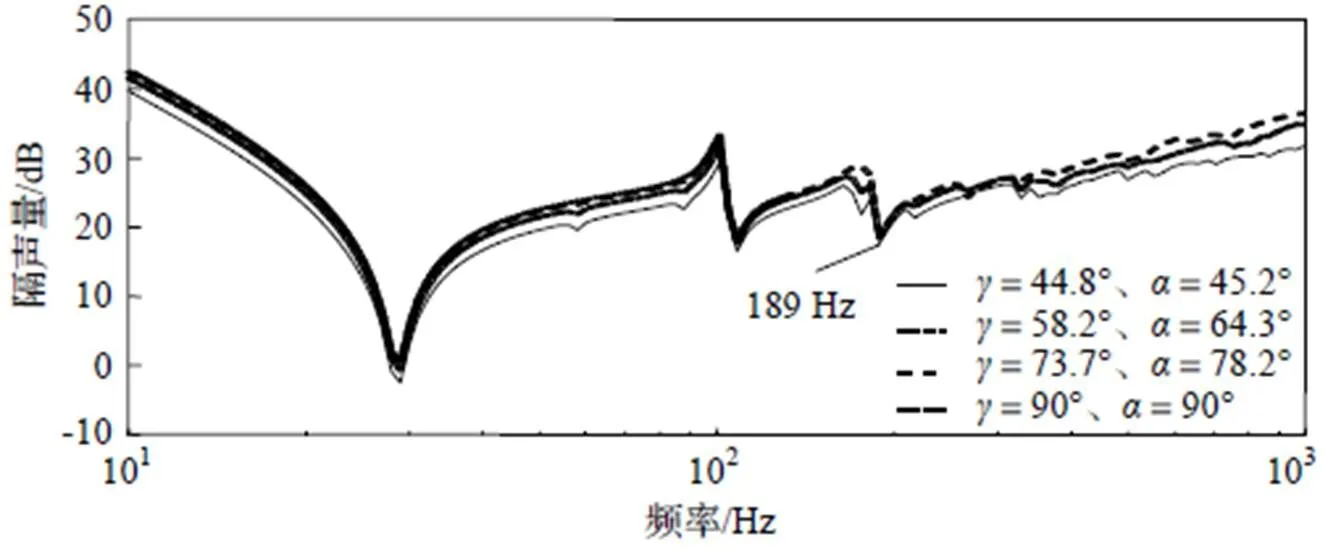
图15 简支边界条件下入射角θ（声波沿车窗对角线斜入射）对隔声的影响

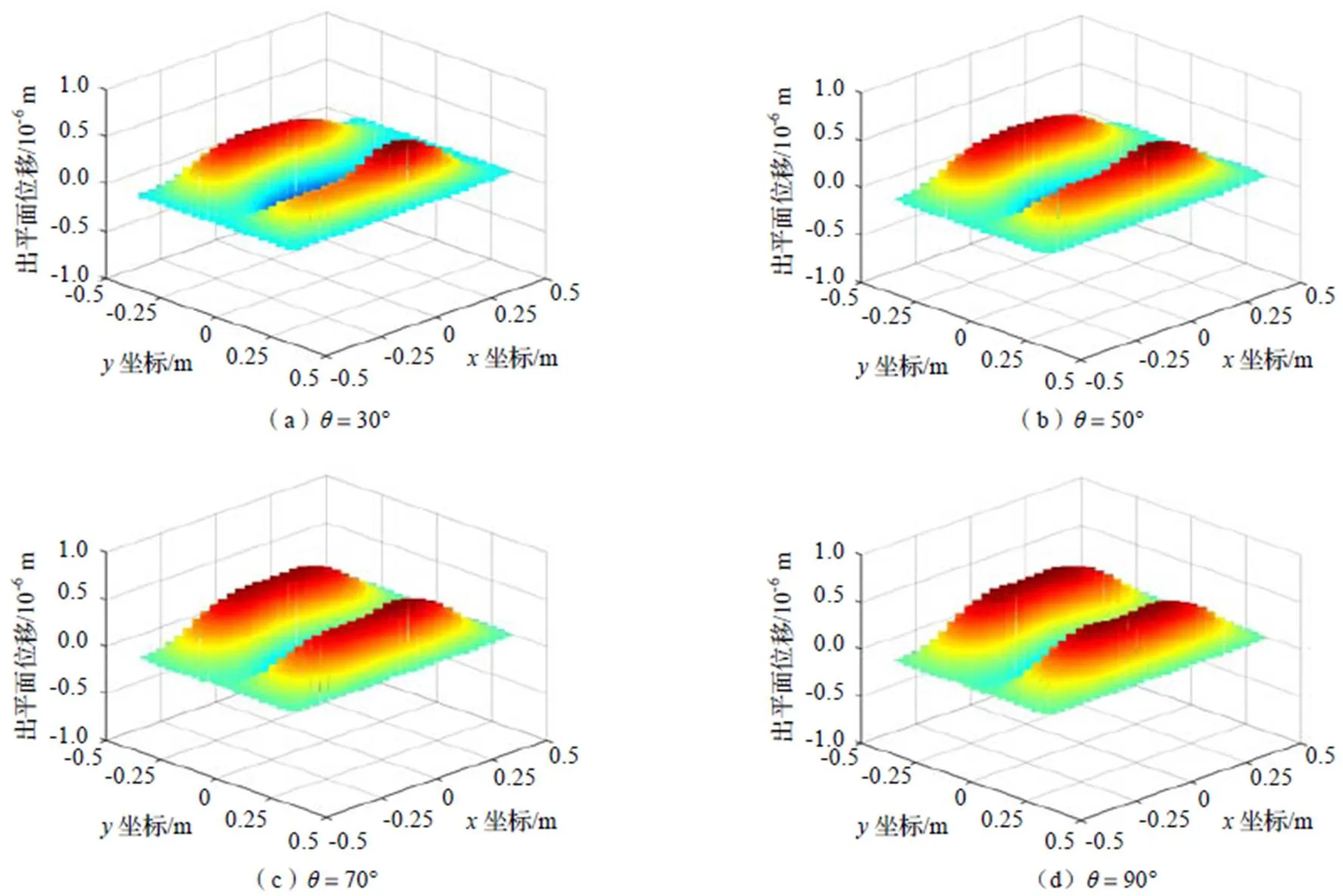
图16 声波沿车窗对角线入射189 Hz对应的车窗变形情况

[1]Jin XS. Key problems faced in high-speed train operation[J]. J Zhejiang Univ Sci A，2014（15）：936-45.

[2]张捷. 高速列车车内低噪设计方法及试验研究[D]. 成都：西南交通大学，2018.

[3]李明，韩铁礼，朱荟吉，等. 高速列车组合地板结构隔声性能分析 [J]. 机械，2020，47（10）：60-65.

[4]张传英，张继业. 基于仿生形态的高速列车气动性能研究[J]. 机械，2019，46（4）：42-47.

[5]Baldanzini N，Pierini M，Scippa A. SEA modeling of an high speed train window[C]. International Conference on Noise and Vibration Engineering，Catholic University of Leuven Press，2002：765-773.

[6]Yang Li. Numerical optimization of sound insulation performance for the new type glass window based on genetic algorithm and its application in high-speed trains[J]. Journal of Vibroengineering，2016（18）：606-621.

[7]Zhang YM，Xiao XB，Thompson DJ. Sound transmission loss of windows on high speed trains[C]. 13th International Conference on Motion and Vibration Control，IOP Publishing Ltd.，2016：012141.

[8]张玉梅，王瑞乾，李晔，等. 高速列车车窗隔声量研究[J]. 机械工程学报，2018，54（2）：212-221.

[9]Xin FX，Lu TJ，Chen CQ. Vibroacoustic behavior of clamp mounted double-panel partition with enclosure air cavity[J]. Journal of the Acoustical Society of America，2008，124（6）：3604-3612.

[10]Xin FX，Lu TJ，Chen CQ. Sound transmission through simply supported finite double-panel partitions with enclosed air cavity[J]. Journal of Vibration and Acoustics，2010，132（1）：011008.

[11]Xu ZX，Shi GT，Diao XG，et al. Research on control effect of window glass on inner sound environment of high-speed train[C]. 2019 IEEE International Conference on Mechanics and Automation，IEEE，2019：240-245.

[12]Jing L，Liu K，Ren M. The transient response of car body and side windows for high-speed trains passing by each other in a tunnel [J]. Composites Part B-Engineering，2019（166）：284-297.

[13]Jeon CS，Kim YG，Park TW. A study on impact damage characteristics of the window glass for high speed train[J]. Journal of the Korean Society for Railway，2012，15（3）：217-233.

[14]钱春强，郑志军，虞吉林，等. 高速列车侧窗受交会压力波作用的动态响应 [J]. 机械工程学报，2013，49（9）：30-36.

[15]Zhang J，Xiao XB，Sheng XZ，et al. SEA and contribution analysis for interior noise of a high speed train[J]. Applied Acoustics，2016（112）：158-170.

[16]Yao Dan，Zhang Jie，Wang Ruiqian，et al. Vibroacoustic damping optimisation of high-speed train floor panels in low- and mid-freqeuency range[J]. Applied Acoustics，2021（174）：107788.

Effect of Boundary Conditions and Excitation Location on Acoustics and Vibration Characteristics of High-Speed Train Windows

ZHU Huiji1，QI Yuwen2，XU Jiaming2，DENG Tiesong1，JIN Xuesong1

( 1.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China; 2.CRRC Changchun Railway Vehicles Co., Ltd., Changchun 130062, China)

In order to study the acoustics and vibration characteristics of a high-speed train window, the coupling finite element and boundary element (FE-BE) model of the window is established based on Hamilton principle and Rayleigh integral. The FE-BE model is verified by comparing the results with the modal analysis of a rectangular plate subject to classical boundary conditions and the sound transmission loss (STL) of an infinite plate. Using the FE-BE model, the STL and sound radiation (SR) of the window under the classical boundary conditions are compared. The effect of the point force location on SR of the window is analyzed. The influence of the incident angle of an acoustic plane wave is investigated. The results show that boundary conditions significantly affect the SR and STL of the window in the stiffness controlling region. When the point force moves to the boundary, the corresponding SR in the stiffness controlling region decreases. The SR peaks in the mass controlling region is attributed to the modal behaviour of the window. Increasing the incident angle of an acoustic plane wave can enhance the STL of the window. The dynamic response of the window is symmetric about the midline of the window when the acoustic plane wave obliquely impinges on the window in the longitudinal and lateral directions. However, it shows a strong asymmetry when the acoustic wave impinges along the diagonal direction of the window.

high-speed train；window；finite element method；boundary element method；sound radiation；sound transmission loss

U270.1+6

A

10.3969/j.issn.1006-0316.2021.09.008

1006-0316 (2021) 09-0050-10

2021-01-20

国家自然科学基金（U1934203）

朱荟吉（1995－），女，江苏无锡人，硕士研究生，主要研究方向为高速列车板件结构的振动噪声，E-mail：760551262@qq.com。

通讯作者：金学松（1956－），男，江苏扬州人，博士，教授，主要研究方向为轮轨关系和伤损、轨道交通振动噪声与控制，Email：xsjin@swjtu.edu.cn。