例谈数形双视角解决向量的夹角问题

顾予恒

(浙江省杭州第二中学钱江学校 311215)

向量的夹角是向量概念中的一大要素，是刻画两个向量之间相对位置关系的重要量.近年来，它已成为向量考查的重要知识点之一.向量的夹角既有明显的几何特征，又与数量积运算有着密切的联系，因此也是培养学生数形结合思想的重要阵地.

一、代数视角，公式运算

例1已知非零平面向量a,b满足|a|=2|b|，且(a-b)⊥b，则a,b的夹角为( ).

解析由(a-b)⊥b，得(a-b)·b=0.

即a·b=b2，即|a|·|b|cosθ=|b|2.

点评向量的数量积运算中蕴含夹角余弦值，因此通过向量的代数运算，可以方便地求出夹角.

例2 非零向量a,b满足2a·b=a2·b2，|a|+|b|=2，则a与b的夹角的最小值是____.

解析由(|a|+|b|)2=4,得|a|2+|b|2=4-2|a|·|b|≥2|a|·|b|，即|a|·|b|≤1.

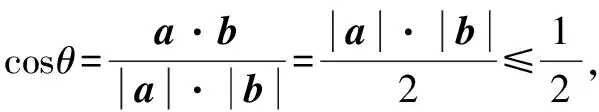
例3 设向量e1,e2满足|e1|=2,|e2|=1，e1,e2的夹角是60°，若2te1+7e2与e1+te2的夹角为钝角，则t的取值范围是____.

解析因为2te1+7e2与e1+te2的夹角为钝角，故(2te1+7e2)·(e1+te2)<0，且2te1+7e2与e1+te2不反向共线.

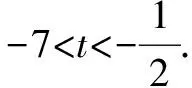
点评两个向量成锐角或钝角，与数量积为正或为负有关，但不是充要条件，要注意共线的特例，往往是利用共线条件进行剔除.

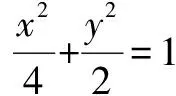
解析设P(x,y)，则Q(x,-y).

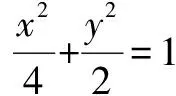
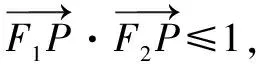
点评建系条件下的向量夹角坐标表示形式也是求解夹角的一种有力工具.

分析本题看似是一道三角函数的问题，但其研究的对象是三角形的三个角，那么如何使用向量方法来刻画三角形三个内角的余弦值呢？

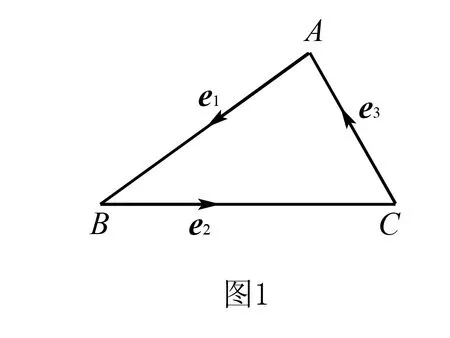
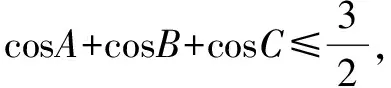
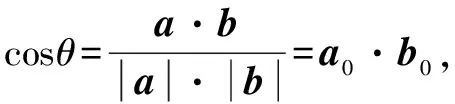
二、几何视角，图形探究

如果能利用向量的几何表示作出图形，那么用平面几何的知识也能帮助探求夹角.

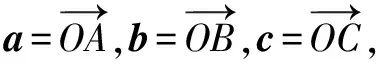
点评本题是用向量刻画了米勒问题(山高模型)中的仰角差，教材中的计算山高、塔高的问题就是这类问题的现实模型.在直角三角形中，利用仰角的正切值来研究仰角差比较便利.

例7 已知平面单位向量a,b满足a·b=0，记f(x)=tan〈b+xa,b+(x-1)a〉，则f(x)的最大值为____.

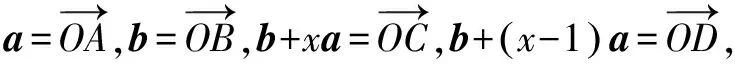
图4 图5

(1)如图4，当点C和点D在点B的同侧，设BC=x≥1，BD=x-1，则tan∠BOC=x，tan∠BOD=x-1.

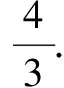
点评本题是例6的进化版，用向量刻画了平行线上的两等距离动点，研究向量的夹角，实质还是仰角差模型的应用，但要注意有两种情况分类讨论.

例8 已知平面向量a,b,c满足|c|=4，a·(c-a)=b·(c-b)=3，当a与b的夹角最大时，a·b=____.

分析注意到题干条件a·(c-a)=b·(c-b)=3是同构式，刻画的是同一个圆.

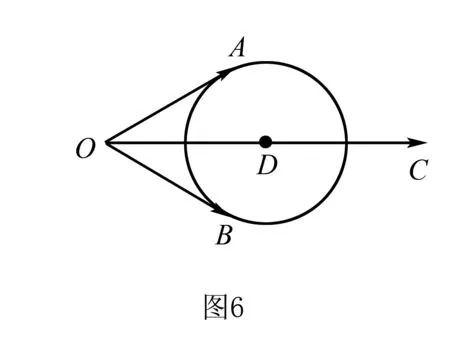
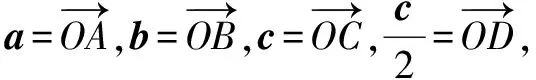
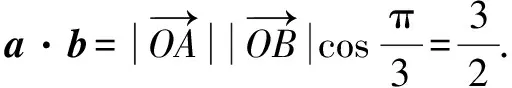
点评本题用向量刻画了一个几何知识点，即圆外一点与圆上两点连线的夹角最大为切线角，将问题转化为求圆外一点与圆心连线距离最短.

例9 已知平面向量a,b,c,e满足|a|=4，|b|=|c|=2,|e|=1，则tan〈a+b+e,a+c+e〉的最大值是____.

分析注意到要求的角〈a+b+e,a+c+e〉中有共同的元素a+e，故视为整体.

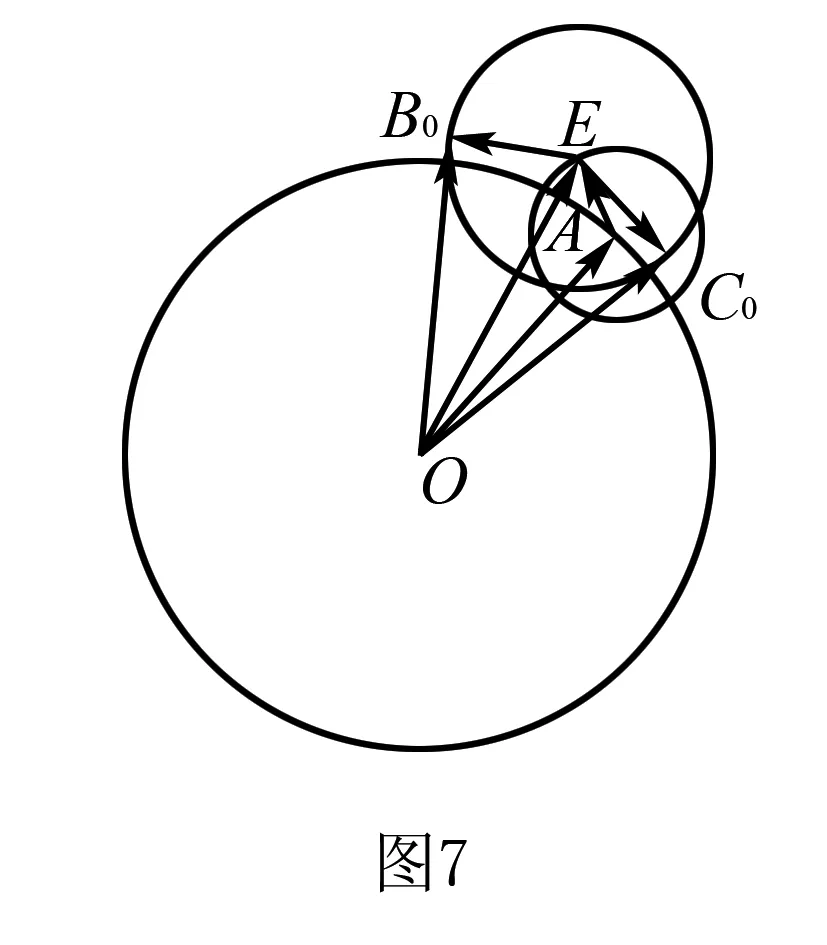
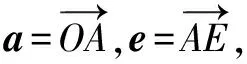
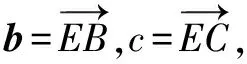
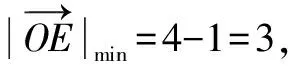
点评本题是例8的升级版，考点依然是圆的切线角最大，但对向量几何作图提出了更高的要求.

三、数形结合，比翼齐飞

灵活运用代数与几何多角度研究夹角问题，有助于培养学生数形结合的思想方法，提升数学运算和直观想象的核心素养.

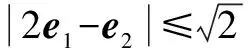
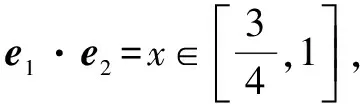
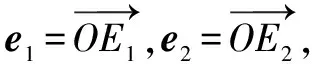
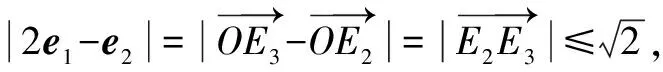
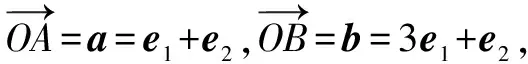
记E2(x,y)，则由山高模型知，

要求cos2θ的最小值，即求tanθ最大时的θ值.

至此，向量的夹角问题得到了很好的解决.向量作为数形结合的主阵地，处理问题的方法一般也有代数的数量积运算与几何的图形背景两个角度.在日常的教学和学习中，只有不断加强两方面的研究，才能在数与形之间自由切换，收放自如.