平面向量的几类运算问题

巨小鹏

(陕西省汉中市龙岗学校 723102)

平面向量是代数、几何和三角函数之间的桥梁，集数与形于一体的一种工具.从向量的运算角度看，向量具有较好的代数结构；从几何角度看，向量是空间最基本原始的几何量.这使得向量运算都有着其几何意义，运算律也具有丰富的几何内涵，如向量的加法用几何语言描述就是三角形法则或平行四边形法则；向量加法的交换律是平行四边形定理的向量表述形式；数乘运算的分配律是相似三角形定理的代数形式；数量积的分配律也是勾股定理代数化的一种表达形式等.平面向量运算内容包括平面向量的加减运算、数乘运算、数量积、向量的模、运算法则、运算性质和几何意义等.

一、 图形形式的运算问题

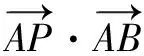
A.(-2,6) B．(-6,2) C．(-2,4) D．(-4,6)

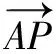
分析3 坐标法也可以，较简单在此不赘述.

评析以正六边形为载体，考查有关平面向量数量积的取值范围，涉及到的知识点有向量数量积的运算及其几何意义.

二、符号形式的运算问题

评析考查了利用模求向量数量积、利用向量数量积求向量夹角、利用函数单调性求最值，考查转化与化归思想，考查数学运算、数学建模等学科素养，解题关键是合理转化，应用函数求最值，特别注重基础.

三、坐标形式的运算问题

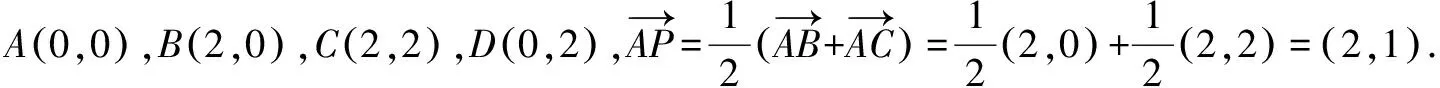
评析考查平面向量的模和数量积的计算，建立平面直角坐标系，求出点P的坐标是解答的关键.

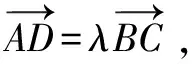
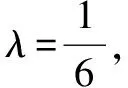
评析考查平面向量数量积的计算，考查平面向量数量积的定义与坐标运算.坐标法明显比较好，运算更加流畅，也容易想到.

四 、平面向量与平面几何的综合问题

A．8 B．6 C．4 D．2

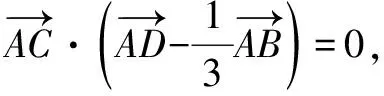
不管哪种类型的题，方法的选取无非就是定义法、基向量法、坐标法、几何意义法，必要的时候构造方程、构造三角形、解三角形等.在学习过程中更要重视一题多解和一解多题的反思性总结.