ID3决策树在预测电解槽出铝量中的研究与实现

孙长好,王 健,杨 飞,姜海超

(内蒙古霍煤鸿骏铝电有限责任公司，内蒙古 霍林郭勒 029200)

现代大型铝电解槽一种多相-多场交互作用下的复杂电化学反应器[1],具有非线性、大时变、大时滞和多输入多输出的特点[2]，且不能建立精确的数学模型[3]。电解槽的各种工艺参数的调整往往凭借专业管理者的主观经验，依赖人工进行槽况判断、趋势分析和运行操作决策，其经验水平往往决定了策略的正确性。传统的人工控制决策方式已经难以适应现代铝电解生产要求[4]，知识自动化是铝电解槽实现寻优决策的必由之路，应用机器学习技术，建设工业大数据分析平台，充分挖掘数据潜在价值，将铝电解数据库中包含的专家知识和经验进行知识表示和自动推理，模拟管理者的决策过程，本文将ID3决策树应用于铝电解槽出铝量预测，对于辅助工艺管理人员做出科学的决策，提高生产智能管理水平具有现实意义。

1 ID3决策树分类算法的基本思想

1.1 ID3算法的基本思想及实现

Ross Quinlan在CLS学习算法的基础上，提出ID3决策树概念。作为一种机器学习方法，ID3算法着眼于从一组无次序、无规则的事例中推理出决策树表示形式的分类规则。采用自顶向下递归的贪婪算法构造。从根结点开始，以样本集的最大信息增益属性作为启发搜索条件，将数据样本划分成不同的样本子集，每个样本集构成新生分裂节点，对该分裂结点继续向下遍历属性，不断递归调用，仅当下列条件之一成立时返回：

(1) 节点上的样本集属于同一类；

(2)没有用来进一步划分样本的属性。

生成决策树的每个叶子即对应一个决策分类, 因此，从根到叶节点的一条路径就对应着一条合取规则，整棵决策树就对应着一组析取表达式规则。生成决策树实现流程如图1所示。

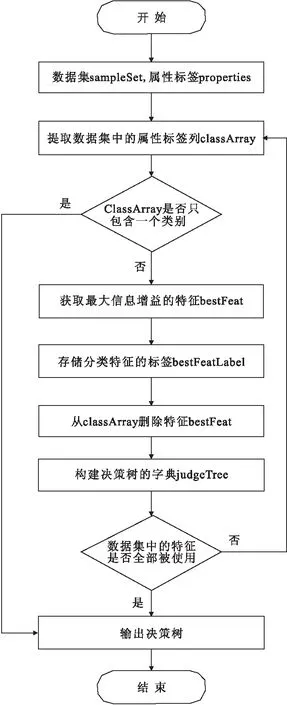
图1 ID3决策树算法流程图

1.2 信息增益标准

Ross Quinlan提出以信息熵的最速下降作为选择测试属性的方法，该属性能反映出分类样本中的信息量最小，具有最小的随机性，这使得对一个对象分类所需的期望测试数目达到最小，并确保找到一棵简单的决策树。

设S是s个训练样本的集合，包含m个不同的属性，从而定义了m个不同的类Ci(i=1,...,m),si是S中属于类Ci的样本个数。以熵的概念来定义样本集的信息量：

其中，pi是样本属于类Ci的概率，并用si/s估算。

设属性A具有v个不同值{a1,a2,...,av}，可以把S划分成v个子集{s1,s2,...,s}，如果A被选为测试属性，则这些子集对应于包含集合S的节点上生长出来的分枝。设sij表示在子集sj中类ci的样本数，那么，根据属性A分类的子集的熵为：

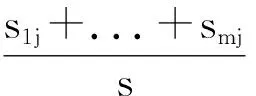
使用属性A对样本集S进行分类所获得的信息增益计算方法是：

Gain(A)=1(s1+...+sj)-E(A)

用样本集的总信息熵减去属性A的每个分支的信息熵与权重的乘积，通常，信息增益越大，意味着用属性A进行划分所获得的决策确定性越大。

众多学者对ID3决策树做了深入改进研究，文献[5]将粗糙集理论用于决策树算法的属性选择标准，文献[6]、[7]针对静态分类规则的缺陷，展开动态数据样本集决策树研究，文献[8]提出了一种加权的决策树算法，通过引入属性权值参数∂，强化重要属性。

Gain(A)=1(s1+...+sj)-∂E(A)

文献[8]中作者对权值的设定并没有具体的依据，只是根据假设来人为的设定权值。结合电解铝的生产工艺，提出一种改进的ID3算法，应用回归分析计算各条件属性影响出铝量的权重W1,W2,...,Ws(s表示条件属性的个数)，然后通过Wi来求解各∂i。

使用Python语言实现算法如下：

# 计算信息熵

def calcEntropy(sampleSet):

numSample = len(sampleSet)

PropCounts = {}

# 样本遍历

for sample in sampleSet:

currentProp = sample[-1]

if currentProp not in PropCounts.keys():

PropCounts[currentProp]= 0

PropCounts[currentProp]+=1

entropy = 0.0

for key in PropCounts: # 计算信息熵

probability = float(PropCounts[key]) / numSample

entropy = entropy - probability * log(probability, 2)

return entropy

2 数据预处理

表1的铝电解原始数据无法直接应用于ID3算法，需要首先进行数据的规范化处理，主要包括数据校正和离散化过程。

表1 3031#电解槽原始数据

2.1 数据校正

铝电解控制系统在进行采样时，由于网络堵塞丢帧或者人工输入时失误导致数据序列出现异常值，处理办法主要有二种，一是采用过滤的方法，将含有异常数据的记录丢弃，该种方法处理简单，但会失去部分信息；二是使用插值算法，其思想是：铝电解过程是一个缓慢的变化过程，可根据系统运行的惯性，参考空值前后的数据进行分析填补。

2.2 数据离散化

在铝电解生产工艺中，影响出铝量的主要因素有：日平均电压(AvgVol)、分子比(Ratio)、电解质水平(Bath_H)、铝水平(Metal_H)，电解质温度(Temp)等，这些原始数据是连续的，无法直接应用于ID3算法，因此，有必要将其转换成适合数据挖掘的形式，本文采用直方图的策略进行数据离散化。

直方图是一种直观的数据归约形式。将属性数据分布划分为不相交的子集，该子集的高度或面积代表属性值的平均频率，一般地，确定属性值的划分有以下几种方法：

等高：在等高的直方图中，每个子集的频率区间是一个常数，即临近数据样本个数相同。

等宽：在等宽的直方图中，每个子集的宽度区间是一个常数，通常，数据离散化处理后会得到一些空数据区间，生成决策树的过程中会丢失一定的规则，因此，应当对这些空数据区间进行前后合并，表2是经等宽离散化处理后所生成电解槽序列化数据。

表2 3031#电解槽离散化数据

3 产生决策树

对某工区31台电解槽近半年的数据预处理，选择日平均电压(AvgVol)、分子比(Ratio)、电解质水平(Bath_H)、铝水平(Metal_H)，电解质温度(Temp)作为影响出铝量(Metal_Mass)的5个条件属性，分别进行粒度为98 mV，0.08，21 mm，22 mm，6 ℃和53 kG的等宽离散化处理，生成序列化数据表示，经ID3算法评判后构造出铝量决策树，如图2所示，由于生成的出铝量决策树规模较大，图中仅绘制出温度序列为7和2的出铝量决策分枝。

图2 出铝量决策树

图中分枝Temp(7) -> Metal_H(7) -> AvgVol(2) -> Bath_H(6) -> 26表示：当电解质温度在[991,997] ℃，铝水平在[322,344] mm，日平均电压在[3953,4051] mV,电解质水平在[200,220] mm时，出铝量决策范围应为[3018,3071] kG。

从该决策树中可见，在某些情况下，5个条件属性并非都对出铝量产生决定影响，甚至其中的2个条件属性就可以决策出铝量，如Temp(2) -> Ratio(3) ->32表示：当电解质温度在[961,967] ℃，分子比在[2.41,2.49]时，出铝量决策范围应为[2859,2912] kG，出现这种情况的原因在于数据样本的不完备性，从而出现决策的近似表达，随着电解槽数据的日积月累，数据样本趋于完备，机器学习的广度和深度逐步加深，决策的表达会趋于精确。

4 结 语

利用ID3算法对铝电解数据库中包含的专家知识和经验进行知识表示和自动推理，从而生成出铝量决策规则，对于辅助工艺管理人员做出科学判断提供决策支持，同理，也可应用于电解槽管理其它方面，以提高生产智能管理水平。