分层排土场边坡降雨入渗过程及稳定性分析

蔡文倩，王建德，姜立春

(1.华南理工大学 安全科学与工程研究所，广州 510640；2.广东省安全生产科学技术研究院，广州 510060)

连续强降雨是矿山排土场边坡工程地质灾害的主要诱因，降雨入渗是排土场边坡失稳的主要诱因[1]。岭南沿海地区雨量充沛，降雨时间短、强度大，对排土场边坡稳定性的影响更加复杂。分层碾压排土是提高矿山排土场边坡稳定的主要措施[2]，在降雨作用下，土体体积含水率的增加容易增大介质颗粒的下滑力，极易造成边坡整体失稳[3-5]，因此，开展降雨入渗条件下土体内体积含水率与降雨入渗深度的变化，对分层排土场边坡稳定性研究，具有十分重要的意义。

长期以来，国内外学者主要从降雨入渗过程[6-8]和安全系数[9-11]两个方面，开展降雨作用下边坡稳定性影响研究。在降雨入渗过程方面[6-8]，王文焰等[6]将饱和层与传导层统一视为饱和区，推导出适用于黄土土体的积水入渗模型，描述非饱和黄土中的水分入渗过程。MA等[7]引入饱和系数来确定湿润区的含水量和导水率，基于Green-Ampt入渗模型，较好地揭示了均质土体的入渗速率、累积入渗量和湿润锋的运动过程。张杰等[8]针对黄土入渗水分剖面变化特征，基于达西定律和雨水入渗质量守恒方程，推求入渗深度和时间的模型关系。在边坡安全系数方面[9-11]，WANG等[9]针对常用条分法分析边坡稳定性存在的缺陷，提出了一种基于条带之间几何关系的土质边坡可靠度分析和安全系数计算方法。王奭[10]采用有限元极限分析方法结合强度折减理论，定义无量纲参数P，求解边坡安全系数，判定均匀土质边坡稳定性。ARYA等[11]采用数值模拟方法，研究给出孔隙水压力与裂缝位置对边坡安全系数的影响关系。总体而言，相关研究主要集中于对单层均质土坡的研究，鲜有涉及降雨入渗条件下分层排土场边坡的问题。

本文拟采用分层边坡降雨入渗深度计算方法，结合土力学试验，研究不同降雨条件作用下，岭南某露天矿山分层排土场边坡的体积含水率、入渗深度以及安全系数等变化过程，分析其稳定性，利用现场监测数据，验证分析结果的可靠性，为降雨入渗分层边坡的灾害防治提供理论依据。

1 理论计算

1.1 分层边坡降雨入渗深度Hf

对于降雨入渗诱发分层结构边坡失稳而言，滑裂面通常出现在不同土(岩)层的交界面区域。究其原因，当湿润峰(湿润峰是指水分下渗过程中，土壤被湿润的先头部位与干土层形成的明显交界面)下移至分层交界面时，由于各分层土(岩)间渗透系数不同，容易在交界面区域出现土体饱和问题，进而产生滑移现象诱导边坡发生失稳破坏。

研究表明[12-14]，要研判土(岩)质边坡破坏模式与分布位置，关键是要确定雨水的入渗深度，雨水的入渗深度是由土体的渗透系数决定，因此研究降雨条件下土体渗透系数对入渗深度的影响是评价边坡稳定性的重要方面。图1为根据矿山排土场现状地形图和原始地形图建立典型剖面得到的分层边坡模型。其中，(a)为排土场边坡实景图，(b)为排土场边坡剖面图，(c)为降雨条件下分层边坡体积含水率θs分布示意图。

在图1(c)中：L1，L2分别为不同土层的垂直厚度；θ1i、θ2i、θ3i分别为土层1、土层2、强风化岩的初始体积含水率；θ1s、θ2s、θ3s分别为不同土层的饱和含水率；Δθ1，Δθ2，Δθ3分别为设定的不同分层土体内饱和含水率与初始含水率的差值。

1.1.1 降雨入渗两层边坡深度

1)当降雨强度q小于渗透系数K1，且湿润锋位于土层1时，湿润锋到达土层1、2交界面的时间t1为：

(1)

此时，降雨入渗的深度Hf为：

(2)

2)当降雨强度q大于渗透系数K1，且湿润锋位于土层1时，湿润锋到达土层1、2交界面的时间t1为：

(3)

此时，降雨入渗的深度Hf为：

(4)

1.1.2 降雨入渗多层边坡深度

同理可得，湿润锋到达第i，i+1土层交界面的时间和降雨入渗深度。

1)当降雨强度q小于i土层的渗透系数Ki时，根据式(1)分别计算雨水在不同土层中的入渗时间t1，t2，t3，…，ti-1，再结合式(2)计算湿润锋到达第i，i+1土层交界面的时间ti，即为：

(5)

由式(5)得到湿润锋到达第i、i+1土层交界面的时间ti。将计算结果代入式(2)，可得降雨入渗深度Hf。

(6)

2)当降雨强度q大于第i土层渗透系数Ki，且湿润锋位于第i土层中，同理可得湿润锋到达第i、i+1土层交界面的时间ti和降雨入渗深度Hf。

(7)

(8)

1.2 分层边坡安全系数F

对于多层结构土质边坡而言，降雨条件下由于不同土层的渗透系数不同，雨水到达土层交界面时易产生饱和区，边坡易发生失稳破坏，因此亟需对土层交界面处的安全系数进行监测。

在利用有限元法分析边坡稳定性时，常可通过模型计算的收敛性来判断。如果模型计算收敛，则表征该边坡模型在此工况下处于稳定状态，反之，如果模型计算不收敛，则处于不稳定状态。通过调整参数可使有限元计算从收敛变得不收敛，就反映了边坡模型从稳定状态向不稳定状态的转变。强度折减就是把土体的抗剪强度值c，φ值和折减以后的土体强度值c′，φ′值代入有限元中计算，并不断变换折减系数，直到计算达到收敛状态，即为所求的安全系数F：

F=c/c′=tanφ/tanφ′

(9)

本文用强度折减法求解[15-16]时，本构模型选用摩尔-库仑准则[17]，结合有限元方法判定边坡稳定性。

2 工程实例

2.1 工程概况

某排土场位于广东省惠州市，属地处亚热带季风气候，3～9月为雨季。年平均降雨量2 087.8 mm，最大降雨量为3 069.6 mm，最小降雨量为1 141.6 mm。根据当地气象局自1954年以来观测记录，当地日最大降雨量为275.2 mm(100年一遇)。

现场踏勘发现，该排土场介质主要为采矿过程中废弃的各种强风化土，排土场内的物料主要通过分层进行叠加堆放，底部主要堆放灰岩、砂岩、页岩等大颗粒的废渣，排土场台阶高度10 m，分层厚度约3 m，上部堆放第四系表土黄土层，如此循环，直到设计的高度，最终形成三级堆土台阶。由于边坡上部截排水沟设置不完善，边坡下缘存在多处滑移裂隙(图2)，若遇暴雨冲刷，容易发生局部坍塌失稳。

2.2 土力学试验

2.2.1 渗透性试验

试验分别测定矿山不同区域、不同土体的渗透系数(k)。主要仪器为WS-55型渗透仪(图3)，土样来源于露天采坑，制备成满足要求的饱和样本(图4)。共制备样本12个，其中Ⅰ-1、Ⅰ-2样本取自采坑顶板扰动土，Ⅰ-3、Ⅰ-4土样取自采坑底板扰动土，Ⅰ-5样本取自采坑底板原样土。Ⅰ-1样本2个，编号为Ⅰ-1-1、Ⅰ-1-2；Ⅰ-2样本2个，编号为Ⅰ-2-1、Ⅰ-2-2；Ⅰ-3样本2个，编号为Ⅰ-3-1、Ⅰ-3-2；Ⅰ-4样本3个，编号为Ⅰ-4-1、Ⅰ-4-2、Ⅰ-4-3；Ⅰ-5样本3个，编号为Ⅰ-5-1、Ⅰ-5-2、Ⅰ-5-3。

图4 部分渗透试验样本Fig.4 Partial penetration test samples

部分试验结果如表1。

表1 土体渗透试验结果表

2.2.2 三轴剪切试验

本次剪切试验(UU)采用的仪器为SJ-1A三轴剪力仪(图5)。试验样本为Ⅰ-1土样、Ⅰ-3土样、Ⅰ-5土样，其中Ⅰ-1样本4个，编号为4、6、10、12；Ⅰ-3样本5个，编号为1、5、9、11、13；Ⅰ-3样本4个，编号为2、3、7、8。每次采用3～4个圆柱形土样，将其分别置于不同的周围压力下，测试样本的抗剪强度参数，土体破坏准则为摩尔-库仑破坏准则。在施加周围压力和随后施加偏应力直至剪坏的整个试验过程中，样本不允许排水，加压直至土样剪坏(如图6)，可以测得应力抗剪强度指标c，φ。

图5 SJ-1A三轴剪力仪Fig.5 SJ-1A triaxial shear apparatus

图6 土样破坏实景图Fig.6 Real picture of soil sample failure

试验结果如表2所示。

3 算例分析

3.1 模型构建

1)数值模型

根据矿山排土场现状地形图和原始地形图建立典型剖面(图1)得到数值模型，如图7所示。

图7 数值模型剖面图Fig.7 Section of numerical model

2)参数选取

土层1取Ⅰ-1土样和Ⅰ-2土样的平均渗透系数，土层2取Ⅰ-3土样和Ⅰ-4土样的平均渗透系数，强风化岩取Ⅰ-5土样的平均渗透系数(表1)。土层1的强度参数取Ⅰ-1土样的平均强度参数，土层2的强度参数取Ⅰ-3土样的平均强度参数，强风化岩的强度参数取Ⅰ-5土样的平均强度参数(表2)。

表2 土体三轴剪切试验结果表

运用Midas进行有限元数值计算，采用Van Genuchten模型[18]拟合非饱和土的土-水特征曲线，其余参数如表3所示。

表3 各土层参数表

3)降雨工况设计

为详细探讨降雨强度与不同土层饱和渗透系数关系对分层边坡渗流过程的影响，本文设置了3种降雨工况，在总降雨时长为5 d时，考虑弱降雨、中降雨、强降雨3种降雨强度等级，强度大小分别为1×10-6、3×10-6、5×10-6m/s。其中强降雨工况的降雨强度大于土层1的饱和渗透系数，弱降雨工况的降雨强度小于土层2的饱和渗透系数，而中降雨强度介于这两者之间。

3.2 降雨条件下体积含水率θs分析

降雨初期，由于地表土体较干燥，降雨全部能渗入到土体内，随着降雨入渗的累积，边坡浅层部分逐渐饱和，且随着时间推移，湿润锋深度不断下移。为详细分析这种渗流变化特性，需要通过土体的体积含水率判定。图8为在3种降雨强度下随时间变化的瞬态体积含水率沿高程分布状态，可以看出：

1)弱降雨条件下，由于降雨强度小于各土层渗透系数，土层土体始终处于非饱和状态，随着降雨持续进行，体积含水率随高程呈线性减小。

2)中降雨条件下，在降雨3 d之前，土层1土体均处于非饱和状态，体积含水率随高程呈线性变化，3 d之后，土层1开始出现饱和层，由于此时降雨强度大于土层2的渗透系数，土体表面降雨补给速度小于入渗速度，湿润锋到达土层1与土层2交界面时，其入渗的速度由土层2的渗透系数决定，导致部分雨水不能及时入渗，交界面处土体的体积含水率迅速升高，土层1在4 d时再次出现非饱和层。

3)强降雨条件下，边坡浅层土体达到饱和状态所需要的时间更短，在降雨时间持续0～1 d时，坡积土层表面始终保持饱和状态不变，1～2 d之后，土层1出现饱和层，4～5 d之后，降雨开始入渗到强风化岩层，由于强风化岩层的渗透系数较小，浅层土体很快达到饱和状态。

图8 不同降雨强度下体积含水率分布Fig.8 Distribution of volume moisture content under different rainfall intensities

分析以上结果：当降雨强度均小于2种土层的饱和渗透系数时，相同时间内的总降雨入渗量较小，各层土体均未达到饱和状态；当降雨强度增大时，坡积土表面的雨水入渗速度大于补给速度，此时土体难以达到饱和；但随着降雨持续入渗，雨水补给速度能够大于入渗速度，导致中、强降雨比弱降雨时更快达到饱和状态；当降雨强度均大于2种土层的饱和渗透系数时，坡积土表面的降雨补给速度总是大于入渗速度，各个土层均可以得到有效降雨补给，迅速达到饱和状态。

3.3 降雨条件下边坡雨水入渗深度Hf分析

数值计算得到的3种降雨强度等级下雨水入渗深度时程曲线如图9所示。分析可知：边坡雨水入渗深度随着降雨持续而增加，降雨0～1 d时入渗深度的增幅(即入渗速度)最大，随后减小。究其原因，降雨1 d内，由于地表土体渗透系数较大，雨水全部入渗，饱和区在浅层形成的速度很快；强降雨条件下，降雨持续4～5 d时，降雨入渗经过土体分层界面到达土层2时曲线变得平缓，说明降水在强风化岩中的入渗速度非常缓慢。

图9 入渗深度与降雨时间关系变化曲线Fig.9 Variation curves of relationship between infiltration depth and rainfall time

图10为降雨强度为3×10-6m/s时，降雨入渗深度的理论与数值计算值的时程曲线图。此时，降雨强度小于土层1饱和渗透系数3.6×10-6m/s，根据式(2)计算不同时间的降雨入渗深度，利用式(1)得到雨水到达土层1与土层2分界面的时间4.8 d，此时雨水的入渗深度为3.6 m。当降雨到达土层1与土层2交界面后，降雨强度大于土层2的饱和渗透系数，利用式(8)计算不同时间点条件下雨水的入渗深度，利用式(7)计算得到雨水到达土层2与强风化岩交界面的时间为8 d，此时雨水的入渗深度为6.2 m，以此得到降雨入渗深度的理论计算结果。

图10 入渗深度的理论计算值与数值模拟值Fig.10 Theoretical calculation value and numerical simulation value of infiltration depth

通过3.1节的渗流模型可以得到数值计算的降雨入渗深度结果，并绘制成时程曲线。将上述理论计算值与数值计算值进行比较，可以发现在降雨初期，其雨水入渗深度的理论值与计算值出现偏差，但总体趋势基本吻合，雨水入渗深度的理论计算值小于数值计算值。出现这种误差可能是由于土层2的渗透性较小引起土层1中出现积水现象，因此出现随降雨时间不断变化的动水压力，导致雨水的入渗深度的理论值小于数值计算值。

3.4 降雨对分层边坡安全系数F的影响分析

数值计算得到的3种降雨强度下安全系数随降雨时间的变化曲线如图11所示。分析可知：3种降雨强度条件下，第1 d的安全系数相较自然状态均下降最明显，另外在中降雨4～5 d和强降雨2～3 d时，安全系数下降斜率也相对较大，这是由于湿润锋到达土层1、土层2分层界面时，降雨强度大于土层2的渗透系数，且随着降雨的持续进行，湿润锋上部土体含水率增加，土体重度增加，边坡土体的强度下降，进而稳定性降低。

图11 安全系数随降雨时间变化曲线Fig.11 Curves of safety factor with rainfall time

该矿实际降雨强度最大达到中降雨条件，根据《有色金属矿山排土场设计规范》(GB5021—2007)的规定，取允许安全系数[Fs]允=1.15，排土场边坡处于稳定状态。

4 工程验证

该矿山边坡监测系统采用GNSS实时在线监测位移系统，本文研究排土场监测点布设如图12，数据表明(图13)，2019年1～12月间，最大位移变形点为1#监测点，Z方向最大位移为32 mm；其余各点X/Y/Z方向位移变形幅值均在24 mm箱体空间振荡，处于合理变形范围内，表明该排土场边坡处于稳定状态，验证了计算结果正确性。

图12 排土场边坡位移监测实景Fig.12 Displacement monitoring of waste dump slope

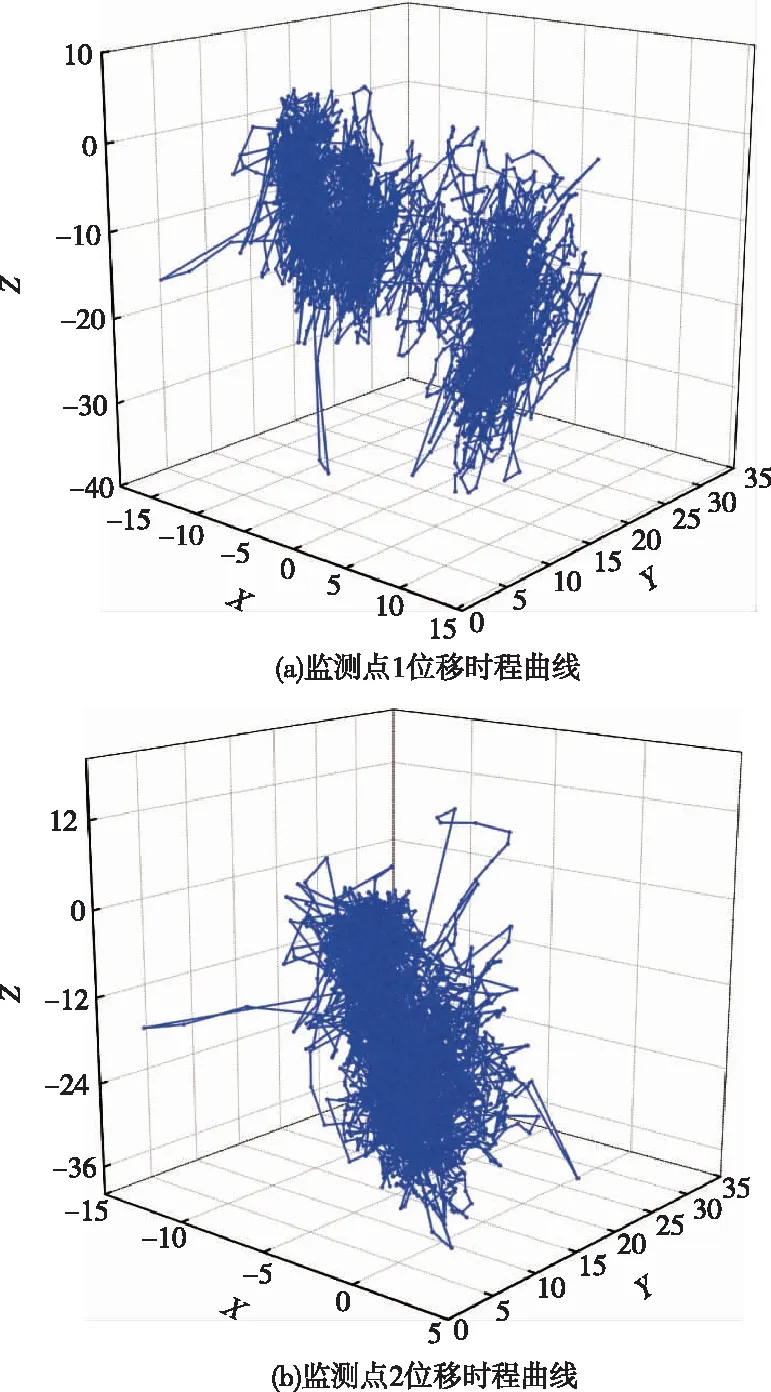
图13 排土场边坡位移监测时程曲线(单位：mm)Fig.13 Displacement monitoring time history curves of waste dump slope

5 结论

1)针对岭南沿海地区露天矿山排土场边坡分层特征，提出了一定降雨时间降雨强度下降雨入渗深度计算方法，实例分析表明，数值模拟结果与理论公式得到结果基本一致，该计算方法能够较好地反映分层结构土层边坡降雨入渗过程，为该类边坡在降雨条件下的入渗深度计算提供了方法支持。

2)降雨入渗过程中，当降雨强度大于土层的饱和渗透系数时，土层浅层很快达到饱和状态，降雨入渗速度由渗透系数控制；当降雨强度小于土层的饱和渗透系数时，土层表面体积含水率为等降雨强度体积含水率，且降雨入渗速度由降雨强度控制。

3)结合有限元方法计算边坡的安全系数，在降雨初期以及湿润锋到达土体分层界面时，安全系数降幅最大，随后安全系数降幅逐渐减小且趋于稳定，根据某矿山实际降雨情况，理论计算与工程实际均表明研究对象处于稳定状态，表明理论计算的合理性。