隐身飞机投弹对防空武器前置角误差的影响

刘明杰，王春阳，曾会勇，包磊，潘鑫锐，周长霖

(1.空军工程大学 a.研究生院；b.防空反导学院，陕西 西安 710051；2.国防科技大学 信息通信学院，湖北 武汉 430019)

0 引言

隐身飞机是当前世界各军事强国所依赖的重要空袭作战兵器，隐身飞机的隐身性能以及其给防空武器带来的影响已经成为国防工业部门研究的重点。

目前，隐身飞机降低雷达反射波强度主要是通过外形设计来实现，而战斗机在执行任务时要携带导弹等杀伤性武器，但外挂在飞机表面的导弹会严重破坏飞机的外形特征，导弹的弹体、弹翼可能与机体表面形成角反射体，导致雷达波的强烈反射。因此隐身飞机携带导弹多采用内埋式弹舱的载弹方式来保持其隐身性能。目前，研究隐身飞机的作战能力以及内埋式弹舱的成果较多，文献[1]主要介绍了内埋式弹舱在各类型飞机上的应用情况，并重点论述了F-22战机的内埋式武器弹舱的弹舱样式和舱内的武器发射系统；针对战斗机的投弹问题，文献[2-3]均对飞机的投弹过程进行了模型的建立，除此之外，文献[2]还研究了不同状态下的飞机投弹后的动态响应，文献[3]则是深入开展了无人机投弹过程仿真系统的设计开发、测试与评估工作；文献[4-5]重点研究了超声速条件下，不同马赫的飞行速度对机弾分离相容性的影响；文献[6]对导弹在弹舱内不同位置对机弹分离的影响进行了分析，并对超声速条件下多种不同情况弹舱内的流场进行了被动控制数值计算；在隐身飞机的实际突防作战能力方面，文献[7-8]研究了动态提取RCS(radar cross section)的隐身飞机隐身性能分析方法；文献[9-10]以文献[7-8]的RCS分析为基础,分析了不同战术干扰对雷达性能的影响；文献[11]则在文献[7-10]的基础上，对隐身飞机投弹对雷达检测性能的影响进行了研究。然而，雷达只是防空武器系统中的一部分，雷达所受到的影响最终都会通过火力控制系统转化到武器系统上并影响到武器的发射。因此，对隐身飞机作战影响防空武器发射的内在机理进行分析也十分重要，尤其是在研究隐身飞机突防投弹作战对防空武器发射的影响问题还存在着不足，相关研究成果也相对较少。

针对关于隐身飞机投弹对防空武器发射的影响分析不足的问题，本文综合文献[1-11]中内埋式弹舱载弹的投弹过程与隐身飞机突防航迹设计，对隐身飞机投弹过程对防空武器前置角误差大小的影响问题进行了研究，并对参数测量误差对防空武器发射前置角的影响机理展开了分析，深入研究了隐身飞机突防投弹对防空系统武器发射前置角的影响问题。

1 隐身飞机投弹模型

1.1 投弹航迹模型

隐身飞机内埋式弹舱载弹方式使隐身飞机投弹过程十分复杂，分析隐身飞机的投弹过程需结合飞机投弹的空气动力和空气流速的影响因素，充分考虑投弹时的弹舱开闭、弹体分离产生的干扰力矩等因素对机体稳定的影响。另外，飞机在投弹时经历了先俯冲送弹，弹体送出后快速爬升离开的姿态变化过程。

为对隐身飞机突防投弹作战对防空武器发射前置角的影响问题展开研究，建立如图1所示的隐身飞机投弹平飞航迹。本模型忽略了空气流速、干扰力矩等影响问题，简单模拟隐身飞机突防地面防空武器系统的封锁区并执行投弹任务的作战过程。

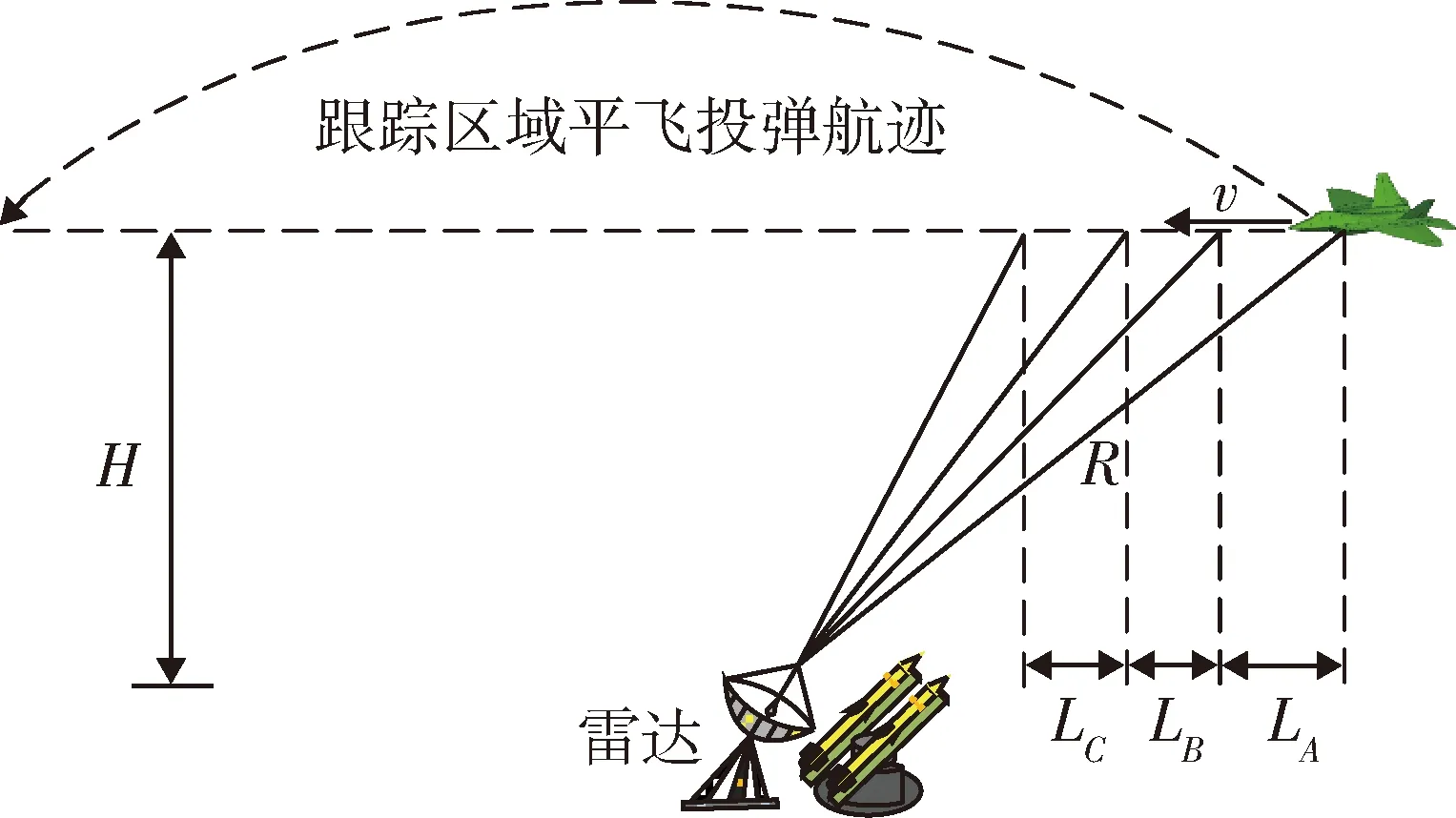
图1 隐身飞机投弹航迹模型Fig.1 Track model of the stealth aircraft bombing

图1中，R是雷达对某型隐身飞机的平均探测区域范围，其中隐身飞机以相对恒定的飞行速度v与高度H向站平飞并进行投弹，打击重要目标，完成作战任务。现将隐身飞机向站平飞突防投弹过程分为LA，LB，LC3个阶段，LA阶段为隐身飞机发现目标阶段，LB阶段为隐身飞机飞行并瞄准打击目标释放导弹阶段，LC阶段为隐身飞机投弹结束后迅速飞离阶段。

1.2 投弹过程RCS获取

隐身飞机的RCS是姿态角的敏感函数，而在隐身飞机动态飞行下，其姿态信息由机体在空间中的方位角、俯仰角、滚转角联合反映。因此，目前常用的获取隐身飞机动态RCS的方法是建立隐身飞机投弹静态RCS数据库，解算飞机飞行航迹下的即时方位、俯仰二维姿态信息，并利用插值计算的方式提取对应航迹下的RCS序列。

在构建隐身飞机投弹静态RCS数据库时，隐身飞机在弹舱开启状态的散射特性与机体的差异性会使整体机身产生较强的电磁散射，此时隐身飞机机体电磁散射特性会有猛烈的增高。因此为有效在实验平台模拟投弹过程，在原国外某型先进的隐身战机的同等比例缩小模型上增添弹舱，然后再导入电磁仿真计算软件，计算得出在弹舱开闭状态下的全方位静态RCS数据库。电磁仿真软件中条件设定为：极化方式：VV极化方式；工作频率：1 GHz;视线方位角：0°；视线俯仰角：-90°～90°；角度间隔：0.1°。

2 雷达测量误差模型及防空武器发射前置角误差模型

雷达测量误差是指测量值与真实值之差的均方根。在雷达对目标形成连续跟踪时，雷达对目标参数的测量误差将影响到火控系统计算武器发射的前置角，如果雷达对目标参数信息测量误差较大，则会引起防空武器发射前置角的较大预测误差，导致武器脱靶。

2.1 雷达测量误差模型

2.1.1 信噪比

雷达接收机内的噪声功率相对目标回波信号功率越大，雷达在估计目标回波信号参数信息时不稳定因素越大，因此雷达测量目标参数的精度与信号噪声功率比有关。对雷达方程进行变换，可得信噪比计算公式为

(1)

式中：Pt为雷达发射机峰值功率；Gt=Gr为收发一体天线的主瓣增益；σt为t时刻隐身飞机动态RCS值；λ为雷达工作波长；Rt为隐身飞机与雷达间的距离；k为玻尔兹曼常数；T0为内部噪声温度；Bn为接收机带宽；Fn为接收机的噪声系数；Ls为雷达各部分损耗引入的损失系数。

2.1.2 雷达测量误差模型

由于噪声的存在，雷达对目标状态参数的测量就是在随机性的噪声背景下对参数的估计。对于一般的雷达而言，只需要测量出目标的距离与角度信息便可以实现对目标的定位。目标距离信息的获取是通过估计信号的时间延迟来实现，角度信息的获取目前广泛采用的是单脉冲技术，但是因为噪声的存在，雷达对于目标距离与角度的估计不可能是完全准确的，均存在一定的测量误差。根据参数估计理论，对于目标参数的测量存在最大的测量精度，即最小的测量误差，这个最小的测量误差也被称为克拉美罗界[12-13]。

根据参数估计理论，目标距离的测量误差为

(2)

式中：ΔR为距离测量误差；c为电磁波传播速度；B为雷达信号带宽；S/N为雷达接收机内信噪比。

角度测量误差为

(3)

式中：Δθe为角度测量误差；τ为雷达信号脉冲宽度；fr为雷达信号脉冲重复频率；β为雷达天线伺服系统带宽。

2.2 防空武器发射前置角误差模型

2.2.1 距离测量误差和前置角误差

为方便分析距离跟踪误差对前置角误差的影响，假设雷达与防空武器发射架处于同一位置且除距离维测量误差外，其他目标参数无测量误差；距离维的测量误差引起的前置角误差原理示意图如图2所示。

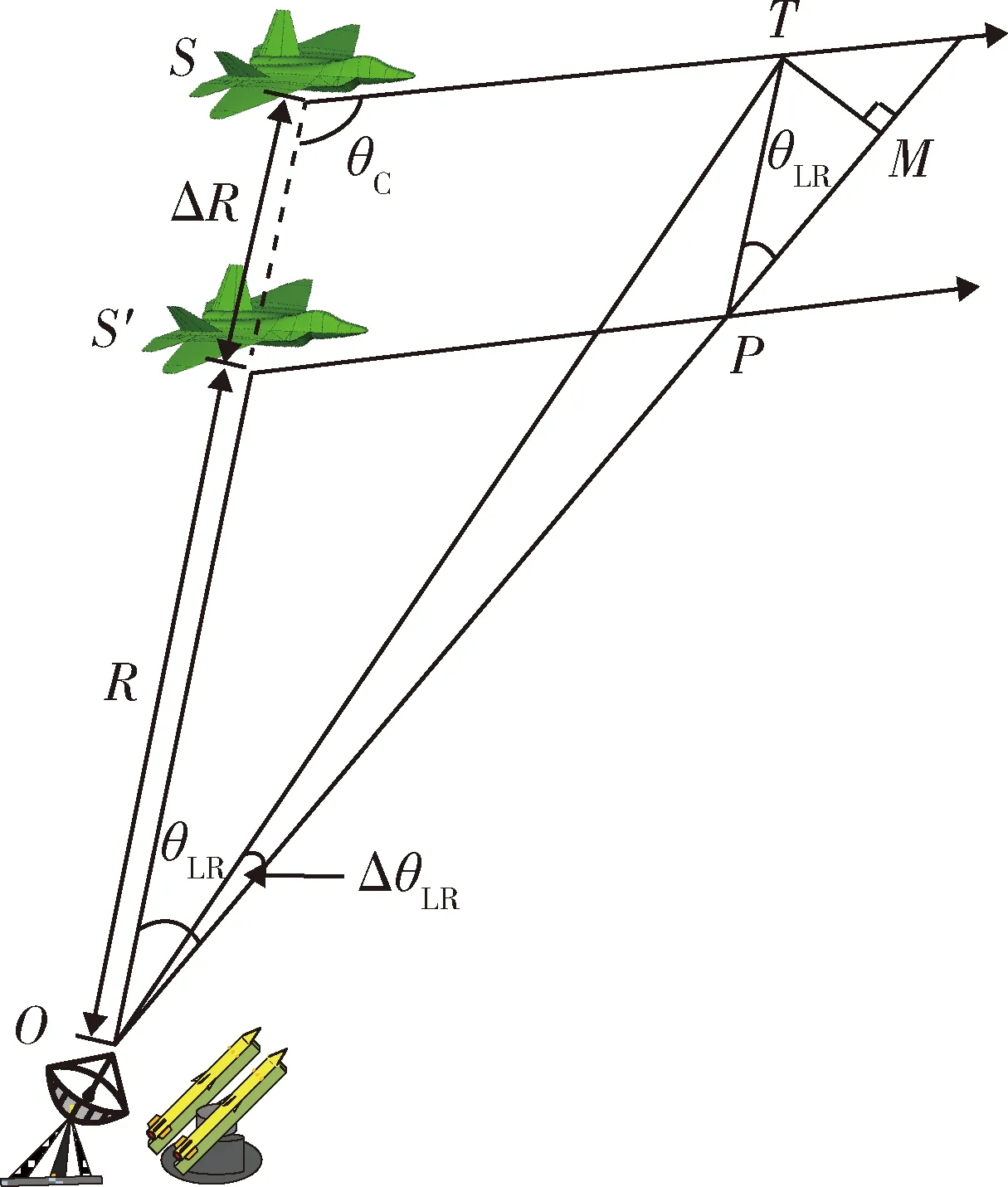
图2 距离测量误差引起前置角误差原理示意图Fig.2 Principle of lead angle error caused by distance measurement error schematic diagram

图2中，T为隐身飞机与防空武器的正确碰撞点；P为隐身飞机与防空武器的预测碰撞点；SO为隐身飞机与雷达的实际距离；R(S′O)为防空武器发射前瞬间雷达测量的目标距离；ΔR为雷达测量的距离误差；θC为雷达测量的目标飞行航向角；θLR为火控系统计算的武器发射预测前置角；ΔθLR为武器发射前置角误差。

由图2可得，目标飞机与拦截武器的碰撞条件为

(4)

式中：vt为隐身飞机飞行速度；vm为武器飞行速度。

则武器发射的预测前置角为

(5)

在ΔS′OP中，根据三角函数关系得武器由发射到预测碰撞点所需时间为

(6)

如果雷达能够测得隐身飞机的飞行速度与隐身飞机到防空武器系统的距离，就能够计算出预测前置角与武器的运行时间[14-15]。

根据图2所示几何关系和三角函数定理可得

(7)

TM=ΔRsinθLR,

(8)

(9)

式中：ST=vtt，为飞机在防空武器发射到预测碰撞点所飞行的距离。

对式(9)进行整理,可得距离测量误差引起的前置角误差为

(10)

如果距离跟踪误差很小，前置角误差也会很小，则式(10)近似得

(11)

2.2.2 角度测量误差和前置角误差

雷达对目标在角度维度的测量误差同样会影响防空武器系统火控设备计算武器发射的前置角，与距离维测量误差影响前置角的影响机理不同，角度维的测量误差将直接影响前置角误差。

假设雷达仅在方位维存在测量误差，将雷达与目标统一到防空武器系统坐标系中，角度测量误差引起的前置角误差原理如图3所示。

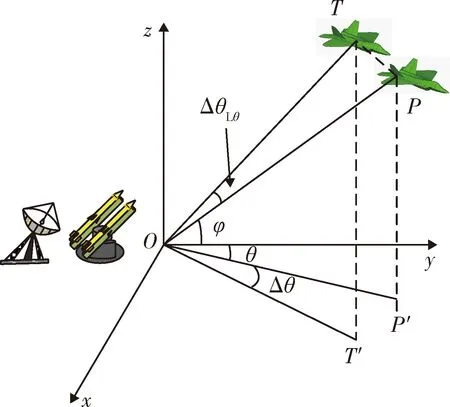
图3 角度测量误差引起前置角误差原理示意图Fig.3 Principle of lead angle error caused by angle measurement error schematic diagram

图3中,T为隐身飞机与防空武器的正确碰撞点；P为隐身飞机与防空武器的预测碰撞点；T′为隐身飞机与武器的正确碰撞点投影；P′为隐身飞机与武器的预测碰撞点投影；θ为武器发射前瞬间雷达测量的目标方位角；Δθ为武器发射前瞬间雷达测量的目标方位角误差；φ为武器发射前瞬间雷达测量的目标俯仰角；ΔθLθ为武器发射前置角误差。

根据图3所示几何关系得

cos ΔθLθ=cos2φcos Δθ+sin2φ.

(12)

由式(12)可得空间前置角误差为

ΔθLθ=arccos(cos2φcos Δθ+sin2φ).

(13)

2.2.3 总前置角误差与前置角误差评估模型

雷达在跟踪目标的多个参数时，每个目标参数都存在测量误差，这些参数测量误差均通过火控计算机处理后被转换到武器发射的总前置角误差。虽然机内噪声引起的参数测量误差均服从高斯分布，但总前置角误差不是服从高斯分布。而计算联合概率密度函数较困难，又因为在雷达跟踪目标的过程中，只要有一个维度的误差超过跟踪误差的最大限度，武器就会脱靶，所以本文在分析总前置角误差时用较大者近似为总的前置角误差[16],即：

ΔθL=max{ΔθLR,ΔθLθ}.

(14)

为有效衡量前置角误差对武器的影响，依据导弹的脱靶距离评价指标r与隐身飞机与雷达之间的距离R，近似得出武器发射前置角误差影响武器系统的有效性评价指标θst，具体为

(15)

因此，判断武器发射前置角误差对武器系统是否有影响的判决准则为

3 仿真分析

为突显隐身飞机投弹对防空武器系统的影响，将隐身飞机投弹航迹与非投弹航迹(正常航迹)对雷达及防空武器发射的影响进行对比分析。

3.1 隐身飞机投弹RCS序列

研究隐身飞机在飞行过程中的动态RCS需获取隐身飞机的姿态信息变化，计算隐身飞机相对雷达视线的方位角与俯仰角。结合目前X型隐身飞机超声速巡航速度与飞行时的投弹时间，对隐身飞机的飞行状态参数与投弹各阶段的时间进行设置，如表1所示。

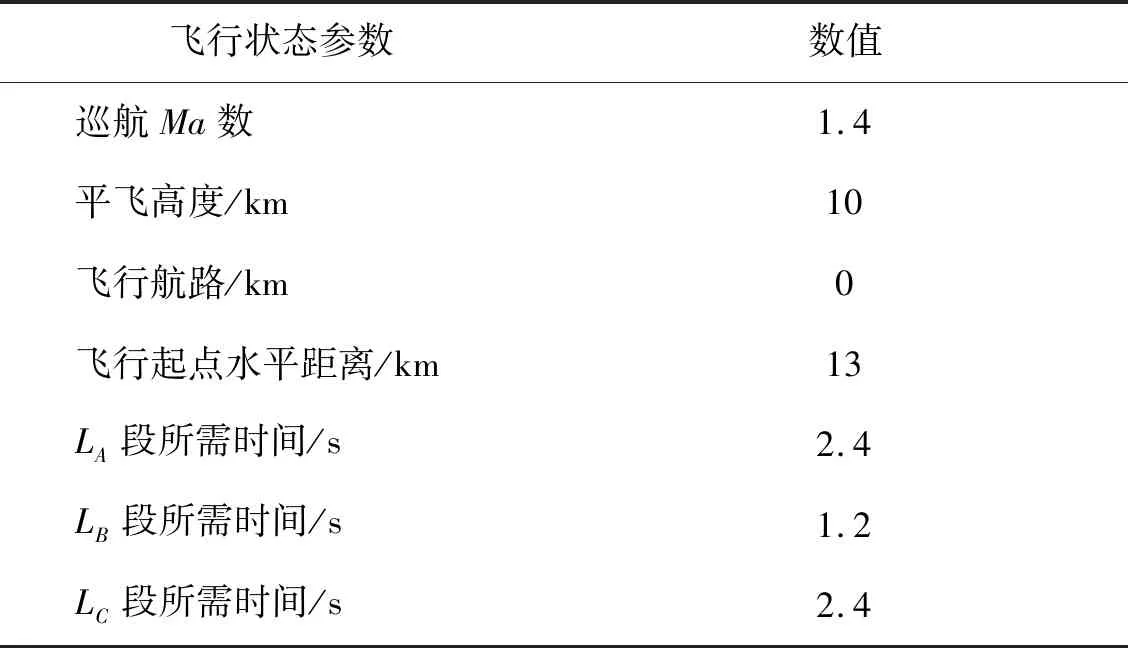
表1 飞行状态参数设置Table 1 Flight status parameters setting

通过飞行状态参数与飞行时间设置对姿态角度进行求解，求解结果为：视线方位角为0°，视线俯仰角范围为50.28°～61.40°。

在获得隐身飞机姿态角度后，对隐身飞机RCS进行仿真分析，以0.1 s为采样间隔对隐身飞机飞行过程进行采样，通过隐身飞机飞行过程中的方位角与俯仰角序列和隐身飞机RCS数据库进行RCS序列求解。具体情况如图4所示。

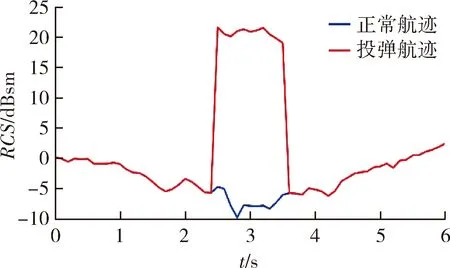
图4 RCS序列Fig.4 RCS sequence

从图4中可以看出，隐身飞机在正常航迹下的RCS变化范围为-9.690 0～2.518 1 dBsm，在投弹航迹下RCS变化范围为-6.133 2～21.610 5 dBsm。其中正常航迹与投弹航迹仅在2.4～3.6 s阶段(航迹中的LB段，也就是弹舱开闭过程)，隐身飞机的RCS有明显的不同，投弹航迹在此阶段的RCS相对正常航迹增加25～30 dBsm左右。表明在隐身飞机投弹飞行的过程中，飞机的微小姿态变化会导致RCS出现强弱上的差异。同时，在隐身飞机弹舱开闭的瞬间会引起较强的电磁散射，导致RCS急剧上升。

3.2 信噪比

根据求解信噪比的计算式，结合仿真得到的隐身飞机投弹航迹与正常航迹下的动态RCS序列与目前常规体制雷达设备的相关参数，对隐身飞机2种飞行状态下的信噪比进行仿真求解。

常规体制雷达参数设置见表2。

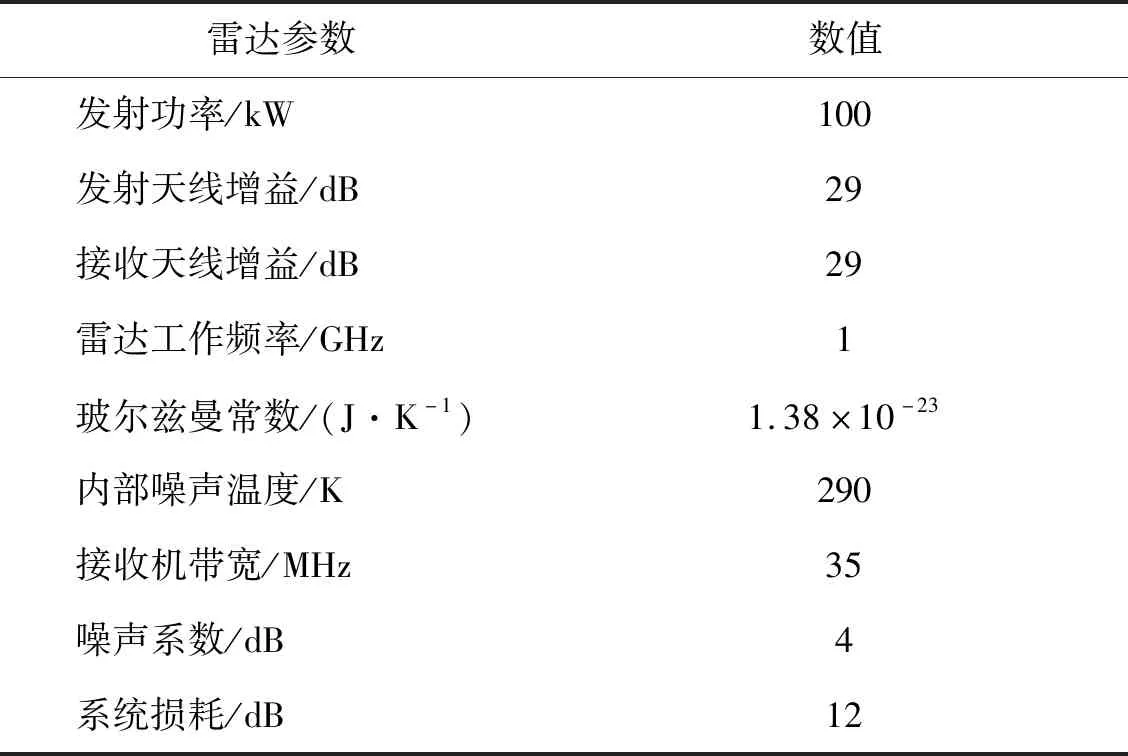
表2 雷达参数设置Table 2 Radar parameters setting

隐身飞机在2种不同飞行状态下的信噪比序列仿真结果如图5所示。

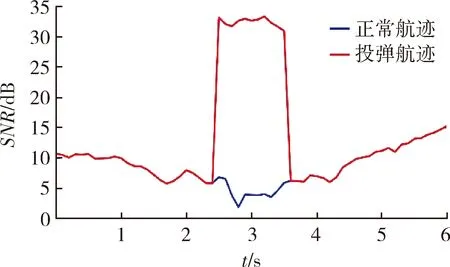
图5 信噪比Fig.5 SNR

从图5中可以看出，隐身飞机在正常航迹下的回波信号进入雷达接收机后的机内信噪比变化范围为1.970 3～15.361 3 dB，投弹航迹下的机内信噪比变化范围为5.837 4～33.342 8 dB，同时因为隐身飞机在弹舱开闭的过程中会使飞机的RCS急剧增加，因此在投弹阶段接收机内的信噪比得到了较大改善，改善程度达到了25～30 dB左右。

3.3 雷达测量误差

根据仿真得到的隐身飞机正常航迹与投弹航迹下的接收机内信噪比与参数测量误差模型，仿真求解隐身飞机在2种不同飞行状态下的距离与角度测量误差，仿真情况如图6所示。

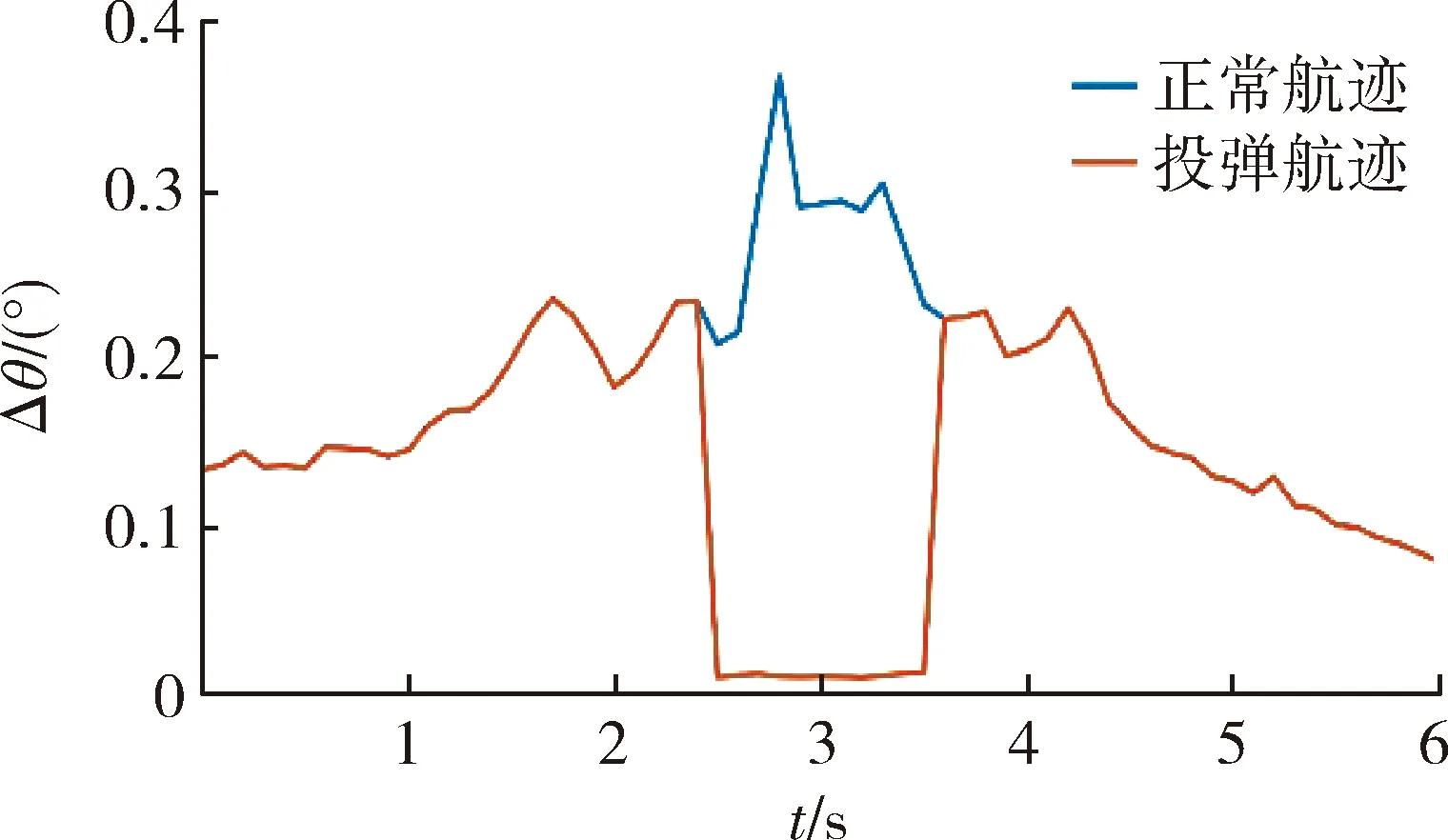
图6 角度测量误差Fig.6 Angle measurement error

由图6可知，在隐身飞机正常平飞航迹下，雷达对目标角度的测量误差在0.078 7°～0.367 8°范围内变化；在投弹航迹下，雷达对目标角度的测量误差在0.009 9°～0.235 7°范围内变化。且从图中可以看出，在投弹航迹下，因为弹舱开闭的投弹阶段使回波信号进入接收机内的信噪比得到了较好改善，所以雷达的角度测量误差在此阶段也得到了较大的提升，提升约0.38°左右。

同理，对雷达的距离测量误差进行仿真计算，结果如图7所示。

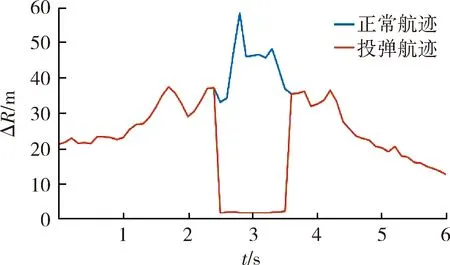
图7 距离测量精度Fig.7 Distance measurement accuracy

由图7可知，在隐身飞机正常平飞航迹下，雷达对目标距离的测量误差在12.46～58.26 m内变化；在投弹航迹下，雷达对目标距离的测量误差在1.57～37.32 m范围内变化。且从图中可以看出，在投弹航迹下，同样因为信噪比的改善，雷达的距离测量误差在此阶段也得到了较大的提升，提升约55 m 左右。

3.4 防空武器发射前置角误差

根据防空武器发射前置角误差模型与仿真计算出的雷达对目标参数的测量误差,仿真求解正常航迹和投弹航迹下的距离维误差和角度维误差分别引起的武器发射前置角误差，仿真结果如图8所示。

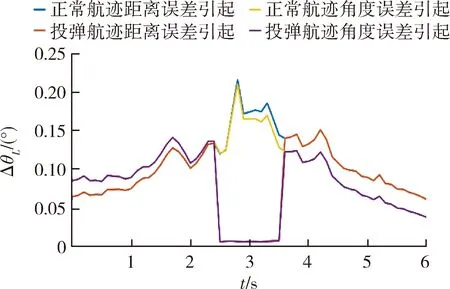
图8 防空武器发射前置角误差Fig.8 Lead angle error of weapon launch

由图8可知，在隐身飞机正常飞行航迹下，防空武器系统因雷达对目标距离的测量误差引起的武器发射前置角误差在0.060 8°～0.216 2°范围内变化，因雷达对目标角度的测量误差引起的武器发射前置角误差在0.037 7°～0.210 4°；在投弹航迹下，防空武器系统因雷达对目标距离的测量误差引起的武器发射前置角误差在0.005 9°～0.151 4°范围内变化，因雷达对目标角度的测量误差引起的武器发射前置角误差在0.005 6°～0.141 4°范围内变化。由图中仿真曲线可以看出，因为弹舱开闭期间的电磁反射增强导致目标参数测量误差的减小使防空武器发射的前置角误差也减小了。

根据防空武器发射总前置角误差模型取距离误差和角度误差所引起的前置角误差中的最大值作为武器系统的总前置角误差。再根据前置角误差评估模型判断得出总前置误差是否能够影响武器系统的工作性能。

总前置角误差如图9所示。

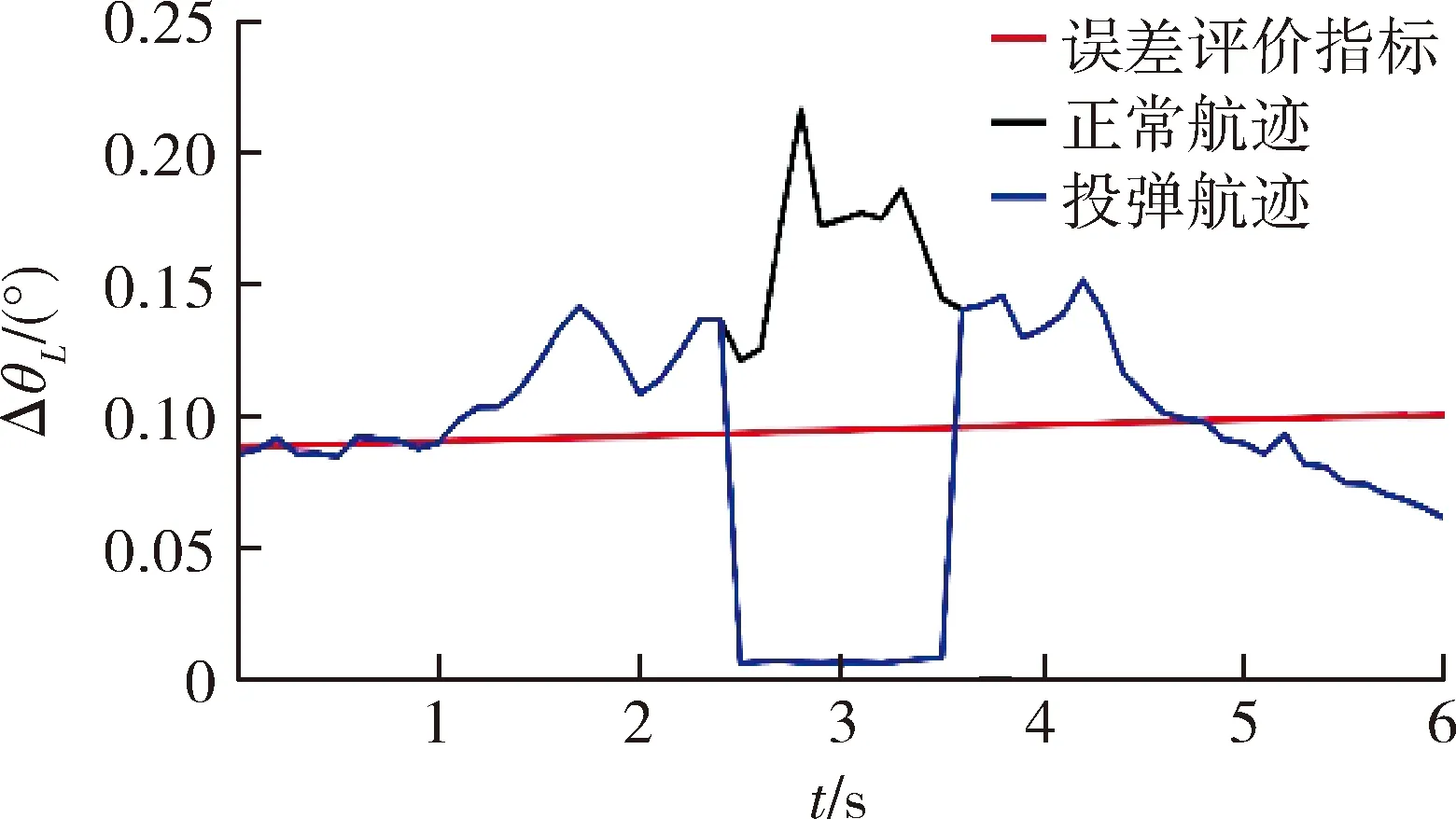
图9 防空武器发射总前置角误差Fig.9 Total lead angle error of air defense weapon launch

由图9可知，在隐身飞机正常平飞航迹下，因雷达对目标距离和角度的测量误差所引起的防空武器发射前置角总误差在0.060 8°～0.216 2°范围内变化；在投弹航迹下，防空武器发射前置角总误差在0.005 9°～0.141 4°范围内变化。

根据前置角误差影响判决准则可知，在雷达跟踪隐身飞机正常飞行航迹的情况下，雷达对目标角度与距离的跟踪误差所引起的前置角误差在0～1 s左右处于受影响边缘，4.6～6 s不受影响，其余时间武器发射均受到较大影响；雷达跟踪隐身飞机投弹航迹的情况下，由于在隐身飞机弹舱开闭的投弹期间会使回波信号大幅度增强，此时距离跟踪误差与角度跟踪误差所引起的前置角误差较小，系统在此期间控制防空武器发射能够更加精确地预测瞄准目标。

4 结束语

本文研究了隐身飞机投弹对防空武器发射前置角误差的影响问题。首先利用飞机的飞行姿态和隐身飞机RCS数据库确定平飞投弹航迹与平飞正常航迹下的动态RCS序列，依据雷达对目标的参数测量误差模型和武器发射前置角误差模型对武器发射的总前置角误差进行仿真求解，并根据前置角误差影响评价准则对隐身飞机投弹对防空系统的武器发射的影响进行判决分析。仿真结果表明：隐身飞机在弹舱开闭期间会增强自身对回波信号的反射，进而导致雷达接收机内的信噪比增大，使雷达对隐身飞机状态参数的测量误差减小，从而使得火控系统能够更加精确地预测武器发射前置角，准确瞄准空中目标，为武器的精确拦截打下基础。