基于特征提取和长短期记忆神经网络的铣刀磨损量预测

周成鹏，王卫军，侯至丞，冯 伟

（1. 中国科学院 深圳先进技术研究院，广东 深圳 518055；2. 中国科学院大学，北京 100049）

0 引言

铣刀作为高速数控机床的关键部件之一，在加工过程中，其磨损会严重影响工件表面的光洁度和尺寸精度。工业统计数据显示，刀具故障损坏是导致机床故障的主要因素，其产生的停机时间占据数控机床总停机时间的较大比例。当刀具在出现磨损故障但未被发现的状态下继续加工时，会导致刀具损坏、工件报废，甚至损坏机床。文献[1]通过对数百台加工中心的机床进行统计分析发现，每天有40～50把刀具损坏，其中大部分是由于刀具超过了使用寿命而造成的。准确可靠的刀具磨损量预测可有效指导生产，降低非必要的停机时间，节省制造成本，提高生产效率。工业4.0时代[2]的到来，使得工业大数据分析与应用成为重要的研究课题[3]，其中时间序列数据能够很好地反映工业进程中的关键变化，从而以此为依据进行故障预测。刀具磨损量预测就是基于工业采集信号数据来推断未来的磨损情况，了解加工过程的趋势，从而科学合理地评估刀具磨损的当前状态，实现生产过程质量的改善。

目前，评估刀具磨损状态可以使用直接监测和间接监测的方法。直接监测方法精度高,但需要停机测量而不能实现在线监测[4]。间接监测则是通过传感器来获取与刀具当前磨损状态有间接相关性的各种信号数据来实现的，适用于数字化智能制造系统。传感器主要用于采集工业过程中的三向力信号、高频振动信号、声发射信号和电流信号等。该方法通过对数据进行预处理和特征提取后，使用深度学习模型对刀具磨损量进行监测。

深度学习模型可以更好地适应时间序列数据中复杂的非线性关系。在非线性建模方法中，深度学习模型具有自适应、自组织学习机制，对非线性时间序列数据具有良好的预测能力。文献[5]提出基于支持向量回归(support vector regression, SVR)的刀具磨损量预测模型，其实验结果表明，该方法具有一定有效性。文献[6]针对数控铣刀的磨损问题，提出了决策树回归(decision tree regression, DTR)和集成方法AdaBoost相结合的刀具磨损量预测方法。文献[7]提出了一种基于分布式卷积神经网络的刀具磨损评估方法，对刀具磨损量进行预测。循环神经网络(recurrent neural network, RNN) 是时间序列预测模型中常用的工具[8]，模型特点是具有记忆空间，可对前置计算过程的结果进行存储。与传统神经网络中计算结果之间并没有相关性不同，RNN隐含层计算既采纳了当前的输入信息，也包含隐含层最后的计算过程状态。然而，RNN网络对于时间序列数据中的长距离依赖关系学习的能力较差，因为其只具备短期的记忆能力，当时间序列的长度过长时，容易造成梯度消失和梯度爆炸，因此出现了长短期记忆神经网络(long short-term memory, LSTM)、门控循环单元(gate recurrent unit,GRU)、简单循环单元(simple recurrent unit, SRU)等一些变体来解决这个问题。

因此，本文提出一种基于特征提取(feature extraction，FE)及LSTM的铣刀磨损量预测方法，即FE-LSTM。该方法通过建立时域、频域和时频域分析，提取原始信号数据对应特征；LSTM可充分利用工业数据的时间序列特性，自适应地学习所提取特征之间的复杂隐含关系，并具备长距离依赖学习能力，可避免出现梯度爆炸和梯度消失问题，从而精准地预测铣刀的磨损量。

1 铣刀磨损量预测模型

采用间接监测方法，通过对传感器所采集的工业原始信号数据进行数据分析及特征提取，结合长短期记忆神经网络建立铣刀磨损量预测模型。

1.1 长短期记忆神经网络

本文所提方法基于特征提取及长短期记忆神经网络来预测铣刀的磨损量，其主要框架如图1所示。

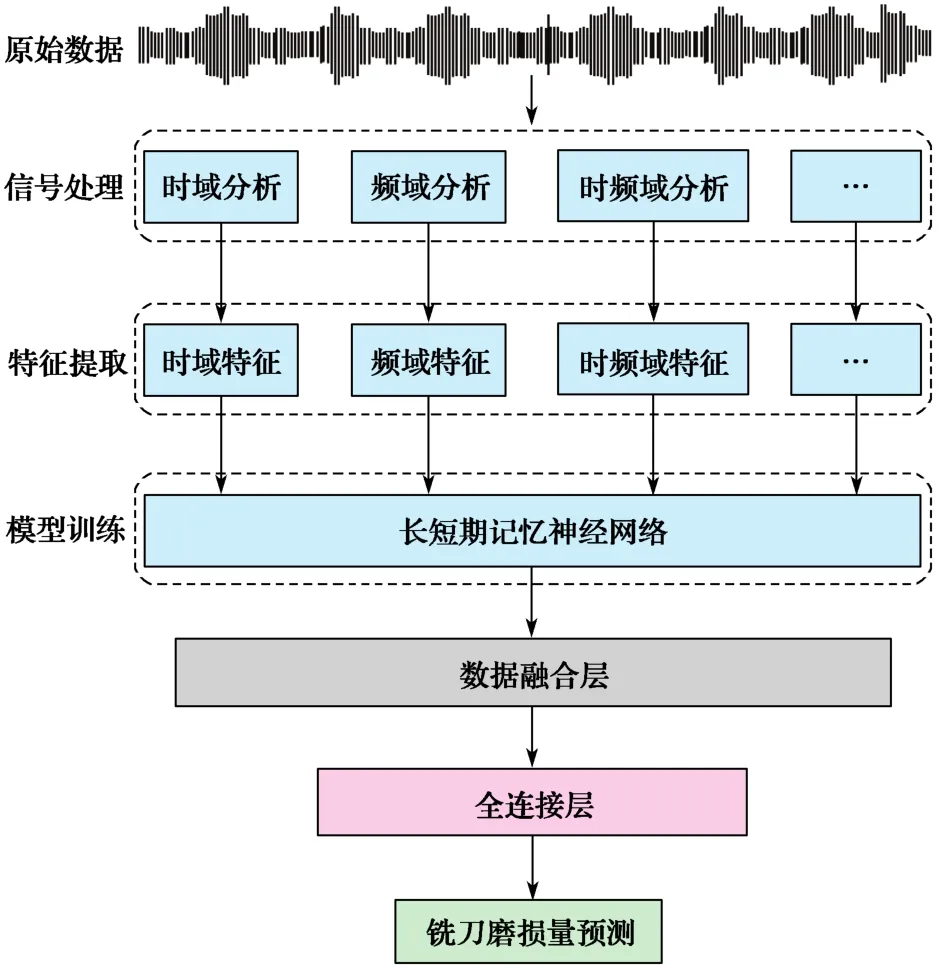
图1 铣刀磨损量预测模型Fig. 1 Wear prediction model of milling cutter

LSTM是循环神经网络RNN的变体。RNN算法适用于处理序列问题，属于全连接神经网络，主要是通过t时刻的输入Xt来计算得到隐含层输出ht。ht将会是（t+1）时刻RNN输入的一部分，因此RNN可以展开为图2右边的形式。

图2 RNN结构图Fig. 2 RNN architecture diagram

作为一种先进的RNN变体，LSTM可以自适应地捕捉时间序列数据中存在的长距离依赖和非线性动态变化[9]。LSTM与RNN的整体结构基本相似，不同之处在于每个隐含层内的计算方式。LSTM在隐含层计算中新增了细胞状态和门机制。LSTM的核心是细胞状态，RNN中的每个隐藏单元，在LSTM中变成了一个个有记忆功能的细胞；然后通过“门”机制来控制信息的记忆。LSTM中有遗忘门、输入门和输出门这3种控制门。遗忘门负责调节上一时刻细胞状态Ct-1可传递到当前时刻细胞状态Ct的比例，因此可保存长距离序列信息。输入门则负责调节当前时刻网络的输入Xt传递到Ct的比例，可以避免当前无关信息进入记忆。输出门决定Ct能够输出到LSTM的当前输出值ht的比例，进而控制长期记忆对当前输出的影响。控制门主要由点乘运算和sigmoid函数来实现。点乘运算决定了可以传输多少信息。sigmoid函数值范围在0到1之间：为0时，不会传输任何信息；为1时，传输所有信息。LSTM隐含层内的计算结构如图3所示。

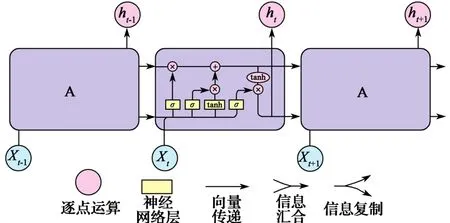
图3 LSTM隐含层计算结构Fig. 3 Calculation structure of LSTM hidden layer

使用上述细胞状态和控制门两种结构即可以实现对序列较早期信息的存储，充分掌握序列信息中的长距离相关性。利用细胞状态可以完成存储训练梯度的任务，从而避免发生梯度消失。在t时刻，LSTM的输入包括当前t时刻网络的输入值Xt、上一时刻LSTM的输出值ht-1以及上一时刻的细胞状态Ct-1。

1.2 构建铣刀磨损量预测模型

FE-LSTM铣刀磨损量预测模型由输入层、隐含层、全连接层和输出层构成，主要功能是在采集的信号样本数据和铣刀磨损量之间建立非线性映射关系。本文设计了一个输入特征维度为6、隐含层数为4、每层包含64个神经元的LSTM模型。输入层接收各传感器所采集的振动信号和切削力信号的敏感特征值；隐含层利用神经元进行特征提取；全连接层将LSTM学习到的特征映射到输出值，即铣刀磨损量。使用Dropout优化方式[10]防止过拟合，选取线性整流函数（rectified linear unit, ReLU）用于加强神经网络各层之间的非线性关系，防止梯度消失。LSTM网络在训练时会使用上一时刻的信息加上本时刻的输入信息来共同训练，在时间轴上传递隐含层状态。模型结构如图4所示。

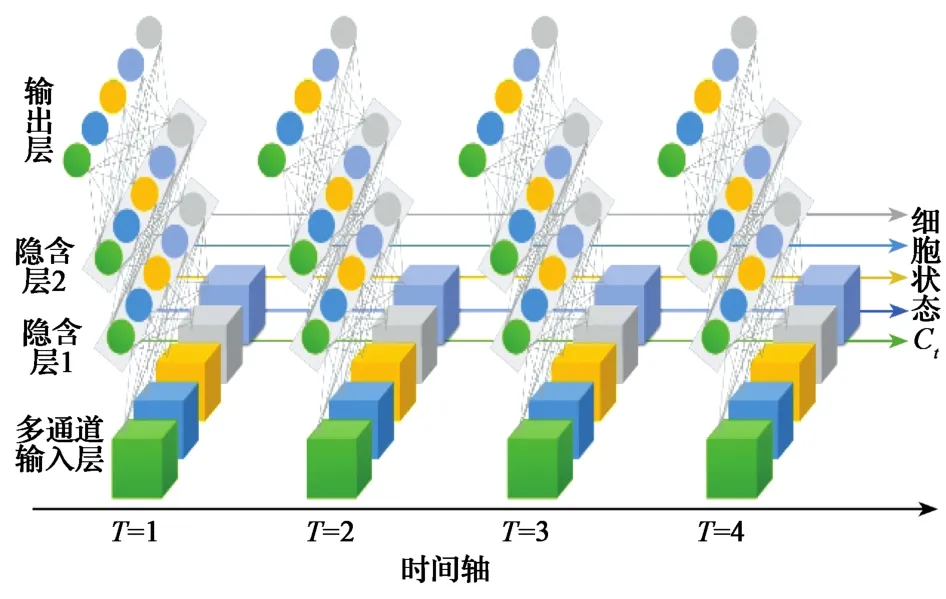
图4 FE-LSTM铣刀磨损量预测模型结构Fig. 4 Structure of FE-LSTM based prediction model for milling cutter

在FE-LSTM铣刀磨损量预测模型的训练阶段，选用Adam优化器来负责反向传播预测值与标签值之间的误差信息、优化隐含层内神经元的权值，使下一轮的预测值可不断逼近标签值。在该阶段，采用平均绝对误差(mean square error, MSE)来比较评价模型的性能：

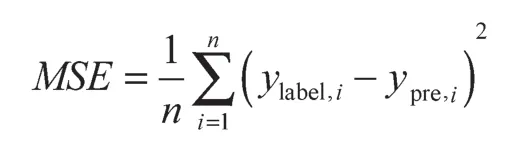
式中：ylabel,i——第i次走刀后铣刀磨损量的具体标签值；ypre,i——模型对于第i次走刀后铣刀磨损量的具体预测值；n——总走刀数。

2 特征工程

模型建立后，需通过实际铣刀加工数据进行模型训练及验证。通过分析实验数据集，进行特征工程，建立时域、频域及时频域分析，提取原始信号数据的有效信息，使预测方法达到更高精度。

2.1 实验数据集

本次实验选取的工业数据集是2010年故障预测与健康管理协会数据竞赛中的铣削刀具磨损量预测数据集[11]。该实验以3齿球头硬质合金铣刀作为研究对象，采用罗德斯 RFM760型高速数控机床作为实验平台，配合奇石乐9265B型三向测力仪和5019A型多通道电荷放大器以及NI-DAQ数据采集卡来采集加工过程中所产生的信号数据。

具体实验是将6把完全相同的3齿球头硬质合金铣刀在铣床上进行铣削实验，加工参数一致。铣刀每次走刀的长度为108 mm，选用徕卡MZ12型显微镜来测量铣刀每一次走刀结束后3个切削刃的后刀面磨损量，并记录相应的高频切削力信号、高频振动信号以及高频声发射信号。铣削主轴转速为10 400 r/min，进给速度为1 555 mm/min，轴向铣削深度为0.2 mm，径向铣削宽度为0.125 mm，每次走刀进给量为0.001 mm，采样频率为50 kHz。实验装置[12]如图5所示。

图5 实验装置Fig. 5 Experimental equipments

实验产生6份数据集（c1～c6），每份数据集对应315次铣削过程，其中c1，c4和c6是训练集数据，c2，c3和c5是测试集数据。每次铣削过程所采集的信号数据包括3个轴向的高频铣削力和振动信号，以及铣削过程中高频声发射信号的方均根值，总共有7个通道的数据，对应127 399～252 492条信号数据。每次铣削过程分别对应3个槽向（flute1，flute2和flute3）的磨损值，仅训练集c1，c4和c6有相对应的真实磨损值。

2.2 特征提取

综上所述，每次铣削过程对应数万条信号数据和一个真实的磨损值，但并非所有信号数据都与磨损量有关系，且原始信号中还夹杂着干扰噪声。实施适当的特征工程，筛选出对铣刀磨损量敏感的特征，不仅可以减小特征空间，加快模型训练速度，还可以有效提升模型的拟合效果。文献[6]采用互信息(mutual information, MI)评估方法和F-test检验方法进行了特征评估和选择，论证了声发射信号并未贡献出最优特征，故舍弃声发射信号数据。

对于每个独立样本(c1、c4和c6)的x轴、y轴、z轴铣削力和振动共计6个通道的信号数据进行独立分析处理，提取其时域特征、频域特征和时频域特征。

2.2.1 时域特征提取

有量纲特征值是对通道信号数据的时域描述。所选择的有量纲特征值包括绝对均值、峰值、均方根值、方根幅值、歪度值、峭度值、波形因子和脉冲因子等。所提取时域敏感统计特征可在一定程度上表征铣刀的不同磨损状况。图6示出x轴铣削力信号所提取的时域特征与走刀数之间的关系。

2.2.2 频域特征提取

将信号数据从时域转换到频域可通过数学处理方法来实现。 如傅里叶变换可将时域上连续或离散的信号数据变换成频域上的信号数据，使我们可以更清晰直观地在频域维度上去分析信号数据的频谱组成细节。本文采用快速傅里叶变换(fast Fourier transform, FFT)对铣削力和振动信号进行时频变换分析，提取重心频率、均方频率、均方根频率和频率方差等频域特征。

2.2.3 时频域特征提取

铣刀运行过程信号数据具有非平稳或准平稳的特点，使用时频域分析方法可以准确表征加工过程信号数据的特性。时频域分析常用的方法有小波变换(wavelet transform, WT)[13-14]和经验模态分解(empirical mode decomposition, EMD)。与EMD相比，小波变换具有坚实的理论基础[15]。小波包分解是比小波变换更为精细的分析方法，小波包分解对信号数据的全频带进行了多层次分解，可分离信号数据中与铣刀磨损量相关的各频带能量，而每个频带中相对能量的变化反映了铣刀的磨损量变化情况。故此处采用小波包分解来提取铣削力和振动信号的时频域特征。

对铣削力和振动信号进行3层小波变换分解，将信号拆分成8个不同频段，各个频段的特征即为其能量值。图7示出x轴铣削力信号所提取的时频域特征与走刀数之间的关系，可见随着走刀数的增加，铣削力信号所对应的各频段能量值呈现大致相同的走势，铣刀在加工过程中的磨损程度与铣刀力信号之间存在相关性。

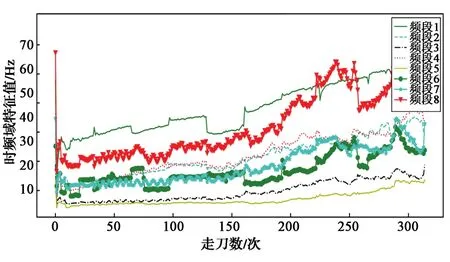
图7 时频域特征Fig. 7 Time-frequency domain features

最终，针对每一通道信号对应提取了24个特征。数据集c1, c4和c6各对应一组大小为315×6×24的特征空间，选定每次走刀过程结束后铣刀3个切削刃的后刀面磨损量的最大值作为标签值。

3 实验验证

通过分析实验数据以及进行特征工程后，提取了原始信号数据中的有效信息。为检验 FE-LSTM铣刀磨损量预测模型的有效性，需通过建立对比实验来多方面验证模型的预测准确性、适用性以及泛化能力等，并根据实验结果来对模型的性能进行评价。

3.1 实验设计

经过特征工程后，初始数据集相关信号数据被转换为对应大小的特征空间，将其作为模型的输入，配合所选定标签值对模型进行训练。训练过程中，计算采用平均绝对误差(MSE)作为损失函数，利用Adam优化器[16]使MSE最小。Adam优化器不同于传统的随机梯度下降(stochastic gradient descent, SGD)，SGD没有动量和自适应学习率的概念，收敛速度慢且可能在鞍点处振荡。Adam优化器可以自适应调节参数的学习率，从而大幅提升训练速度，提高稳定性，使模型预测值不断接近标签值。此外引入Dropout算法对模型进行正则化，防止过拟合。Dropout在模型训练过程中会根据所设定的参数随机屏蔽部分神经元，从而形成新的网络结构，且神经元之间彼此互不依赖，可减少神经网络模型在特征学习过程中的局部性特征依赖，从而进一步提升神经网络的稳健性。最后将未经训练过的测试数据集输入到训练完成后的FE-LSTM模型中，从而实现有效的铣刀磨损量预测。实验框架如图8所示。

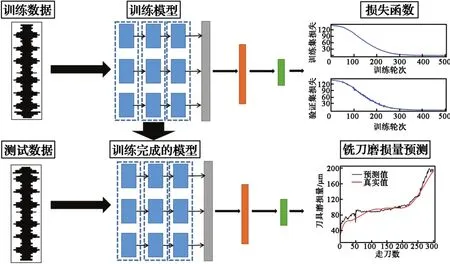
图8 实验框架Fig. 8 Experimental framework

为检验FE-LSTM模型对铣刀磨损量预测的有效性，实施3个不同的对比实验。

实验一：探究不同隐含层数对FE-LSTM预测性能的影响。隐含层数集合为{2, 4, 6, 8}，采用MSE作为FE-LSTM预测性能的评价指标。

实验二：选用“留一组”交叉验证实验分析方法，验证FE-LSTM铣刀磨损量预测方法对未知的一组数据集的预测准确性和适用性，从而可有效检验模型的泛化能力。在训练过程中，按8∶2的比例随机划分c1和c6样本数据作为训练集和验证集。记录各训练轮次中训练集和验证集上的损失值。训练500轮后完成模型训练，而后输入c4样本数据作为测试集进行测试实验。

实验三：将FE-LSTM模型与不同模型进行性能对比，如SVR模型[17]、卷积神经网络(convolutional neural network, CNN)[18]与反向传播神经网络(back propagation neural network, BPNN)[12]，采用平均绝对误差(MSE)和平均绝对误差百分比(mean absolute percentage error, MAPE) 这两项指标来比较模型的性能。MAPE计算公式为

3.2 实验结果分析

表1示出模型不同隐含层个数对应的平均绝对误差大小。可以看出，对于FE-LSTM铣刀磨损量预测模型，隐含层个数为4时性能最佳。因而实验二和实验三均设定模型隐含层个数为4。

表1 不同隐含层个数实验结果Tab. 1 Experimental results of different hidden layer numbers

表2示出训练过程中对应轮次的训练集损失及验证集损失具体数值，图9示出对应的损失函数变化曲线。图中，x轴是FE-LSTM模型的训练轮次，即模型在训练阶段内部权重参数更新迭代的次数；y轴是训练集以及验证集上损失函数的值。可见，随着训练轮数的增多，损失函数的值不断减小直至收敛（趋近于零），即铣刀磨损量预测值与实际测量值之间的误差MSE不断减小并最终收敛，说明模型较好地学习了所提取的信号数据特征。此外，训练集与验证集对应的损失函数均成功收敛，并且在两个数据集上损失函数最终收敛的值相差无几，表明FE-LSTM铣刀磨损量预测模型具有良好的泛化能力。

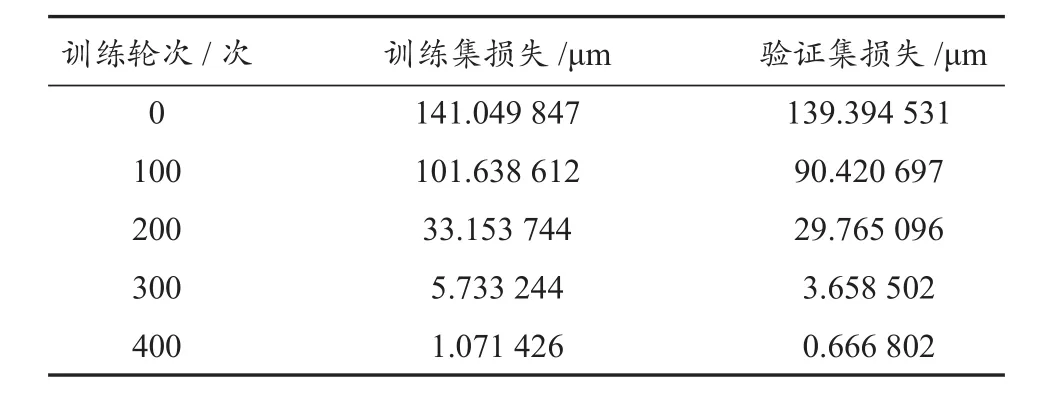
表2 训练过程实验结果Tab. 2 Experimental results of the training process

图9 损失函数变化曲线Fig. 9 Loss function curve

图10示出铣刀磨损量预测值和测试值的变化曲线。可以看出，模型预测值与真实值的变化趋势一致，证明了FE-LSTM模型能有效适用于铣刀磨损量预测。

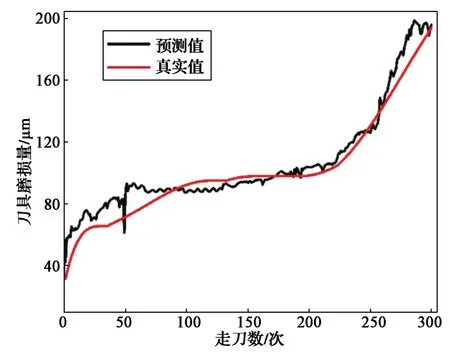
图10 铣刀磨损量预测结果Fig. 10 Tool wear prediction results

表3示出FE-LSTM铣刀磨损量预测模型与不同模型的对比结果。SVR，BPNN，CNN和FE-LSTM模型均可以实现铣刀磨损量的预测，其中SVR模型和BPNN模型属于传统的机器学习模型，无法保存时间序列数据较早时刻的信息并缺乏学习长距离依赖序列特征的能力。由表3可以看出，FE-LSTM铣刀磨损量预测模型与SVR模型和BPNN模型进行比较，MSE分别降低了67.07%和41.32%；与SVR模型相比MAPE降低了1.745%。与深度学习模型CNN相比，MSE降低了77.09%，MAPE降低了5.685%。实验对比结果证明，FE-LSTM铣刀磨损量预测模型优于传统机器学习模型和CNN模型，能更好地适应时间序列数据，从而更准确地进行铣刀磨损量预测。

4 结语

本文聚焦高速数控机床铣削过程中的铣刀磨损问题，提出了一种基于特征提取及长短期记忆神经网络（LSTM）的铣刀磨损量预测方法，主要采用时域分析、频域分析和时频域分析方法对传感器采集到的多通道原始信号数据进行特征提取，而后使用LSTM模型对提取后的信号特征数据进行训练，LSTM模型可保存时间序列数据中的时刻信息，并具备长距离依赖时间序列特征的学习能力且解决了RNN存在的梯度消失和梯度爆炸问题。实验结果表明，相比于传统机器学习模型，FE-LSTM铣刀磨损量预测模型可以实现对铣刀磨损量更为有效、精准的预测。后续将在自采真实数据集上应用此方法，以期解决实际工业问题；并将尝试引入Attention机制，以提升模型的并行能力以及更好地解决长距离依赖问题。