基于ARIMA模型的动力电池容量衰减不均衡预警
康祖超,熊 刚,王文明,钟雄武,周艳辉
(长沙中车智驭新能源科技有限公司,湖南 长沙 410000)
0 引言
动力电池作为新能源公交客车的能源核心,其性能与使用寿命直接影响车辆成本和行车安全。当前新能源汽车的动力电池必须将大量单体电池进行串并联使用才能满足汽车功率与电量的需求,而动力电池的性能与寿命往往受制于性能最差的单体,因此单体电池性能的不一致性严重影响了新能源汽车的使用[1]。
受工作环境及使用时间的影响,动力电池性能会发生不可逆的衰减,如内阻变大及容量衰减等。在由电芯单体组成的电池组中,容量符合“木桶原理”,即容量最低的电池单体表征了电池组整体容量,决定了整个电池组的能力[2]。所以,研究电池单体的容量估计及衰减在电池的预测性维护及循环梯次应用方面都具有重要的意义[3]。
目前常见的电池容量估计方法主要有基于电池荷电状态(state of charge, SOC)的估计方法[4]、基于经验模型(例如Arrhenius容量老化模型)的方法和基于充电状态的方法等。在国内,针对电池组容量、电压等参数不均衡的问题开展了众多研究,如文献[5]提出了一种基于可信度因子(C-F) 推理模型的分组均衡方法,文献[6]搭建了一种电感式均衡模型来达到模组间能量均衡的目的。同时,国外研究人员针对电池的不均衡性也提出主动均衡相关方法,例如基于电感的Buck-Boost法[7]。以上研究主要是从电池机理及主动均衡方面来降低因电池参数不均衡造成的影响。本文基于车辆大数据技术,针对电池容量估计精度不高的问题,采用高SOC下特征电压区间充电容量的衰减来表征电芯整体容量衰减的方法,进一步研究电池容量衰减的不均衡。
1 相关理论
1.1 特征容量估算法
动力电池的容量衰减主要是由于其活性物质损失而引起的。例如,依据电芯循环寿命测试结果和理论分析,磷酸铁锂电池容量衰减的主要原因是可用锂在负极的不可逆损失。对此,文献[6]提出了一种将完整的充电曲线和实验中的相应容量用作特定电池类型的训练数据来进行容量估算的方法,并采用粒子群优化的方式来确定最佳固定电压窗口。采用容量增量法分析电池充电容量特征变化时发现,在特定电压区间,其峰高、半峰宽和峰面积都发生了明显的衰减。图1示出电池充电在第100圈、300圈、1 000圈时通过容量增量法得到的特征曲线。可以看出,在峰1和峰2时段,波形基本一致;而在峰3时段,出现明显衰减情况。
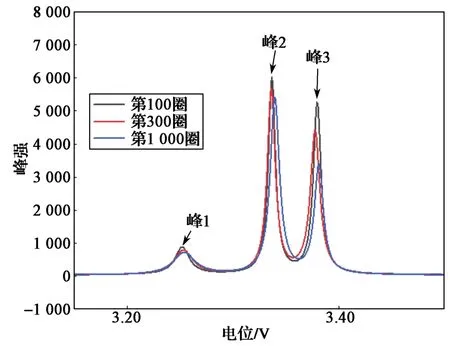
图1 电池特征容量充电曲线Fig. 1 Characteristic capacity charging curves
采用高斯回归式,见式(1),进行特征峰拟合,得到峰3:
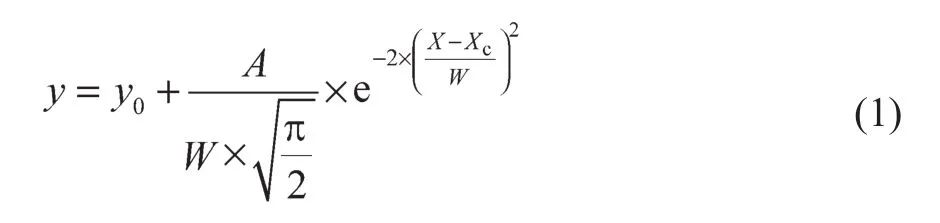
式中:A——峰面积;W——峰宽;Xc——峰中心位置。
如图2所示,在峰3时段的高斯拟合曲线能更加直观地显示出电池特征容量在充电情况下的衰减特征。因此可采用该特征峰的衰减代表充电曲线中高SOC区间充电容量的衰减。
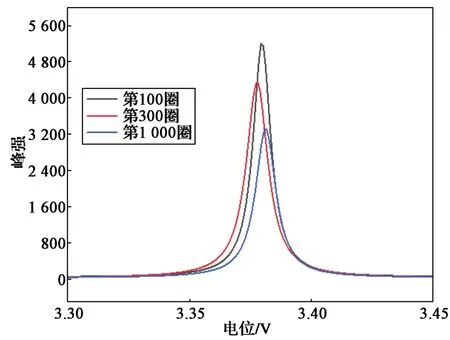
图2 充电容量峰3的高斯拟合曲线Fig. 2 Peak 3 charging capacity Gaussian fitting curve
本文以高SOC下特征电压区间充电容量作为电池容量的特征数据,并以该充电容量衰减来表征电芯整体容量的衰减,实现容量衰减不均衡预警的研究;采用特征电压区间的充电容量作为特征量,通过SQLite数据库实现数据存储。温度和充电电流的变化会造成特征电压区间的改变。在电压数据存在较大失真的情况下,通过改变特征电压区间来消除电流和温度的影响会造成很大误差。所以,采用等效静态电压模拟的方法将充电电压曲线进行归一化处理,过程如下:
(1)根据此时的温度、SOC和SOH(state of health)等值查表,获得等效内阻Rs。
(2)利用式(2)计算等效静态电压值。

式中:V和I——通过CAN总线获取的车辆电池电压及电流;Vos——等效静态电压。
在等效静态电压数据中,选取固定电压区间,通过安时积分法获得特征电压区间的充电容量。所选取的区间范围为

在充电模式下,当电池单体电压的等效静态电压值首次达到式(3)所示特征电压区间的下限时,开始进行电量累积;当特征电压超过式(3)的上限时,停止电量累积。非充电模式下,不触发电量累积。
电量的累积公式为

式中:Ii——i时刻的电流,Δti——i时刻的时间变化量。
1.2 ARIMA时间序列模型
由于特征电压区间的充电容量数据符合动力电池容量随时间的增加而衰减的时间序列特征,因此本文采用差分自回归移动平均(auto -regressive integrated moving average model,ARIMA)时间序列模型对采集的容量样本数据进行特征提取。ARIMA是一种针对非线性平稳时间序列的良好预测方法,其自回归滑动平均模型ARMA(p,q)模型的表达式如下:
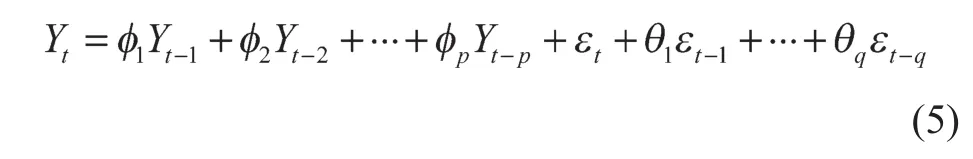
式中:p——自回归项数;q——移动平均项数;εt——白噪声序列;j与θk——模型参数,其中j=1, 2, …,p,k=1, 2, …,q。
ARMA(p,q)模型存在自回归形式模型(AR)与移动平均模型(MA)两种。
自回归形式模型如式(6)所示,其代表t时刻的电池容量值,由p个历史时刻值(Yt-1,Yt-2,…,Yt-p)的加权和得到。
移动平均模型见式(7),其在t时刻的电池容量由若干个白噪声的加权平均和组成[6]。
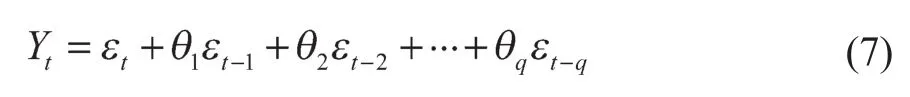
将 AR 与 MA 组合后,经过差分生成ARIMA(p,d,q)模型,其中d为使时间序列成为平稳序列所做的差分次数(阶数)。
2 ARIMA模型电池容量衰减不均衡预警方法
鉴于车载终端采用的特征数据具备时间序列特征,本文采用ARIMA模型作为特征数据的算法模型进行特征提取并实现预测,其实现流程如图3所示。
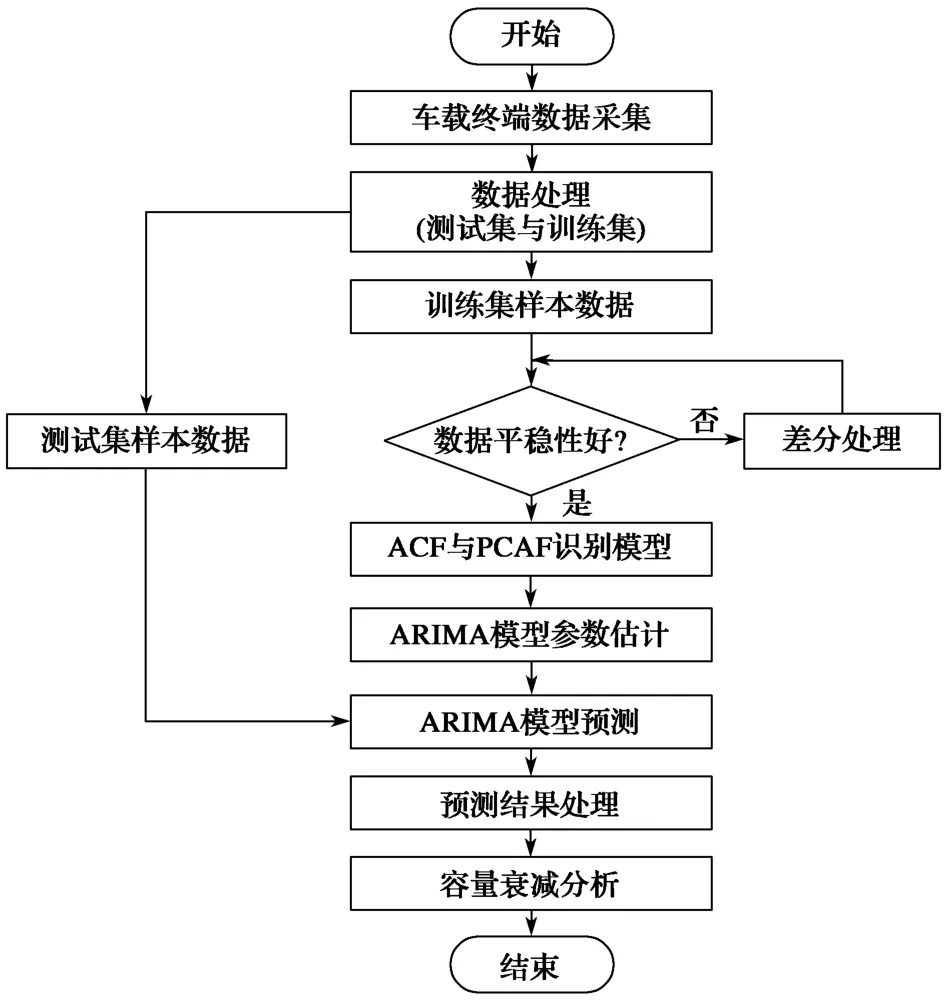
图3 基于ARIMA模型的电池容量衰减预警方法架构Fig. 3 Architecture of battery capacity attenuation early warning based on ARIMA model
基于 ARIMA 模型的电池容量衰减预警的详细步骤如下:
(1)根据特征容量的估算方式,通过车载终端的CAN通信网络,采集特定电压区间内的电池温度、电压、电流等基础数据,然后通过式(4)完成电芯单体容量的计算并存储到SQLite数据库;
(2)将存储到SQLite数据库中的数据读取出来并划分为训练集和测试集,训练集为前N个输入数据,测试集为第(N+1)个数据;
(3)构建训练集,对数据平稳性不好的数据进行差分处理,得到 ARIMA 模型的d值;
(4)根据时间序列的自相关函数(autocorrelation function,ACF) 和 偏 自 相 关 函 数 (partial autocorrelation function, PACF) 的截尾 /拖尾特性[8],确定ARIMA模型的p值和q值;
(5)根据已训练的 ARIMA 模型预测未来M个数据,得到预测的容量值;
(6)比较测试数据的真实值与预测值,得到预测的准确性结果。
3 实验验证
通过车载终端采集车辆实际运行中电池的电压、电流、温度、SOC和SOF等相关高精度数据,得到特定电压区间表征电池容量衰减的特征容量;利用ARIMA模型进行电池容量衰减不均衡预警,以验证模型的可用性。
3.1 数据采集及处理
本文以宁德时代锂电池为研究对象,在循环充电过程中,通过车载终端获取CAN总线上电池组186个单体的电压、电流及温度等相关数据并进行存储。CAN总线每50 ms获取一帧温度及电压等数据,每个电池单体的数据获取时间间隔在5 s左右,与云智通平台(车载终端上传数据的平台)采集数据时间间隔(10 s)相比,数据精度更高、数据量更大。
针对原始数据获取过程中存在的数据缺失情况,在Python环境下,采用Pandas库计算出该电池组已存在数据中的各个单体的平均值,并用该平均值进行数据填充。为了便于观察,这里以1号电池单体为研究对象,选取其某个月容量数据的平均值作为该月容量特征值,经处理后得到的数据如图4所示。动力电池的容量随着使用时间及充电循环次数的增加而明显减小,并且所得到的数据并不是平稳的时间序列,所以最终处理得到的动力电池原始数据不能直接通过模型进行处理,而是需要进行平稳性处理。
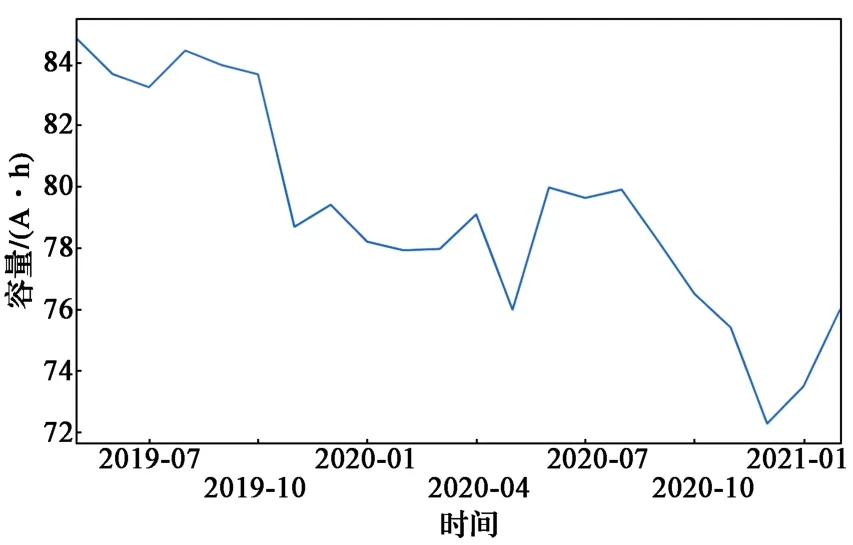
图4 1号电池单体容量Fig. 4 Capacity of the No. 1 battery cell
3.2 数据平稳性处理
采用ARIMA模型进行电池容量衰减预警的前提是作为训练集的时间序列必须是平稳序列。目前,对平稳序列判断的传统方法是采用图形判断,该方法很大程度上存在主观臆断,判断误差大。另外,图形判断实际上是直观判断数据是否是随机序列,并不是严格的平稳性检验[9]。最为科学的平稳性检验方法是单位根检验。单位根检验包括DF(dickeyfuller)检验、ADF(augmented dickey-fuller)检验等[10]。本文选择ADF方法检验训练集数据的平稳性,分别对训练集本身及其一阶差分进行检验。训练集作累加后的数据及其一阶差分作ADF单位根检验的结果如表1所示。
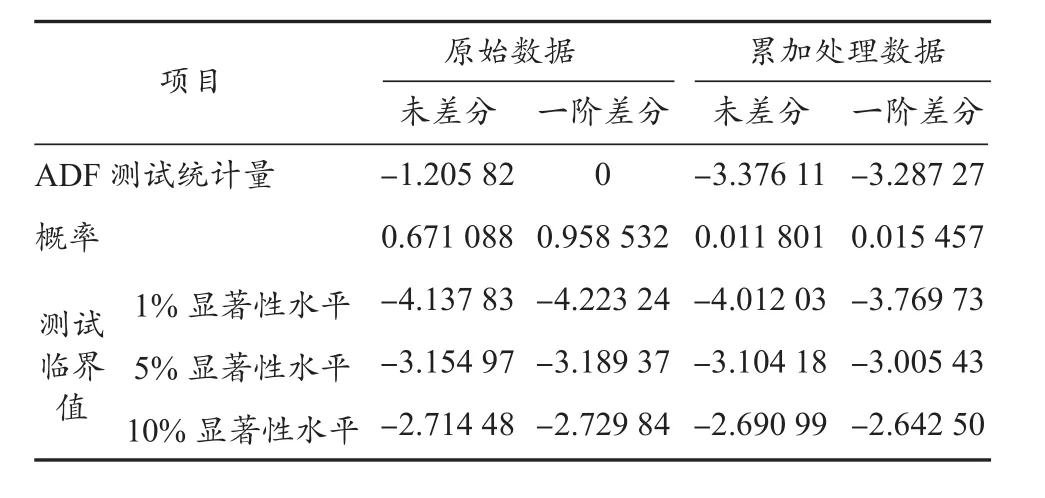
表1 训练集数据平稳性校验Tab.1 Test set data stationarity verification
通过ADF校验发现,一阶差分处理后,原始数据的ADF测试统计量大于1%,5%和10%的这3个阶段的显著性水平,且概率值较大,所以原始数据即便通过一阶差分处理,也无法用于ARIMA模型的训练过程;而在原始数据的基础上进行累加处理后,数据的平稳性增强。考虑到所有单体的普适性,本文针对累加处理的数据进行一阶差分处理后再作为模型的数据集校验。检验结果显示,其ADF测试统计量均小于5%显著性水平的,且概率值较小,只有0.01左右的概率支持该假设, 即拒绝存在单根假设。因此,可认为该数据一阶差分后为平稳时间序列,能够应用于 ARIMA 模型。
3.3 模型参数估计
经过平稳性处理后,累加处理后数据的一阶差分数据的ACF与PACF系数如图5所示。可见,ACF与PACF均拖尾。根据最小化原则,采用Pandas库中的idxmin方法找到最小值位置,最终确定ARIMA(3, 1, 0)为最优模型参数。
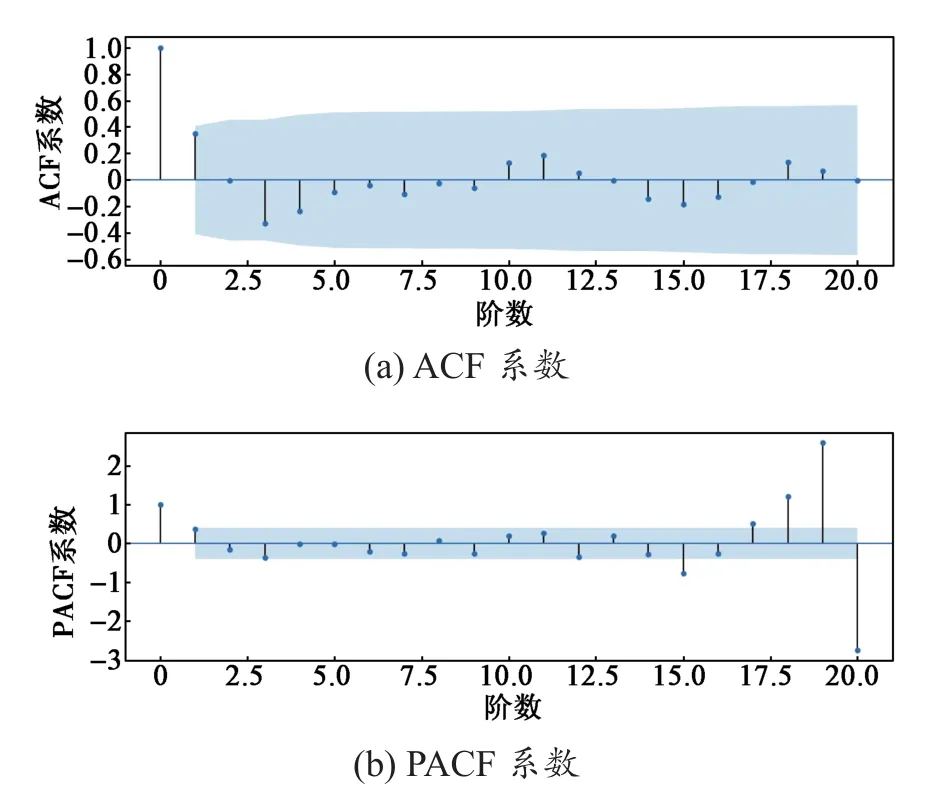
图5 累加处理数据一阶差分序列ACF与PACF系数Fig. 5 ACF and PACF coefficients of the first-order difference sequence of accumulate processed data
4 电池容量衰减预警应用实例
采用上文确定的最优模型参数ARIMA(3,1,0)对电池容量进行预测,通过C语言在终端上进行ARIMA模型的复现,在终端上完成数据保存及模型预测,以实现电池容量预警功能。具体的应用实现流程如图6所示。
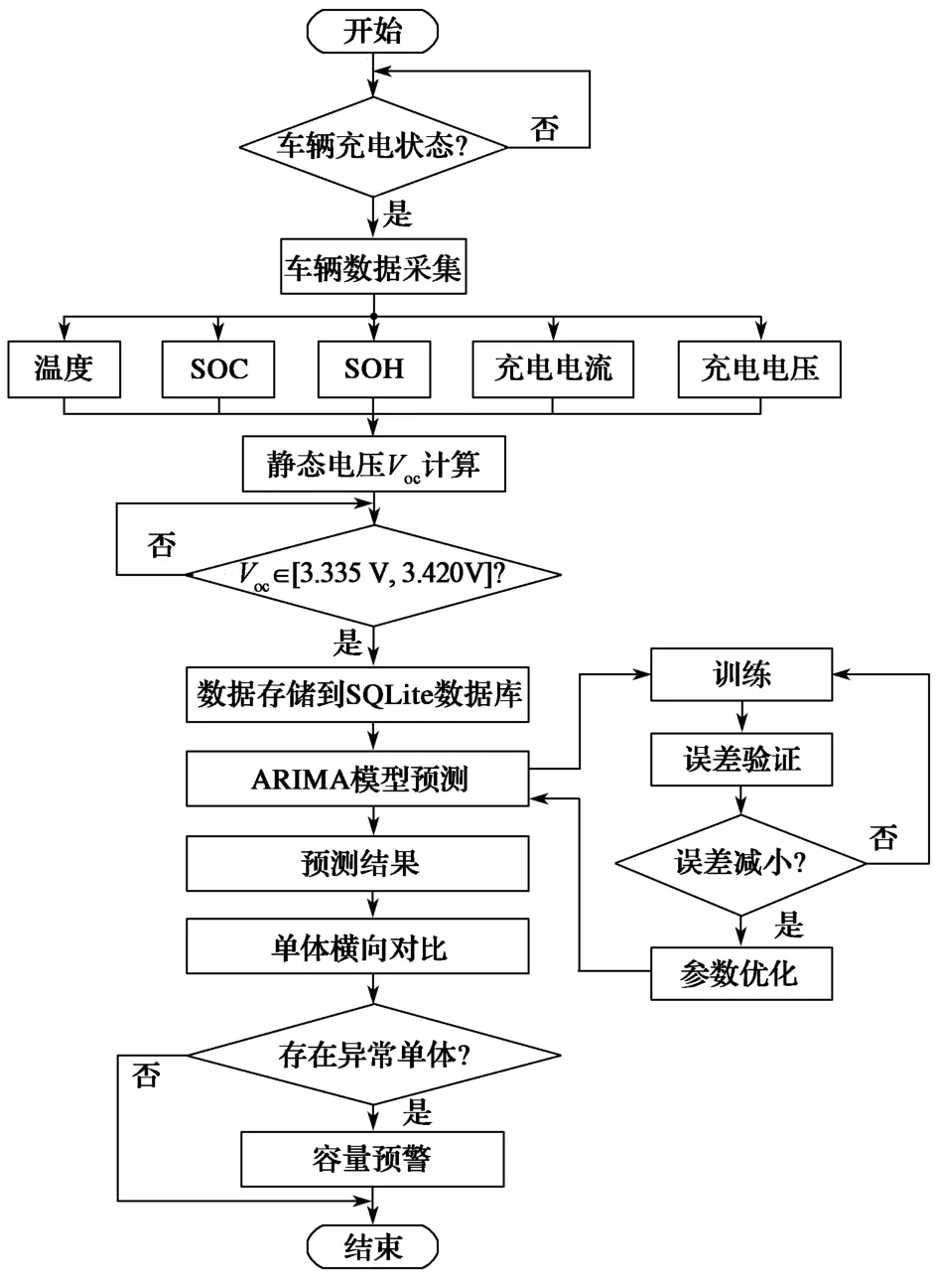
图6 系统应用框架Fig. 6 System application framework
车载终端采用Linux操作系统环境,并采用C语言实现数据采集、特征容量的计算及数据结构化存储。ARIMA模型通过C语言复现运行在车载终端上,将模型参数p,d,q初始化为上述最优模型参数。终端通过对模型得到的预测值进行横向对比来完成电池容量不均衡单体的筛选,并实现不均衡报警功能。模型的自训练功能是指用当前实际采集值与模型预测得到的预测值相比较得到误差值,并将其与现有模型误差进行对比,取误差较小的模型参数进行模型优化更新,得到最优模型参数,作为下次模型预测的输入参数。
模型预测过程中采用滑窗的方式进行模型的训练和测试,其最终的预测结果如图7所示。
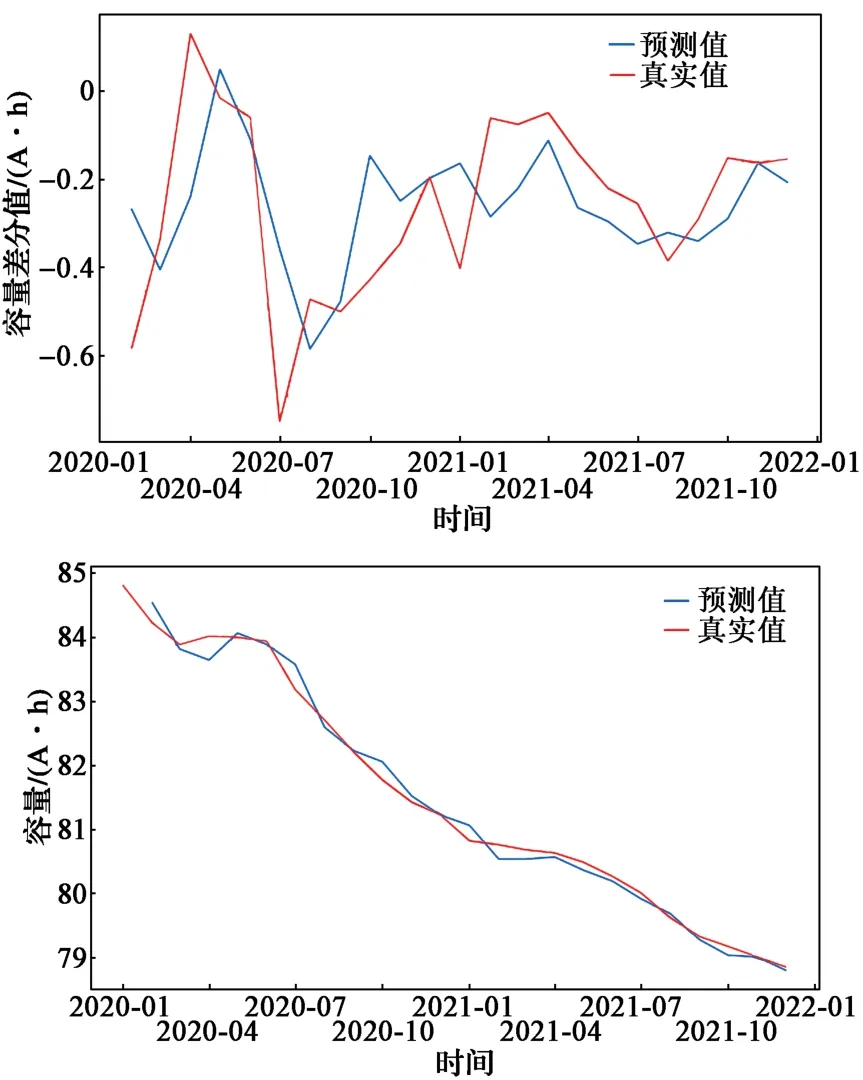
图7 1号电池单体容量累加值及其一阶差分预测验证结果Fig. 7 Accumulated value prediction of No. 1 battery cell and verification offirst-order difference prediction
根据电池组各个单体的一致性特点,其他单体理论上与1号单体的衰减趋势相同,可采用相同模型参数完成各个单体的验证,并将数据分为24个月的样本数据,采用前23个月的数据预测第24个月的容量数据,其结果如图8所示。
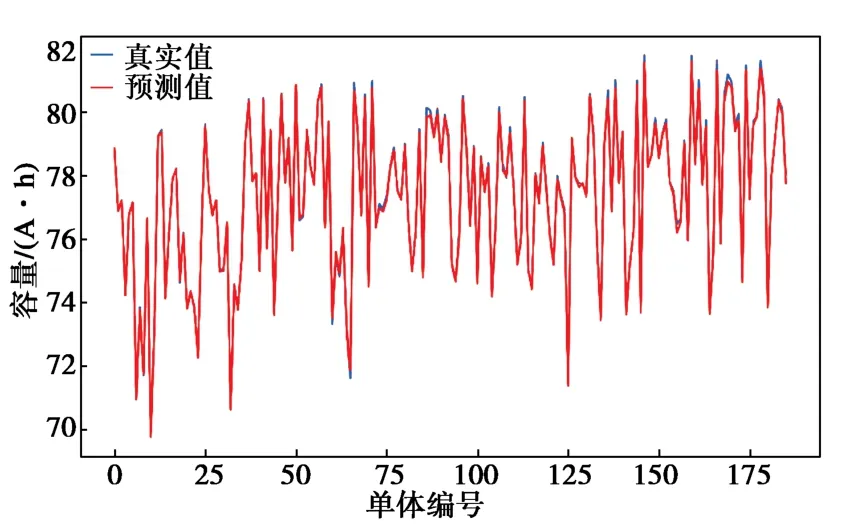
图8 电池各单体真实值及预测值Fig. 8 True value and predicted value of each battery cell
由图8可得,模型的预测结果与实际值基本重合。模型预测的各个单体标准误差如图9所示,预测值与真实值之间标准误差小于0.6 A·h,并且普遍分布在0.2 A·h左右,可用于模型衰减预警功能实现。可见,该模型训练参数及预测结果符合绝大多数单体的衰减变化规律。考虑模型的训练成本,选择一年以上的样本数据量来实现容量衰减预警功能。
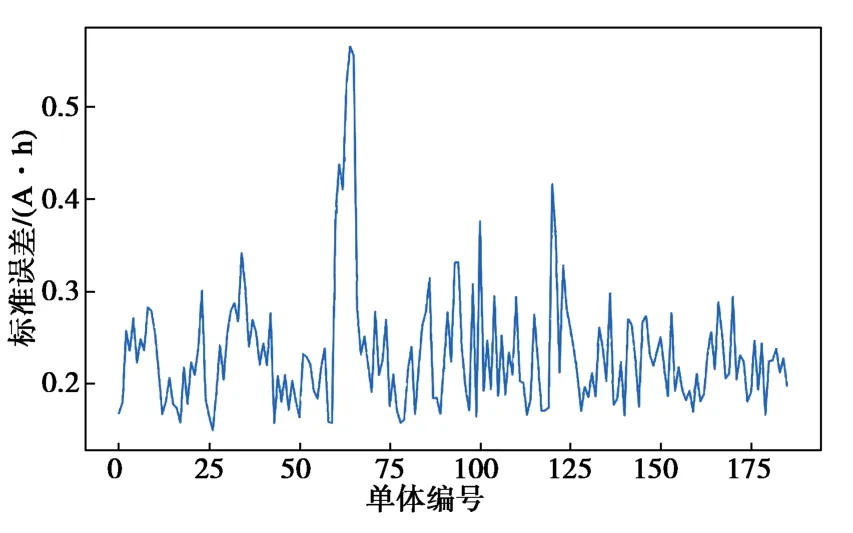
图9 ARIMA模型预测标准误差Fig. 9 Standard error of prediction with ARIMA model
图9中个别单体因存在某段时间衰减规律异常而导致的模型误判,需要在下一次预测之前进行验证,并对历史数据采用平均值替换的方式进行修正。即通过横向对比的方式挑出异常单体,进而实现系统的容量衰减预警功能。
5 结语
本文针对新能源公交客车动力电池容量衰减不均衡问题,采用ARIMA时间序列模型进行预测,通过对车载终端获取的充电循环过程中代表电池容量的高精度数据进行分析,得到了如下结论:
(1)基于电池充电机理,采用充电循环过程中特定电压下突出反映容量变化的特征数据进行分析,减弱了不相干数据对电池容量预测的影响,同时降低了模型的训练复杂度。
(2)采用累加处理的结果作为模型的输入,既能反应容量的整体情况,同时也能使数据的一阶差分值更加符合模型的输入需求。
(3)基于ARIMA时间序列模型的电池容量衰减预警,可有效解决小样本、快速与模型准确性问题,预测结果标准误差小于0.6 A·h,普遍误差分布在0.2 A·h左右,能够有效地预测未来一个月电池容量的衰减情况,具备实用性。
(4)ARIMA时间序列模型复杂度低、计算效率高,在服务器上部署较为简洁,不会占用服务器的大量计算资源,适用于车辆动力电池容量衰减批量预警;同时便于车载终端上的算法集成,为车辆的预测性维护提供相应解决方案。
(5)ARIMA模型对输入数据平稳性有较高的要求。实验验证结果表明,在短期内,ARIMA模型在电池容量衰减预警样本数据上具有较高的预测精度和较强的适应能力。但当前的ARIMA模型不能直接用来解决电池其他类型故障的预测,尤其是变化规律复杂的故障,对这些类型故障的预测需要借助更高级的方法和理论。

