基于短时频谱与自相关特征的雷达脉内调制识别
童 真,姚 群,高墨韵,柴 恒
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
雷达调制识别是电子侦察的重要环节,通过对波形的处理分析,获知敌方雷达的性能参数与威胁程度,为后续个体识别与电子对抗提供了作战支撑。国内外对雷达脉内调制识别问题做了大量的研究,一类学者从雷达调制的特点出发,针对性地提出了瞬时频率法[1-2]、时频变换法[3]、小波变换法[4]等,并依照这些特征参数制定了相关的分类流程。另一类学者借助了神经网络特征提取与分类的能力,文献[5]、[6]将波形时频变换的结果视作图片分类问题,使用卷积神经网络进行特征提取与调制分类,文献[7]、[8]对原始波形进行归一化处理,并以此作为输入,使用循环神经网络进行特征提取与分类。第一类方法需要较高的专业知识,制定复杂的处理流程,花费较长的开发周期,面对现代雷达技术的迭代更新,难以快速跟进。第二类方法可以缩短模型更新周期,但是神经网络作为“黑箱”,研究人员难以把握其运行机制,相对第一类方法非常依赖训练数据,容易造成过拟合且泛化性能欠佳。
从雷达波形调制的机理出发,以短时频谱变化特征与自相关统计特征作为前端输入,用以表达雷达调制中频率变化与相位变化的特性,并且后端采用长短记忆网络,用以提取脉冲时序变化特性,从而避免盲目采用神经网络,最终在多种信噪比与不同脉宽的情形下,获得了较高的分类准确率与较好的泛化性能。
1 脉冲调制特征
提取截获雷达脉冲的特征,旨在表征各种调制方式的频率变化与相位变化特性。雷达信号处理流程涉及射频信号下变频、中频信号采样、数据分析,在此基础上分别进行雷达信号的建模与频谱相位的特征分析。
1.1 雷达信号建模
设定窗口大小与滑动步长,对不同脉宽的雷达中频信号进行截断与分帧,任意窗口t中的离散采样信号可以表示为:
yt[n]=xt[n]+z[n]=Acos(ωt(nTs)+θt)+
z[n],n∈{0,1,…,N-1}
(1)
式中:xt[n]为窗口t中的信号成分;z[n]为加性高斯白噪声,方差为σ2;Ts为采样时间间隔;ωt为窗口t中信号的频率;θt为窗口t中信号的相位;N为窗口的长度。
假设雷达脉内信号的幅度A保持不变,而在频率ωt与相位θt2个维度进行调制与编码。在任意窗口t中,频率ωt变化有多种情况,可能保持固定,或者发生缓慢变化(如线性调频),或者在码元分界处发生跳变(如频率编码)。同理,窗口中相位θt可能保持不变,而在码元分界处跳变(如巴克码)。因此,对各帧信号进行统计与分析,可以刻画出雷达信号的调制与编码特性。
1.2 频谱变化特征
各帧信号的频谱变化可以反映出调制的频率特征与相位特征。首先,对各帧信号添加窗函数,进行离散傅里叶变换,然后计算各帧频谱峰值对应的频点,提取信号频率调制的特征。对窗口帧t进行离散傅里叶变换,其中频谱频点m的值表示为:
(2)
式中:w[n]为窗函数,可选用汉宁窗、海明窗、布莱克曼窗等。
假设频谱幅度峰值对应的频点为mk,结合邻近mk-1与mk+12个频点的幅值,根据文献[9]中方法,采用二次曲线进行拟合,得到实际频谱峰值的偏移为:
(3)
从而帧t中谱峰的频点可以近似为:
(4)
为了提高频谱特征的泛化性能,本文不直接将式(4)作为信号的频率特征,而是考虑各帧谱峰对应频点的变化情况,引入下面2个动态差值,作为帧t的频谱特征:
(5)
(6)

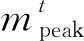
此外,还引入功率谱估计的3 dB带宽作为各帧t频率相位变化的特征,表示如下:
(7)
式中:Pt[m]=|Xt[m]|2;f(*)为指示函数,条件满足时为1,否则为0。
各帧的3 dB带宽可用于描述信号频率变化的幅度,特别是面对大斜率的线性调频信号。同时,对于相位调制信号,由于帧内码元分界处相位跳变造成信号不连续,引起频谱能量扩散,从而造成某些帧的3 dB带宽发生变化。
1.3 自相关变化特征
脉内各帧信号的自相关变化可以描述调制的频率与相位特征。采用补零的方式计算各帧信号的自相关,由于自相关是对称的,因此只考虑自相关的正半轴,以常规连续波信号的自相关作为基准,其计算如下:
(8)
忽略上式中白噪声引入的冲击函数项,得到常规信号的自相关包络是斜率为负的直线,其自相关中各点的方差为:
(9)
为了能够衡量各帧信号的自相关特征,对信号长度N进行归一化,表示如下:
(10)
对于频率调制与相位调制的信号,在1帧中出现频率或者相位的跳变点,会造成自相关函数向零点集中,一般而言会获得更低的方差特征。理想情形下,相对于常规连续波,有调制的波形(例如13位巴克码),1帧信号相当于1段码片,可以视为1段2位或3位巴克码,相比连续波,自相关的旁瓣会更低,因此方差减小。以连续波为基准,计算式(10)为1,由此可以作为一个判别依据。
同理,引入帧t自相关的峰度信息作为高阶统计特征,用来衡量信号自相关的集中程度,表示如下:
(11)
其中峰度的计算方式为:
(12)
同样地,以常规连续波作为基准,结合式(8),得到其峰度值约为-0.3,并以此作为信号频率与相位变化的一个判别指标。
1.4 调制特征提取流程
首先对雷达信号进行归一化与分帧的预处理,然后计算各帧的频谱变化特征与自相关统计特征,由此描述信号调制的频率与相位变化,作为后续分类器的判别基础。雷达信号的频谱与自相关特征提取流程概括如下:
步骤1:对雷达中频采样信号进行均值方差的归一化处理,使其均值为0,方差为1;
步骤2:对归一化后的信号进行分帧,每一帧的采样点数为N,帧间滑动步长为N/2;
步骤3:选取窗函数,减少能量泄露,依次对每一帧信号进行离散傅里叶变换(DFT),由于是实信号,仅考虑半边谱,得到频谱幅值与功率谱估计;
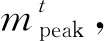

2 分类网络构建
在获取信号频谱变化与自相关统计特征的基础上,考虑雷达信号长短脉宽不同,借助长短记忆网络,进行雷达信号的分类识别。数据输入从2个角度考虑:一是依次输入脉内各帧信号的频谱与自相关特征;二是直接输入原始中频数据,通过网络学习特征,借此测试2种数据输入方式的泛化性能。
2.1 长短记忆网络
借助长短记忆(LSTM)网络处理不同脉宽信号的调制识别问题,依次输入每帧信号的频谱与自相关特征,单个帧的特征记为:
(13)
由此构成输入序列:
X=(s1,s2,…,sT)
(14)
式中:T为整个脉冲的分帧数量,因此输入序列的维度为X∈T×5。
LSTM网络在脉冲的最后一帧做一次分类识别,采用多对一模式,即多个时序的特征作为输入,具体为从1到T时刻,最终在T时刻生成一次分类识别结果。
这里采用单层单向LSTM网络作为主体,设置LSTM层中单元数量为128,LSTM层的后接一层全连接,将维度映射到雷达调制的种类数,最终通过Softmax进行分类。下面的表达式描述了LSTM网络的构架与权值参数:
mT=LSTM(s1,s2,…,sT)
(15)
pT=Softmax(Wfc1mT)
(16)
式中:Wfc1为全连接层的权重参数。
LSTM层采用tanh作为单元状态的激活函数,采用sigmoid作为输入、遗忘、输出门的激活函数。LSTM层中与输入、循环、偏置权重相关的前向传播与反向更新的过程,参考文献[10],这里不再赘述。
2.2 直接脉内数据输入
为了验证频谱与自相关特征的效用与泛化性能,采用直接中频数据输入的方式作为对照,为此仅对每帧信号进行均值方差归一化,而不包含信号任何频谱与自相关特征。记每帧原始中频数据构成的输入序列为:
Z=(r1,r2,…,rT)
(17)
式中:Z∈T×N,N为每帧中采样数据点数;r1,r2,…,rT为原始采样数据,维度为N。
本节网络的LSTM层采用与上节中LSTM层相同的单元数量,仅在LSTM层之前添加一层全连接,降低原始数据rt的维度,同时增加网络的非线性,如下所示:
(e1,e2,…,eT)=relu(Wfc0Z)
(18)
式中:e1,e2,…,eT为原始数据Z激活后的特征向量。
本节设置的网络通过前置的全连接层,将输入的原始帧的数据映射到32维,能够降低参数量,同时获得较高的训练正确率。前置的全连层进行特征变换后,得到式(18)所示的输入序列,为了控制变量,后续的网络结构与上节网络相同。
3 测试与性能分析
3.1 数据集构建
实验采用实际雷达信号,雷达脉冲包含4种调制方式:常规雷达信号(NS,连续波),线性调频(LFM),非线性调频(NLFM),13位巴克码(BPSK)。数据集分为训练验证集与泛化测试集,其中泛化测试数据集采用与训练测试集相同调制模式,但是其载频、带宽等参数完全不相同。训练验证集的雷达调制参数、脉宽、信噪比如表1所示,总计13 210条数据。泛化测试数据集包含线性调频与常规雷达信号2种调制模式,其中线性调频的载频、带宽、斜率方向、脉宽是训练集中没有出现的,控制2种调制模式的数量比为1∶1。泛化测试集的具体参数如表2所示,总计4 130条数据。
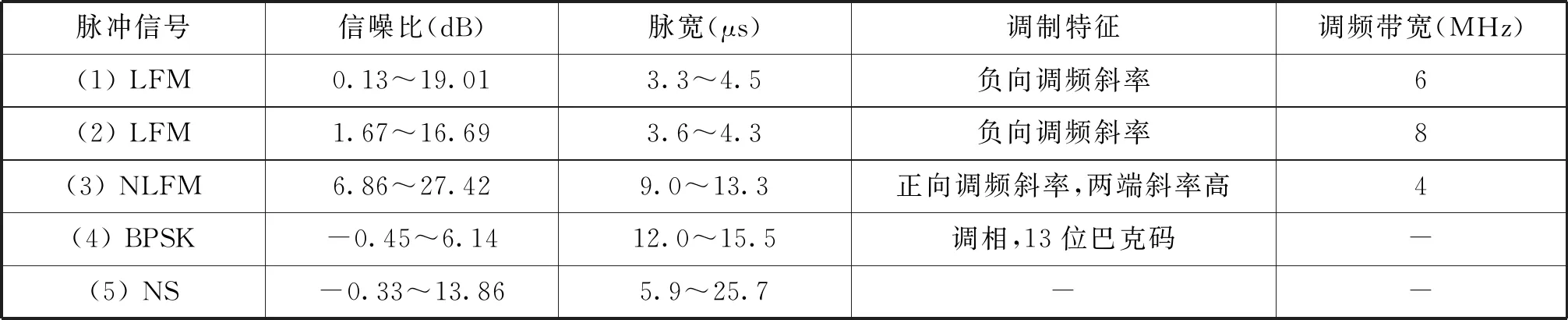
表1 训练验证集雷达脉冲参数

表2 泛化测试数据集雷达脉冲参数
3.2 训练与测试
分别训练2种输入的分类网络,为了便于区分,将采用频谱与自相关特征作为输入的网络记为feat-lstm,对于直接采用均值方差归一化中频数据的网络记为raw-lstm。设置每帧窗口N为1 024个信号采样点,滑动步长设为512,因此对于feat-lstm网络,输入是若干维度为5的频谱自相关特征帧,对于raw-lstm网络,输入是若干维度为1 024的归一化中频数据。网络训练使用的框架是Keras,优化器采用adam,学习速率设为0.001,由于样本的脉冲长度不同,batch大小设为1,有利于提高训练的准确度。训练时发现,epoch数量设为2或3,即可以获得较高的准确度。如表1中数据集所示,训练集整体信噪比范围在0~27 dB之间,脉宽分布在3~26 μs之间;测试集的信噪比范围是3~18 dB,脉宽分布在3~15 μs与60~90 μs两个区间。对于上述2种采用不同输入的网络,其训练与测试的整体正确率如表3所示。

表3 2种不同输入网络的分类性能对比
3.3 结果分析
采用频谱自相关特征的网络与采用直接中频数据的网络,两者具备相似的训练正确率,表明网络能够充分地拟合数据分布。然而,采用直接中频数据输入的网络,在面对不同载频、带宽等调制参数的信号时,泛化能力较差,正确率仅为52.03%;而采用频谱与自相关特征作为输入的网络,其测试正确率为90.46%,泛化性较好。2个网络的主体都为单层LSTM结构,且隐含单元数都为128,以上结果表明仅依靠lstm结构并不能很好地提取雷达信号的调制特征,泛化性能差且造成训练集上严重的过拟合现象。
对于采取2种不同特征作为输入的网络,本文给出了各自在多种信噪比(SNR)情形下的分类性能。图1展示了测试集中2种输入对于常规脉冲NS的分类性能,图2展示了测试集中两者对于LFM调制的分类正确率。如图1所示,两者对于常规脉冲分类的准确率都维持在较高水平。特别地,对于采用频谱自相关特征的网络,其在多种信噪比下分类的正确率接近100%。如图2所示,对采用与训练集中不同调制参数的LFM信号,采用直接中频数据的网络分类的准度较低,具体正确率仅为20%左右,未能在训练集中提取到有效的调制特征,泛化性能差。作为对比,采用频谱自相关特征作为输入的网络,在低信噪比3~6 dB范围内,分类正确率为60%,在信噪比6~15 dB之间,正确率为80%左右,在高信噪比15~18 dB之间,分类正确率接近100%。综合上述表现,以频谱与自相关作为特征,具备较好的分类正确率与泛化性能。
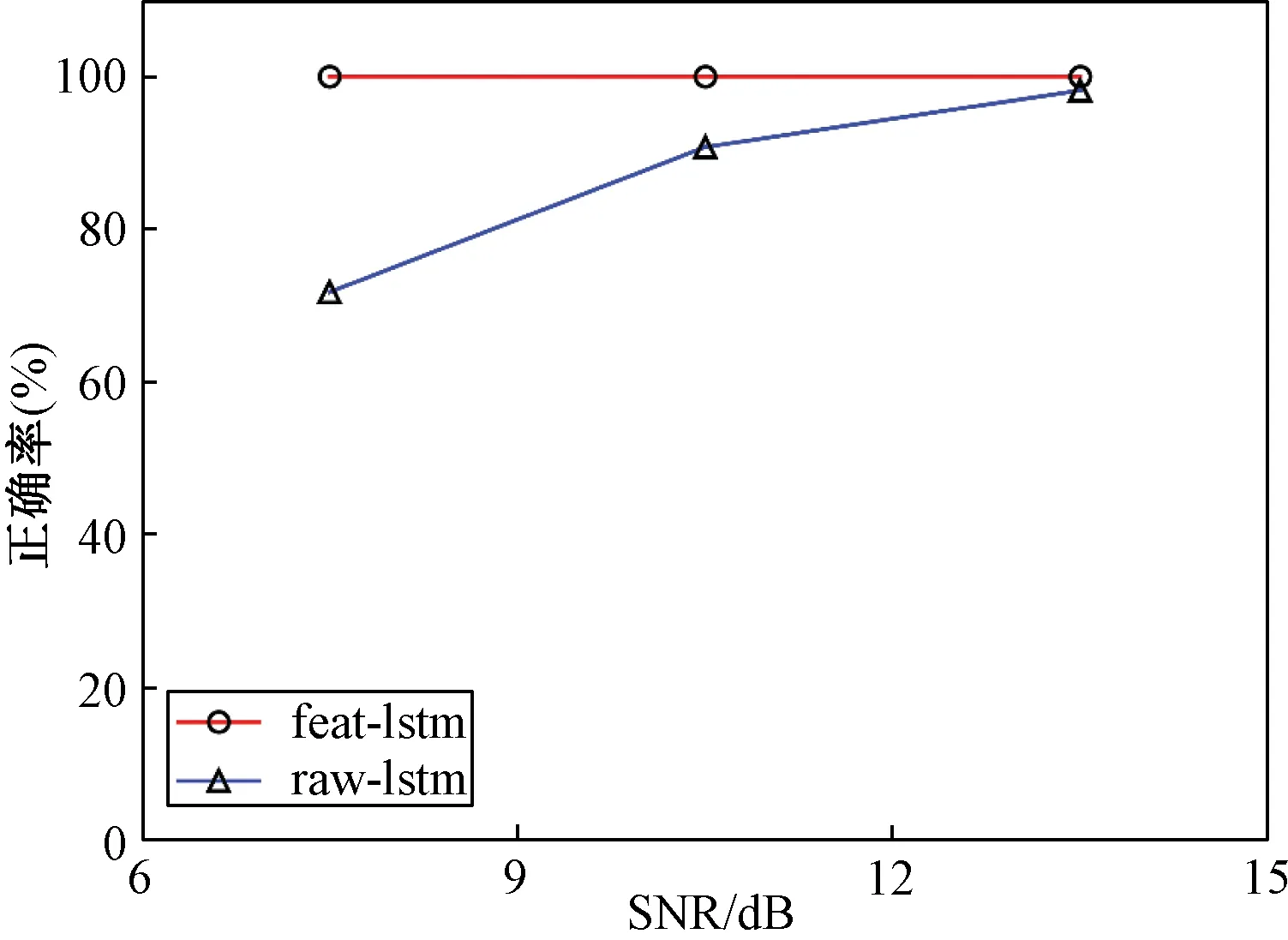
图1 2种输入在不同SNR情形下对常规NS信号的识别性能
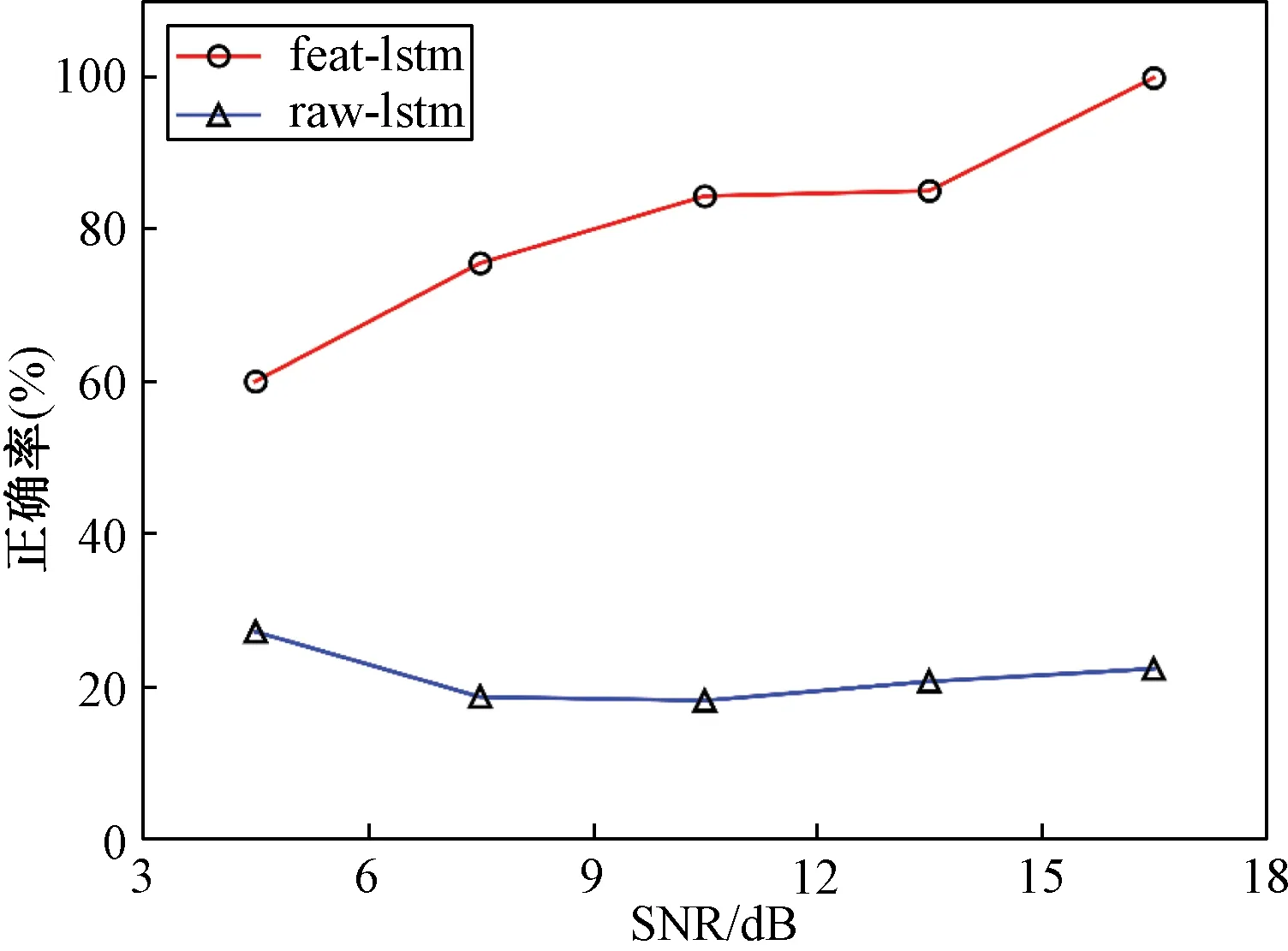
图2 2种输入在不同SNR情形下对LFM信号的识别性能
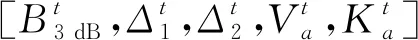
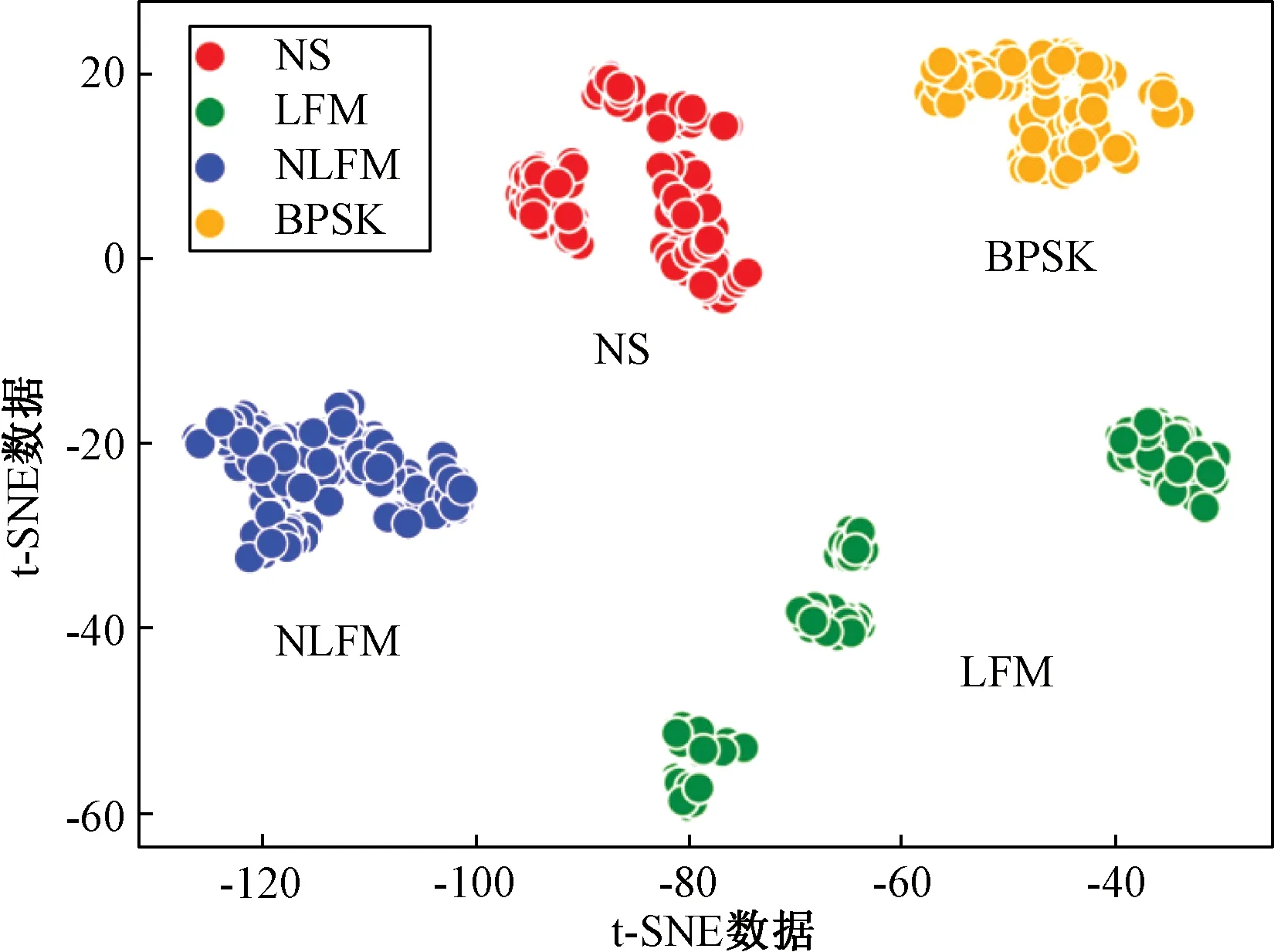
图3 各类调制频谱与自相关特征的可视化效果
4 结束语
通过提取短时频谱与自相关变化作为前端特征输入,后端采用长短记忆网络用以提取脉内帧间的时序变化特征,并最终输出雷达脉内调制的识别结果。在大范围信噪比、脉宽的场景下,通过雷达数据的测试验证,本文提出的方法能够获得较高的调制识别准确度,具备较好的泛化性能。

