基于卫星外辐射源的高精度单站定位方法

窦修全

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.河北省电磁频谱认知与管控重点实验室，河北 石家庄 050081)

0 引 言

隐身、电子对抗、低可截获通信和反辐射等技术的不断发展，给有源雷达探测预警系统带来较大的挑战，而基于外辐射源的雷达[1-2]探测具有独特的优势，可与有源雷达优势互补，具有良好的战略战术价值和应用前景。目前外辐射源雷达[3-5]多基于地面广播、电视等外辐射源目标探测的定位方法，其探测范围受限于波束覆盖范围、定位精度等因素的影响，难以满足远海作战和态势获取的需求。而通信/导航卫星等天基辐射源具有全球覆盖、全天候存在、多辐射源空间分布、信号带宽宽等优点，随着未来用户需求的不断提高和卫星制造技术的不断升级，其所需信号功率和带宽不断提高，使利用卫星作为外辐射源的侦测系统具有较大的发展潜力。

目前外辐射源定位常用的体制有多侦测站时差[6-8]、多外辐射源单站时差[9-11]等，均分析了定位方法的可行性以及所能达到的定位精度[12-14]和定位区域分布等，但是该定位体制未考虑实际的应用场景和系统的可实现性，致使定位方法性能得不到发挥。外辐射源探测体制多用于实现远距离目标侦察，方位角具有较大的变化范围，而俯仰角只有较小的变化范围，这导致外辐射源定位系统通常只给出方位角信息，不能给出二维测向信息，致使目前研究的单站二维测向时差定位模型无法应用于实际工程中。而基于多站的外辐射源定位系统虽然技术可操作性好，当实际中考虑到系统布站共视问题，同时考虑系统间协调工作、数据传输等问题，其会导致定位系统复杂，不宜灵活开展目标侦察定位。

本文针对实际的应用场景及系统侦察信息，提出了基于外辐射源的单站一维测向时差定位模型，将侦察目标高度信息转换到地球表面方程[15]中，实现目标二维测向方程简化，结合时差方程完成外辐射源定位模型的构建。采用牛顿迭代处理实现目标位置的精确解算，新定位模型对测量噪声具有较强的稳定性，能够达到较高的定位精度，通过仿真试验验证了改进的定位模型具有较佳的定位性能。

1 定位模型分析

基于卫星外辐射源的目标定位场景如图1 所示，该应用场景主要实现远距离高空目标侦察定位。由于目标距离定位站较远，俯仰角测量范围通常在2°～5°间，出于系统成本考虑，目前系统采用一维测向体制，无法采用俯仰解算方程解算目标位置，为此假定目标位置高度为一定值，不考虑基于俯仰角的定位方程，将目标高度设定为定值，通过建立目标地球方程，实现目标方向降维处理。

图1 定位体制示意图

设目标在地心直角坐标系中的坐标位置为(x,y,z)，考虑目标具有一定的高度，因此其在地心直角坐标方程中的关系式为：

(1)

式中：h为目标相对地面的高度信息;Rl为地球半径;e为地球曲率。

卫星信号经过目标反射到达接收机的路径与直达波信号路径间的时延信息中隐含了目标位置信息，因此时延信息间接反映了卫星、目标、地面接收机间的位置关系，并可建立时延表达方程：

(2)

该时延方程说明了路径传输时延与目标位置、卫星位置、接收站位置的关系。

根据目标与地面侦测系统方位相对位置关系，建立目标方向方程：

tanβ=(y-y1)/(x-x1)

(3)

该表达方程实现了测向信息与目标位置、接收站位置的关联。

利用隐含目标位置的3个方程完成目标运动状态的描述，通过3个表达方程实现目标位置解算，对表达式(1)、(2)、(3)进行变形处理得到目标解算表达方程组：

(4)

方程(4)中所涉及的3个定位解算方程中，时差表达方程和目标位置地心直角坐标表达方程采用WGS-84坐标系，测向表达方程采用的是地球表面坐标系，因此在采用牛顿迭代处理中需要将坐标方程进行转换，将测向方程的迭代处理中间结果转换到WGS-84坐标系中，实现定位解算方程参数统一，保证牛顿迭代处理的正确性。

1.1 牛顿迭代解算处理

首先根据设定的目标位置初值计算函数矩阵：

(5)

分别对f1(x,y,z)、f2(x,y,z)、f3(x,y,z)3个定位方程求导，计算定位方程(4)雅克比矩阵：

J(Pk)=

(6)

利用以上求得的雅克比矩阵，求解线性方程组，具体迭代处理过程如(7)～(9)所示，实现目标位置优化解算：

J(Pk)ΔP=-F(Pk)

(7)

ΔP=-J-1(Pk)F(Pk)

(8)

Pk+1=Pk+ΔP

(9)

通过式(10)中的前后2次迭代计算得到的定位结果的位置变化判断迭代是否终止，其中ε为一正小数。

norm(Pk+1-Pk)<ε

(10)

根据以上分析及定位结果推导，可以确定基于卫星外辐射源的单站测向时差定位方法的详细处理步骤如下：

步骤2：根据该初始位置，结合第i次迭代中时差测量得到的时差值ΔT和方向正切值tanβ，由公式(4)构造对应的函数矩阵F(Pk)。

步骤3：并根据式(7)、(8)、(9)得到下一次迭代中目标位置的估计结果Pk+1。

步骤4：定义相邻2次目标位置的距离δk=norm(Pk+1-Pk) 为迭代处理的代价函数，若δk小于某个设定的门限值，则停止迭代并输出定位结果；否则，令k=k+1，并返回步骤2，继续下一次的迭代处理，直至δk小于设定门限值。

步骤5：解算得到当前测量条件下的目标位置，并将WGS-84坐标系下的位置转换到地球表面坐标系，即得到目标经纬度信息。

基于测向时差的单站定位算法处理流程如图2所示。

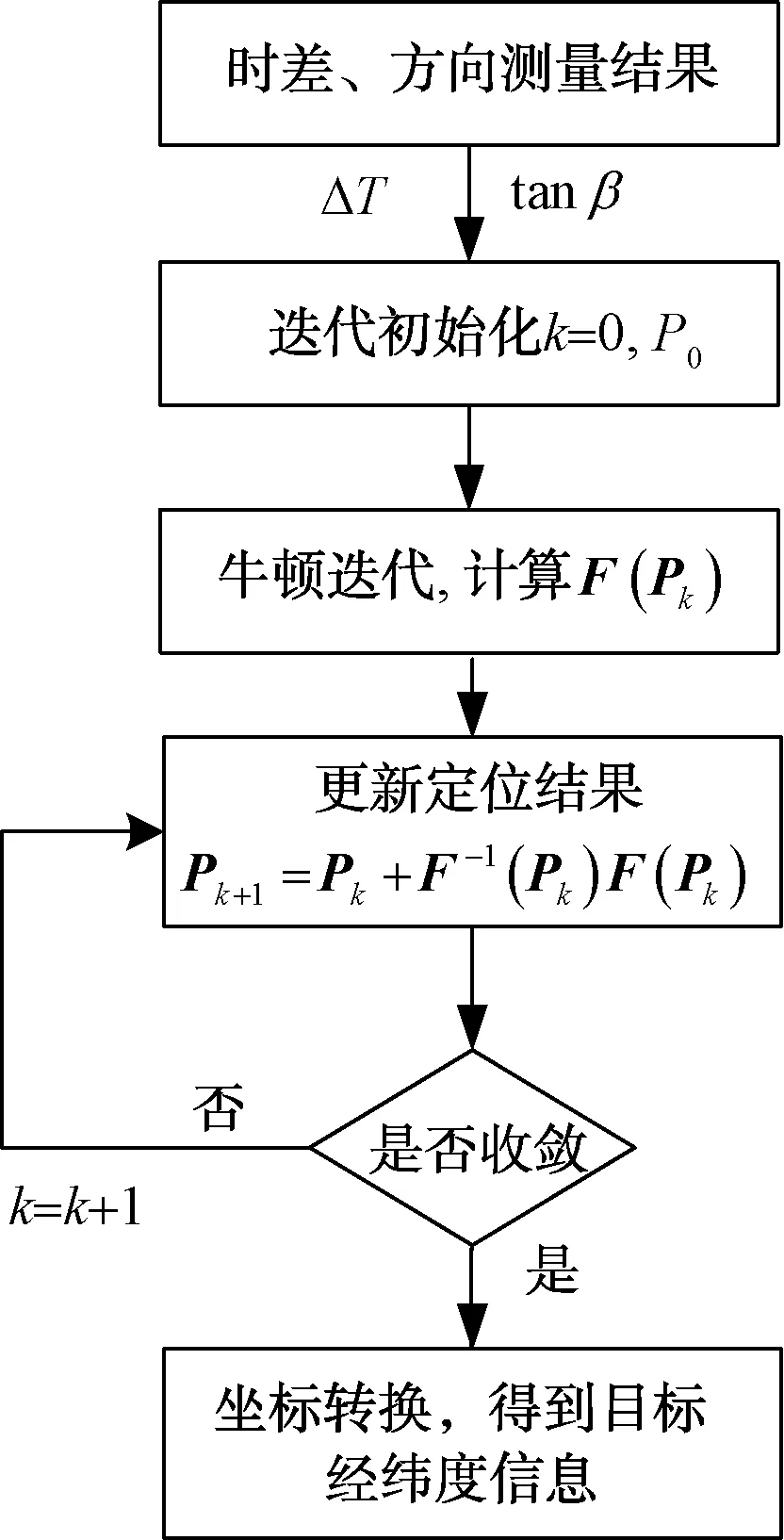
图2 基于测向时差的单站定位算法处理流程

1.2 导数关系推导

实现目标解算，需要由式(4)分别对f1(x,y,z)、f2(x,y,z)、f3(x,y,z)进行求导计算构造雅各比矩阵。

其中函数f1(x,y,z)对x、y、z分别进行求偏导运算，结果如式(11)～(13)所示：

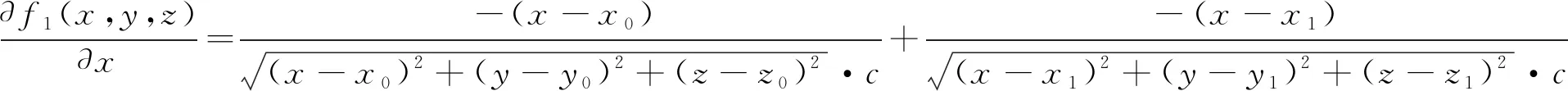
(11)

(12)

(13)

函数f2(x,y)对x、y、z分别进行求偏导运算，结果如式(14)～(16)所示：

(14)

(15)

(16)

函数f3(x,y,z)对x、y、z分别求偏导，结果如式(17)～(19)所示:

(17)

(18)

(19)

2 定位体制误差分析

衡量定位精度通常采用几何精度因子(GDOP)表示，通过分析GDOP定位误差分布，确定所采用定位体制有效的定位区域，并指导分析测量参数误差与定位精度的关联误差，方便指导工程应用。在该无源定位模型中，参数观测误差主要有时差测量误差精度dΔT、测向误差dβ、卫星的位置误差(dx0,dy0,dz0)、侦测站位置误差(dx1,dy1,dz1)，因此必须分析这些参数误差对定位误差的影响，确定本定位模型误差分布，则：

(20)

对观测方程中各式变形、求微分得到定位误差方程：

(21)

将式(21)表示成矩阵形式：

dV=CdX+dXs

(22)

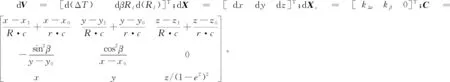
由式(21)整理之后得到：

dX=C-1(dV-dXs)

(23)

相应的误差协方差矩阵为：

(24)

由此，可以求得误差协方差矩阵PdX以及观测量(ΔT,β,Rl)对应的GDOP值：

EGDOP=[tr(PdX)]1/2=

(25)

3 定位仿真分析

在完成定位模型设计以及定位误差理论分析的基础上，通过设定不同的观测条件，做多次蒙特卡洛仿真试验，分别分析时差、测向、卫星轨道等测量误差条件下的目标GDOP误差分布曲线，并以此指导工程应用。由于侦收定位站为固定站，通过北斗或GPS系统可确定其位置，定位精度优于5 m，故定位站位置误差可忽略不计，因此重点分析时差、测向、卫星轨道误差等参数在不同测量精度条件下对本定位体制的GDOP误差分布曲线。

3.1 时差误差对定位精度影响

时差参数是定位方程中重要的观测量，因为时差信息中隐含目标与定位站、辐射源间的距离信息，该时差测量精度直接影响目标位置解算结果。因此在分析目标定位的几何定位精度时，要重点分析时差测量精度对定位结果误差的影响。目前按100 ns、200 ns 2种工程测量精度进行仿真试验，其仿真试验结果如图3 所示。从仿真试验结果可以看出：100 ns、200 ns 2种时差测量精度条件下，该种定位方法的绝对定位精度在20～50 m范围，可以确定时差测量精度对定位精度影响相对较小，这是由于地面站与卫星间形成了较长定位基线，能够实现高精度定位的技术条件。

图3 不同时差测量精度对定位精度影响试验

3.2 测向误差对定位精度影响

目标方向是定位方程中另外一个重要的观测量，该测量参数中包含目标与定位站的相对位置关系。故方向测量精度直接影响目标位置解算结果，因此需要重点分析目标方向测量精度对定位结果误差的影响。针对目前侦测系统的测向精度能力，按目前工程中约1°～2°的目标测向误差进行仿真试验分析，其仿真试验结果如图4 所示。从仿真试验结果可以看出：在1°测向误差条件下，600 km的定位区域内定位误差小于6 km(相对定位精度1%R)；在2°测向误差条件下，600 km的定位区域内定位误差小于12 km(相对定位精度2%R)。

图4 不同测向精度对定位精度影响试验

3.3 卫星轨道误差对定位精度影响

卫星位置是定位中的一个辅助参数，其位置精度在一定程度上影响定位结果。由于卫星的轨道信息可通过星历计算得到，但该位置信息与卫星实际的位置信息存在一定的误差，该误差会影响目标定位精度。因此分别考虑在1 km，10 km 2种轨道误差条件下进行仿真试验分析，其仿真试验结果如图5所示。从仿真试验结果可以看出：1 km，10 km 2种轨道误差条件下，定位误差均不超过100 m，可以证明卫星位置误差对定位精度影响相对较小。

图5 不同轨道误差对定位精度影响试验

3.4 系统定位误差仿真分析

对时差、测向、卫星轨道等定位参数设定不同误差进行了仿真试验，其仿真试验定位参数精度参考当前系统所能达到的技术能力和水平，结合蒙特卡洛仿真试验结果，对定位精度进行统计，其统计结果如表1所示。从仿真试验结果可确认本定位模型的有效性，且具有较高的定位精度。通过对定位模型仿真分析可知其定位精度主要受测向精度的影响，时差测量误差和卫星轨道误差对系统的定位精度影响较小，其引起的定位误差可忽略不计。

表1 系统定位精度统计

为实现远距离目标侦收，要求定位系统的散射侦收天线具有较高的波束增益，其测向精度通常会优于1°。该基于单站的测向时差定位模型能够实现600 km范围内1%R的定位精度，定位精度在无源定位跟踪体制中为较高技术指标，因此基于限定约束条件的单站测向时差定位方法能够实现目标高精度定位与跟踪。

4 结束语

本文研究了基于卫星外辐射源的单站定位方法，该算法主要针对目前所采用的二维测向时差定位系统复杂、设备成本高的问题，提出了一维测向时差定位模型，并将测量参数变化不明显的俯仰信息替换成地球表面方程，同时采用坐标系转换将测量参数进行统一，实现对目标位置的有效解算。通过仿真试验分析了时差、测向、卫星轨道不同测量误差条件下的目标GDOP误差，可以确认时差、卫星位置误差对该定位模型的定位精度影响较小，测向精度在当前的工程测向精度范围内时，本定位模型具有较高的定位精度，由此验证了该种定位模型的有效性和实用性，具有较强的工程推广价值。