基于阻抗矩阵法的阵列天线互耦效应分析

杨峥峥，宋文良

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

天线作为无线通信系统的信号发射或接收终端发挥着不可替代的作用，然而在实际应用中，单一的天线往往有方向性不强、增益不高等缺点。而将单一天线按照一定规律排列在一起的阵列天线则具有更窄的波束和更高增益的辐射性能[1]，传统上对阵列天线的分析是采用阵元在远区辐射场的叠加原理，然而当舰船上的空间有限时，必须考虑天线阵的小型化问题。当阵元之间的间距较小时，其互耦效应对于阵列天线的影响不容忽视[2-4]。

本文基于RWG基函数的矩量法对阵列天线的辐射进行分析[5-6]，采用RWG模型对天线表面进行剖分，使用边馈电模型法对天线加电，对单一天线与阵列天线的端阻抗、表面电流分布、方向图等特性进行分析对比；然后基于阻抗矩阵的思想，将阵列天线中所有阵元视做一个整体，并对其进行统一编号，使得阻抗矩阵中包含互耦信息；最后采用补偿矩阵的方式消除互耦影响，进行仿真验证。

1 单一天线的矩量法分析

采用矩量法分析阵列天线，本文所分析的均为偶极子天线，近似为非闭合结构，因此首先应建立起具有普遍应用性的电场积分方程，通过位函数理论,可以得到散射场与入射场之间的关系，如下所示：

(1)

式中：A(r)表示磁矢位；φ(r)表示电标位。

A(r)、φ(r)可分别表示为：

(2)

(3)

式中：J(r)表示目标表面的等效电流；G(R)表示均匀无界空间的格林函数。

将式(2)和式(3)代入到式(1)中，可以得到如下方程：

ES(r)=ηL(J)=-jkη·

(4)

式中：L表示由等效电流产生电场散射的算子。

由理想导体表面边界条件可知，导体表面上电场的切向分量为0，因此电场积分方程可以表示为：

(5)

为了准确模拟导体表面的电流分布，采用RWG基函数离散天线表面，RWG基函数模拟天线表面电流分布时，需要沿天线带轴向只有1个RWG边元，这样才能保证2个相邻RWG边元形成的电流矢量J指向带的轴向，天线带离散模型如图1所示。

图1 天线带离散模型

使用伽略金法，即权函数也选择RWG基函数对电场积分方程进行离散，则最终阻抗矩阵元素可以表示为：

(6)

式中：fm(r),fn(r′)表示RWG基函数。

本文考虑的是天线的辐射问题，因此激励应由天线本身产生，采取边馈电模型法对天线进行加电，如图2所示。

图2 馈电模型

天线的某个边元作为驱动边元，边元ln上的电压可以表示为：

(7)

在之后的仿真验证中，均假设馈电电压为1 V，即馈电电压为相位为0、强度为1的余弦函数。对于细带天线来说，在给定激励的前提下，由矩量法算出阻抗矩阵，再由Z·I=V就可以得到天线表面的电流分布。这里提到的阻抗矩阵，与传统意义上的电阻、电抗的概念有所不同，阻抗矩阵所表示的是导体表面剖分的RWG单元和单元之间的相互电磁作用。上述讨论的天线是单一的细带天线，单个天线的输入阻抗可以由下式表示

(8)

式中：Vn表示馈电电压；Jn表示流过馈电边的总电流。

单一天线采用矩量法计算后阻抗矩阵可以表示为：

式中：Zij(i=j)表示天线表面的RWG边元的自阻抗；而Zij(i≠j)则为天线表面的RWG边元的互阻抗，此时计算得到的阻抗矩阵为对角占优矩阵。

2 基于阻抗矩阵思想的阵列天线分析

当讨论对象为阵列天线时，一个不容忽视的问题就是阵列天线间的互耦效应，在阵列天线中，每一个天线元都可以等效为存在电磁耦合的开放电路，所以在发射信号时，单个天线元的表面电流不仅有馈电电流，还会有相邻阵元散射激励引起的电流，电流的变化又会引起输入阻抗的变化，因此阵列天线中的阵元端阻抗和单个天线中的阻抗有所不同。为了将互耦效应引入到矩量法计算阵列天线的过程中，可考虑一种广义的阻抗矩阵，即将阵列天线中的所有单元看成是一个整体，但式(8)仍然为各个分离单元的端阻抗表达式，对天线表面的RWG边元进行统一编号，这样Zij(i≠j)就不仅可以表示单个天线上RWG边元的相互作用，也将阵列中的其他阵元散射的作用考虑在内。广义阻抗分析时的阵列天线阻抗矩阵可以表示为：

若阵列天线中各个阵元表面被剖分程度与单个阵元一致，则N·K=M，K为阵元数目。互耦作为一种客观存在的现象，会严重影响阵列天线的性能，引起辐射方向图的失真和输入阻抗变化而导致的输入端口不匹配，因此在分析阵列天线的性能时必须将互耦因素考虑在内。传统的方向图综合中往往预先给出辐射特性，然后综合出阵列单元数、激励幅度和相位等。本文将方向图综合与矩量法相结合,使用切比雪夫综合法计算出相应的激励电流I0，然后将其与未考虑耦合效应时的阻抗矩阵Z0相乘,得到综合法中的激励电压V0，此激励电压即为矩量法中的激励电压，之后计算出带有互耦影响的阻抗矩阵ZMM，由此就可以在综合过程中考虑阵列天线间互耦效应的影响，算法流程如图3所示。

图3 算法流程

(9)

则补偿后的阵元上的电流分布可以表示为：

I=MZ-1V0

(10)

3 算法仿真分析

为了直观地观察阵列天线中互耦对端阻抗的影响，选择只有2个阵元的的阵列天线，因为2个阵元无论如何摆放，其相对位置是一致的，因此其端阻抗也是相同的。工作频率为75 MHz，阵元长度为2 m，随着阵元间隔的变化，其端阻抗化变化如图4、图5所示。

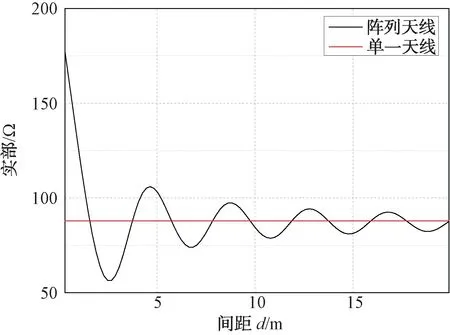
图4 端阻抗实部变化

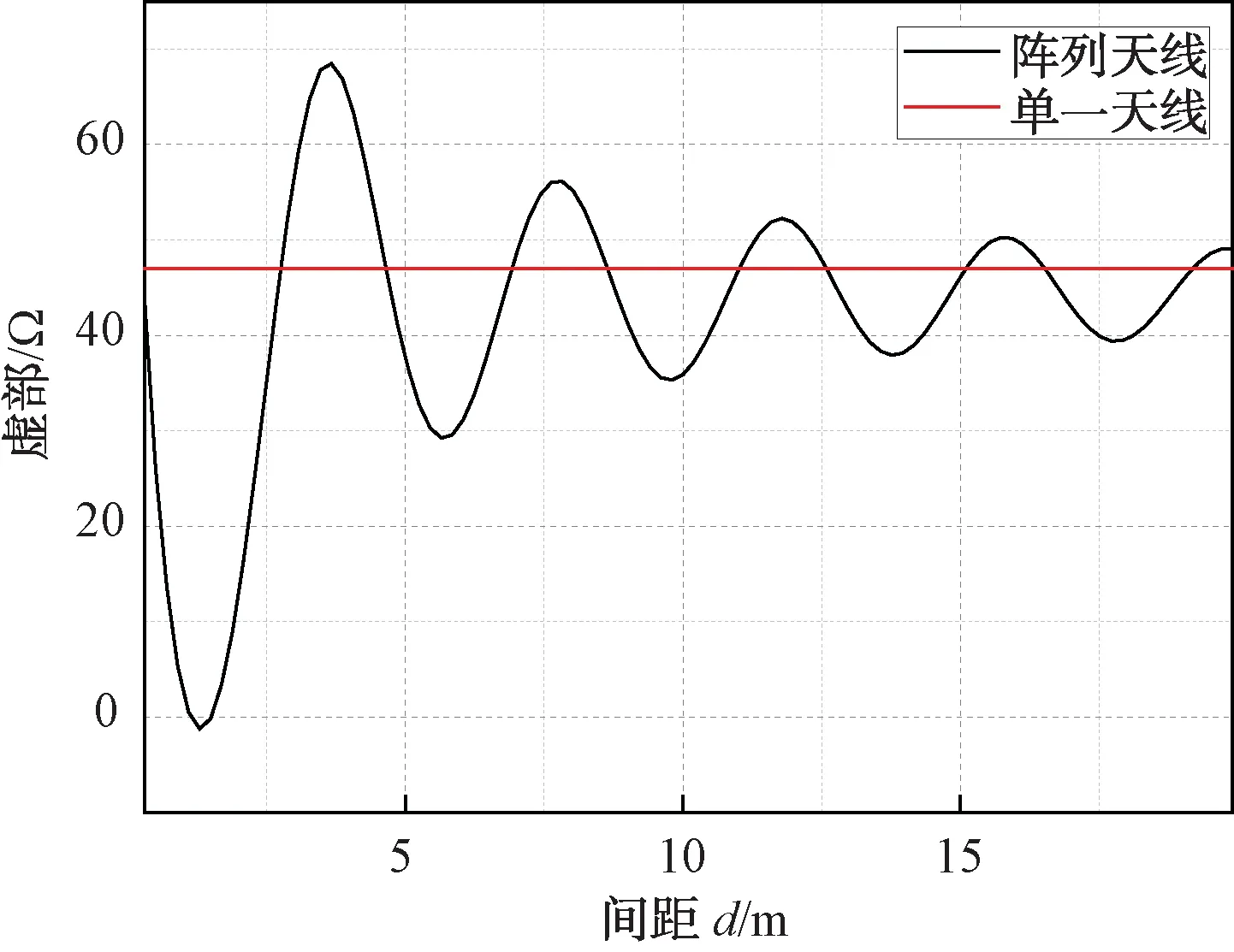
图5 端阻抗虚部变化

可以看出，随着阵元间距的增大，其端阻抗值也越来越趋近于单一天线的端阻抗值，也就是说阵元之间的距离越近，其互耦影响越大。阵列天线的一系列辐射特性实际上是源于其表面电流分布，由于二元阵列位置的相对一致性，无法从中很好地看出互耦对其表面电流分布的影响。考虑一个七元阵列，图6为七元偶极子天线阵列的表面电流可视化分布。

图6 天线阵列表面电流分布

阵元从左到右依次为位置1～7，对每个阵元中心点处的电流幅值进行提取可以得到表1。

表1 中心处电流幅值

由于阵列天线在结构上的对称性，因此其电磁环境也是对称分布的，可以看出，阵元的表面电流呈现对称分布，离阵元中心最远的位置1处和位置7处的电流幅值与中间阵元的误差最大，然而与中间阵元的误差并没有呈现线性变化，这种现象是阵元表面被划分的网格不够密集导致的。

接下来采用切比雪夫综合法，综合出副瓣电平为30 dB的十元阵列天线的激励电流，然后采用本文介绍的阻抗矩阵的思想计算出补偿矩阵，进而对互耦影响下的阵元表面的电流分布进行补偿，补偿前后的方向图如图7所示。

图7 补偿前后的方向图

可以看出互耦对于阵列天线的主瓣宽度影响不大，但是严重影响零点深度以及副瓣电平，而当采用了本文提出的互耦补偿方法后，补偿后的仿真曲线与理想情况下(无互耦)基本一致，验证了本文所提互耦补偿方法的正确性。

4 结束语

从单一天线的矩量法分析出发，推导出了单一天线矩量法分析的阻抗矩阵表达式，然后在此基础上使用阻抗矩阵的形式表征阵列天线间的互耦影响，提出了一种基于矩阵思想的互耦补偿方法，从矩量法的一般性流程探究，推导出了可以消除互耦影响的补偿矩阵，数值结果证明了本文方法的正确性和有效性。