基于代理模型与参数敏感性分析的扇形气膜孔优化

管俊俊， 张 祎， 张也平， 鲍阿美， 戴 韧

(1.上海理工大学 能源与动力工程学院，上海 200093；2.上海电气电站集团本部，上海 201199)

气膜孔的几何形状是影响气膜冷却效果的重要因素，为了改善冷却效果，研究人员提出了各种孔型。虽然冷却效率很高的孔型很多，但大部分孔型结构复杂，无法进行大规模工业加工，而扇形孔不仅冷却效率高，还具有结构简单、加工成本低等优点，是气膜孔优化研究中的重点[1-2]。

Gritsch等[3]研究发现，与圆柱孔相比，扇形孔能够增大气膜流向和侧向的覆盖面积，并在高吹风比下仍保持较高的冷却效率。扇形孔参数会影响其自身的冷却效果，包括倾斜角[4]、前倾角[5]、侧扩角[6]、长径比[7]和孔间距[8]等。其中，侧扩角和前倾角对扇形孔冷却效率的影响较大。

基于CFD数值方法对扇形孔几何形状进行优化的研究很多，包括多保真度模型[9]和深度学习预测模型[10]等，但目前成熟的方法仍是基于代理模型的优化方法[11-12]。此外，实验设计的优化方法也很多，包括拉丁超立方设计(LHD)[13]、均匀设计[14]和正交设计[15]等，但这些设计方法也存在不足，其生成的样本只能均匀分布在样本空间内。对于气膜冷却优化问题，不同变量对于目标的影响程度通常不同[16]。基于此，笔者提出两步法的扇形孔优化方法，对扇形孔的不同参数进行敏感性分析，确定目标的优化变量，以减少优化变量个数，保证代理模型的“凸”性，从而提高优化效率和收敛性。

1 优化方法

1.1 优化变量和目标函数

本文采用新的成型方法对扇形孔进行建模，成型过程见图1，其中S表示厚度。圆柱段形状由直径D、倾斜角α和圆柱段长度Lm确定。从A向视图可以看出，扩张段形状由出口前缘长度L1、尾缘长度L2和出口宽度H确定，具体过程是用样条曲线连接圆柱段出口和气膜孔出口，通过扫掠形成扩张段。参考文献[4]，设置倾斜角为35°，圆柱孔径为6 mm，横向孔间距为13D。优化变量为前缘长度L1、尾缘长度L2、出口宽度H和圆柱段长度Lm，其余参数保持不变。优化变量的取值范围见表1。

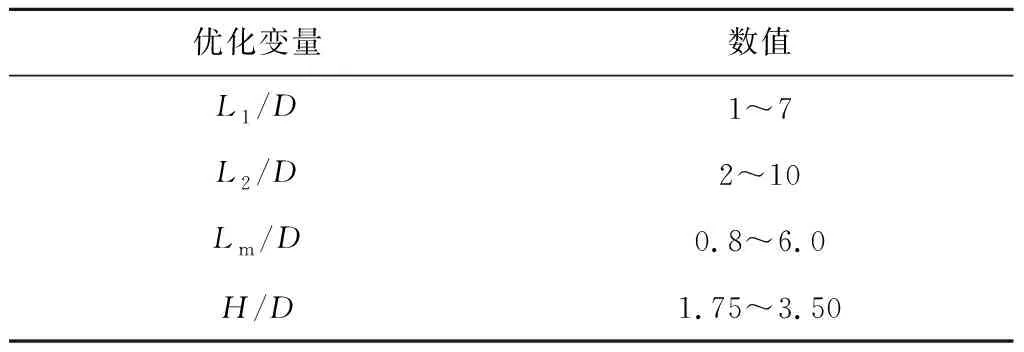
表1 优化变量范围Tab.1 Range of optimization variables

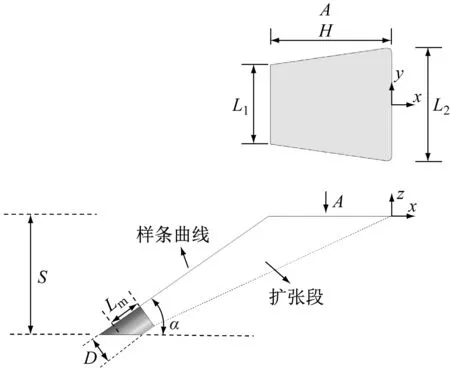
图1 扇形孔成型过程示意图Fig.1 Schematic diagram of fan-shaped hole forming process

(1)

式中：ηLat为横向平均冷却效率。

(2)

(3)

式中：η为绝热冷却效率；T∞、Tc和Taw分别为主流温度、冷气温度和绝热壁温。

1.2 敏感性分析

在敏感性分析过程中，选择主效应和贡献率作为比较优化变量对目标函数敏感性大小的标准。其中，主效应表示因子在某个水平时所有响应的平均值，贡献率表示因子对响应影响程度的百分比，按因子对响应的贡献排列可得到Pareto图。

1.3 Kriging代理模型及遗传算法

Kriging代理模型(KSM)[13]是一种利用随机变量估计非设计点上数值的统计方法。未知函数y(x)的近似表达式为：

y(x)=f(x)+z(x)

(4)

式中：f(x)为用常数项表示的全局函数；z(x)为均值为0、带有协方差的高斯过程函数。

识别2个或多个随机变量相关性的z(x)的协方差可以用总体方差σ2、相关矩阵R以及相关函数R(xi,xj)来表示。

Cov(xi,xj)=σ2R[R(xi,xj)]

(5)

(6)

式中：m为训练样本个数;θk为相关参数;xi、xj均为相关变量。

如果确定相关函数，可得到：

(7)

(8)

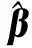
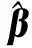
(9)

(10)

θk≥0(k=1,2,…,m)

由θ构成的Kriging代理模型为拟合精度最优的代理模型。

多岛遗传算法(Multi-island GA)通过模仿生物进化过程中的遗传繁殖机制，对优化问题解空间的个体进行编码,然后对编码后的个体种群进行遗传操作，通过迭代从新种群里寻找含有最优解的组合。流程如下：(1)初始化种群；(2)计算种群中每个个体的适应度；(3)按由个体种群适应度所决定的规则选择进入下一代的个体；(4)按交叉概率Pc进行交叉操作；(5)按变异概率Pm进行突变操作；(6)如果没有满足停止条件，转到步骤(2)，否则转到步骤(7)；(7)输出种群里适应度最优的染色体作为问题的满意解或最优解。

1.4 优化流程

图2为优化流程示意图。根据表1中的优化变量范围，利用LHD方法生成样本，基于计算流体动力学(CFD)数值方法确定目标函数集，通过Kriging代理模型建立气膜冷却的预测模型，采用多岛遗传算法寻优，寻优过程中子群数量为10个，岛的数量为10个，迭代过程为10代。

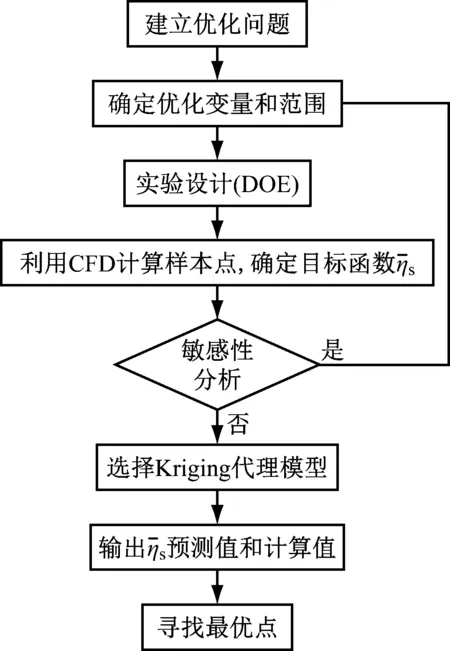
图2 优化流程示意图Fig.2 Optimization process diagram

为比较基于敏感性分析的优化效果，进行两组优化。第1组优化一次性生成22个样本，不进行敏感性分析，使用Kriging代理模型进行优化,即一步法，优化孔命名为优化孔A。第2组先生成11个样本，进行敏感性分析，缩小样本空间后再生成11个样本，总共22个样本，使用Kriging代理模型进行优化,即两步法,优化孔命名为优化孔B。

2 CFD数值方法

2.1 计算域和边界条件

图3给出了模型的几何尺寸，该模型由主流通道、气膜孔通道和供气室组成。主流通道长、宽、高分别为170D、13D和17D，供气室长宽高分别10D、13D和12D。

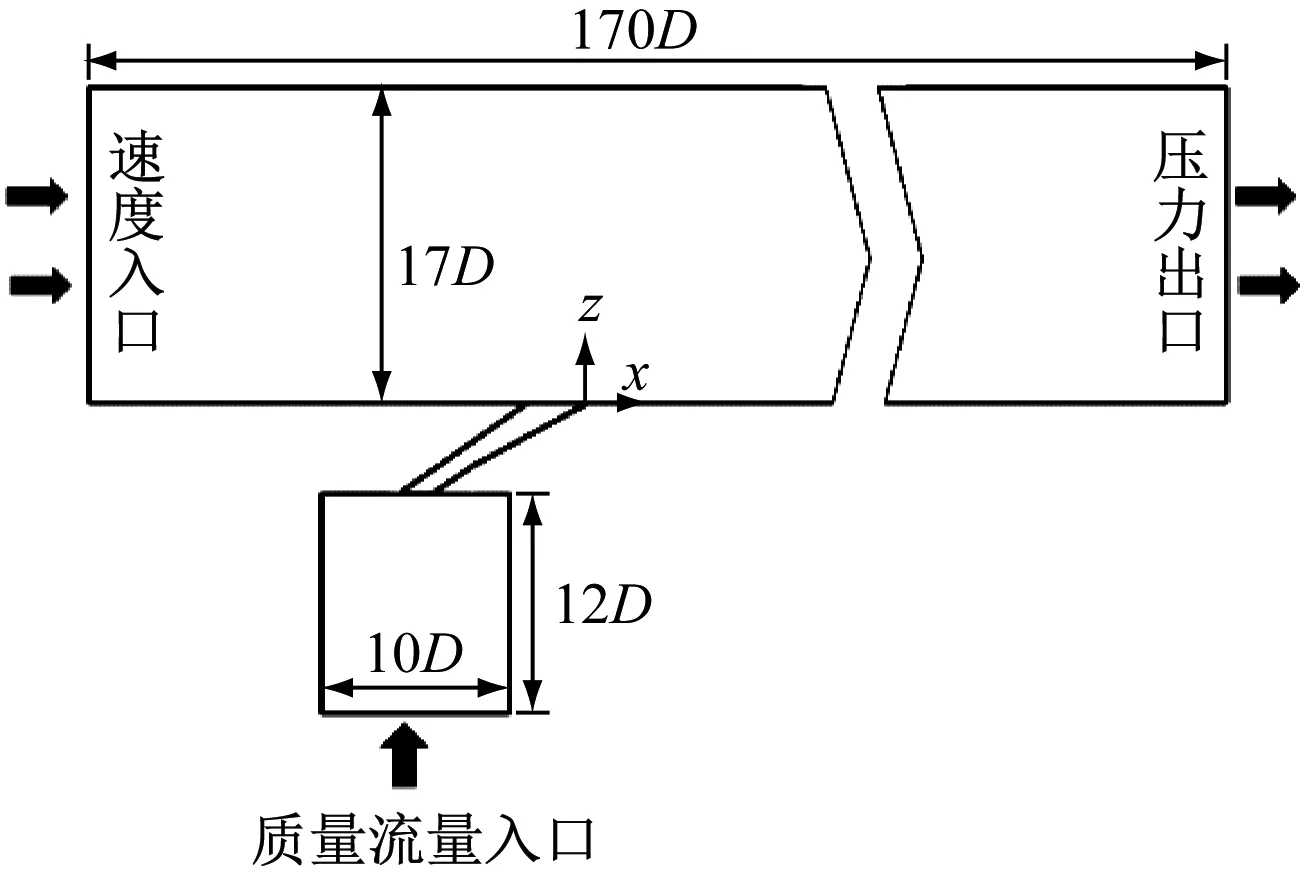
图3 计算模型及边界条件Fig.3 Calculation model and boundary conditions

主流采用速度入口和压力出口，主流通道两侧为周期性边界条件，冷气入口为质量流量入口，其余边界为绝热无滑移壁面，通过改变冷气质量流量qm,c来调整吹风比M。

(11)

式中：ρ∞、ρc分别为主流和冷气密度；U∞为主流入口速度；Ac为气膜孔圆柱段的截面积;Uc为气膜孔圆柱段截面的面平均速度。

主流入口速度U∞为20 m/s，主流温度T∞为317.35 K，冷气温度Tc为299.25 K，主流和冷气入口湍流度均为1%。选择Ansys Fluent为数值模拟的求解器，湍流模型选用Realisablek-ε模型。

吹风比对气膜优化结果有一定影响[17]。一般吹风比范围为0.5～2.5，本文取1.5，仅进行单工况优化，将其他吹风比的冷却效果作为后续检验。

2.2 网格无关性验证和数值验证

选择Pointwise17.3作为网格划分软件。图4给出了模型网格拓扑结构，孔出口和气膜覆盖区域由大密度六面体网格填充，气膜孔通道由四面体网格填充，其余部分由三棱柱网格填充。采用3套网格对气膜横向平均冷却效率进行无关性验证，网格数分别为140万、310万和480万，见图5。网格数分别为310万和480万时，横向平均冷却效率变化不大，因此选择网格数为310万，第1层网格高度为0.01 mm，拉伸比为1.1，y+<1。

图4 模型网格拓扑结构Fig.4 Topology structure of model grid

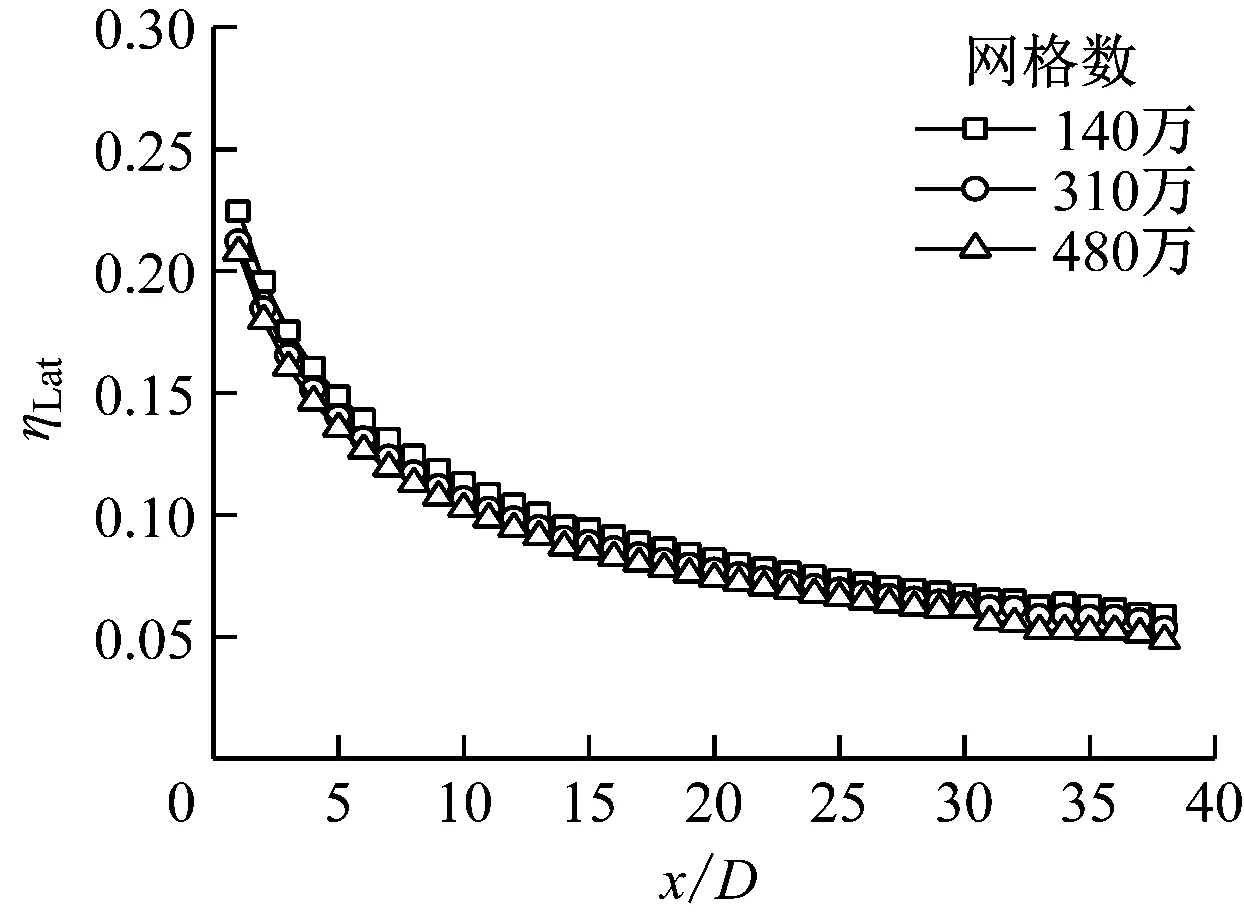
图5 网格无关性验证Fig.5 Grid independence verification

为验证CFD数值方法的准确性，选择扇形孔作为验证模型，并与文献[4]中的实验结果进行对比。图6给出了M=1.5时横向平均冷却效率计算值与实验值的对比结果。从图6可以看出，基于Realisablek-ε模型的横向平均冷却效率计算值与实验值更接近，因此选择Realisablek-ε作为计算模型。

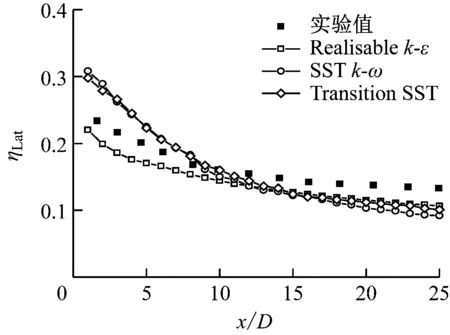
图6 横向平均冷却效率计算值与实验值的对比

3 结果与分析

3.1 敏感性分析结果

表2给出了两步法第1轮样本计算结果。图7为通过对优化变量的敏感性进行分析得到的Pareto图。从图7可以看出，Lm对目标的贡献率最大，说明Lm发生变化会对面平均冷却效率造成较大影响；L1和L2的贡献率次之，H的贡献率最小，敏感度也最小，其对面平均冷却效率的影响很有限。

表2 两步法第1轮样本计算结果

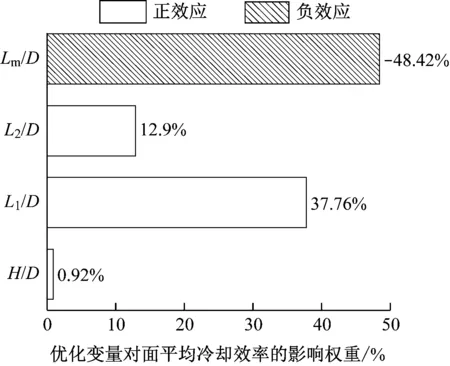
图7 Pareto图Fig.7 Pareto diagram

从图7可以看出，Lm对面平均冷却效率产生的是负效应，面平均冷却效率随Lm的增大而减小；而L1、L2和H对面平均冷却效率产生的是正效应，增大其数值有利于提高面平均冷却效率。

为便于比较，采用式(12)对各优化变量进行无量纲化，其中X表示各变量，Xmax、Xmin分别为变量上下限，Xi为第i个变量取值。

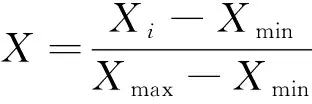
(12)

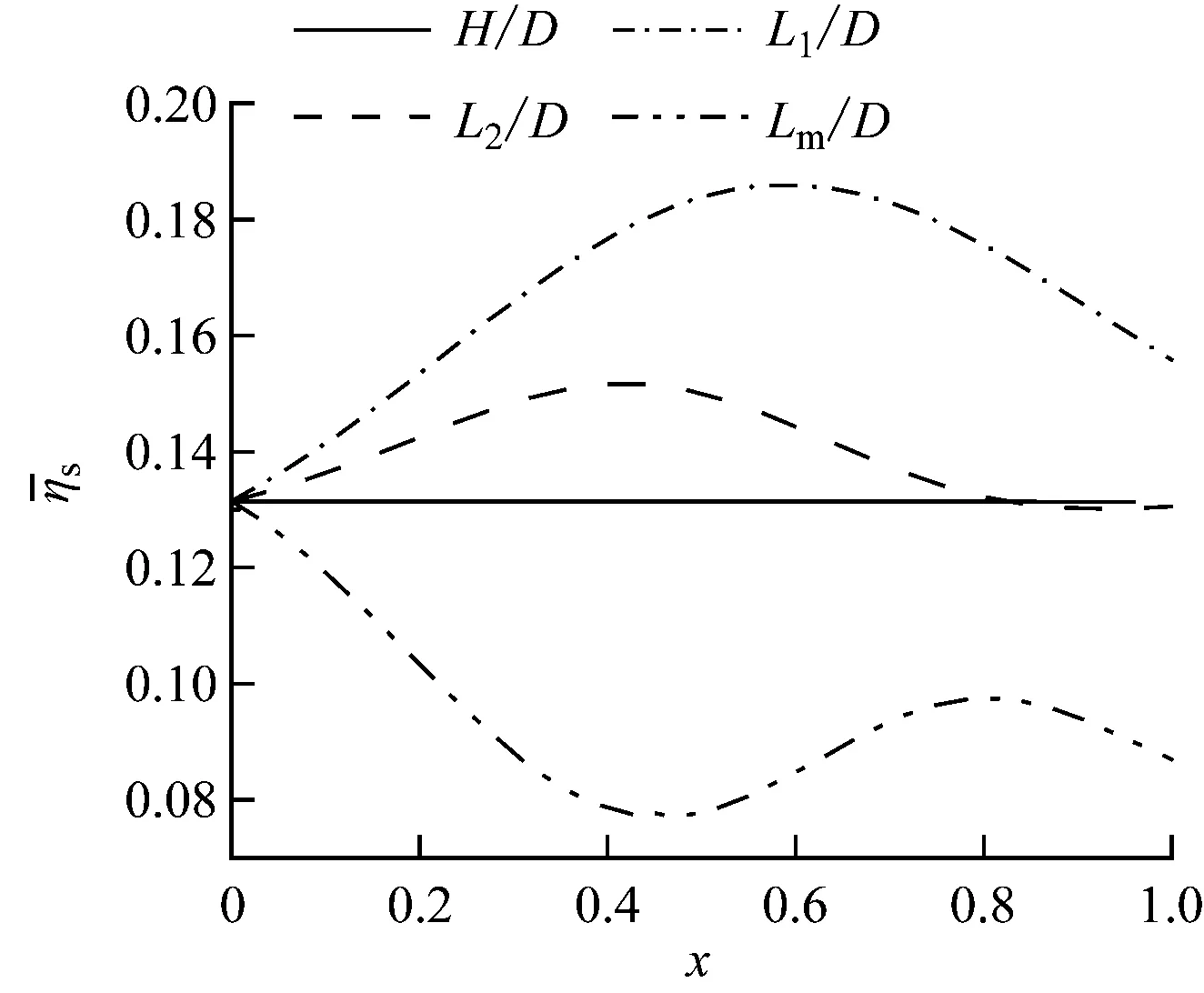
图8 优化变量对目标函数的影响Fig.8 Influence of optimization variables on the objective function

综上，Lm、L1和L2的敏感度较大，因此重新确定这3个优化变量的取值范围来生成第2轮样本，找出不同优化变量对应面平均冷却效率较高的区域，以该区域作为第2轮优化变量的取值范围。具体过程可表示为：

(13)

其中CX是常数，表示优化变量X对应的面平均冷却效率下限，该下限需要人为确定。第2轮样本各优化变量的取值范围见表3，基于LHD生成的两步法第2轮样本计算结果见表4。

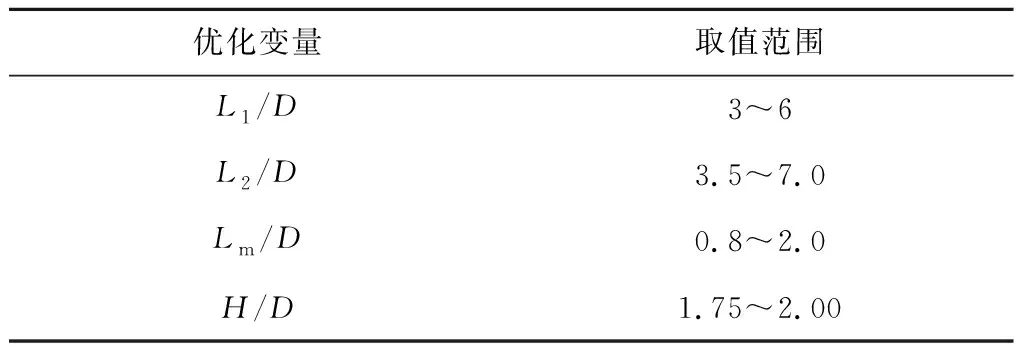
表3 敏感性分析后优化变量的取值范围

表4 两步法第2轮样本计算结果

3.2 优化结果对比

表5给出了M=1.5时原型孔和优化孔的优化变量和面平均冷却效率的预测结果。2种优化孔的面平均冷却效率均大于原型孔。其中，优化孔B的面平均冷却效率计算值较优化孔A更大，且预测误差更小。这说明基于敏感性分析的优化结果精度更高，预测效果更好。

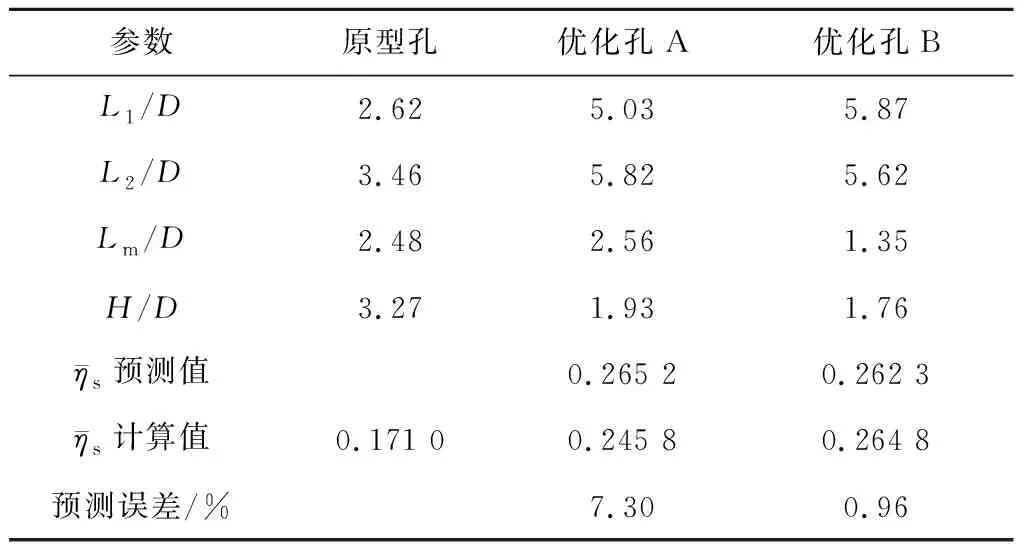
表5 原型孔和优化孔的几何参数及预测结果对比

如图9所示,从气膜的覆盖范围看，寻优方向主要是拓展气膜侧向宽度，即L1和L2的长度，气膜侧向宽度增大，气膜覆盖面积增大。如图10所示，优化孔B的气膜侧向覆盖范围大于优化孔A的气膜侧向覆盖范围，其更能体现L1和L2对目标的敏感度，因此冷却效果更好。

(a) 原型孔

(b) 优化孔A

(c) 优化孔B图9 M=1.5时气膜有效度的对比Fig.9 Comparison of film effectiveness at M=1.5

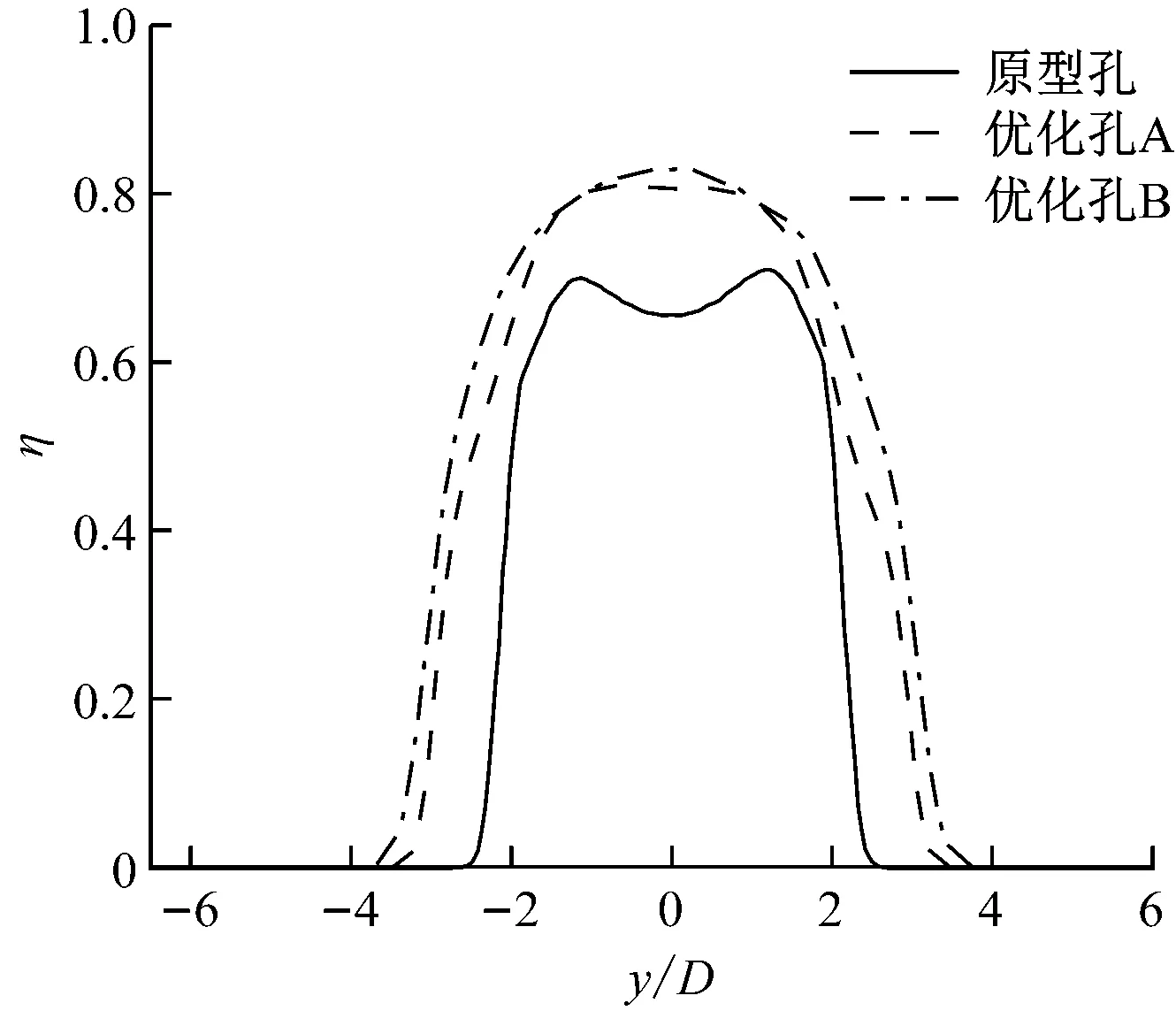
图10 M=1.5时距离孔出口尾缘2D处绝热冷却效率的对比

图11给出了吹风比为1.5时3种孔型横向平均冷却效率的对比。与原型孔相比，2种优化孔均能够提高横向平均冷却效率，其中优化孔B的横向平均冷却效率更高，说明基于敏感性分析的优化方法能够提高优化精度，优化效果更好。

图11 M=1.5时不同孔型横向平均冷却效率的对比

3.3 吹风比的影响

图12给出了吹风比对不同孔型气膜有效度的影响。从图12可以看出，2种优化孔的气膜有效度分布具有2个相似的特点。第一，在相同吹风比下，相比原型孔，2种优化孔在气膜孔出口区域的绝热冷却效率有较大提升，沿着流向气膜能延伸到下游更远的区域；优化孔A和优化孔B均沿横向增大了气膜覆盖面积，使得冷气能在更大范围内铺展开，从而提升了冷却效果。第二，当吹风比增大时，原型孔的冷却效果提升不明显，其绝热冷却效率和气膜覆盖面积变化不大，在M=2.5时原型孔气膜有效度分布甚至会出现分叉现象，冷却效果降低；优化孔A和优化孔B的绝热冷却效率和气膜覆盖面积均随吹风比的增大而增大，在大吹风比下绝热冷却效果最好。与优化孔A相比，优化孔B的气膜沿横向能够拓宽更大的距离，在相同吹风比下其气膜覆盖面积更大，随着吹风比的增大,这种差异会逐渐体现出来。

(a) 原型孔、M=0.5

(d) 原型孔、M=1.0

(g) 原型孔、M=1.5

(j) 原型孔、M=2.0

(m) 原型孔、M=2.5

图13给出了不同孔型面平均冷却效率的对比。在M=2.0时原型孔存在最大面平均冷却效率，而优化孔B的面平均冷却效率随吹风比的增大而提高，在M=2.5时面平均冷却效率最大。虽然优化孔A和优化孔B的面平均冷却效率的变化趋势相似，但在相同吹风比下优化孔B的面平均冷却效率更高，尤其在M=2.5时，优化孔B的面平均冷却效率比优化孔A高出0.03。因此，基于敏感性分析的优化方法不仅精度高，其预测结果也更准确。

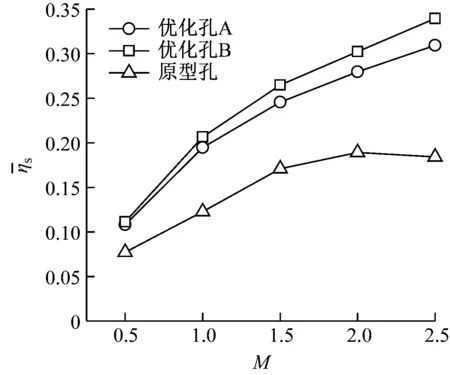
图13 不同孔型面平均冷却效率的对比

4 结 论

(1) 气膜孔结构参数对冷却效果的影响存在差异，其中扇形孔出口前缘长度L1、尾缘长度L2和圆柱段长度Lm对面平均冷却效率的影响较大，敏感度较强，而出口宽度H的影响最小，敏感度最弱；Lm对面平均冷却效率产生的是负效应，而L1、L2和H对面平均冷却效率产生的是正效应。

(2) 经过敏感性分析后的样本分布更加合理，代理模型的预测精度和寻优计算的收敛性均得到提高，结果均优于无敏感性分析。