压痕法评价奥氏体不锈钢拉伸性能的神经网络分析

孙明成，李英治

(1.辽宁省电力有限公司 电力科学研究院，沈阳 110006；2.辽宁东科电力有限公司，沈阳 110179；3.挪威船级社,荷兰阿纳姆 6812)

0 引言

材料力学性能的获取通常需要对标准试样进行测试，并对试样的尺寸和数量有一定的要求。然而，在对成品设备进行材料力学性能测试时，一般不能进行破坏取样[1-2]。仪器化压入法是在传统的布氏硬度和维氏硬度试验基础上发展起来的新的材料力学性能测试技术[3-4]。该方法通过同步测试和记录压头压入试样过程中的载荷-位移曲线，提供比传统硬度试验更丰富的信息，除硬度外，还可以获得材料其他的基本力学性能，如弹性模量、屈服强度和抗拉强度等。压入法的优点包括：设备小巧便携，能直接在现场进行力学性能测试；不需要进行破坏取样，能对在役设备进行测试；测试部位微小，可以用于材料局部特性的测定。目前，该方法已应用于许多工程场合中，例如对石油管道、核反应堆压力容器、电站设备等的安全评定。

目前已经发展了几种确定力学性能的分析方法，其中最受关注的是表征应力应变法、量纲分析法、神经网络法和有限元法。ISO/TR 29381—2008标准总结了过去20年的成就，介绍了由球压痕试验确定材料力学性能的3种分析方法：表征应力应变法、有限元法和神经网络法。神经网络方法已被广泛应用于模式识别、人工智能、控制工程、优化和信号处理等领域，还被用于处理压痕蠕变问题[5-10]。该方法同样可以适用于处理球压痕曲线来获得奥氏体不锈钢的屈服强度、抗拉强度、弹性模量和布氏硬度等力学性能，以下在此方面进行有关探索。

1 奥氏体不锈钢的特性及经验模型

1.1 Hollomon模型

加工硬化曲线显示出金属材料在一定的组织和变形条件下，宏观应力随应变的变化规律。一般通过单轴拉伸试验进行测量，并用数学模型来表征。当塑性变形足够大时，采用Hollomon提出的经验公式σ=Kεn(其中σ为真应力，K为应变硬化常数，ε为真应变，n为应变硬化指数)。

Hollomon模型能够描述常见工程材料的加工硬化行为。在双对数图上绘制应力-应变数据，并在较高应变水平下，用拟合线来评估这些参数。由直线的斜率给出n值，ε=1处的截距给出K值。在理想情况下，这两个参数应完全描述真应力-应变曲线的形状。K值表示材料的强度水平和成形过程中所需的力大小，而n值与真应力-应变曲线的斜率相关，表征材料延缓变形局部化能力。

然而，许多材料在低应变下并不严格遵循Holloman模型[11]。在低碳钢、锆合金、铜和316不锈钢中曾报道过双n行为。304不锈钢的单轴拉伸曲线如图1所示。在低应变阶段，304不锈钢在双对数坐标系中的加工硬化曲线具有明显的上翘行为，如图2所示，许多材料也表现出类似的行为。

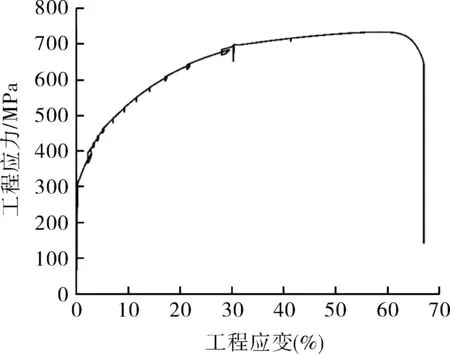
图1 304不锈钢的单轴拉伸曲线Fig.1 Uniaxial tensile curve of 304 stainless steel

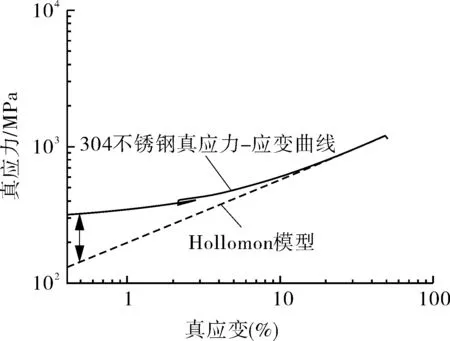
图2 304不锈钢在双对数坐标中的应力-应变曲线Fig.2 Stress-strain curve of 304 stainless steel in the double logarithmic coordinate system

1.2 Ludwik模型

Hollomon模型未能很好地模拟奥氏体不锈钢的特性，因此人们提出了另外几种描述该类钢性能的模型[12-13]。

Ludwigson提出了修正的关系式，解释了低应变下的偏差是低层错能材料的特征，这是由于低应变下的平面滑移和高应变下的交叉滑移不同造成的。

Ludwigson模型方程：

σ=Kεn+exp(K1+n1ε)

(1)

Ludwik则用另一种方程模型来描述应力应变数据[14]：

σ=σy+Kεn

(2)

这些经验模型能够描述奥氏体不锈钢材料双对数坐标系中的上翘行为。本文选择Ludwik模型，该模型能模拟奥氏体不锈钢的单轴应力-应变曲线，而且仅需3个参数；而Ludwigson模型需要4个参数，这使得神经网络数据库变得更为复杂。

2 神经网络法求解球形压痕曲线

神经网络法基于Ludwik模型进行有限元仿真，建立数据库。用随机选择的一对材料参数输入和压痕曲线输出向量对神经网络进行训练。通过训练过程，神经网络能够学习输入和输出数据之间的近似关系，然后通过优化程序找到材料参数，使试验观测值与神经网络模拟预测值之间的误差最小。这种方法的最大优点是不再需要有限元模拟，因为所有的知识信息都包含在神经网络中，也包括了材料在压入过程中的凸起/凹陷效应[15]。与有限元的逆向求解相似，神经网络的逆向求解也不可避免地遇到了唯一性的问题。由于锥形压头的自相似性，应变与压痕深度无关，所以锥形压痕的逆向求解不存在唯一性。进一步研究表明，为了确保唯一性，需要采用不同锥角的两次压痕确定材料参数。采用球形压头避免了锥形压头的自相似性，压入过程中接触半径非线性变化，从而改善了逆向求解的唯一性和敏感性。本文采用球形压头建立神经网络；此外，在优化求解中，采用Matlab工具箱中全局最优化的算法，采用40个不同的初值点搜索全局最优解。

2.1 有限元模型

为了建立神经网络数据库，采用有限元软件进行仿真计算。在本文的有限元模拟中采用了二维轴对称8节点单元183，有中间节点。单元数量为1 540个，节点数为4 592个。球型压头和试验材料之间使用刚性接触单元。在压头和试验材料接触区域采用加密网格。最小单元尺寸为0.002 5 mm。为了检查有限元模型的正确性，使用了4种网格进行计算并比较所得结果的误差。这些网格的最小单元尺寸分别为0.005,0.003 3,0.002 5,0.002 mm。计算的前提条件是材料的屈服强度为300 MPa，幂硬化指数为0.5，弹性模量为1.9×105MPa,压痕深度为150 μm。计算结果表明，相应的最大载荷分别为466.81，465.17，463.02,461.73 N。从最小单元尺寸0.002 5 mm加密到最小单元尺寸0.002 mm，最大载荷相差仅为0.28%。因此确认最小单元尺寸为0.002 5 mm的网格划分比较合适。在确定有限元网格的正确性之后，进行神经元数据库的建立和分析计算，并将神经网络法测试结果与单轴拉伸试验结果进行了对比，两者吻合较好。

摩擦系数与压头材料有关。金刚石压头摩擦系数在0.1～0.15之间，碳化钨压头的摩擦系数在0.4～0.6之间。采用了6种不同的摩擦系数计算最大的载荷值。摩擦系数为0.15～0.45，所得的最大载荷值在450.83～463.92 N之间，相差不到2.8%。在本次的模拟中，摩擦系数采用了制造商给出的碳化钨压头摩擦系数的数值0.35。网格划分如图3所示。

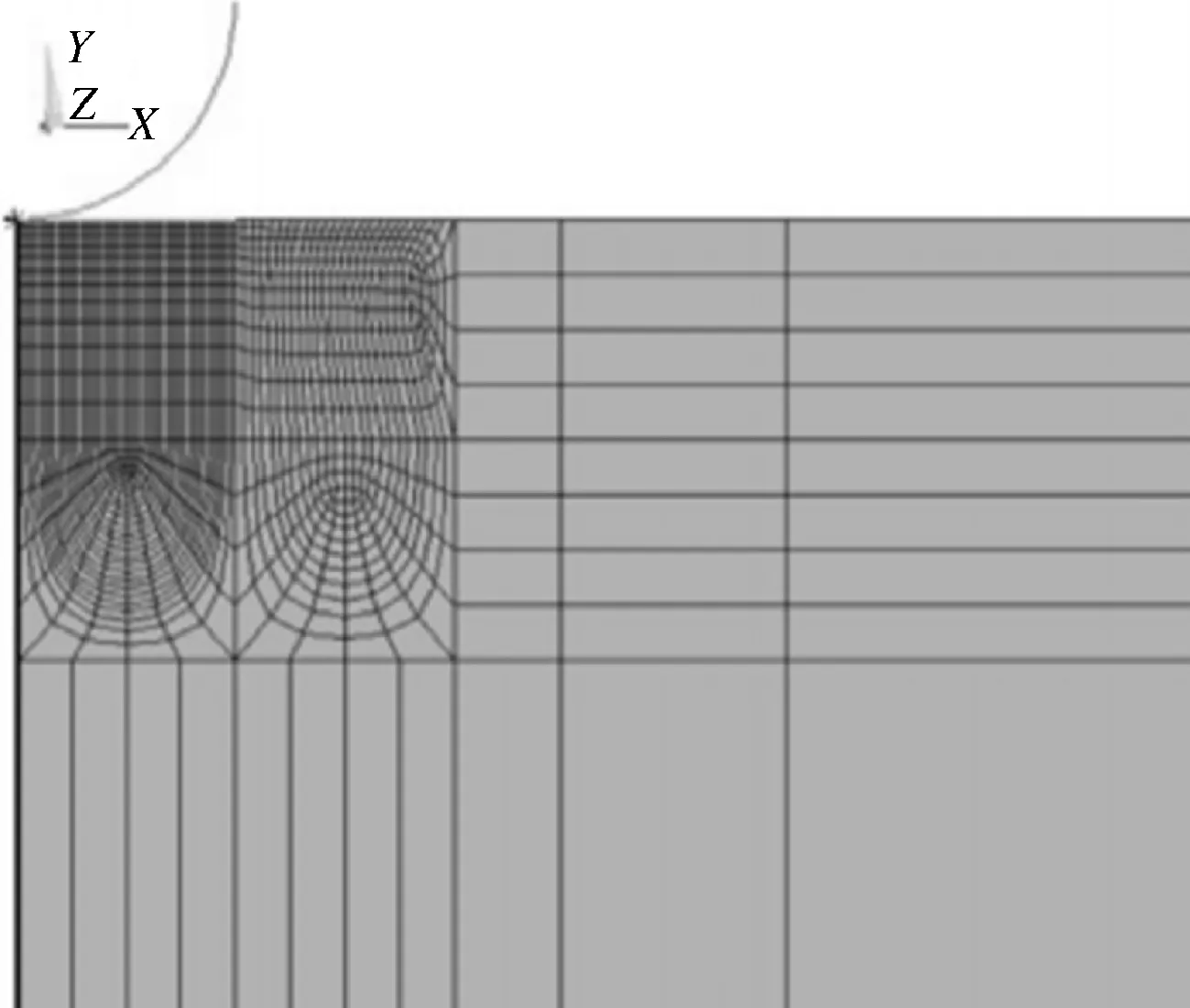
图3 有限元模拟的网格划分Fig.3 Mesh division in the finite element simulation

2.2 数据库结构

多循环压痕曲线是指加载到一定深度，部分卸载，然后继续加载到更大的深度，再部分卸载，如此不断重复直至得到所需要的多循环压痕曲线。在数据库中，共有11种不同类型的多循环曲线，可以用来训练神经网络。这些曲线的最大深度从80～180 μm，加载过程中，深度以10 μm的间隔均匀增加，在卸载过程中，深度以5 μm的间隔减少(见图4)。

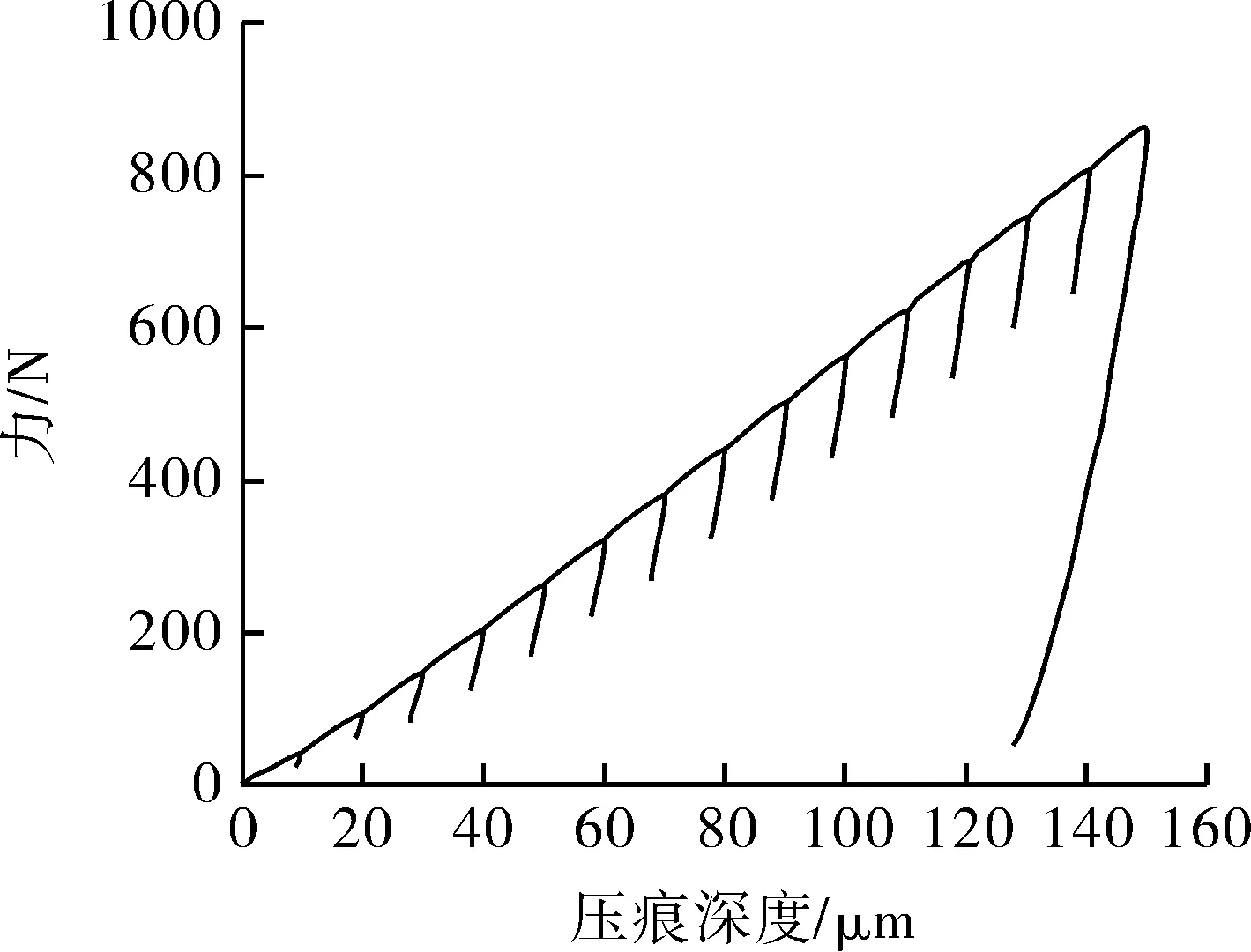
图4 数据库中304不锈钢多循环压痕曲线Fig.4 Multi-cycle indentation curve of 304 stainless steel in the database

使用不同材料参数建立有限元分析数据库。对于一个给定的材料参数pi，需要模拟得到载荷-位移曲线F(u,pi)和残余压痕直径，此外还需要包括压入过程中的凸起/凹陷的影响。相关的数据被储存到数据库中，用来训练神经网络。数据库结构如表1所示。

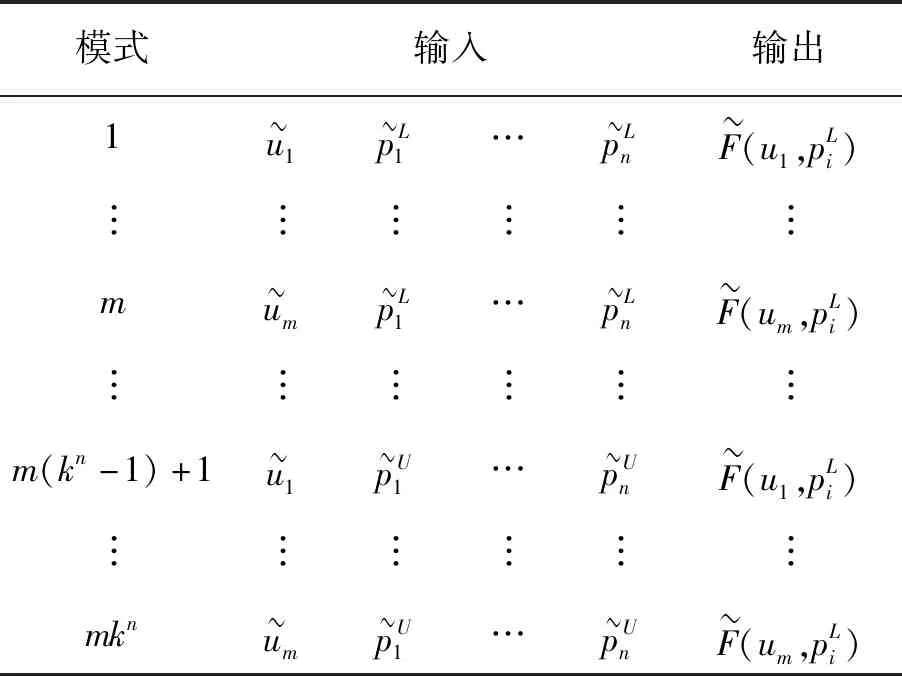
表1 数据库的结构Tab.1 Structure of database

注：u1,…,um为m个离散深度值，pi,…,pn为n个材料参数的集合;表中的每一行表示一个训练模式，F(u,pi)是相应模式的载荷。

采用以下公式对压痕深度、载荷和材料参数归一化处理。

(3)

(4)

(5)

式中，L为下限值；U为上限值；in为输入数据的标准化；out为输出数据的标准化。

对于深度u,力F,输入in和输出out的上限和下限值见表2。

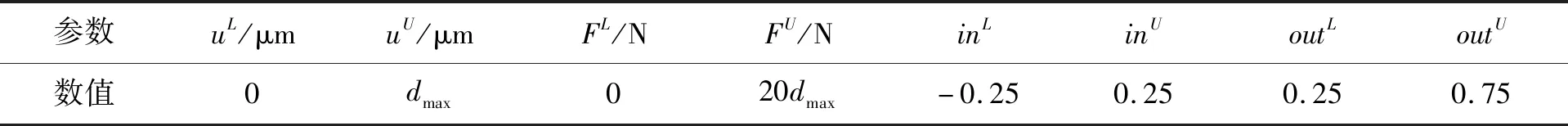
表2 深度u,力F,输入in和输出out的上限和下限值Tab.2 Lower bound and upper bound for u,F,in and out

2.3 创建神经网络

在Matlab中，图5示出一个具有S个神经元和R个输入参数的典型神经网络层。其中P是维数为R×1的输入(或参数)矩阵，W是维数为S×R的权重矩阵，b是维数为S×1的偏差矩阵。偏差b与向量积W×P之和为n，传递给传递函数f得到神经元的输出a，即维数为S×1的输出矩阵(或目标矩阵)。

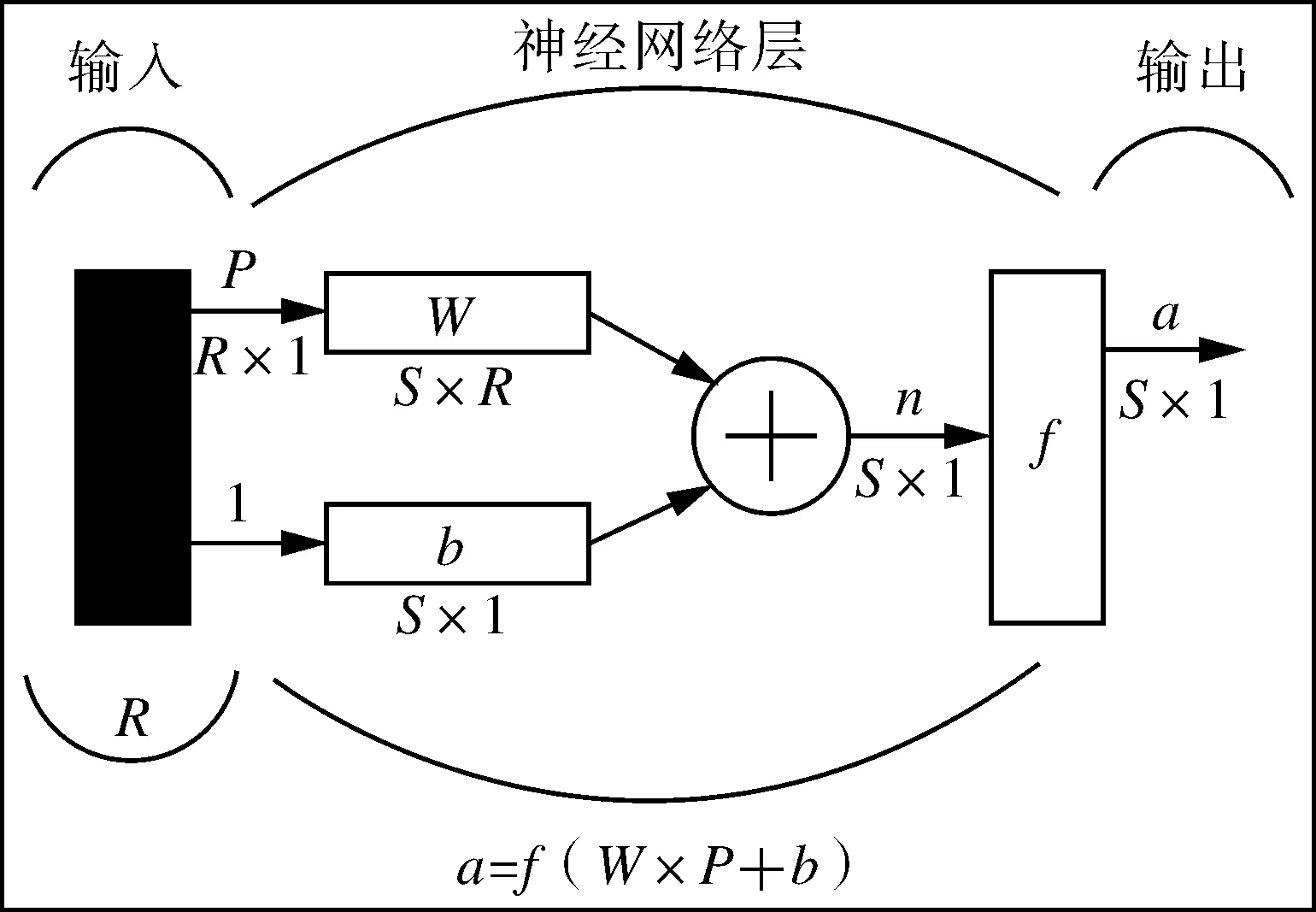
图5 神经网络创建Fig.5 Establishment of neural network

a=f(W×P+b)

(6)

Matlab提供了newff函数来创建反向传播网络。例如，用P作为参数矩阵，T作为目标矩阵，创建一个由20个神经元组成的单层网络：

net=newff(P,T,20)

(7)

为了处理多循环压痕曲线，需要将整个曲线分为两部分，即加载部分和卸载部分。此外，为了确定表征应力应变和布氏硬度，还需要接触深度和接触半径的信息。因此，创建了3个网络net0,net1和net2。

net0=newff(P0,T0,20)

(8)

net1=newff(P1,T1,20)

(9)

net2=newff(P2,T2,20)

(10)

式中,参数矩阵P0,P1为输入矩阵。在表1中，归一化u表示加载部分的位移P0和卸载部分的位移P1；pi表示材料参数(σy,n,K)；目标矩阵T0和T1是输出，归一化F(u,pi)表示加载部分载荷T0和卸载部分的载荷T1。

参数矩阵P2也为输入矩阵。由于残余半径仅和每次卸载相关，归一化的u代表卸载开始点的深度。目标矩阵T2是归一化接触半径a(u,pi)的输出：

(11)

其中，aL=0,aU=R(R为压痕半径)。

2.4 神经网络训练

与生物神经网络一样，人工神经网络也需要通过训练获得智能。实际上，人工神经网络训练过程的目的是调整式(4)中的权重矩阵W和偏差矩阵b[16]。在Matlab中，利用Levenberg-Marquardt算法(函数lmtrain)实现了调整权重矩阵W和偏差矩阵b的求解。具体是将训练样本分成3部分，60%用于确定W矩阵和b矩阵；20%用于测试其准确性;20%用于验证有效性。用参数矩阵P和目标矩阵T训练网络的语法，以及训练样本的划分，可以表示如下：

[neti,tr]=train(neti,Pi,Ti)

(12)

net.divideParam.trainRatio=60%

net.divideParam.testRatio=20%

net.divideParam.valRatio=20%

神经网络的训练相当耗时，因此编写了Matlab函数，预先训练网络，并将结果存储在Matlab.m文件中。当调用Matlab函数sim进行仿真时，读取Matlab.m文件，提供训练后的数据。

2.5 神经网络模拟

神经网络经过训练后具有智能性，可以用于仿真模拟。Matlab仿真模拟函数为sim，公式为：

outputi=sim(neti,inputi)

(13)

2.6 材料参数识别及流程图

材料参数的识别过程与有限元逆向方法类似。不同之处在于，输出载荷-位移曲线和残余接触半径是通过神经网络模拟而不是通过有限元计算获得的。材料参数识别流程如图6所示。

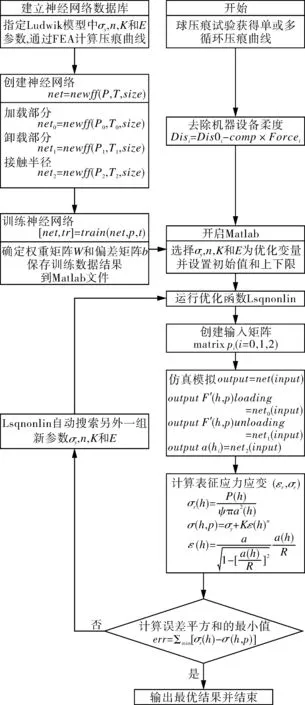
图6 神经网络训练方法的流程Fig.6 Flow chart for neural network training method

设p表示材料参数。需要优化的参数为σy,n,K，它们可以作为神经网络模拟的输入，输出的是载荷-位移曲线和残余接触半径。通过求解方程使试验值和计算值的误差平方和最小，从而确定材料参数。真实的材料参数将产生与试验曲线最接近的匹配。误差为试验的载荷-位移曲线F(h)和计算的载荷-位移曲线F′(h,p)之间的差值。该过程通过最小化函数实现：

err=∑min[F(h)-F′(h,p)]

(14)

计算中采用了Matlab优化工具箱中的非线性最小二乘优化函数lsqnonlin。优化过程通过梯度求值逐步迭代直到收敛。

以Ludwik模型中的参数σy,n,K和弹性模量E为优化参数，建立本构方程。作者发现载荷-位移曲线收敛后，从载荷-位移曲线导出的表征应力应变(εr,σr)仍然不符合本构方程。因此提出了一种双重判据：既考虑载荷-位移曲线拟合，又考虑应力匹配[17]。选择表征应力应变(εr,σr)与本构方程之间的匹配作为优化准则。参数的优化准则是采用了卸载开始点处的表征应力应变与本构关系曲线的最佳匹配，并没有将卸载段作为相应数据考虑在内。

err=∑min[σr(h)-σr(h,p)]

(15)

其中:

式中，σr(h)为压痕深度h处的表征应力;P(h)和a(h)分别表示压痕深度h处的载荷P和接触半径a;σ(h,p)和ε(h)分别表示用参数p(σy,n,K)构造的本构方程中应力和应变;P(h)和a(h)的值可以通过神经网络模拟得到。根据标准ISO/TR 29381—2008中的参数取值，ψ=3，α=0.14。

3 测试结果

3.1 压痕曲线测试结果

采用IIT-2000型压痕仪得到压入试验的载荷-位移曲线，压痕仪的最大载荷为2 000 N，位移精度为0.2 μm，压头为直径1 mm的碳化钨球，试验材料为304不锈钢和316L不锈钢。利用试验得到的多循环压痕曲线，神经网络法计算结果如图7所示。

(a)304不锈钢

3.2 球形压痕表征应力应变法测试值和单轴拉伸试验值的对比

按照GB/T 228.1—2010《金属材料 拉伸试验 第1部分:室温试验方法》，采用CMT5205型电子万能试验机进行单轴拉伸试验。试验材料为304不锈钢和316L不锈钢，拉伸试样的尺寸为∅10 mm×50 mm，试验温度为室温，拉伸速度为1 mm/min。

由表3可看出，神经网络法得到的σy,σu,n,E与单轴拉伸试验值偏差较小。神经网络法能够用于预测奥氏体不锈钢的力学性能且精度较高。

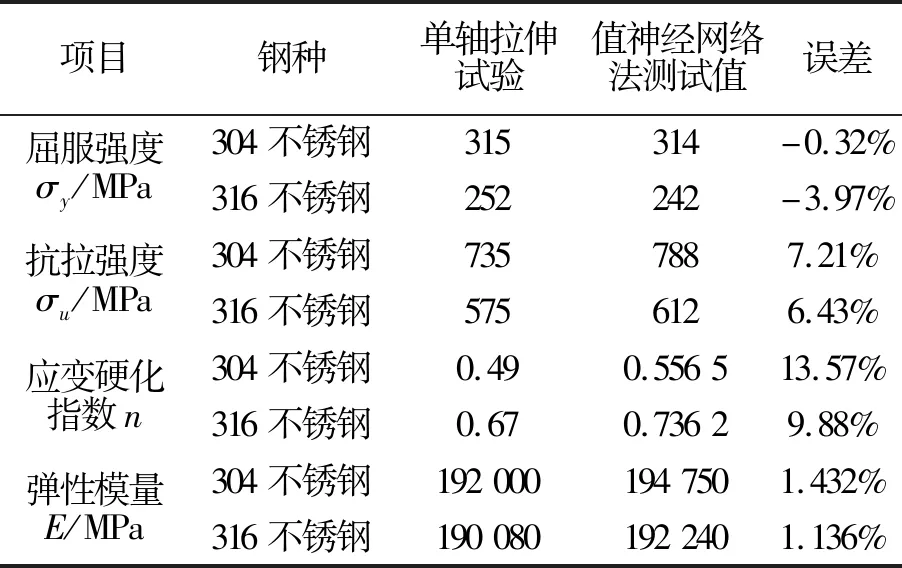
表3 神经网络法测试结果与单轴拉伸试验结果对比Tab.3 Comparison between the results of indentation test and uniaxial tensile test

4 结论

(1)Hollomon模型能够描述常见金属材料的加工硬化行为，但是无法描述奥氏体不锈钢等具有明显上翘行为的加工硬化曲线。采用Ludwik模型能够描述奥氏体不锈钢的应力-应变曲线。

(2)基于Ludwik模型，采用有限元软件进行仿真建立压痕曲线神经网络数据库，利用训练好的神经网络分析压痕曲线，计算奥氏体不锈钢的力学性能。

(3)神经网络法计算得到304和316不锈钢的屈服强度、抗拉强度、应变硬化指数和弹性模量等力学性能，与单轴拉伸试验结果相比，偏差较小，该方法能够用于预测奥氏体不锈钢的力学性能。