关于Kane难题的一种解决方案
张九铸
(金昌市龙门学校 甘肃 金昌 737100)
1 引言
如图1所示,质量为m1,半径为r1的均质刚性球壳绕其直径的转动惯量为J1,与刚性水平面进行斜碰.碰撞之初,球壳的质心速度为V01,与竖直的Oy轴负向的夹角为α,角速度ω01沿逆时针方向.球壳与水平面之间的碰撞恢复系数为e.再设上述各量能够保证:球壳碰撞点的水平初速度为v0x>0,球壳在整个碰撞过程中受到方向不变的动摩擦力且该力满足库仑摩擦定律,动摩擦因数为fd.由平面运动刚体动力学方程及恢复系数定义有
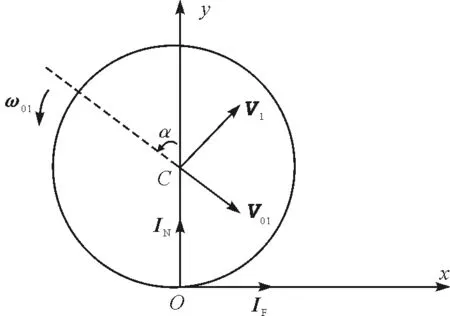
图1 刚性球壳与刚性平面之间的碰撞
-fdIN=m1V1x-m1V01sinα
(1)
IN=m1V1y-m1(-V01cosα)
(2)
-r1fdIN=J1ω1-J1ω01
(3)
(4)
其中IN是球壳在整个碰撞过程中受到的支持力的冲量,V1和ω1分别是球壳在碰撞过程末的质心速度和角速度,各矢量方向如图1所示.联立以上4式,可得到
V1x=V01[sinα-fd(1+e)cosα]
(5)
(6)
其中
系统在碰撞过程中的动能损失为
(7)
将式(5),式(6)代入式(7),得到
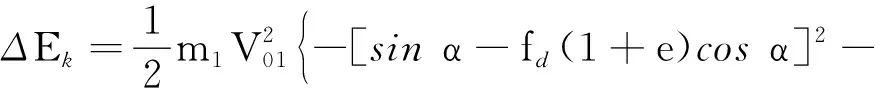
(8)
取具体数值α=30°,e=0.7,fd=0.4,a=0.30.将这些数值代入式(8),算得ΔEk<0,这显然不符合能量守恒定律.出现此类结果的问题称为Kane难题[1].
上述问题中的运动初始条件是合理的,解答过程中所用其他定理和公式也是合适的,故Kane难题产生的原因,只能是用库仑摩擦定律If=fdIN将法向冲量大小IN和动摩擦力冲量大小If联系起来这一点,进一步讲,仅由上述运动学条件(V01,α,ω01)、几何条件(r1)、动摩擦系数fd和恢复系数e这6个量无法确定球壳碰撞过程各阶段的受力或各力之间关系,当然也无法保证球壳在碰撞过程中始终受的是满足库仑摩擦定律Fτ=fdFN的动摩擦力.实际上,在碰撞过程各阶段,球壳与水平面之间的接触力比较复杂.比如两个弹性球体的碰撞,且接触面是一个圆面,如图2所示.
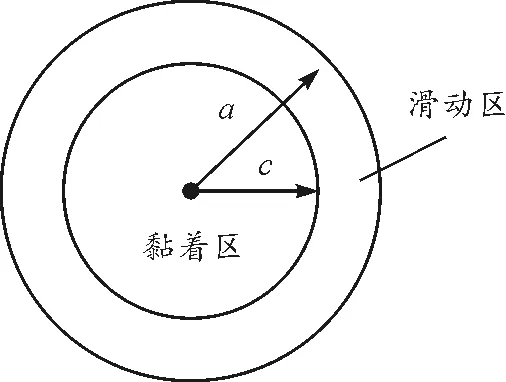
图2 两个弹性球之间的存在切向力时的接触面
则碰撞过程中某些阶段还可能出现这种情况:两球之间的总法向力大小根据赫兹分布[2]应为
(9)
而接触面之间的总切向力可用公式[2]
(10)
计算.以上二式中的a为接触面半径,c为黏着区(该区域内,两球之间因分子间范德瓦耳斯力而相互吸引)半径,c 鉴于此,笔者建议,仿照针对二碰撞点沿二刚体公法线的运动我们定义了可通过实验测定的恢复系数e,现在也可以定义一个绝对值小于等于1的并且也可以通过实验测定的“切向恢复系数k”,即二碰撞点的切向相对末速度与切向相对初速度之比.诚然,由式(10)和式(1)、(3)可知,式(7)中必然有 V1x≤V01x ω1≤ω01 即ΔEk一定大于等于零.而由以上二式得到 V1x+r1ω1≤V01x+r1ω01 即圆球碰撞点的初、末速度满足 为不失一般性,以下我们导出两个作平面运动的刚性球碰撞过程中的、含参量k的动能损失计算式,继而找出关于k值的满足能量守恒定律的范围. 设质点系中第i个质点的质量为mi,其在dt时间内的初、末速度分别为v0i和vi,合力(包括系统的内力和外力)的冲量为Ii合,则由质点动量定理,有 mi(vi-v0i)=Ii合 先用vi标乘上式,再用v0i标乘上式,然后将两个结果相加,得到 (11) 将质点系中所有质点的相似方程相加,得到系统的动能损失为 (12) 上式中Ii已不再含有mi所受系统的内力. 现在将式(12)运用于两个始终做平面运动的刚体的碰撞,且设只有一对碰撞点,如图3所示. 图3 二弹体的碰撞,单位矢量n和τ沿公法线和公切面 注意:同一刚体上所有内力做功之和为零,故式(12)右端这时只针对两个碰撞点.设碰撞初,二刚体角速度分别为ω01和ω02,二碰撞点速度分别为v01,v02;碰撞末,二刚体的角速度分别为ω1和ω2,二碰撞点速度分别为v1和v2;碰撞中二碰撞点受到的法向冲量分别为I1n和-I1n,切向冲量分别为I′1τ和-I′1τ,其中n和τ分别为法向单位矢量和切向单位矢量.则由式(12)得到 (13) 研究两个均质刚球的摩擦碰撞,如图3所示.定义法向恢复系数、切向恢复系数分别为 (14) 代入式(13),消去其中的末速度,得到 2ΔEk=-I1(1-e)(v01n-v02n)- (15) 先求I1.设在碰撞过程中,球1质心的初、末速度分别为V01和V1,球2质心的初、末速度分别为V02和V2,系统的折合质量为μ,则由两体运动动量定理,在n方向上有 I1=μ(v1n-v2n)-μ(v01n-v02n) 再用式(14)第一式将其改写为 I1=-μ(1+e)(v01n-v02n) (16) 再求I′1.由质心系中的角动量定理,对二刚球分别有 其中J1,J2分别是两个圆球对各自直径的转动惯量.以上二式分别乘以r1,r2,变为 (17) 由质心运动定理,二刚球在τ方向上分别有 (18) 将式(17)第一式与式(18)第一式相加,将式(14)第二式与式(18)第二式相加,且考虑 V1τ+ω1r1=v1τ V01τ+ω01r1=v01τ V2τ+ω2r2=v2τ 和 V02τ+ω02r2=v02τ 分别得到 两式相减,并且利用式(14)第二式,且令 (19) 得到 I′1=c(k-1)(v01τ-v02τ) (20) 将式(16)、(20)代入式(15),得到 (21) 由式(21)可知:因为0≤e≤1,所以,要恒有ΔEk≥0,则k值必须满足 -1≤k≤1 (22) 式(22)是式(21)成立的必要条件,即式(22)是能量守恒对k值的限制结果.我们以二刚体沿n方向做对心的完全弹性(e=1)碰撞的情形为例,来考查式(22)的物理意义.当k=1时,由式(14)第二式,这表示碰撞过程中二碰撞点在τ方向上的相对速度不变,即二圆球在碰撞中不受切向力,当然有ΔEk=0.当k=0时,二碰撞点在τ方向上的末相对速度为零,这类似于n方向上的完全非弹性碰撞,这时ΔEk最大.当k=-1时,表示二碰撞点在τ方向上的末相对速度与初相对速度等大而反向,这说明二圆球之间的切向力保证了二碰撞点在τ方向上无相对运动,且该方向上的碰撞过程类似于n方向上的完全弹性碰撞,故 ΔEk=02 动能定理的一种形式
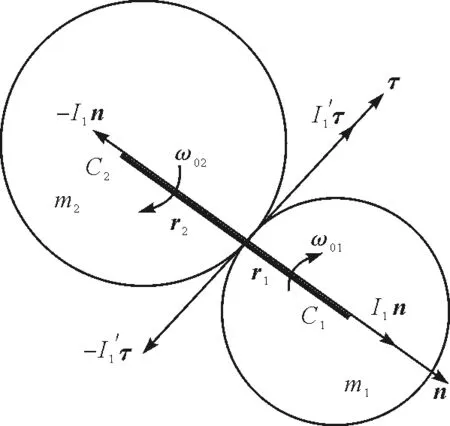
3 两个均质刚球在碰撞过程中的动能损失
I′1(1+k)(v01τ-v02τ)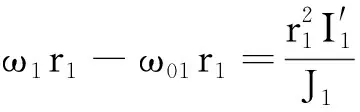

4 k值的范围及物理意义

