中学阶段对“落体偏东”现象的公式推导

张 明

(江苏省盱眙中学 江苏 淮安 211700)

1 引言

众所周知，初速度为零，只受重力的运动为自由落体运动，自由落体运动是由静止开始的匀加速直线运动，方向竖直向下[1].曾有学生向笔者提出，看到有资料书上介绍过自由落体运动并不是竖直向下的，落地点是偏向东的，这是怎么回事呢？ 为什么平时没有观察到落体偏东的现象呢？

2 难以观察的原因

如图1所示，在北半球纬度为λ的一质点从近地面高为h的地方自由下落，文献[2]中运用高等数学建立微分方程组，两次积分后得到轨道方程为

图1 北半球纬度为λ的经纬线

到达地面时z=0，偏东的距离[2]

(1)

若λ=40°，h=200 m,可算出y≈4.75×10-2m，偏东距离不足5 cm，故难以察觉.

显然，如果照搬大学教材，中学阶段的学生既没有理论力学知识的相关物理基础，也不具备相应的数学知识和运算能力，学生肯定是无法接受的.但是学生已经提出了问题，如何能让学生理解，有所收获呢？

3 近似为平抛运动

有学生提出平抛运动模型：在距地面一定高度的物体，由于随地球自转而具有的线速度，大于地面上物体的线速度.所以该物体下落时必然相对地面有一个偏东的速度，落点自然就会偏东如图2所示.

图2 平抛运动模型

物体相对地面向东的水平速度为

v=ω(R+h)cosλ-ωRcosλ=ωhcosλ

(2)

y≈7.5×10-2m

即约为7.5 cm，比式(1)算出结果略大，但两者数量级相同，因此，看作平抛运动也具有一定的意义，因为中学生对平抛运动是熟悉的，在离地不是太高，计算精度要求不高时，可以作为数量级的估算.

4 用微元法推导

地球绕地轴转动，是一个转动参考系.在地球非惯性系中，相对地球运动的物体要受到惯性力——科里奥利力F=-2mω×v的作用，对于落体运动v=gt，物体下落时受到一个水平向东并逐渐增大的力，在北半球纬度为λ产生的加速度大小a=2ωgtcosλ[2,3].式(2)之所以出现偏差，就是因为水平方向不是匀速的，而是从静止开始有一个逐渐增大的加速度.若将加速度作为已知条件，则落体偏东现象可以归结为一个中学生可以理解并能解决的问题，即求解一个变加速直线运动.

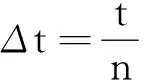
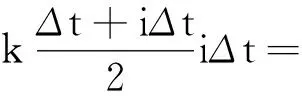
上式中(1+i)i略去i的一次项小量，则

(1+i)i≈i2

可得

利用数学公式

则

略去小量可得

(3)

与式(1)相同.

5 上抛偏西

如果将一个物体竖直向上抛出，同样由于科里奥利力F=-2mω×v的原因，上升过程有向西的加速度，向西的水平速度逐渐增加，而下降过程有向东的加速度，向西减速运动，落地点实际偏西.基于同样的方法可以推导出定量的结果，这里就不赘述了.

中学阶段，作为背景知识，多了解不仅可以拓宽视野，对高考也不无裨益，试举例：

【例题】(2018年高考北京理综第20题)根据高中所学知识可知，做自由落体运动的小球，将落在正下方位置.但实际上，赤道上方200 m处无初速下落的小球将落在正下方位置偏东约6 cm处，这一现象可解释为，除重力外，由于地球自转，下落过程小球还受到一个水平向东的“力”，该“力”与竖直方向的速度大小成正比，现将小球从赤道地面竖直上抛，考虑对称性，上升过程该“力”水平向西，则小球( )

A．到最高点时，水平方向的加速度和速度均为零

B．到最高点时，水平方向的加速度和速度均不为零

C．落地点在抛出点东侧

D．落地点在抛出点西侧

基于题目的已知条件，可以分析出D为正确选项.

目前高考题越来越灵活、新颖，背景知识也越来越广阔.对于很多平时善于思考、勇于拓展和学习相关课外知识、努力提升综合能力的学生，在高考中面对以课本上没有出现过的知识为背景的试题时，无论见过与否，有了平时的历练和素养，会更快、更容易地做出结果.

6 结束语

在北半球，河流右岸的冲刷甚于左岸，右岸相对陡峭；火车铁轨的右轨所受到的压力大于左轨，因而磨损相对严重[2]；夏秋之际，在我国东南沿海经常出现的台风，是逆时针流动的气旋.南半球的情况刚好相反.这些现象与落体偏东现象，背后都是科里奥利力在起作用.

在中学阶段，了解科里奥利力的意义不仅仅是为了掌握多少知识，更重要的是拓展学生科学视野,激发学习兴趣，培养勇于探索的科学精神.