导体棒旋转切割磁感线模型的解决新法

程宏远

(新乡市第一中学 河南 新乡 453000)

导体棒旋转切割磁感线模型一般解决方法是法拉第电磁感应法和等效速度法[1]，这两种方法在学生理解和解决问题层面具有一定的局限性.法拉第电磁感应法是定律的应用，对学生掌握定律非常有益，但是磁通量的变化量在复杂情况中很难计算.等效速度法是利用导体棒上每一点的线速度与半径成正比的关系，得到导体棒中间位置线速度可以作为整个导体棒等效速度，从而利用动生电动势公式求解电动势.徐洪图等人已证明平均速度法对于直导体棒绕任意点旋转切割均成立[2]，然而得到等效速度过程对于学生思维理解的台阶过高.这两种传统方法可以解决旋转点在导体棒上和导体棒延线上的问题，但对于旋转点为平面内任意一点的情况以及导体棒弯曲的情况难以解决.旋转切割的复杂情况需要微分的方法，但是高中学生缺乏相关理论知识，需要用简化可行的方法帮助学生理解和解决问题.

本文在微分思想的指导下，利用图像和微元相结合的方法，创新解决导体棒旋转切割磁感线的系列问题，得出此类问题的一般结论.旋转切割问题中使用图像与微元法，不仅解决旋转切割的各类问题，也扩展高中物理阶段微元法的应用范围，培养学生科学思维.

1 导体棒直线任一点作为旋转点

1.1 导体棒端点作为旋转点

如图1所示，导体棒Oa绕端点O旋转.

图1 旋转点为导体棒端点

导体棒上每一点线速度不同，要利用动生电动势公式E=BLv求解导体棒产生的电动势，需要解决速度与长度乘积问题.我们将导体棒切割成n段，总电动势等于每一段导体棒产生电动势之和.每段导体棒长度ΔL非常短，可视为一个点，所以每段导体棒切割速度近似可用前端线速度代替.如图2所示，每段导体棒速度与长度乘积在图像中表现为小矩形的面积，整个导体棒速度与长度乘积就是各个小矩形面积之和，即图像与横轴所围三角形面积ΔS.

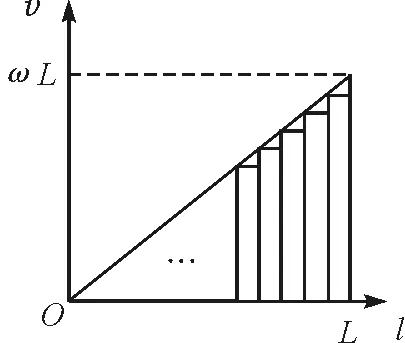
图2 导体棒各点速度v与到O点距离l关系图像

E=BΔL1v1+BΔL2v2+…+BΔLnvn=

1.2 导体棒之间一点作为旋转点

如图3所示，导体棒ab绕棒上点O旋转.

图3 旋转点为导体棒上一点(非端点)

导体棒ab看作两部分Oa和Ob，每部分产生的电动势可由1.1中结论得到.由右手定则得到两部分电动势方向不同，E为

1.3 导体棒延线上一点作为旋转点

如图4所示，导体棒ab绕延线一点O旋转.

图4 旋转点为导体棒延线一点

我们依然把导体棒ab分割成n段，每段vΔL是小矩形的面积，导体棒整体vL就是图像与横轴所围梯形面积，如图5所示.

图5 导体棒各点速度v与到O点距离l关系图像

1.2和1.3结果相同，因为1.2中导体棒Oa和Ob产生的电动势相抵消后与1.3中所描述情况一致.

2 导体棒旋转点为平面内任意一点

如图6所示，导体棒ab绕平面一点O转动，Oa和Ob分别为L1和L2(L2>L1)

图6 旋转点为导体棒平面一点

方法一：微元图像结合法

导体棒ab分割成n段，每段导体速度与长度成夹角θ，且各段夹角不同.我们把每段长度ΔL分解到垂直速度的方向上，得到ΔLcosθ，则这段导体产生电动势表示为ΔE=BΔLvcosθ.各点速度v与到旋转点O的距离l仍满足图5，各段速度与长度乘积是图5中小矩形面积，则整段导体棒速度与有效长度的乘积是图5中图像与横轴所围梯形面积.

方法二：有效长度法

导体棒各段长度分解到垂直速度方向的长度叠加后，长度等效为导体棒ab沿半径方向分量a′b′长度，即L2-L1为导体棒的有效长度.导体棒ab产生的电动势等效为导体棒a′b′产生的电动势.我们假想有Oa和Ob两根导体棒与导体棒ab结合，则导体棒ab产生的感应电动势等于Oa和Ob两根导体棒产生的感应电动势之差.

导体棒旋转点为平面内任意一点的旋转切割题目非常灵活，见以下两道例题.

【例1】如图7所示，直角形导体棒abO绕O点旋转，ab和Ob长度分别为L1和L2,求EOa.

图7 直角导体棒绕端点旋转

解析：导体棒abO产生电动势可分解为Ob和ba两根导体棒产生电动势之和.

EOa=EOb+Eba=

【例2】如图8所示，导体棒abc中点为b，绕O点旋转，导体棒abc垂直直线Ob,求Eac.

图8 “一字型”导体棒绕中垂线一点旋转

解析：导体棒abc产生电动势可视为ab和bc两根导体棒产生电动势之和.两根导体棒有效长度相同，产生电动势等大反向，即Eac=0.

3 曲线导体棒绕导体棒平面一点旋转

如图9所示，曲线导体棒ab绕O点旋转.

图9 曲线导体棒绕平面一点旋转

导体棒ab为曲线，我们利用微元法的思想将其分割为n段，每段导体速度与长度成夹角θ，每段长度ΔL分解到垂直速度的方向上得到曲线的有效长度也为径向长度，速度与有效长度关系图像与图5相同.故曲线导体棒ab产生感应电动势的表达式为

4 导体棒旋转切割磁感线模型一般结论

本文论证均为导体棒在垂直于匀强磁场平面旋转切割磁感线的前提下提出，根据以上讨论可得到以下3条结论.

(1)微元图像法解决公式中导体棒速度与长度乘积问题.我们作出导体棒速度与旋转点距离关系图像，经过微元法处理，得到图像与坐标轴所围面积的含义即为导体棒速度与长度的乘积.

(2)导体棒旋转切割磁感线模型存在有效长度.无论导体棒是曲线还是直线，“有效长度”都等于将导体棒投影到半径方向的长度.

(3)导体棒切割磁感线产生的感应电动势可以通过两种思路求解.一是利用电动势E=BLv求解，其中Lv为图像与横轴所围面积；二是利用电动势等于“有效长度”导体棒产生的感应电动势求解.