对称单极柔性直流输电系统不对称交流故障解析模型

曹润彬，聂少雄，芮智，黄伟煌，郑伟，国建宝，杨光源，舒德兀

(1.直流输电技术国家重点实验室(南方电网科学研究院)，广州510663；2. 电力传输与功率变换控制教育部重点实验室(上海交通大学)，上海200240；3. 南方电网超高压输电公司检修试验中心，广州510663)

0 引言

由于开关频率低、损耗小，输出谐波小、模块化设计方便等优势，模块化多电平换流器型高压直流(modular multi-level converter high voltage direct current，MMC-HVDC)系统已成为柔性直流输电领域的重要发展方向[1-3]。近年来在柔性直流输电系统中出现背靠背直流输电工程，采用简单的对称单极系统结构。直流侧无接地极干扰，已在工程中加以使用[4-5]，对称单极结构柔性直流输电系统也是本文的主要研究对象，其结构如图1所示。

图1 MMC-HVDC系统对称单极结构示意图Fig.1 Symmetric single-pole structure diagram of MMC-HVDC system

柔性直流输电系统的相关研究主要集中在拓扑结构的优化以及控制策略的制定[6-8]，而近年来随着柔性直流工程电压等级的升高和容量的增大，故障电流对于电力设备正常工作及系统正常运行造成严重威胁[9]，因此对故障机理的研究成为了焦点，其中故障电流的计算与描述是控制保护策略制定、电网参数设计、器件选型的重要基础[10-11]。

柔性直流输电系统领域计算故障电流一般使用PSCAD等电磁暂态仿真软件搭建仿真模型计算求解。实际工程应用中搭建仿真模型较为复杂，且耗时长，具有一定局限性[12-13]。例如在鲁西直流工程或者乌东德直流工程的保护整定计算中，每5 s电磁暂态仿真通常需要耗费20 min左右。而每次保护整定需要对上百个工况进行电磁暂态仿真。因此避免采用耗时的电磁暂态仿真，采用故障解析计算分析对柔性直流输电系统进行保护整定是本文关注的重点。

当MMC-HVDC交流系统出现不对称故障时，功率的波动引起子模块能量分布改变，影响换流器输出特性。国内外对柔性直流系统交流不对称故障短路电流的研究中，文献[14]进行了柔性直流系统联结变阀侧单相接地故障的机理分析。并提出了保护策略的改进建议，但没有得到短路电流的具体表达式；文献[15]探究了MMC在不平衡运行条件下的数学模型，并设计了新型不平衡条件下的控制器，但没有区分控制保护系统响应前后的故障过程；文献[16]研究了单相接地故障对换流器内部环流的影响，并提出了环流抑制方法，但没有得到交流线路短路电流的定量表达式。交流不对称故障解析模型的难点在于如下几个方面：1)柔性直流交流不对称故障发生过程不仅受到主回路电气参数的影响，同时受到离散动作保护以及阀控和极控的影响；2)柔性直流的阀控和极控相互影响并且相互制约，动态特性复杂。

为了解决上述问题，本文针对真实的对称单极结构柔性直流输电系统，建立并分析交流不对称故障后的数学模型，对故障后控制器响应前后短路电流动态特性建立解析公式，并通过真实柔性直流工程的仿真对比进行验证。该方法省去建立仿真模型步骤，定量描述故障后短路电流的变化情况，为控制保护策略的设计和优化提供参考，对实际工程具有重要应用价值。

1 柔性直流换流阀交流不对称故障解析模型

1.1 交流不对称故障初始动态过程

本文将对故障发生后控制器响应前后的过程进行分析。故障发生后最初的数百微秒内，换流器控制保护系统的采样、通信、计算等过程需要一定的响应时间，本节对此过程也进行分析。首先建立以下假设：该阶段时间极短，认为子模块电容电压基本保持不变。同时由于非故障侧的支撑作用，认为直流侧电压保持不变。由此建立交流对称故障时故障相和非故障相的等效模型如图2所示。

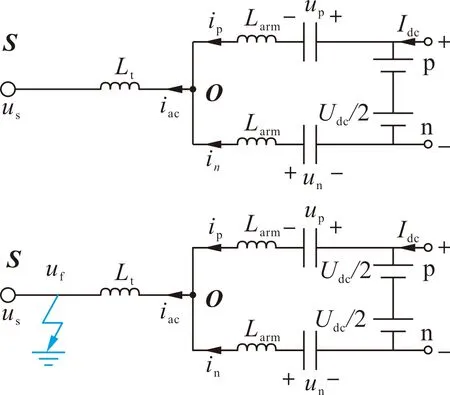
图2 MMC-HVDC系统中故障相与非故障相等效模型Fig.2 Equivalent model of faulty phase and non-fault phase in MMC-HVDC system

以A相接地故障为例，换流器运行状态及桥臂电压不变，故障点处电压迅速下降，两者的压差降落在桥臂电感和变压器等效电感上，桥臂电流急剧上升。根据等效模型及基尔霍夫电压电流定律得到过电流过程中的故障相(A相)和非故障相(B、C相)的电压电流方程如式(1)—(3)所示。

(1)

(2)

(3)

式中：Larm为桥臂电感；Lt为变压器等效电感；us为交流母线电压；up、un为上下桥臂电压；ip、in为上下桥臂电流；uf为故障点处电压；Udc、iac为直流侧电压与交流侧电流；下标abc分别表示电气量在abc三相的分量。

根据基尔霍夫电流定律，桥臂电流与交流线路电流之间存在的关系如式(4)所示。

iac_i=ipi+ini,i=a,b,c

(4)

由此计算A相接地故障下桥臂电流与交流线路电流的上升速率，如式(5)—(6)所示。

(5)

(6)

可以看出，短路电流在该过程中均以直线形态上升。对于故障相，短路电流最大上升率出现在MMC满调制、交流侧相电压跌落为0，故障发生在稳态电流峰值时；对于非故障相，当MMC满调制，交流电源电压达到峰值时，非故障相出现最大电流上升率。

本节得到了在MMC-HVDC发生交流侧不对称故障时，桥臂电流及交流线路电流的上升速率。由于不对称故障较为轻微，控制器响应前后短路电流的变化并不明显，但整体变化趋势仍满足上述数学模型。

1.2 交流不对称故障初始动态过程

在MMC-HVDC系统中，交流电网不对称会导致电气量出现正序和负序分量，换流器交流侧电流不平衡，交流侧三相瞬时功率之和变为时变波动量，产生功率振荡。同时直流侧出现较大的二倍频电流和电压波动等问题，危及系统的安全稳定运行，尤其是交流电网发生不对称接地故障时，问题更加严重。

交流侧发生不对称故障时，MMC换流站的输出的有功功率p(t)和无功功率q(t)可以表示为：

(7)

式中：p0、q0分别为有功功率和无功功率的平均值；pc2、ps2分别为有功功率的二倍频余弦与正弦谐波分量的峰值；qc2、qs2分别为无功功率的二倍频余弦与正弦谐波分量的峰值；ω为角频率；3u0i0项表示零序分量，本文中忽略。则式(7)各项参数可以由式(8)得到。

(8)

式中：u、i分别为交流电压及电流；下标d、q分别表示d轴和q轴分量：上标P、N分别表示正序和负序分量。

不对称故障下，应当在控制策略中体现对正负序电流的控制，即对正序和负序电流分别进行控制，需要进行正负序分解。

在正负序分解的dq域解耦下，应当满足：

(9)

式中上标“*”表示该电气量的参考值。这里需要特殊说明，实际柔性直流极控中包含正序控制和负序控制。但是本文所涉及的某实际直流工程中的负序控制对应的参考值设置为0。

三相电压满足式(10)：

(10)

式中：UP、ω和θp分别为正序电网电压的幅值、频率和相位；UN和θn分别为负序电网电压的幅值和相位。式(10)经过克拉克变换后可得αβ坐标系下电网电压uα和uβ为：

(11)

最终可以得到：

(12)

式中上标P、N分别为uα和uβ的正序和负序分量。

(13)

根据上述结果，可以得到正负序分解的框图如图3所示。

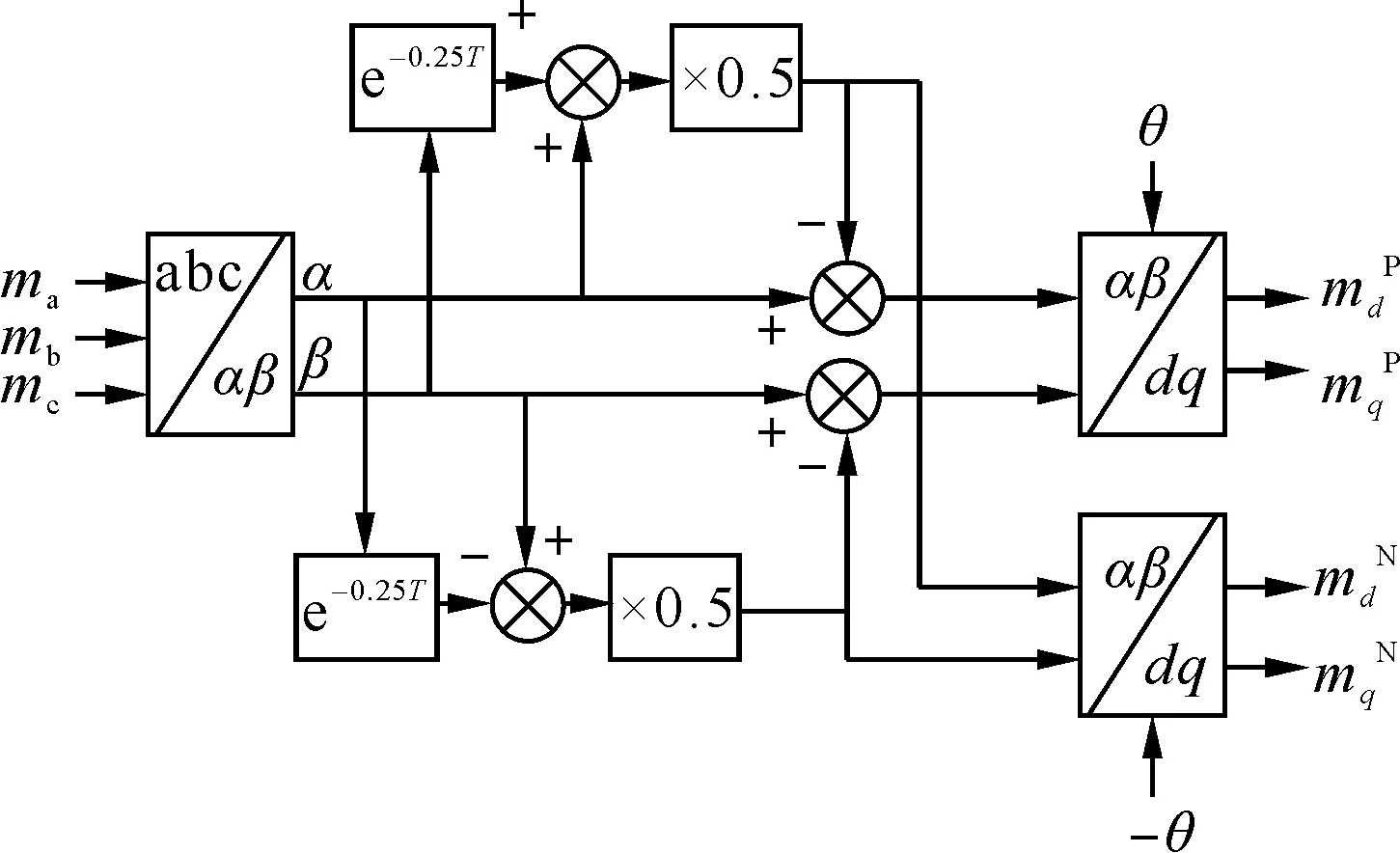
图3 三相交流电气量转换为正负序示意图Fig.3 Diagram of converting three-phase AC electrical quantity into positive and negative sequence

由此完成了对交流侧电压电流的正负序分解。在适当的控制策略下，直流电压二次谐波分量被消除，因此有功功率的二次谐波分量为0，即pc2=ps2=0。正常运行状态下，换流站无需传递无功功率，因此q0=0。由此得到有功和无功电流的正序及负序分量的参考值如式(14)—(15)所示。

(14)

式中p0*为电压外环的有功功率参考值。

p0*=udc*(kp_outd+ki_outd/s)(udc(s)-udc*)

(15)

式中：s为拉普拉斯变换中的复频率变量；kp_outd和ki_outd分别为外环PI控制的比例参数和积分参数的d轴分量。

根据基尔霍夫定律以及派克变换的基本原理，MMC输出电压的d轴分量可以表达为：

(16)

式中Rs、Ls分别为交流侧等效电阻与等效电感。

由前文分析，ud也可以表达为：

·学位论文[序号]作者.题名[D].学位授予单位所在城市名：学位授予单位，授予年份.数字对象唯一标识符

(17)

式中kp_ind和ki_ind分别为内环PI控制的比例参数和积分参数的d轴分量。

(18)

其中

(19)

(20)

其中

(21)

式中：K1、K2、D1为关于idp的二阶微分方程系数；ξ1、ω1分别为二阶系统的阻尼比和自然角频率；δ1为微分方程解的初始相位。

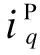
(22)

其中

(23)

式中kp_inq和ki_inq分别为内环PI控制的比例参数和积分参数的q轴分量。

2 柔性直流换流阀交流不对称故障仿真分析

2.1 仿真模型介绍

本文使用仿真模型为国内某实际直流工程模型，采用MMC-HVDC对称单极结构。以单相接地故障为例，故障设置在换流变压器与交流电源之间，系统功率为额定功率。该系统对应的典型参数如下：交流电压为525 kV；直流电压为±350 kV；子模块数为335个；子模块电容为8 000 μF；桥臂电感为105 mH。

2.2 极间故障第二阶段

为了验证上述数学模型的正确性，在某实际直流工程电磁暂态模型中的交流侧设置了单相接地故障，根据得到的故障解析模型，将三相交流电流分解为d轴正序分量和q轴正序分量，分别得到了其表达式，随后得到三相电流的解析模型。将模型与实际工程模型的仿真进行对比。

实际研究中发现，换流变压器与交流电源之间的单相接地故障不会触发保护动作，短暂故障下系统有足够的故障穿越能力。此时，以联接变压器阀侧三相电流的正序分量作为保护整定强相关电气量，对比数学模型中与相关电气量与实际仿真得到的波形，并进行对比分析。

交流侧单相接地故障d轴及q轴短路电流波形对比如图4所示。由于故障较为轻微，初始动态过程表现不显著，控制系统迅速响应。故障后，无功电流参考值上升，导致d轴电流实际值上升。6 ms时无功电流参考值变为-0.3 kA，在控制系统作用下，d轴正序电流下降，随后在0.2 s稳定，d轴正序电流达到稳态值-0.85 kA。同时，q轴正序电流迅速上升，在0.1 s稳定至参考值-0.3 kA。

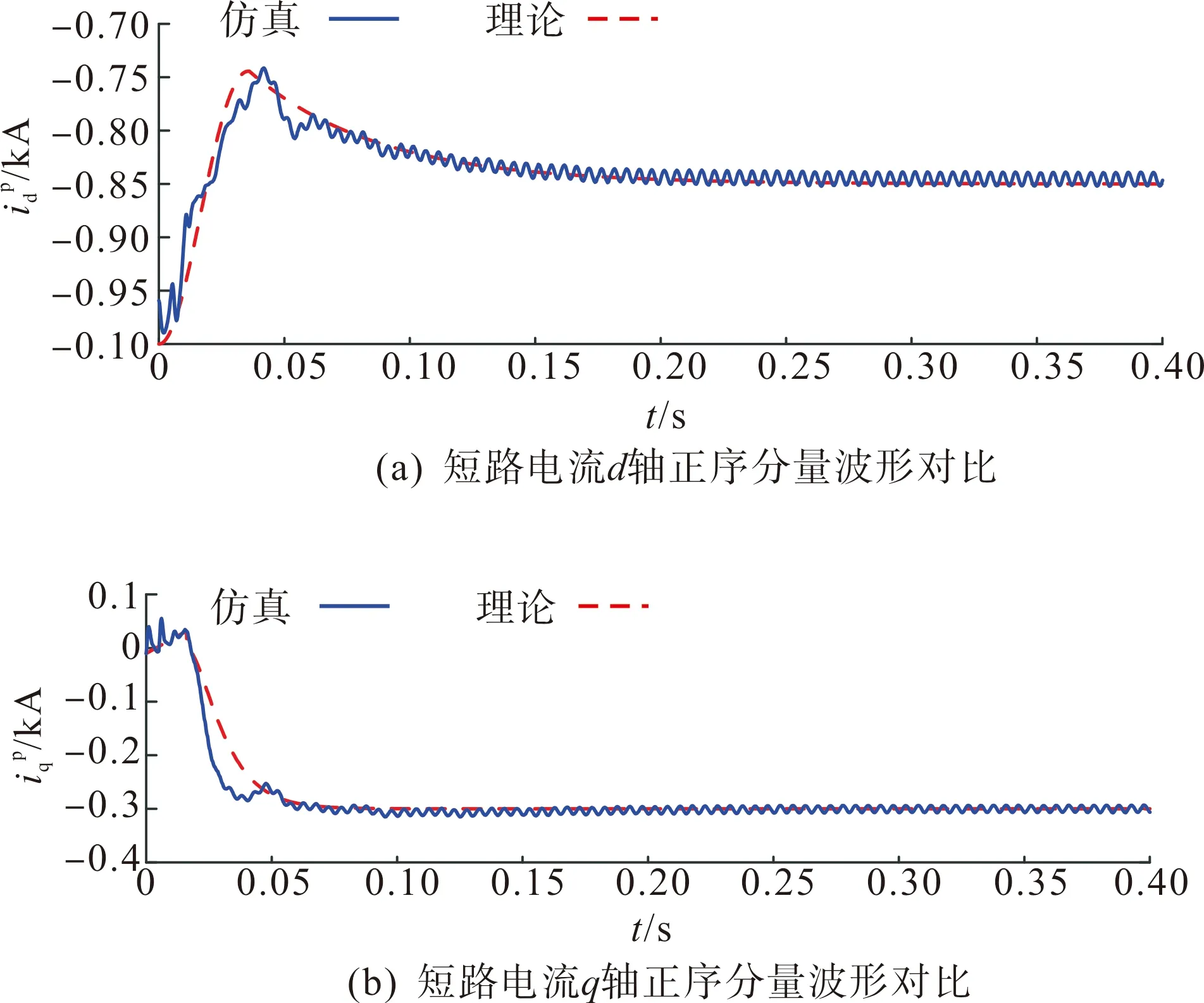
图4 交流侧单相接地故障d轴及q轴短路电流波形对比Fig.4 Comparison of d-axis and q-axis short-circuit current waveforms of AC single phase ground faults

将短路电流d轴与q轴分量通过反Park变换得到三相短路电流的波形，比较计算波形与实际工程仿真，如图5所示。短路电流自然上升后略微衰减，随后恢复至稳态。故障解析模型与实际工程仿真得到的波形非常吻合。

2.3 故障解析模型参数灵敏度分析

由模型理论分析可知，不对称短路故障下，线路电感L对正序d轴电流和q轴电流都有相应影响。因此针对线路电感L进行参数扫描，即改变线路电感L，观察短路电流id正序分量的波形变化。

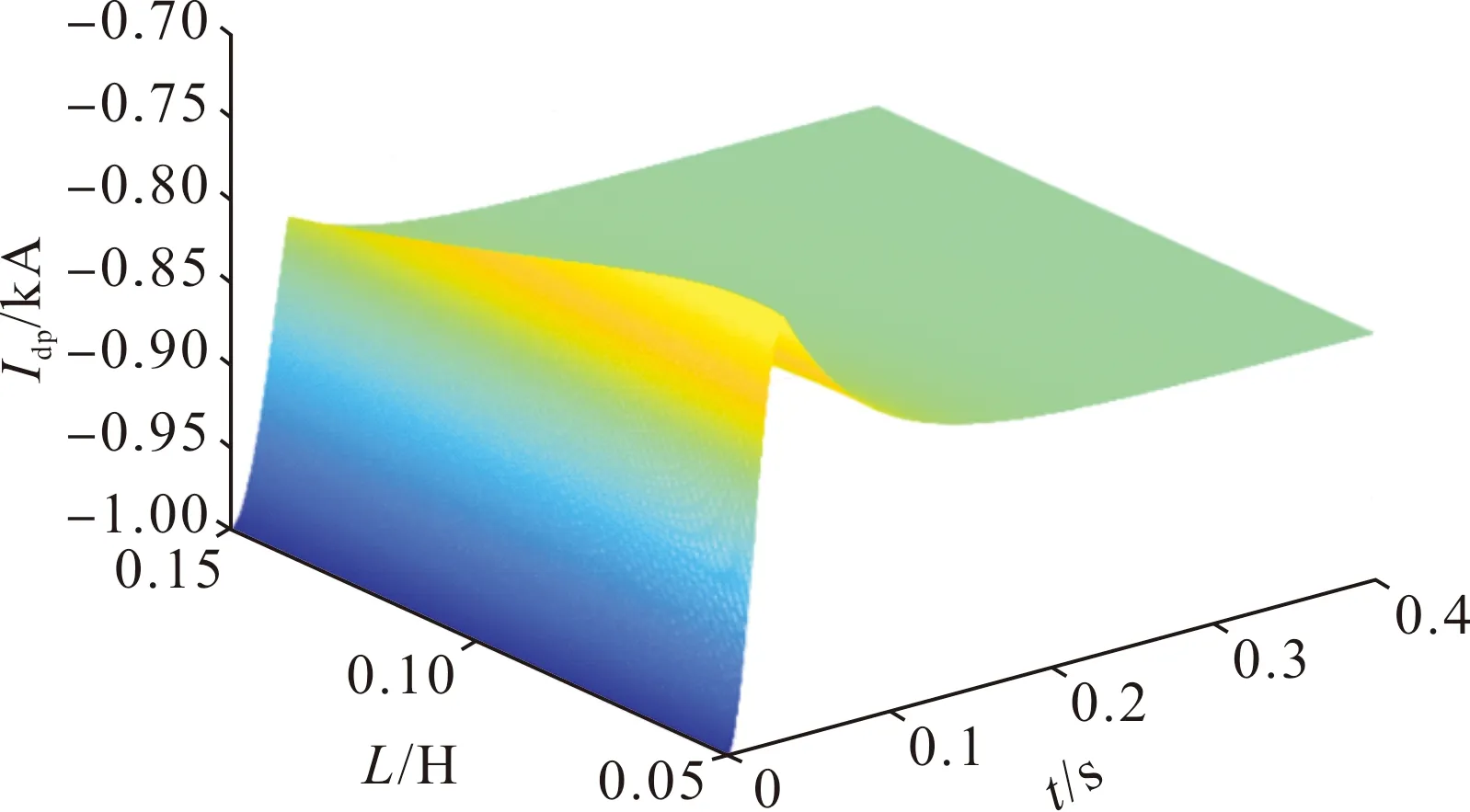
图6 单相接地故障不同电感值下d轴正序短路电流灵敏度分析Fig.6 Sensitivity analysis of d-axis positive sequence short circuit current under different inductance values of single phase to ground fault

通过对柔性直流换流阀的建模与分析，控制参数仍会对短路后电气量产生影响，为了分析控制参数对交流故障电气量的影响，以便进行后续保护整定工作，可以对控制参数进行灵敏度分析，如图8—9所示。控制参数的变化范围根据工程经验选取。

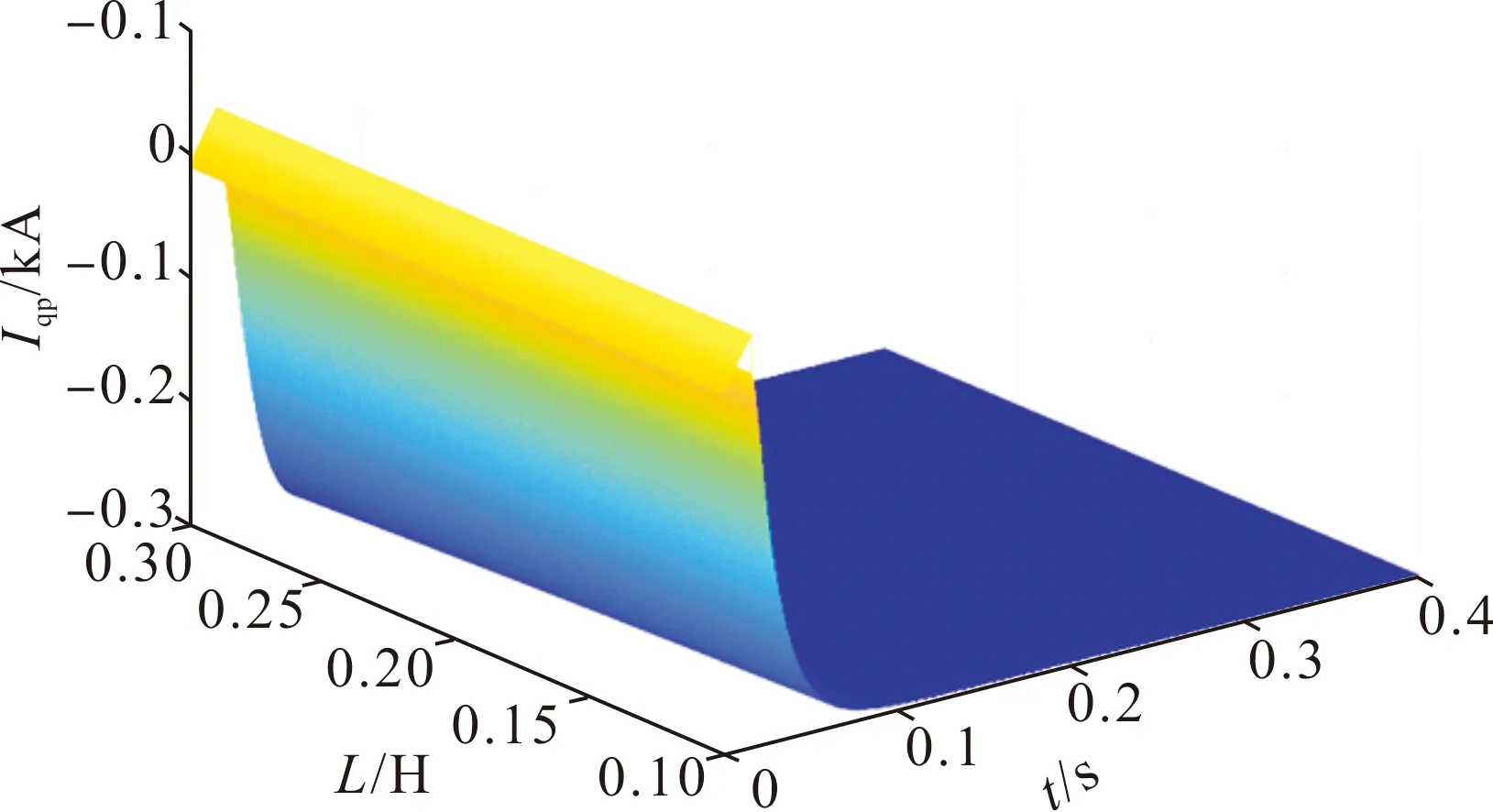
图7 单相接地故障不同电感值下q轴正序短路电流灵敏度分析Fig.7 Sensitivity analysis of q-axis positive sequence short circuit current under different inductance values of single phase to ground fault

图8 交流单相接地故障不同kp值下d轴正序短路电流灵敏度分析Fig.8 Sensitivity analysis of d-axis positive sequence short circuit current under different kp values of single phase to ground fault

由d轴正序电流的控制参数kp_ind的灵敏度分析可知，kp越小，d轴短路电流振荡情况越明显，变化范围越大，并且稳定时间越慢；由q轴正序电流的控制参数kp_inq的灵敏度分析可知，kp_inq越小，q轴正序短路电流振荡情况越明显，控制器响应后短路电流q轴正序分量峰值越大，稳定时间时间越慢。

图9 单相接地故障不同kp值下d轴正序短路电流灵敏度分析Fig.9 Sensitivity analysis of d-axis positive sequence short circuit current under different kp values of single phase to ground fault

通过上述仿真分析，可知采用本文所提出的交流故障解析模型相比于时域电磁暂态仿真有如下优势。

1)不需要经过电磁暂态仿真继而可以得到交流故障解析表达式，不仅为直流保护整定中的过电流保护和差动保护提供依据，同时避免了电磁暂态仿真过于耗时的弊端。

2)通过交流故障解析表达式可以清晰地了解交流故障典型电气量保护整定值的影响因素，为直流保护优化和参数整定值提供理论指导。

3)通过交流故障解析表达式可以了解故障不同阶段波形产生的机理，继而分析清楚影响故障电流主导因素是电气参数、控制器参数还是保护参数等。

3 结论

本文针对对称单极结构柔性直流输电系统交流不对称故障，建立故障下控制系统响应前后短路电流的解析模型，并与真实直流工程仿真模型比对，验证了解析模型的正确性，得到以下结论。

1)不对称故障控制系统响应前，桥臂电流与交流线路电流呈直线上升，根据线路参数可以得到其上升速率。

2)不对称故障控制系统响应后，交流线路短路电流进入衰减过程，参考值变化并最终稳定至故障后参考值。解析模型与实际仿真波形吻合。

3)本文推导的交流不对称故障解析模型可以指导保护整定策略，在应用中省去了搭建仿真的步骤，更为简洁快速。根据工程参数计算交流不对称故障下短路电流的动态过程，得到短路电流的变化情况，使得工程研究人员可以更好地设计控制与保护策略。