特高压混合直流输电系统中串联换流器的电压分配策略
黄剑湘,韩建伟,杨涛,李少森,陈诺,孙豪
(中国南方电网有限责任公司超高压输电公司昆明局,昆明650217)
0 引言
随着电力电子器件和控制技术的发展,常规直流(line commutated converter-high voltage direct current,LCC-HVDC)在异步联网、大功率远距离输电、海底电缆输电等诸多场景中有着十分广泛的应用[1-3]。20世纪80年代末,我国在浙江舟山投运了首个直流输电工程。虽然我国直流输电起步较晚,但经过30多年的理论技术和实践经验积淀,已成为全球直流大国。伴随着直流系统核心设备老化、辅助设备损坏、控制保护系统落后和接地装置腐蚀严重等问题的不断凸显,最早一批投运的直流工程正面临设备改造、技术革新、系统优化等问题,以保证这些直流系统的长期稳定运行[4]。
近年来,采用电压源型换流器的柔性直流输电(voltage source converter-high voltage direct current,VSC-HVDC)因具备有功无功功率解耦控制、无需消耗无功功率、无换相失败问题等优势而备受关注[5]。然而,柔性直流存在换流器造价昂贵、电压等级低、输电容量小等缺点。因此,有学者提出了混合直流输电系统[6],混合直流输电系统结合常规换流器和柔性换流器的技术特点,通过取长补短形成了一种新型直流输电拓扑结构。基于这种拓扑改造思路,将现有常规直流输电工程的受端换流站升级改造为柔性直流换流站,能够在节省造价、减少损耗的同时,解决换相失败困扰和提升系统灵活性[7]。
目前,针对常规直流改造为混合直流输电系统的研究,文献[8]从混合直流输电系统的主回路拓扑、换流器拓扑、控制保护技术等方面进行了归纳总结,并指出混合直流的技术难点和未来前景。文献[9-11]针对直流系统的直流故障自清除问题,提出了受端柔性化改造的混合直流技术方案。文献[12-14]分别基于直流电网、多端直流、新能源的应用场景,提出了多换流器混合连接的结构方式及控制策略。文献[15]研究了串联型混合直流输电系统,根据常规换流器和柔性换流器主设备参数间的耦合关系,提出了柔性直流主设备参数的非线性规划计算方法,并建立了受端LCC和VSC换流站各自承担400 kV电压(即LCC和VSC换流站的额定电压配比为1:1)的电磁暂态模型。文献[16]设计了受端由1个LCC与3个并联MMC(模块化多电平换流器)串联形成的特高压混合级联系统,通过分析多个并联MMC站间不平衡电流的产生机理,提出了一种基于电流不平衡量的功率补偿均衡控制策略。文献[17]提出将多个并联VSC通过直流联络线串联接入双极LCC系统的混合直流输电系统,系统中LCC与VSC的电压比例为500 kV:300 kV, 但对于该电压比例的选择依据并未充分说明。基于上述分析,本文借鉴白鹤滩—江苏特高压直流工程的混合级联多端思想[18],构建受端串联型特高压混合直流输电系统,突破传统高、低端换流器1:1的电压比例限制,通过优化VSC换流站容量,确保经济性的同时维持系统安全稳定运行。因此,定量分析系统受端LCC和VSC换流器的电压比例是本文的研究重点。
本文针对特高压混合直流输电系统中两种换流器串联时的电压比例问题,提出了一种基于受端换流站无功配置的高低端换流器电压分配策略。该策略采用VSC换流站和交流滤波器共同提供无功支撑的方案,通过建立VSC换流站额定容量和LCC额定功率的函数关系式,并结合交流滤波器配置容量和系统参数,推算出特高压混合直流输电系统中受端VSC换流器的最佳额定容量值,进而确定LCC和VSC换流器的电压配置结果;接着,在PSCAD软件中构建特高压混合直流输电系统和常规特高压站直流输电系统的电磁暂态模型。最后,通过稳态和暂态两种场景仿真验证了该系统及其电压分配策略的有效性。
1 特高压高压直流输电工程柔性化改造
1.1 受端串联型混合直流输电系统拓扑
目前国内投入运行的常规直流工程多采用双极大地回线方式[19],逆变侧柔性化改造后的拓扑结构如图1所示。其中,送端LCC采用双12脉动换流器,受端MMC的正负极分别通过直流母线引出直流联络线,连接到逆变侧LCC低压出线端和原接地极,通过串联形式即可实现受端换流器的柔性化改造。
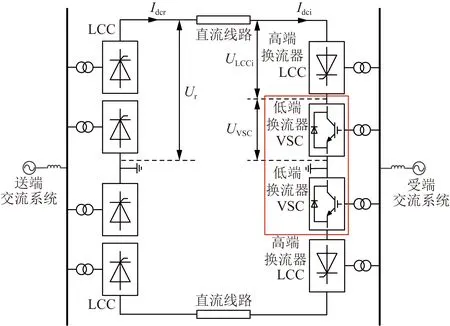
图1 受端串联型混合直流输电系统结构示意图Fig.1 Structure scheme of receiving-end series hybrid HVDC system
1.2 运行原理与数学模型
根据电路原理,设直流线路的等效电阻为R,则正极直流电压关系为:
Ur=ULCCi+UVSC+RId
(1)
式中:直流电流Id由送端LCC换流器的定电流方式决定;Ur为送端直流电压;受端LCC和VSC换流器的直流电压ULCCi和UVSC分别由各自的电压控制器决定,考虑线路压降后,送端电压即由ULCCi和UVSC的大小决定。
在稳态运行中,如果受端的直流电压指令保持不变,那么受端直流电压Udi基本保持恒定,受端各换流器的有功功率保持稳定;如果受端的直流电压指令发生变化,同时受端LCC的直流电压保持不变,那么直流输送功率的变化部分由VSC进行支撑或下调。
记Udi的变化量为ΔUdc,受端VSC接收的直流功率变化量ΔPVSC为:
ΔPVSC= ΔUdc·Id
(2)
送端LCC的直流功率变化量ΔPLCCi为:
ΔPLCCi=ΔPVSC= ΔUdc·Id
(3)
由此可知,该拓扑能够保证系统快速响应直流电压指令,充分发挥VSC换流器功率调节灵活、对电网冲击小的优点,通过VSC换流站即可获得功率/电压调节支撑,避免LCC换流器触发角频繁调节而造成的功率/电压冲击,有利于维持受端系统的稳定。
2 基于受端换流站无功配置的高低端换流器电压分配策略
2.1 受端换流站无功功率需求计算
直流系统LCC换流站的无功功率消耗量通常考虑系统的换相电抗和运行工况[20],单个受端LCC换流站的有功功率、无功需求可根据式(4)—(7)计算。
(4)
(5)
(6)
(7)
式中:PLCCi和QLCCi分别为受端单个LCC换流站的有功功率和无功功率;C为换流变压器参数;Ui为受端交流系统的母线电压;μ为换相角;γ为受端换流器的熄弧角;Xc为每相换相电抗;Id为整个系统的直流电流;Udi为受端系统的直流电压;Udio为理想空载电压。
2.2 交流滤波器配置方案
常规直流系统的交流滤波器主要考虑以下6个因素:1)谐波限制水平;2)交流系统强弱;3)滤波器容量;4)外部环境条件;5)系统控制方式;6)直流输电工程可靠性及设备可用率要求等。
一般而言,交流滤波器包括调谐滤波器和阻尼滤波器两种。调谐滤波器包括单调谐、双调谐和三调谐滤波器;阻尼滤波器包括单调谐、双调谐和三调谐阻尼滤波器。目前工程多采用阻尼滤波器,图2即为3种滤波器的电路图。

图2 典型交流滤波器电路图Fig.2 Circuit diagram of typical AC filters
根据文献[21]的优化分析结果,向家坝—上海直流工程的受端换流站采用交流滤波器的型式为11/13双调谐高通型滤波器、3/24/36三调谐高通型滤波器和并联电容器(SC)的组合滤波方案,受端需配置上述3种滤波器以满足谐波抑制和无功补偿的需求。
为充分挖掘VSC换流器的无功支撑能力,本文考虑交流滤波器和VSC共同提供无功的方案。对于受端单极系统,交流滤波器设置双调谐、三调谐、SC的组数均为1组,即满足基本的谐波抑制要求和补偿部分LCC换流器的无功功率需求,而LCC换流器剩余的无功功率需求则由VSC换流器来满足。本文所研究的混合直流系统参照向家坝—上海工程,故受端交流母线的额定电压设为500 kV。
忽略电阻的影响,设滤波器所要抑止的谐波次数为Ni,母线基波电压为Ufi,流过滤波器的基波电流为Ifi,滤波器电容为Cfi、电感为Lfi,则单调谐滤波器输出的无功功率Qfi如式(8)所示[22]。
(8)
式中ω为角频率。
由此可知,滤波器输出的无功功率与所连交流系统母线电压的平方成正比。以单极系统为例,每组容量为260 Mvar,设置的3组滤波器输出无功功率Qf为:
Qf=260×3=780 Mvar
(9)
2.3 高低端换流器电压分配策略
考虑到柔性化改造的投资成本,需要在受端串联的LCC和VSC换流器之间寻找一个适合的电压比例。确定电压比例的关键要素是优化系统总费用,作为换流站的核心设备,VSC换流器价格明显高于LCC换流器,需要将VSC额定容量作为柔性化改造工程成本控制的主要目标。因此,本文从VSC换流器额定容量入手,建立了VSC换流器容量关于LCC换流器额定功率的函数。根据高压直流输电送端系统的额定功率(Porder)、受端换流站总功率(Porderi)和逆变侧LCC换流器的额定功率(PLCCi),可得到VSC换流器的额定功率PVSC为:
(10)
VSC换流器所需产生的无功功率QVSC为:
QVSC=k·PLCCi-Qf
(11)
式中k为LCC变换器的无功功率需求与受端换流站总功率的比例,并且这部分无功功率需求应由交流滤波器和VSC共同满足。
基于上述分析,VSC换流器的额定容量为:
(12)
根据文献[23],将式(10)—(11)代入式(12),则:
(13)
为获得最佳的高低换流器电压配比,需要对价格相对昂贵的VSC换流器进行成本最小化处理,故可通过将VSC额定容量对LCC额定功率的导数设为零,进而计算出VSC的最佳容量,即有:
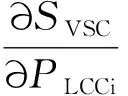
(14)
进一步可得LCC的最优额定功率PLCCi(opt)为:
(15)
因此,MMC的最优额定功率PVSC(opt)为:
(16)
根据该结果,能够确定合适的LCC和VSC额定功率比例。虽然LCC吸收的无功功率均可由VSC提供,但为了吸收LCC所产生的谐波,仍需设置滤波器(Qf≠0)。在额定工况时,送端LCC换流站所需的无功功率约为直流功率的30%~50%,受端LCC换流器约为40%~60%。由式(11)算得k=56%,按照最大无功功率需求设定k=60%。根据上文算得的Qf值,并设单极系统的额定功率Porder=3 200 MW。考虑线路压差,取直流线路的等效电阻R为10.0 Ω,可求得受端换流站总功率Porderi=3 040 MW,代入式(15)—(16),可确定高低端换流器LCC和VSC的额定功率分别为2 579.4 MW和460.6 MW。由于送端换流器整体的直流电压Uref为800 kV,额定直流电流为4 kA,可得高低端换流器电压ULCCiref和UVSCref分别如式(17)—(18)所示。
(17)
(18)
3 受端串联型系统的协调控制
送端LCC的控制目标是系统直流电流,采用定直流电流控制,并配置最小触发角限制(5 °)和低压限流控制(VDCOL),控制逻辑如图3所示。系统采集直流电压Ud和直流电流Id,Ud经过低压限流环节后直流电流的参考值Idref进行比较,其中较小的电流值将作为送端换流器的实际指令,该指令与Id产生的偏差值通过PI调节器后,再与π作差便可得到送端的触发延迟角αr。

图3 送端LCC定电流控制框图Fig.3 Block diagram of constant current control of sending-end LCC
受端LCC的控制目标是直流电压,采用定直流电压控制和定γ角控制方式,具体控制逻辑如图4所示。受端LCC实际电压值ULCCi与电压指令ULCCiref作差后得到偏差值,该偏差值与超前熄弧角γ二者取较大值,然后通过PI调节器产生逆变器的触发超前角β。根据β与α的关系,即可得到的延迟触发角αi。
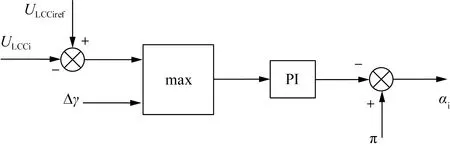
图4 受端LCC定电压控制框图Fig.4 Block diagram of constant voltage control of receiving-end LCC
逆变侧VSC有两个控制目标,采用定直流电压和定无功功率控制,控制逻辑图如图5所示。采用内外环控制方式,外环控制器将VSC的实际值UVSC与直流电压指令UVSCref作差后经过PI环节,通过计算得到内环控制器的d轴电流参考值,进而控制直流电压;同理,内环控制器的q轴分量也由外环提供,但其用来控制无功变量。

图5 受端VSC定电压控制框图Fig.5 Block diagram of constant voltage control of receiving-end VSC
基于上述分析,建立整个串联型混合直流输电系统的控制框图如图6所示。送端的LCC控制系统的直流电流,受端的LCC和MMC共同控制系统的直流电压。其中,LCC和MMC的额定电压ULCCiref和UVSCref由高低端换流器功率分配控制器给定。

图6 整个系统的协调控制框图Fig.6 Coordination control diagram of the total system
4 仿真与分析
基于±800 kV向家坝-上海特高压直流输电工程,本文考虑常规换流器和柔性换流器在电压等级和传输容量上的不匹配,额定直流功率设置为6 400 MW,额定电压为±800 kV,故额定电流为4 kA。由于双极系统对称运行,故以单极系统为对象建立电磁暂态模型,场景包括稳态运行和故障运行两种情况。特高压混合直流输电系统主要参数的具体设置如表1所示。
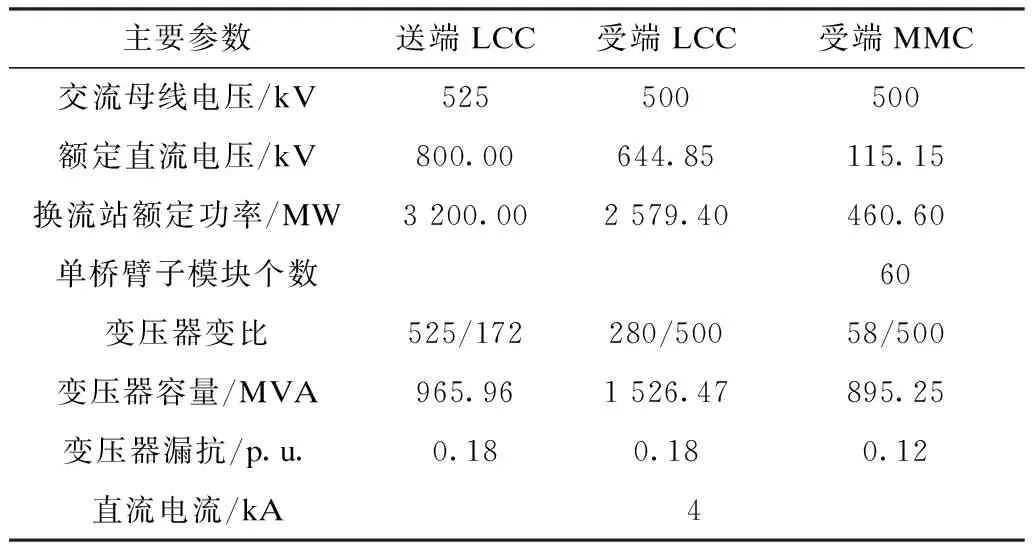
表1 串联型特高压混合直流输电系统的主要参数Tab.1 Main parameters of series hybrid UHVDC system
4.1 稳态响应特性
为便于PSCAD电磁暂态模型搭建,换流站所连交流系统均采用等值模型,通过恒压源表示交流电网,等值阻抗反应交流系统的强弱程度。控制策略如前文所述,设置稳态仿真时间5 s。系统输送功率、直流电压、直流电流的仿真波形如图7所示。
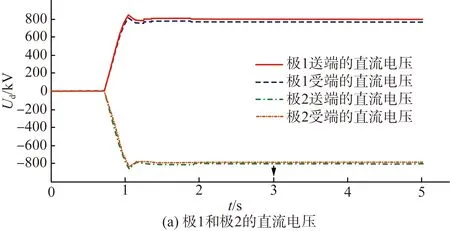
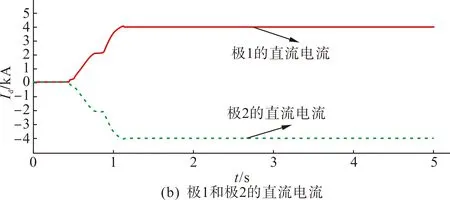
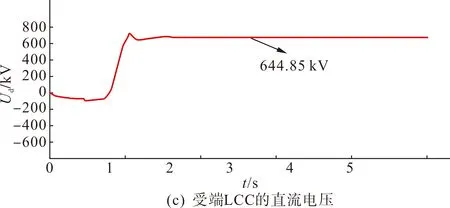
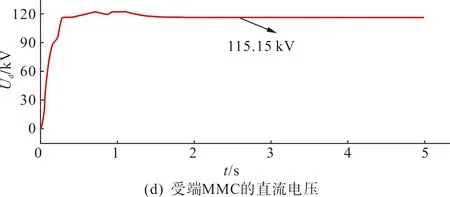
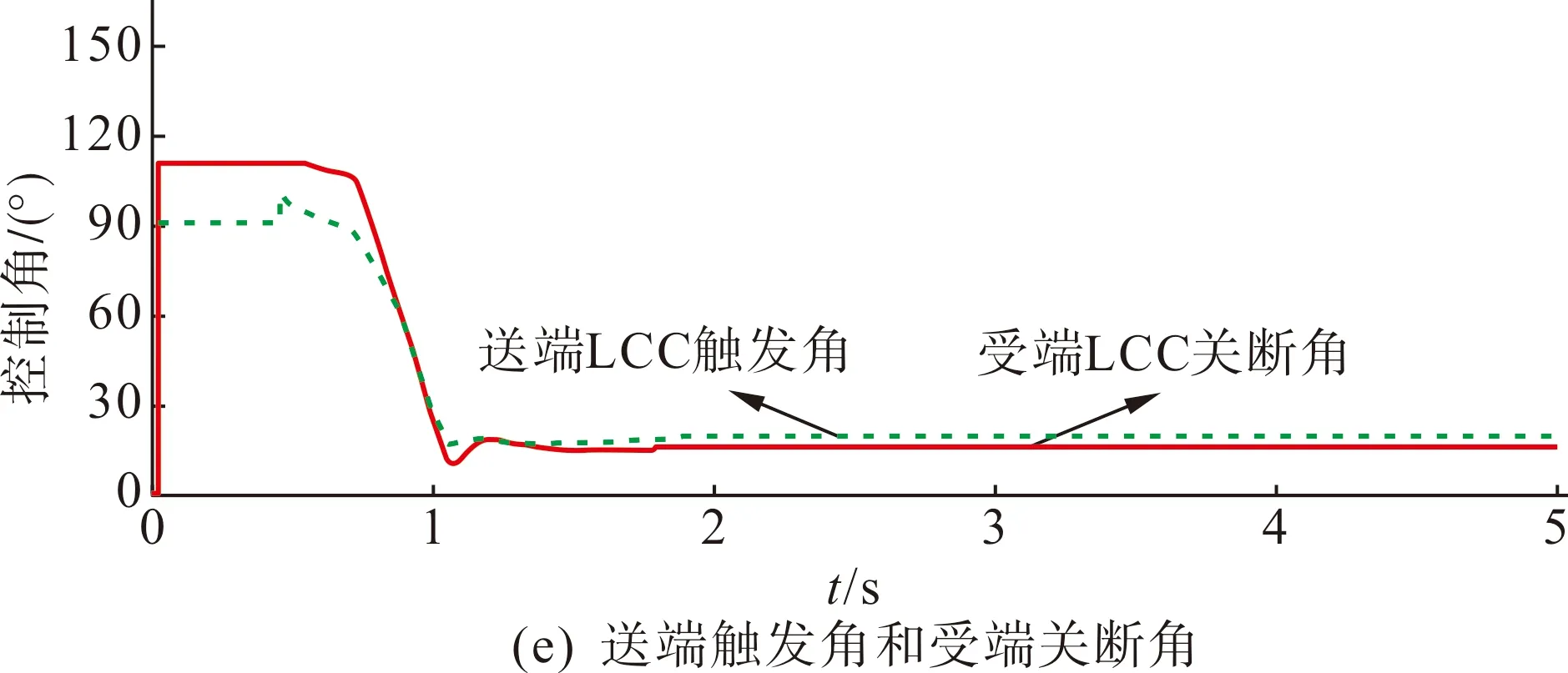

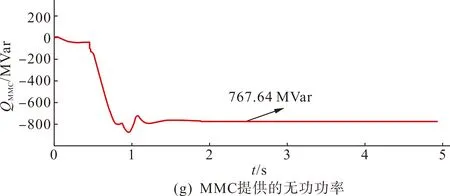
图7 系统的稳态响应特性Fig.7 Steady-state response characteristics of the system
由图7(a)—(b)可知,考虑线路压差后,特高压混合直流系统的送端和受端直流电压分别为800 kV和760 kV,直流电流稳态时维持在4 kA,极1和极2对称运行,均符合系统指令的运行要求。图7(c)—(d)表明系统按照本文的高低端换流器电压分配策略对LCC和VSC进行电压分配,其直流电压分别为644.85 kV和115.15 kV。根据图7(e),送端LCC换流器的触发角约在1.32 s时达到稳定,维持在18.59 °;受端LCC换流器的关断角约在1.55 s达到稳定,维持在15.42 °。由图7(f) —(g)可知,受端换流站总功率为3 040 MW,VSC换流器提供的无功补偿量为767.64 Mvar,配合780 Mvar的交流滤波器,能够保证受端LCC换流器的无功需求。由此可知,特高压混合直流系统的各个参数量均能达到设定值下的稳定状态,仿真结果验证了所提受端换流器电压分配策略及协调控制的稳态特性。
4.2 暂态响应特性
为验证该系统应对交流系统故障的恢复能力,分别设置受端交流系统发生单相接地故障和三相短路故障,并给出电磁暂态仿真结果。
4.2.1 受端交流系统发生单相接地故障
设置受端的交流系统于2 s时发生单相接地故障,交流母线电压下降至432.8 kV,故障持续0.05 s,并对比常规特高压直流输电系统的运行特性,仿真波形如图8所示。
图8(a)—(b)为特高压混合直流输电系统的仿真模拟结果,而图8(c)—(f)为特高压混合直流输电系统与常规特高压直流系统的对比图。当受端交流系统在2 s时发生单相接地故障时,交流电压下降到438.8 kV,特高压混合直流输电系统的直流电压也随之下降。如图8(c)—(d)所示,常规特高压直流系统的直流电压跌至0,直流电流出现短时的突增后开始下跌,约0.32 s后系统恢复稳定;相比于常规特高压直流的直流电压跌至0的情况,特高压混合直流输电系统的直流电压仅跌至638.4 kV,直流电流恢复更快,因而其抗扰动能力更强。图8(e)—(f)展示了特高压混合直流输电系统与常规特高压直流系统的触发角、关断角曲线,前者触发角的抬升幅度小于后者,后者的关断角在单相接地故障期间跌至零,并且图8(c)中直流电压跌至0,因而判定常规特高压直流发生换相失败,而特高压混合直流输电系统并未出现晶闸管换相失败的情况。因此,受端换流站在LCC与MMC串联的情况下,系统的换相失败抵御能力得到有效提升。



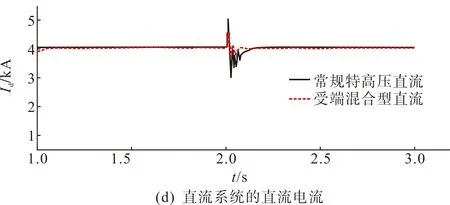


图8 受端交流系统单相接地故障时的暂态特性Fig.8 Transient characteristics of receiving-end AC system with single phase to ground fault
4.2.2 受端交流系统发生三相短路故障
设置受端的交流系统于2 s时发生三相短路故障,交流母线电压下降约20%,故障持续0.05 s,并对比常规特高压直流输电系统的运行特性,仿真波形如图9所示。
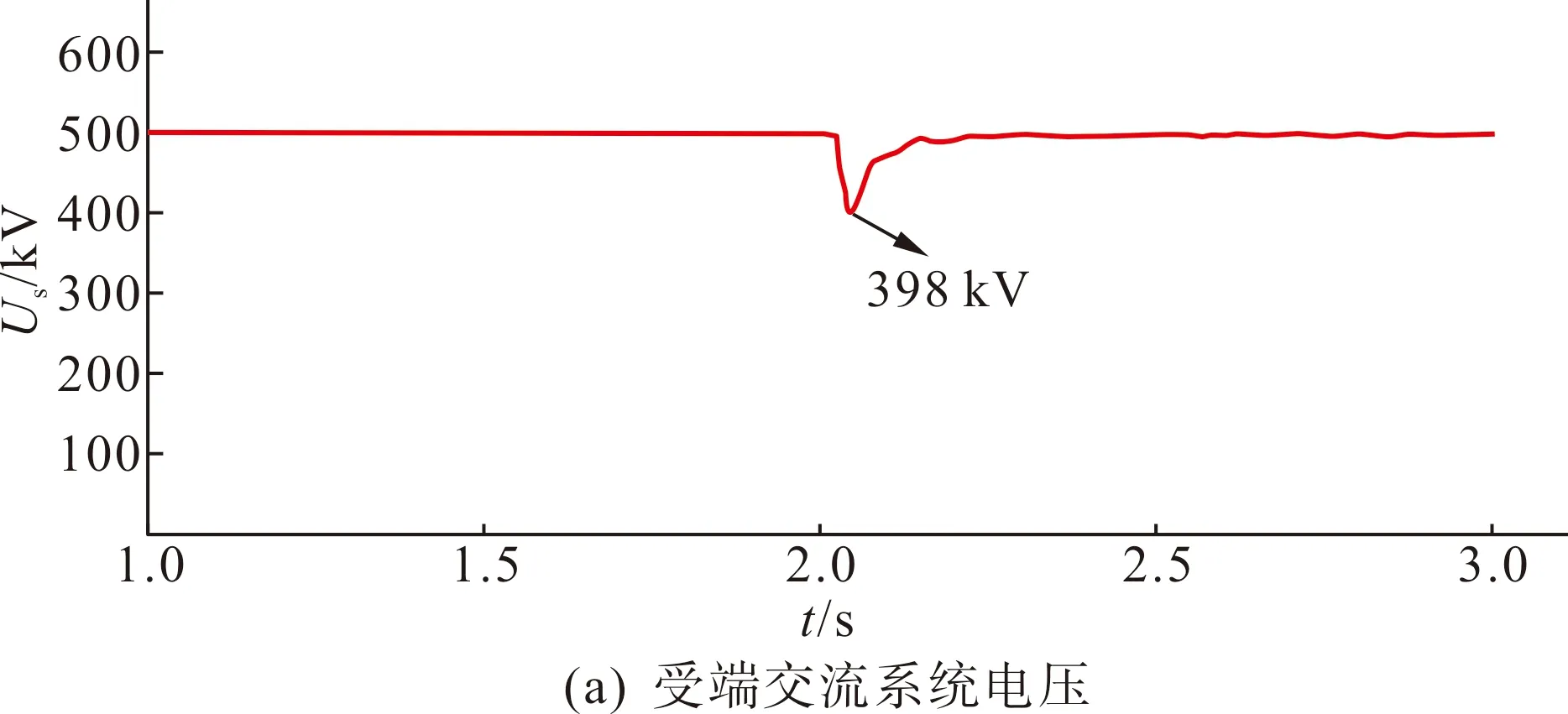

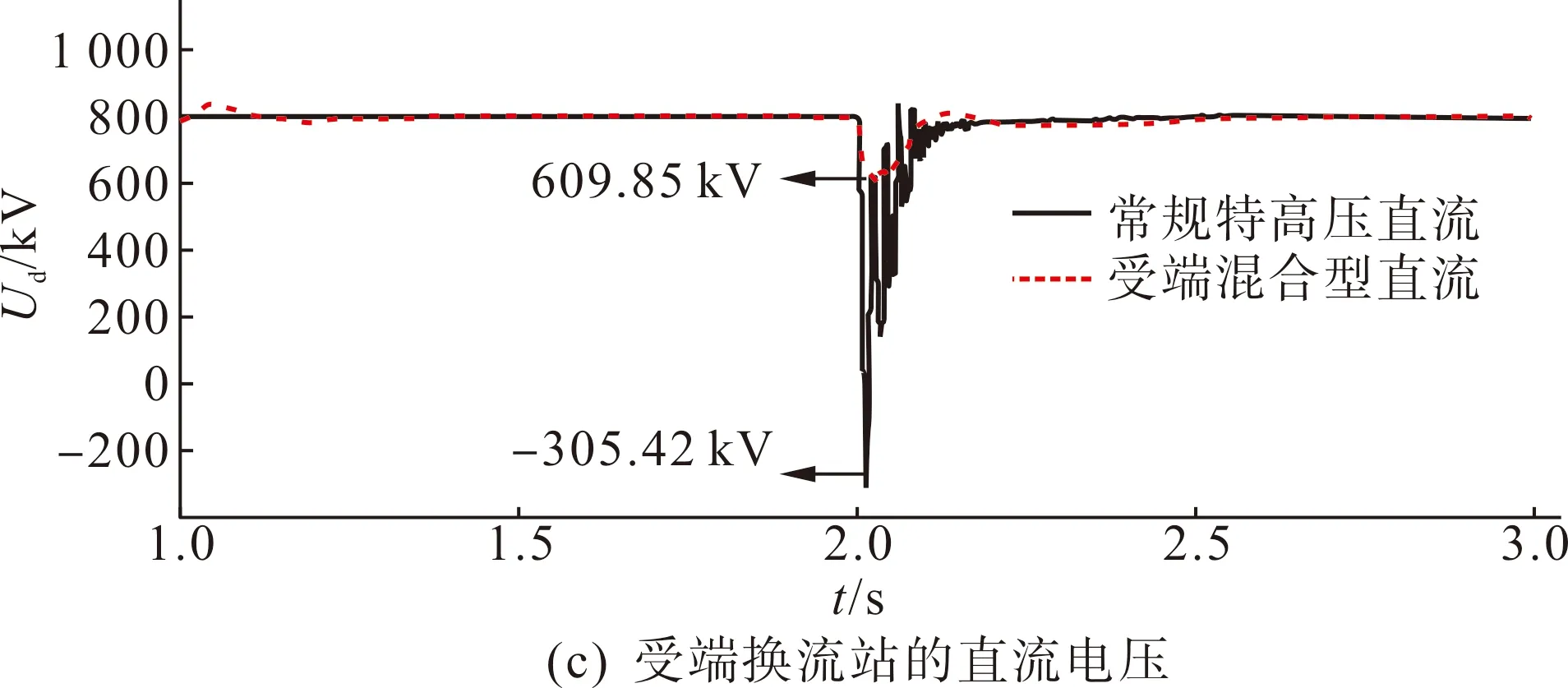

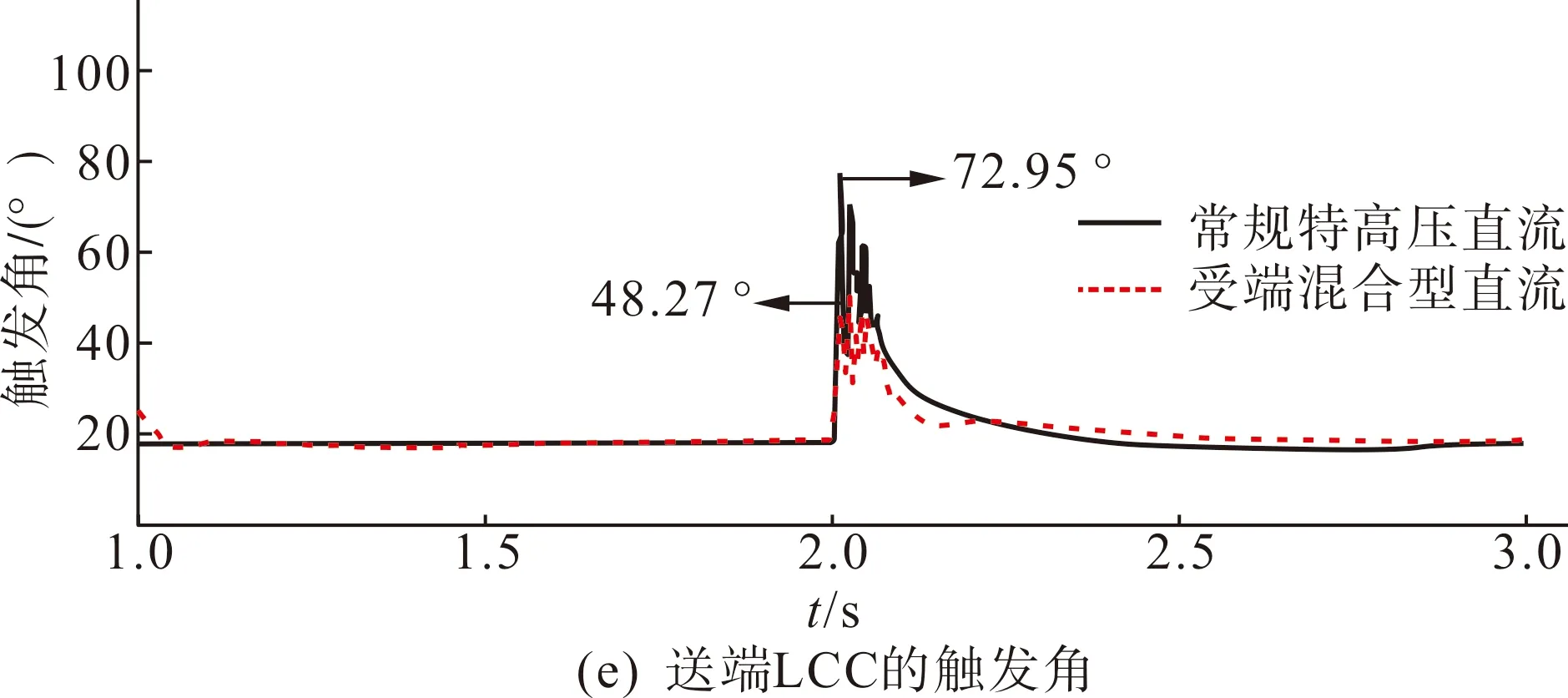
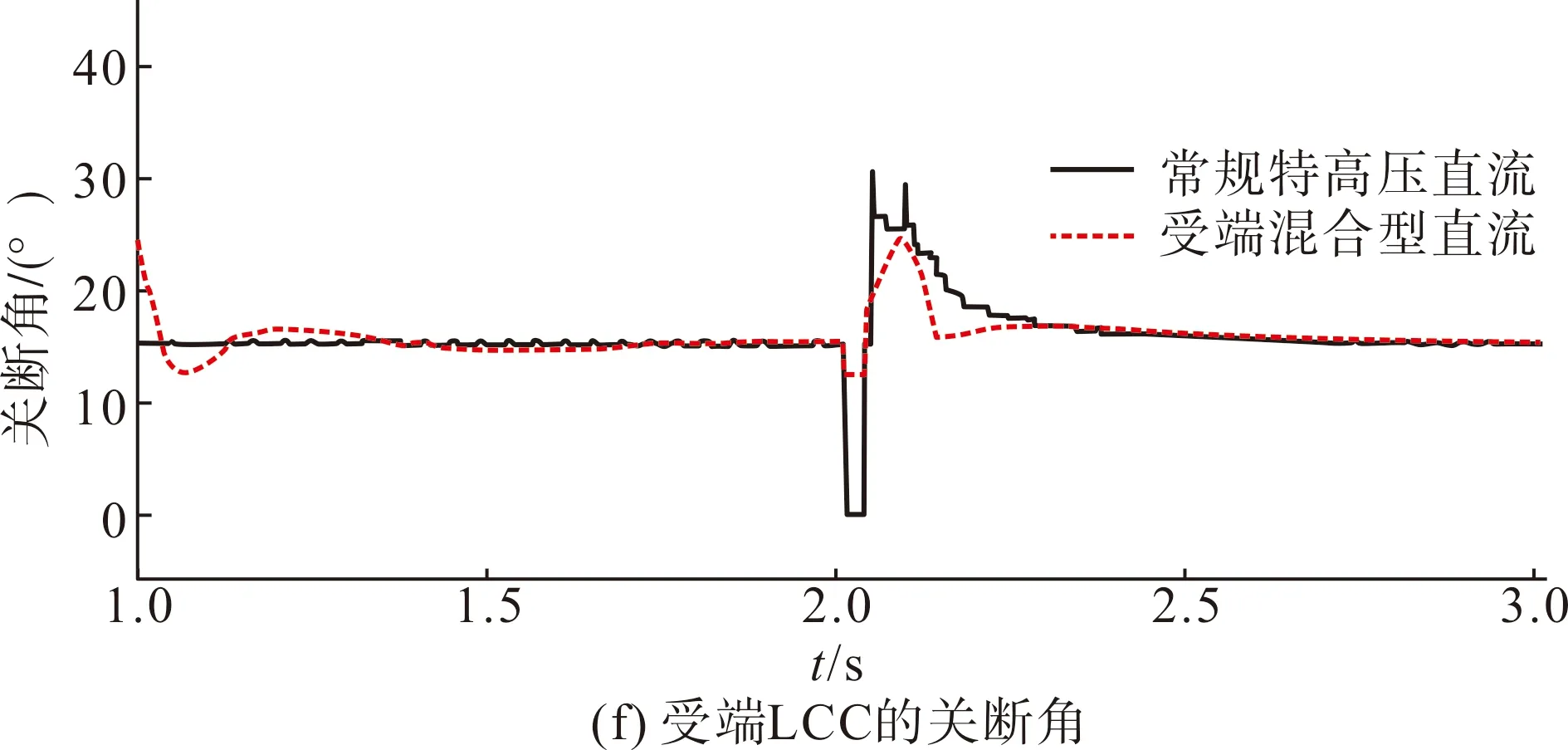
图9 受端交流系统三相短路故障时的暂态特性Fig.9 Transient characteristics of receiving-end AC system with three-phase short circuit fault
图9分别给出了特高压混合直流和常规特高压直流模型在受端电网发生三相短路故障时的暂态响应特性。根据图9(a),受端交流母线电压由原先的500 kV降至398 kV(约80%),交流电压约在3.25 s时恢复正常。由图9(b)可知,受端LCC换流器最多跌至482.75 kV,而VSC换流器则因具备较好的电压支撑能力,其两端的直流电压不减反增,最高达到127.1 kV,一定程度上减少了直流系统整体直流电压的跌落幅度,对系统直流电压起到了支撑作用。
如图9(c)—(d)所示,故障发生时,两个系统的直流电压和直流电流均发生迅速跌落,特高压混合直流系统的直流电压下跌程度较小,约为609.85 kV,而常规特高压直流则跌至零以下。两个系统的直流电流均有短时的小幅度上升,但随后便发生跌落。根据图9(e)—(f),两个系统的触发角在故障期间均有较大幅度的增加,常规特高压直流的触发角下降至0,说明其发生了换相失败。常规特高压直流系统在换相失败期间,由于关断角下降到0,受端LCC换流器由定电压控制转为定关断角控制,以此来限制系统的直流电流。在送端定电流控制与受端定关断角控制的配合作用下,直流电压和直流电流逐渐上升,关断角也随之上升,系统结束换相失败。由于特高压混合直流系统低端VSC换流器的快速电压支撑能力,高端LCC换流器的关断角在故障期间仅下降至12.76 °,系统未发生换相失败,一定程度上提升了LCC换相失败抵御能力。因此,本文所建立的特高压混合直流输电系统具备换相失败抑制能力,电压分配策略通过优化VSC换流器的额定容量,在满足受端LCC无功需求的同时,还保留了一定量的有功裕度,保证了直流系统的故障穿越能力。
5 结语
本文针对特高压混合直流输电系统中串联换流器的额定电压比例问题,提出了一种基于受端无功配置的高低端换流器电压分配策略,主要结论如下。
对常规特高压直流系统进行低端换流器柔性化改造,使其形成受端LCC和VSC串联型式的特高压混合直流拓扑,相比于受端全部柔性化改造方案,节约工程造价的同时也能解决常规直流换相失败困扰。
基于受端无功配置的高低端换流器电压分配策略综合考虑了VSC换流站和交流滤波器共同提供系统无功支撑的方案,通过建立VSC额定容量与LCC额定功率的函数关系式,优化获得LCC和VSC换流器的电压分配结果。当受端交流系统发生故障时,VSC换流器能够在LCC换流器无功需求减少的同时降低其无功输出,腾出一定的有功输出空间。同时,VSC能够灵活提升自身的直流电压水平以缓解系统直流电压的整体下跌幅度,从而保证系统直流电压的稳定。

