基于区间算法的直流输电系统元件可靠性参数求解模型

李凌飞，侯婷，李岩，姬煜轲，黄莹，辛清明，傅闯，李欢

(直流输电技术国家重点实验室(南方电网科学研究院)，广州 510663)

0 引言

高压直流 (high voltage direct current transmission, HVDC) 输电系统可靠性是指HVDC系统在一定时期内可靠输送电能的能力。HVDC系统传输容量很大，一旦发生故障会造成巨大损失，因此，准确量化HVDC系统的可靠性有很大的实际意义。

在直流输电工程规划时，一般需要计算规划方案的可靠性，以评估方案是否达到预定的可靠性要求，进而选择扩建或加固措施。通常可靠性评估根据拓扑结构、元件可靠性参数(故障率和修复时间)等来估算系统可靠性指标[1-3]。但是，元件可靠性参数通常从历史故障统计数据中获得，因此，这些数据往往会受到多种不确定性的影响[4]，目前主要表现在以下3个方面[5]：1) 电力系统中涉及海量统计数据，难免存在无效记录或数据缺失；2) 元件可靠性参数随着设备老化会发生变化，若数据更新不及时，会导致可靠性参数不准确；3) 部分场合下人工手动录入可靠性参数，但人员素质参差不齐，导致可靠性参数不准确。

对于HVDC系统来说，元件可靠性参数的选取直接影响HVDC系统可靠性评估的准确性，甚至影响规划的直流输电系统的可靠安全运行[6-7]。另外，对于电网公司而言，错误的可靠性评估结果也可能会误导直流输电设备的招标[8]。因此，获得准确的元件可靠性参数是进行可靠性评估的关键问题。

目前，国内外学者根据可靠性指标对元件参数的求取和校正已经做了一些研究。

针对大电力系统，文献[9]运用元件可靠性参数和可靠性指标之间的多重共线性关系，采用偏最小二乘回归求取原始可靠性参数，但没有建立可靠性参数和指标之间的数学表达式。文献[10]针对发电系统，运用多元非线性回归模型，建立了元件可靠性参数和可靠性指标的关系，但没有建立可靠性参数和指标之间的函数关系。文献[11]推导了发输电系统可靠性指标与可靠性参数之间的数学表达式，可以直观看到可靠性参数随可靠性指标的变化情况。文献[12]建立了电力系统可靠性评估逆问题的解析模型，并将其表示为非线性代数方程组，提出了一种基于区间二分消去法的Krawczyk算子改进算法，克服了在求解过程中选择合适初始区间的困难。

针对配电网，文献[13]提出了辐射状配电系统的逆可靠性评估问题，从已知的系统可靠性指标中寻找未知元件的参数。为此，提出并求解了一个非线性方程组。文献[14]提出可靠性指标的不确定性评估通常是通过故障率和修复时间中不确定性的传播来进行的，利用基于故障模式后果分析法的配电网可靠性评估模型，建立可靠性参数与可靠性指标映射关系的可靠性参数求解校正模型。

随着技术水平的提高，HVDC系统的可靠性指标统计相对准确，通常在系统运行参数、电气参数及结构等确定后，可以认为元件可靠性参数和系统可靠性指标间具有一一对应的关系[5]。采用可靠性指标求取元件的可靠性参数是一条有效的途径。然而，鲜有文献报道通过HVDC系统的可靠性指标求取元件参数的研究。文献[15]基于可靠性指标随可靠性参数单调递增的规律，建立了可靠性最优分解的非线性模型，运用二分法求解了可靠性最优分解问题，然而，该文献在求解中为简化计算，设定各元件可靠性按照同一比例变化，这显然不符合实际。文献[16]在可靠性最优分解的基础上，以投资成本最小为目标，从可靠性指标出发，求解可行的元件可用率，从而确定设备选型，达到投资成本最小的目标。文献[17]建立了元件对直流输电系统可靠性的最优分解模型，采用二分法求解，并开发出了直流输电系统可靠性评估平台。

由上述文献可以看出，关于HVDC系统由可靠性指标求取元件可靠性参数的一般性研究相对较少。而且，根据HVDC系统可靠性指标求取元件可靠性参数的已有文献所采取方法的精度有待提高：前述文献有关大电力系统和配电网等的元件可靠性参数求取的研究中，采取的算法主要分为经典数学规划算法和智能优化算法两类。数学规划算法包括内点法、信赖域反射法等，该类方法非常依赖于良好的初始解，否则只能收敛于局部最优；然而，元件可靠性参数可能的取值范围较宽，难以给出良好的初值解；智能优化算法的精度难以满足要求，且面临陷入局部最优的难题。因此，针对HVDC系统，本文利用全概率公式建立了可靠性指标关于待求元件的解析表达式，基于此提出了由可靠性指标求取元件可靠性参数的解析求解模型，采用基于初始区间二分排除和Krawczyk-Hansen算子的求解算法，在一个较大的可靠性参数初始取值区间内，该方法可以得到所有元件可靠性参数的精确区间解。本文所提出的模型实现了可靠性指标关于元件可靠性参数的解析表达，采用的求解算法避免了前述提到的优化算法陷入局部最优的缺点。最后，本文采用双12脉动接线HVDC系统进行了算例分析，证明了本文所提模型和算法可以准确求取元件可靠性参数。

1 高压直流输电系统可靠性评估模型

1.1 高压直流输电系统子系统划分

HVDC系统中包含海量数目的元件，若直接对所有元件抽样，会使得可靠性评估具有极大的挑战性[18]。因此，为降低计算复杂性，本文根据HVDC系统的特点，采用分而治之的方案，将HVDC系统划分为多个子系统。

本文以图1所示的双12脉动接线HVDC系统单线图为例进行建模分析。该系统由换流变压器子系统、交流滤波器子系统、直流输电线路子系统、阀组子系统、直流场子系统组成。下面分别建立各子系统的可靠性评估模型。本文首先假设不考虑换流变压器备用和平波电抗器备用的影响。

1.2 高压直流输电系统子系统可靠性模型

1.2.1 换流变压器子系统

图1中，a模块代表换流变压器子系统。由a模块可知：

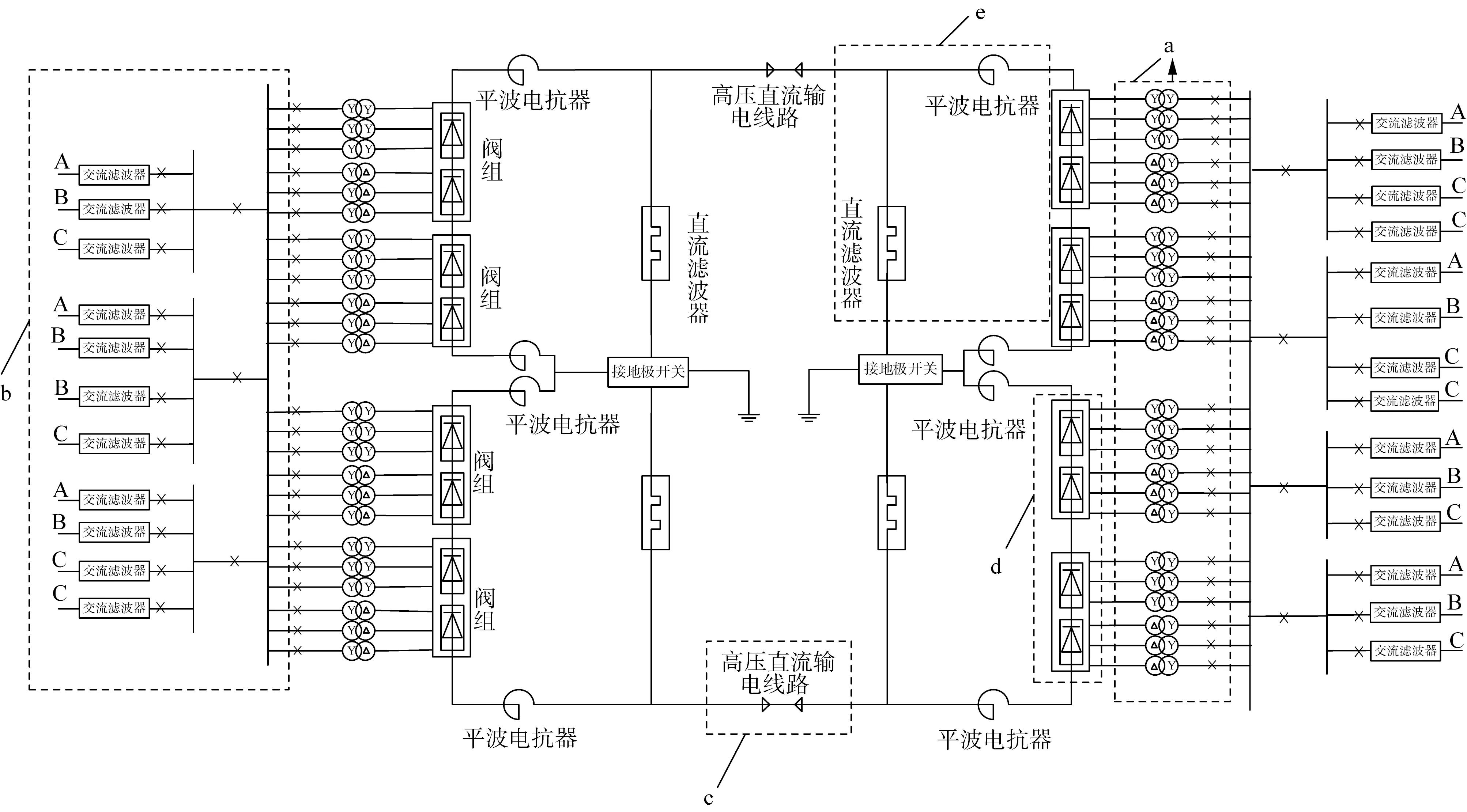
图1 双12脉动接线高压直流输电系统子系统划分示意图Fig.1 Sketch diagram for subsystem division of HVDC transmission system with double twelve pulse arrangement

1)换流变压器子系统在每一极上均有12台换流变压器，其中Y/Y、Y/△接线各6台；

2)每个换流阀与不同接线的换流变相连，其中Y/Y、Y/△接线各3台；

因此，典型元件组停运为单个12脉动换流阀对应的6台换流变停运[8]，不能直接将换流变压器子系统等效为多状态元件进行可靠性评估，本文采用简化等值方法解决这一问题，考虑到可能计及变压器备用的影响，本文分别将每个换流阀对应的3台Y/Y与3台Y/△接线的换流变压器等效为1个元件。

由a模块可知，每个换流阀对应的3台Y/Y与3台Y/△接线的换流变压器之间为串联结构，根据串联结构的故障率和修复率等值公式，可得到等值元件故障率和等值修复率，分别如式(1)—(2)所示。

(1)

(2)

式中：n为元件个数，此处取6；c为换流变接线方式，Y/Y型或Y/△型；λi_c和μi_c分别为第i个Y/Y或Y/△型接线换流变压器的故障率和修复率；λt_c和μt_c分别为一个换流阀对应的换流变压器的等值故障率和修复率。

1.2.2 交流滤波器子系统

图1中，b模块代表交流滤波器子系统，交流滤波器子系统结构如图2所示。由图2可知：交流滤波器子系统元件较多，主要包括主母线、小母线、断路器和交流滤波器；结构相对复杂，但交流滤波是串联关系，因此，可以根据式(1)、式(2)等效为主母线、小母线、交流滤波器3类元件。但是，实际工程中，往往会投入不同类型和型号的交流滤波器，因此，需要确定交流滤波器子系统的容量状态，本文采用容量状态表，介绍如下。

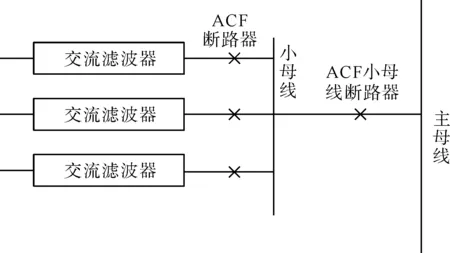
图2 交流滤波器子系统结构图Fig.2 Structure diagram of AC filter subsystem

假设有4类交流滤波器，分别用F1、F2、F3、F4表示；各类别数量记为N1、N2、N3、N4。则本文定义投运等效值表示为：Seq=(N1×1 000+N2×100+N3×10+N4×1)，投运等效值和容量状态一一对应，各种投运情形下的容量状态都可以通过投运等效值来确定。如F1型交流滤波器故障后，系统等效投运值Seq1=Seq-1 000，再根据投运等值表即可确定系统容量状态。

1.2.3 直流输电线路子系统

图1中，c模块代表直流输电线路子系统，其中元件主要为高压直流输电线路，因此可直接等效为两状态元件。

1.2.4 阀组子系统

图1中，d模块代表阀组子系统，它包括同一极的2个12脉动换流阀组，其中每一个12脉动阀组由2个6脉动阀串联。因此，根据式(1)—(2)可以将每个12脉动阀组等效为两状态元件。两个12脉动阀组间为可靠性上的并联关系，即任一阀组故障只会导致相应极失去50%的容量。

1.2.5 直流场子系统

图1中，e模块代表直流场子系统，其中主要元件为直流滤波器和平波电抗器，2个元件任一个故障均会导致该极停运，因此二者为串联关系，可以根据式(1)—(2)等效为一个两状态元件。

1.3 高压直流输电系统可靠性指标

HVDC系统可靠性指标主要包括能量不可用率REU、能量可用率REA、系统期望传输容量PEC、单级计划停运次数FMPOT、单级强迫停运次数FMFOT、双极计划停运次数FBPOT等指标。本文主要选用REU、FMFOT和FBPOT指标进行分析，定义如下。

1)能量不可用率

(3)

(4)

TEOT(i)=Ti(1-停运期间可用容量÷PS)

(5)

式中：TS为系统时间尺度；TTEOT为TS内总等值停运时间；TEOT(i)为一年中第i次等值停运时间；N为总停运次数；PS为系统额定容量。

2)单极强迫停运次数

FMFOT指标定义为TS时间内HVDC发生单极强迫停运的次数。

3)双极强迫停运次数

FBFOT指标定义为TS时间内HVDC发生双极强迫停运的次数。

1.4 可靠性评估方法

传统的可靠性评估方法主要分为模拟法和解析法[19]。解析法主要是根据元件参数枚举状态求解可靠性指标，置信度高，但不适用于复杂系统；模拟法采用随机抽样模拟系统状态计算复杂适用于大规模系统，其主要方法为蒙特卡罗法。本文采用系统状态转移抽样法。

系统状态转移抽样法是对整个系统的状态转移进行抽样的一种序贯蒙特卡罗方法，重点是确定系统当前状态的持续时间以及系统的下一状态及持续时间。通过大量抽样，最后即可计算得到系统可靠性指标。具体步骤如下。

1)假定元件状态持续时间服从指数分布，并且初始时刻元件全正常。

2)根据式(6)计算系统状态持续时间Tk；

(6)

式中：m为当前状态向外转移情况总数；U为[0,1]间的随机数；λi为元件i的状态转移率。

3)根据式(7)计算元件j的状态转移概率Pj，并根据式(8)得到元件累积转移概率Pi。

(7)

(8)

4)根据式(8)进行元件状态转移定位，如果状态转移指标Ch=1，则元件发生状态转移，否则，元件状态保持不变；

Ch=find(Pi>rand(1))

(9)

5)得到一定数量的系统状态后，计算系统状态SState。

6)根据式(3)—(5)更新可靠性指标，并统计单极和双极强迫停运次数。

7)计算方差系数n，如式所示。若n小于一个常数(本文取0.002)，则停止迭代计算，输出相应的可靠性指标，否则，重复步骤2)—4)，生成新的系统状态。

(10)

式中T为时间尺度。

2 高压直流输电系统元件参数求解解析模型

2.1 元件可靠性参数求解分类

针对根据元件可靠性指标求解元件可靠性参数问题，可能存在以下3种情况：1)已知系统可靠性指标数量大于待求元件可靠性参数数量。2)已知系统可靠性指标数量等于待求元件可靠性参数数量。3)已知系统可靠性指标数量小于待求元件可靠性参数数量。本文仅介绍系统可靠性指标与待求元件可靠性参数数量相同的情况，该情况下方程有唯一解。

假设本文已知的HVDC系统可靠性指标为能量不可用率REU、单极强迫停运次数FMFOT和双极强迫停运次数FBFOT，待求的HVDC系统元件可靠性参数为元件的故障率和修复率。

2.2 考虑待求元件可靠性参数的可靠性指标解析模型

本文假设能量不可用率REU和单极强迫停运次数FMFOT、双极强迫停运次数FBFOT已知，元件1的故障率λ1和修复率μ1均未知，元件2的故障率λ2未知，元件3的修复率μ3未知，以此来推导元件可靠性参数求解模型。参数未知的元件个数为3，则这些元件状态的组合一共有23=8种情况，本文用X表示元件1、2、3的未知参数向量[λ1,μ1,λ2,μ3]，则REU、FMFOT、FBFOT具体推导过程如式(11)—(16)所示。

1)能量不可用率REU的解析模型推导如下。

式中：Ai、Ui(i=1,2,3)分别为稳态可用度和稳态不可用度，Ai=μi/(λi+μi)，Ui=λi/(λi+μi)；

(12)

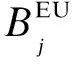
2)单极强迫停运次数FMFOT的解析模型推导如下。

(13)

其中，WiMFOT可表示为：

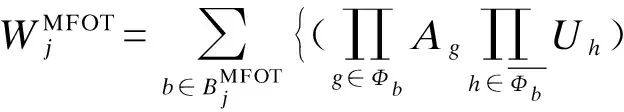
(14)

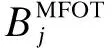
双极强迫停运次数FBFOT的解析模型推导如下。

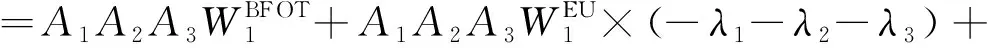
(15)

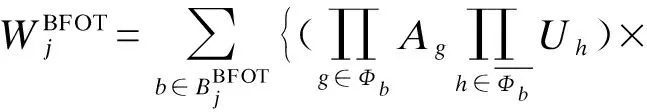
(16)

(17)

式(17)可简化为式(18)。

F(X)=0

(18)

下面重点解决如何求解非线性方程组式(18)，进而得到HVDC系统元件可靠性参数区间。

3 基于二分排除和Krawczyk-Hansen算子的区间算法的高压直流输电系统元件可靠性参数求解模型

针对式(17)或式(18)对应的非线性方程组进行求解，常用点迭代法，虽然该方法计算简单，但不能直接判断解的唯一性，除此之外，选取合适的初始值也是运用该方法的关键[21]。因此，为解决上述问题，本文提出采用基于初始区间二分排除和Krawczyk-Hansen算子的区间算法求解高压直流输电系统元件可靠性参数。

3.1 区间数与区间运算

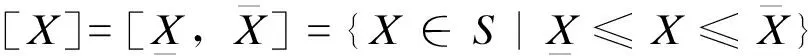
(19)

区间的四则运算定义为：

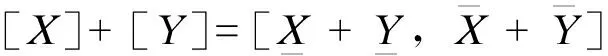
(20)

(21)

[X]×[Y]=[minS, maxS]

(22)

(23)

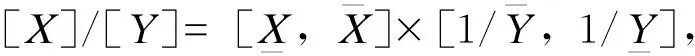
(24)

关于区间的其他运算可以参见文献[20]。

3.2 基于区间二分排除和Krawczyk-Hansen算子的非线性方程组求解的区间迭代法

Krawczyk-Moore算子是在区间Newton法的基础上发展起来的[21]，算法迭代公式如下。

K(y,X)=y-Yf(y)+[I-YF′(X)](X-y)

(25)

y=m(X)

(26)

Y=[m(F′(X))]-1

(27)

Hansen在迭代中改进Krawczyk-Moore算子，得到Krawczyk-Hansen算子：

H(y,X)=y-Yf(y)+L(X)(H′-y)+
U(X)(X-y)，y∈X

(28)

H′=H(y,X)∩X

(29)

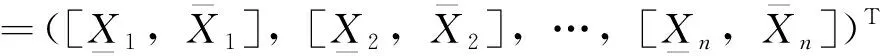
(30)

m(X)=(m(X1),m(X2),…，m(Xn))T

(31)

式中：X为区间向量；m(X)为区间向量X的中点；I为n阶单位矩阵；Y为n阶非奇异矩阵；L(X)和U(X)分别为区间矩阵[I-YF′(X)]的下三角矩阵和上三角矩阵。

当所研究的区间过大时，Krawczyk-Hansen算子往往无法有效判定该区间上是否存在解[22]，为了解决这个问题，本文采用二分排除缩小区间的宽度，使得Krawczyk-Hansen算子能够判定细分区间上解的情况。

因此，基于区间二分排除和Krawczyk-Hansen算子的非线性方程组求解的区间迭代法算法流程如下。

1)令[X]=[X]0∈I(Rn)， 初始化二分区间表B， 解区间表T。初始化二分变量序号b=1、二分区间表长度l=1，给定解区间的收敛精度ε和ξ， 初始化区间宽度系数α。

2)根据Krawczyk-Hansen算式(28)—(31)计算H(X)和Z=X∩H(X)。

3)根据Z和X的包含关系判断解的存在性和唯一性。若Z=Ø，则转流程6)；若W(X)属于X，则在X上有解，转流程4)；若W(Z)<αW(X)，则X=Z，转流程2)；否则，转流程5)。

4)以m(X)为初值，利用点Newton法迭代计算，可得方程组的一个解X*，并存入表T。

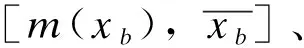
6)若l=0，则转流程7)。从区间表B取出排在首部的区间赋给X，l=l-1，转流程2)。

7)输出表T中的全部解区间。若T为空集，则该方程组无解。

4 算例分析

4.1 算例简介

本文以双12脉动接线的HVDC系统作为算例，进行可靠性评估分析。双12脉动接线的高压直流输电工程示意图如图1所示。逆变侧和整流侧共有24台换流变，4组阀组，还包含平波电抗器、交流滤波器等，其中，平波电抗器有3种型号。各元件原始参数如表1所示[1]，本文利用状态转移抽样法计算可靠性指标。并以该指标作为输入，利用本文的可靠性参数校正模型求解得到相应的可靠性参数。

表1 双12脉动接线特高压直流输电系统可靠性参数Tab.1 Reliability parameters of HVDC power transmission system with double twelve pulse connection

4.2 可靠性评估结果

本文采用状态转移抽样法计算双12脉动接线高压直流输电系统的状态停运容量，结果如表2所示，表中分别给出了各故障容量状态下的状态概率和频率指标。双12脉动接线高压直流输电系统可靠性指标计算结果如表3所示。

表2 双12脉动接线高压直流输电系统容量状态对应概率和频率计算结果Tab.2 Caculation results of probability and frequency of corresponding capacity of double twelve pulse HVDC

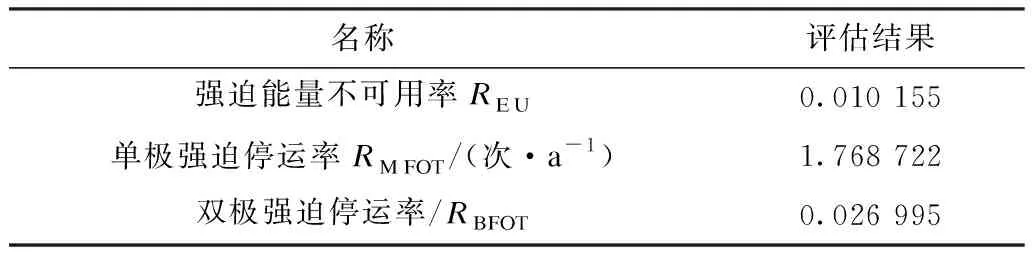
表3 双12脉动接线高压直流输电系统主要可靠性指标评估结果Tab.3 Assessment results of main reliability indexes of double twelve pulse HVDC power transmission system

从表3可以看出，双12脉动接线系统的可靠性比较高，这是由于双12脉动接线系统的单侧单极有4个换流单元，只故障1个换流单元并不会导致该极完全停运。

4.3 可靠性参数解析模型求解结果分析

以4.2节计算得到的REU、RMFOT和RBFOT指标作为已知参数，代入本文的基于初始区间二分排除和Krawczyk-Hansen算子的HVDC系统元件可靠性参数求解模型中，求解元件可靠性参数。

本文假设换流变压器、直流输电线和直流滤波器的故障率分别为λ1、λ2、λ3，修复率分别为μ1、μ2、μ3。将可靠性参数区间的最大值均放大为真实指标的2倍，最小值缩小为原来的1/2，下面设置4个算例来验证本文所提模型的正确性和有效性。

Case1：当强迫能量不可用率、单极强迫停运率、双极强迫停运率3个可靠性指标只有1个已知时，求取λ1、λ2、λ3、μ1、μ2、μ3中任意1个元件可靠性参数，求解结果如表4所示。

表4 Case1参数求解计算结果Tab.4 Calculation results of parameter solution in case 1

Case2：当强迫能量不可用率、单极强迫停运率、双极强迫停运率3个可靠性指标已知任意2个时，求取λ1、λ2、λ3、μ1、μ2、μ3中任意2个元件可靠性参数的组合，求解部分结果如表5所示。

表5 Case2参数求解计算结果Tab.5 Calculation results of parameter solution in case 2

Case3：当强迫能量不可用率、单极强迫停运率、双极强迫停运率3个可靠性指标均已知时，求取λ1、λ2、λ3、μ1、μ2、μ3中任意3个元件可靠性参数的组合，求解部分结果如表6所示。

表6 Case3参数求解计算结果Tab.6 Calculation results of parameter solution in case 3

Case4：当强迫能量不可用率、单极强迫停运率、双极强迫停运率3个可靠性指标均已知时，运用遗传算法求解λ1、λ2、λ3、μ1、μ2、μ3。结果如表7所示。

表7 Case4参数求解计算结果Tab.7 Calculation results of parameter solution in case 4

将表4—6的可靠性参数计算结果与表1中元件可靠性参数相比可知：无论是利用单个可靠性指标求解单个元件可靠性参数，还是利用多个可靠性指标求解元件可靠性参数的组合，本文提出的区间二分和Krawczyk-Hansen算子的区间算法计算得到的元件可靠性参数均被压缩在一个很小的取值区间内，并且包含表1中元件给出的可靠性参数，因此，表4—6的结果证明了所提算法能有效准确地求解出对应的元件可靠性参数。本文定义求解精度为参数解区间与真值的误差。经计算，各元件可靠性参数区间结果的精度均可以达到10-5，不同取值的同类型参数的求解结果达到了相似的精度，这说明求解精度与待求元件可靠性参数本身数值大小无关。同时，由表4—6可以发现，对于同一组待求的可靠性参数，采用不同的可靠性指标的组合，则求解得到的元件可靠性参数的精度不同。

表7为基于遗传算法求解方程得到的元件可靠性参数结果。比较表7结果和表1的参数给定值可以发现，遗传算法计算得到的结果存在显著误差。

以元件1的故障率和修复率为例：通过REU指标求解得到的元件1的故障率和修复率区间分别为[0.021 19, 0.021 21]、[65.779 99, 65.780 01]，最大相对误差分别为0.047 2%以及0.000 015 2%；通过REU和RMFOT计算得到的元件1的故障率和修复率分别为[0.021 19, 0.021 21]、[65.780 00, 65.780 01]，最大相对误差分别为0.047 2%以及0.000 015 2%；通过REU、RMFOT、RBFOT计算得到的元件1的故障率和修复率为[0.021 20,0.021 20]、[65.775 75, 65.785 90]，最大相对误差分别为0以及0. 008 97%。遗传算法求解得到的故障率为0.021 17，相对误差为2.12%，修复率为65.679 1，相对误差为0.153 4%。

通过上述计算的相对误差可以发现以下两点。

1)相对于Case1和Case2，已知系统可靠性指标数目为3(即Case 3)时，求解结果的误差比较大，这是因为Case3的情况有多个待求修复率，而强迫停运率指标关于修复率参数的灵敏度很小。针对待求元件可靠性参数中存在多个修复率时得求解精度会较差这种情况，可以有2种方法提高求解精度。

(1)给出可靠性参数的良好的初始取值区间；

(2)减小区间算法中设置的最小允许区间分割宽度。

2)相对于本文提出的区间二分和Krawczyk-Hansen算子的区间算法，基于遗传算法的元件可靠性参数求解结果的误差较大。这说明遗传算法容易陷入局部收敛，达不到全局最优。作为对比，本文所提模型能够得到包含元件可靠性参数真值的精确区间。

5 结论

本文首先采用状态转移抽样法对双12脉动接线高压直流输电系统进行可靠性评估。再基于可靠性参数与可靠性指标的映射关系，利用全概率公式推导了HVDC系统可靠性指标与元件可靠性参数之间的解析函数，最终建立了基于初始区间二分排除和Krawczyk-Hansen算子的HVDC系统的元件可靠性参数求解模型，对元件可靠性参数进行校正。

基于双12脉动接线的HVDC系统的测试验证了本文模型的正确性和有效性。计算结果表明，本文所提模型能够精确地求解得到HVDC系统主要元件的可靠性参数，而且求出的可靠性参数区间的误差要小于遗传算法的求解误差，解决了遗传算法依赖初始区间、求解精度不高的问题。