基于状态方程的高压直流换流器直流回路阻抗计算及直流谐振抑制
李欢,辛清明,傅闯,赵晓斌,许树楷
(直流输电技术国家重点实验室(南方电网科学研究院),广州510663)
0 引言
基于晶闸管半导体开关的十二脉动高压换流器因其通流能力强、容量高而普遍应用于高压直流输电[1]和直流融冰等领域[2-3],由于换流器中非线性晶闸管开关的存在,其直流回路中除了直流分量,还存在谐波电压分量,其在直流回路中会产生相应频率的谐波电流。当直流回路的谐波阻抗较低时,直流回路将有较大谐波电流,极端情况甚至会引发直流回路谐振,对交直流系统设备等将产生不利影响[4-5]。为避免产生直流谐振,高压直流换流器系统的直流回路阻抗值需满足一定设计要求,在敏感谐波频率附近的阻抗值不能太小,以保证系统安全稳定运行[6-8]。
高压换流器系统主要包括非线性的半导体晶闸管开关、换流变、交流电网、交流滤波器、直流线路、直流负载和控制系统等部分,其中每一部分都与系统直流谐波阻抗的值有关。当不考虑控制系统特性时,换流器的触发角认为恒定不变,然后基于该触发角可对换流器的直流阻抗进行稳态计算[9]。也有研究将换流器近似等效为一个电感,然后与直流出口的平波电抗器串联得到直流阻抗[10],这些方法没考虑控制系统等的影响,使用场景会受到一定限制。文献[11]通过电磁暂态仿真软件的仿真计算来获得系统的直流回路阻抗,该方法准确、直观可靠,在实际工程中也得到了较好应用,但对设计人员的工程经验要求较高。
在直流回路谐振抑制方面,目前的解决方法主要是改变系统主回路设备,如增加滤波器或阻波器等[12],从而提高系统直流回路在某些特定频率点的阻抗,该方法直观、可靠,对直流谐振可起到很好的抑制作用,在实际工程中也得到了很好的验证。
本文提出一种基于状态方程的高压直流换流器直流谐波阻抗计算方法,对换流器系统的晶闸管换流器、控制系统、直流负载、直流线路、换流变压器、交流滤波器、交流电网阻抗、交流电源等进行分析建模,建立了系统的状态方程,并推导得出了换流器直流回路谐波阻抗的状态空间解析表达式,形成了基于状态方程的高压换流器直流回路谐波阻抗计算方法,明确了直流谐波阻抗与晶闸管换流器、控制系统、直流负载、换流变、交流滤波器、交流电网阻抗等的内部逻辑数学关系,基于该数学关系可对直流谐波阻抗进行定向定量的调整和设计,实现直流谐振问题的主动灵活抑制,可省去阻波器等设备,节省设备的投资、占地和运维,显著提高系统的经济性和灵活性。
1 高压直流换流器系统
本文以单12脉动整流器为例进行研究,其典型系统框图如图1所示。

图1 高压直流整流器系统框图Fig.1 Block diagram of high voltage DC rectifier system
图1中包括6部分:交流滤波器为3组不同类型的滤波器并联,流入滤波器的总电流为IV;交流电源为戴维南等值电压源,Vs为交流侧电压源,其幅值为Vac,相位为θ0,Ls为交流电网等值电感,Rs为交流电网等值电阻,流过电网的交流电流为Is;换流变压器包括T1和T2两组理想变压器,其接线形式分别为Y-Y和Y-D接线,变比均为Kt:1,T1和T2的漏电感均为Lt,换流变网侧电压为Vp,换流变流入交流系统的电流为Ic;换流器由两组基于晶闸管开关的6脉动换流器串联组成,其中晶闸管为理想开关,不考虑其开关时间和缓冲回路;测量控制系统为基于负载直流电流的定电流反馈控制系统,直流电流为IDC,电流参考值为Iref,比例积分环节系数分别为Kp和Ki,α为换流器的触发角控制值;直流线路采用两组π形电路级联等效[13]。直流侧负载为电感L和电阻R串联,直流电压为Vdc。PLL为换流器交流侧电压的锁相环。
2 数学模型
晶闸管开关为高度非线性元件,高压换流器呈现非线性特性,难以直接得出系统线性化模型。本研究采用基于开关函数的小信号分析法来对换流器进行建模,换流器的状态方程建模方面,业界已有较多研究[14],相关研究目前主要关注系统的稳定特性分析,本文采用状态方程的方法主要用来建立换流器直流回路谐波阻抗的数学模型。换流器脉冲触发方式为等间隔触发,交流电压三相对称,直流电流为平滑直流,且只考三相开关函数傅里叶展开的基波分量[15-16],然后对交流三相变量进行dq变换,得到系统各变量的表达式如式(1)—(2)所示。
(1)
式中:μ为换相重叠角;θVp为母线电压初相位;φ1为功率因素角;θPLL为换流器母线电压Vp的相位;由锁相环根据Vp的dq分量进行闭环反馈计算得出。
12脉动换流器的直流输出电压为
(2)
式中Xt为换流变漏抗。定电流控制器采集到整流侧直流电流IDC后,首先经过测量环节,电流测量值Idcm与电流参考值Iref比较得到差值作为PI控制环节的输入,最后得到整流侧换流器触发角α。
整流侧定电流控制环节的状态方程如式(3)所示。
(3)
式中:x1为直流电流与参考值偏差量的时间积分量;T1为电流测量环节的时间常数;G1为测量增益。
整流侧换流器触发角表达式如式(4)所示。交流系统的dq坐标系内的状态方程如式(5)所示。
(4)
锁相环PLL的原理框图如图2所示。

图2 锁相环原理框图Fig.2 Block diagram of phase locked loop

(5)
式中:C1、C2、C3、C4、R1、R2、R3、L1、L2分别为交流滤波器的电容、电阻和电感参数;ωr为PLL锁相环的输出相位变化角速度;Vpd、Vpq、Vc2d、Vc2q、Vc3d、Vc3q、Vc4d、Vc4q、IL1d、IL1q、IL2d、IL2q、Isd、Isq、Icd、Icq、Vacd、Vacq分别为交流网侧Vp、Vc2、Vc3、Vc4、IL1、IL2、Is、Ic、Vac的dq轴分量。
根据图2的锁相环结构图,锁相环的状态方程如式(6)所示。
(6)

(7)
根据图1中的系统框图,可得直流回路系统的电路方程如式(8)所示。
(8)
式中:R0和L0分别为平抗的电阻和电感值;Cd1、Ld1、Cd2、Ld2、Cd3为直流线路的等效参数。式(3)、(5)、(6)和(8)中的f1至f25共25个方程即构成了高压直流系统的微分方程组,为便于分析,将上述方程组进行局部线性化得到系统相应的小信号模型,形成高压直流系统的状态方程如式(9)所示。

(9)
式中:ΔX为系统的状态变量矩阵的小信号值;ΔU为系统输入变量的小信号值;A为系统状态矩阵;B为系统输入矩阵。
根据上述数学模型,系统的状态变量矩阵为
(10)
系统状态矩阵A为f1到f25微分方程组对状态变量的偏导数矩阵,如式(11)所示。
(11)
系统输入矩阵B的表达式如式(12)所示。
(12)
为获得直流谐波阻抗,(9)式中输入变量U取为图1中直流端口外加小扰动谐波电压Vf。
根据欧姆定理,直流回路谐波阻抗表达式如式(13)所示。
(13)
式中:Vf0和Vf分别为加谐波电源前后的直流端口相应频率谐波电压;IDC0和IDC分别为加谐波电源前后的直流回路相应频率谐波电流。由于换流器数学模型中只包含基波分量,稳态时直流回路的谐波电压Vf0和电流IDC0均为0,则谐波阻抗Zf为谐波电压Vf与谐波电流IDC的比值,IDC根据式(9)进行拉普拉斯变换可得如式(14)所示。
(14)
式中(19)表示取矩阵第19个元素。则由式(13)和式(14)可得直流回路的谐波阻抗表达式如式(15)所示。

(15)
通过式(15)可得高压直流换流器直流谐波阻抗的s域状态空间表达式,将s域变换到频域,即可得到直流谐波阻抗的频谱。
3 仿真验证
为验证上述理论的有效性,本文在MATLAB中建立了图1中换流器系统的直流回路阻抗的计算程序,换流器系统的参数如表1所示。

表1 系统主要参数Tab.1 Main parameters of the system
根据MATLAB程序计算得到图1系统的直流回路阻抗频谱如图3所示。

图3 高压换流器直流回路阻抗频谱Fig.3 Impedance spectrum of DC loop of high voltage converter
可见该系统的直流回路阻抗在50 Hz左右有一个最低值,且阻抗随着频率升高而不断增加。
为验证图3结果的准确性,本文基于图1的系统框图和表1系统数据在PSCAD/EMTDC中搭建了仿真模型。为得到直流谐波阻抗,仿真时在换流器直流出口即图1中Vf处配置小干扰谐波电压源Vh,仿真开始时Vh的谐波幅值为零,当系统直流即IDC达到额定并保持稳定后,开始将Vh设置为不同的频率fp和幅值Vhp,此时IDC中会出现相应不同频率的谐波电流IDCp,则各频率点fp的直流回路阻抗为
(16)
式中:Vhp0和Vhp分别为加谐波电源前后的直流端口相应频率谐波电压;IDCp0和IDCp分别为加谐波电源前后的直流回路相应频率谐波电流。且Vhp0、Vhp、IDCp、和IDCp0均由FFT分析得到。则根据式16可以得直流回路各频率点的实际阻抗值,如图4中红点所示。

图4 直流回路谐波阻抗仿真值与计算值对比图Fig.4 Comparison of the simulated and calculated values of the DC loop harmonic impedance
由图4可见,PSCAD仿真所得的直流谐波阻抗与MATLAB计算所得阻抗曲线吻合较好,证明本文所提的基于状态方程的高压换流器直流回路谐波阻抗计算的方法准确可用。
4 谐振抑制方法
由式(15)可知,直流回路的谐波阻抗跟矩阵A和矩阵B相关,而矩阵A和B根据其表达式可知与高压换流器系统的一次设备参数和控制系统参数都相关,所以适当调整系统一次设备或控制系统参数均能改变直流回路谐波阻抗。而一次设备由于受到占地和成本等限制,调整不太灵活,本文主要研究通过调整控制系统参数来改变直流回路阻抗,从而在不改变系统占地和成本的情况下,实现对直流回路谐振的主动灵活抑制。
基于上述的系统模型和参数,保持其他参数不变,分别只改变某一个控制参数,可得直流回路阻抗频谱随各控制参数变化的关系如图5—9所示。
图5中曲线为Kp从0.6按1的步长增加到6.6时的波形,Kp由小增大时,曲线的颜色由红(深)变绿(浅)。可见,Kp改变时,直流回路阻抗的曲线发生了较明显的改变。其中,不同频带的阻抗随Kp变化的规律并不相同:80 Hz以内的阻抗曲线与Kp的值呈正相关的变化规律,Kp增加时,阻抗曲线上升,初始的阻抗最低点也逐渐消失,该频段内直流谐振风险逐渐降低;80~150 Hz之间的阻抗曲线随着Kp的增加而呈现减小的趋势,且Kp增大到一定程度时,该频段内甚至出现了新的谐振点,谐振风险增加;高频部分的阻抗曲线受Kp变化的影响不大,且该频段内的阻抗本身就较大,可以忽略Kp对高频段阻抗的影响。
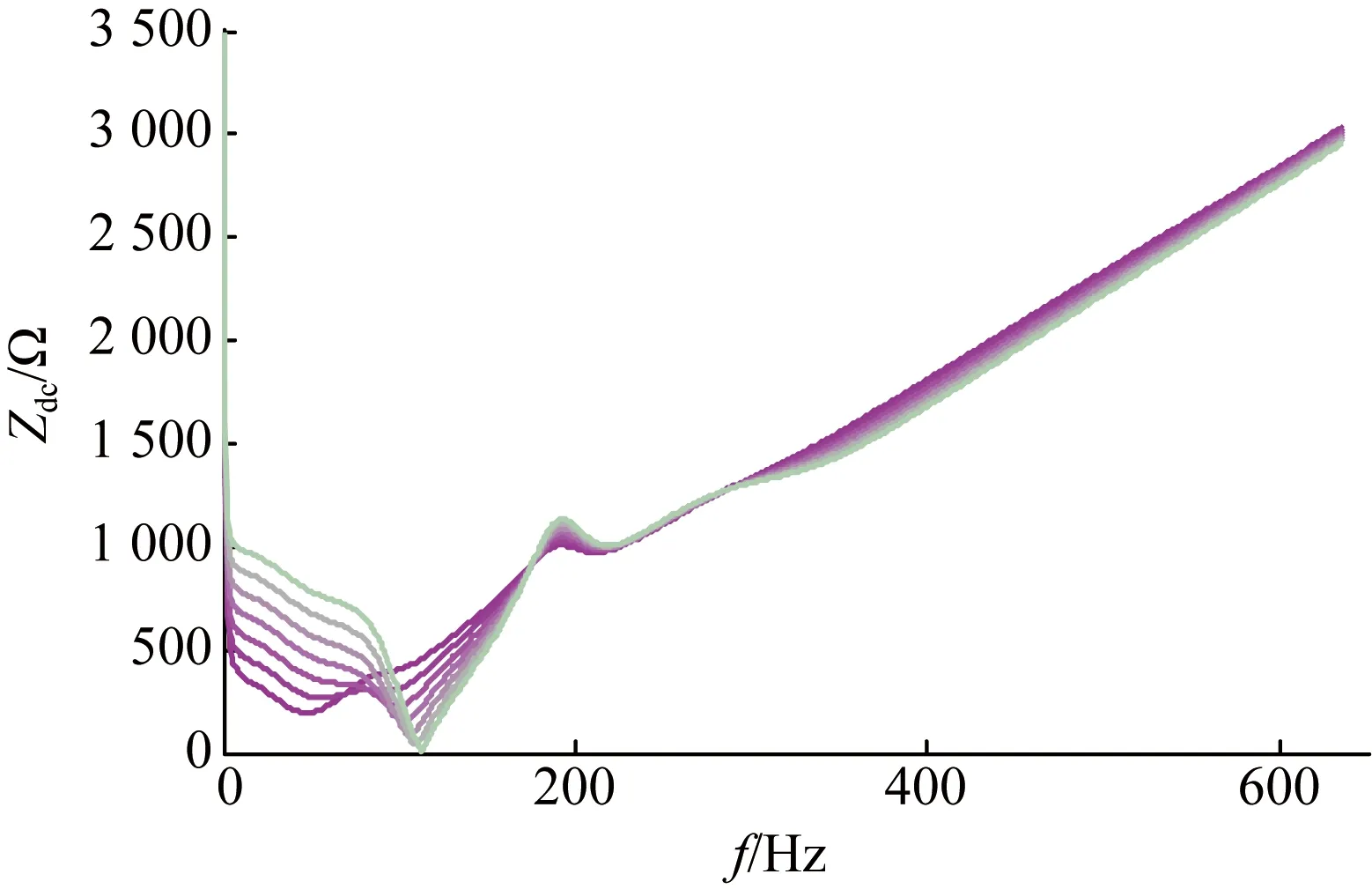
图5 Kp变化时的阻抗曲线Fig.5 Impedance curve when Kp changes
图6中曲线为Ki从41按150的步长增加到1 150时的波形,Ki从小增大时,曲线的颜色由红(深)变绿(浅)。可见,Ki改变时,直流回路阻抗的曲线发生了较明显的改变。同样,不同频带的阻抗随Ki变化的规律并不相同:50 Hz以内的阻抗曲线与Ki的变化呈正相关;50~100 Hz频段的阻抗与Ki的变化呈负相关,且Ki增加到一定程度时,该频段出现了新的谐振点;高频部分的阻抗曲线与Ki变化相关性较小,可以忽略。
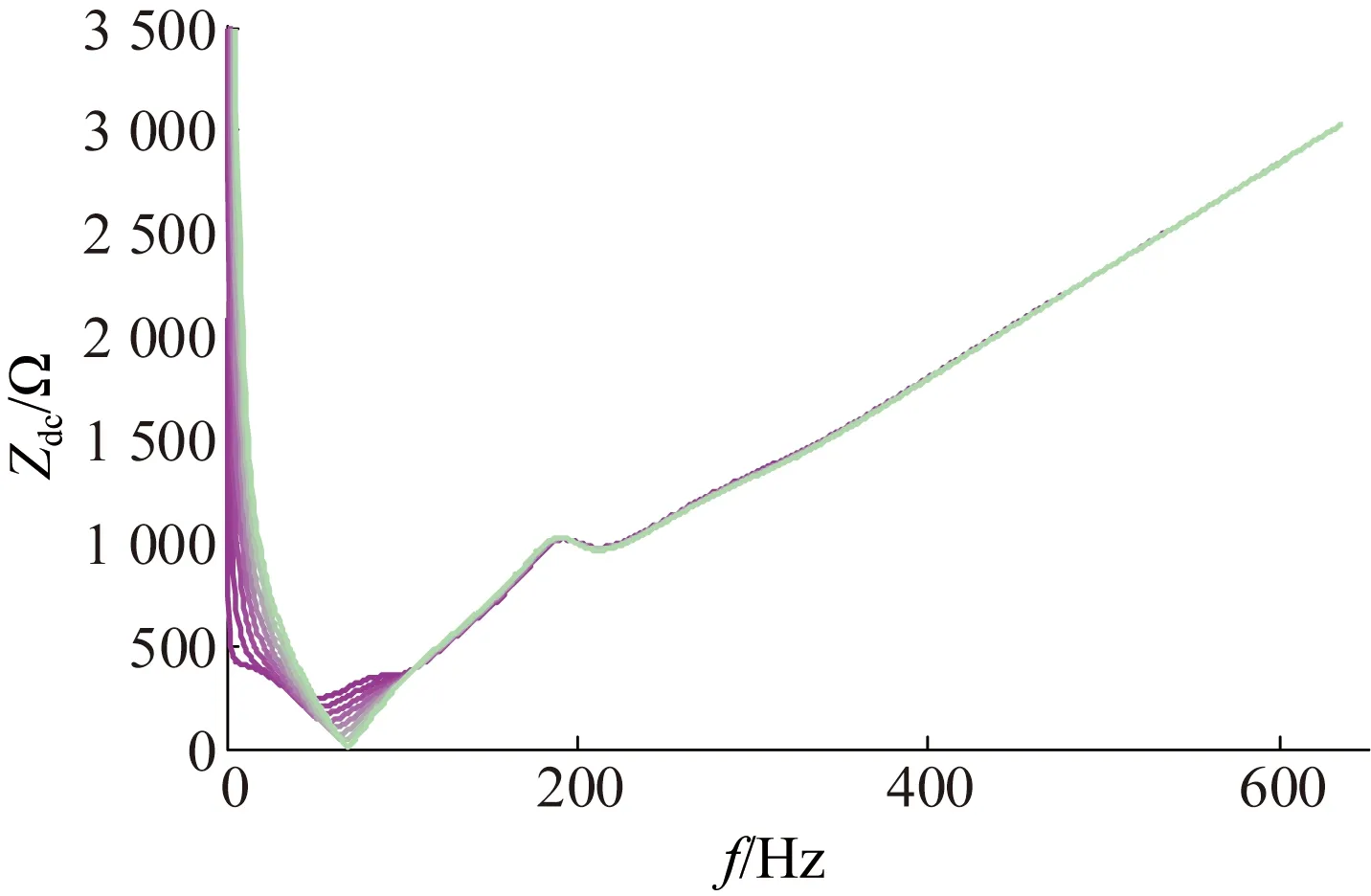
图6 Ki变化时的阻抗曲线Fig.6 Impedance curve when Ki changes
图7和图8中分别为KpPLL和KiPLL变化时的阻抗曲线,KpPLL和KiPLL参数变化时,直流谐波阻抗曲线几乎没有改变,可见直流回路谐波阻抗与锁相环的参数相关性不大。
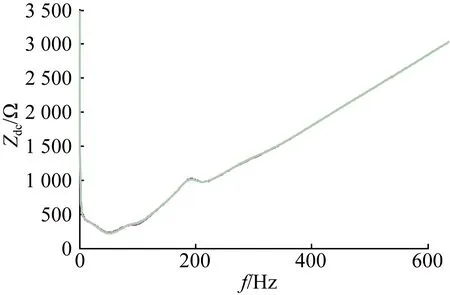
图7 KpPLL变化时的阻抗曲线Fig.7 Impedance curve when KpPLL changes

图8 KiPLL变化时的阻抗曲线Fig.8 Impedance curve when KiPLL changes
图9中曲线为T1从0.1 ms按1 ms的步长增加到5 ms时的波形,T1从小增大时,曲线的颜色由红(深)变绿(浅)。可见,T1增加时,50 Hz附近的阻抗曲线逐渐降低,100~200 Hz频段的阻抗逐渐增加,高频部分的阻抗曲线与T1变化相关性较小,可以忽略。
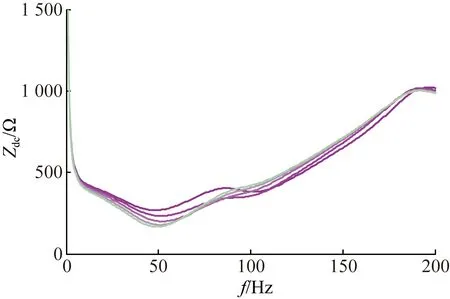
图9 T1变化时的阻抗曲线Fig.9 Impedance curve when T1 changes
各参数变化时直流阻抗曲线的变化规律如表2所示。
由以上分析可知,直流回路谐波阻抗与Kp、Ki和T1都紧密相关,当存在特定频率的干扰谐波电压时,根据表2的规律适当改变Kp、Ki和T1可以定向调整直流谐波阻抗,避免直流回路在特定频率产生谐振的风险。
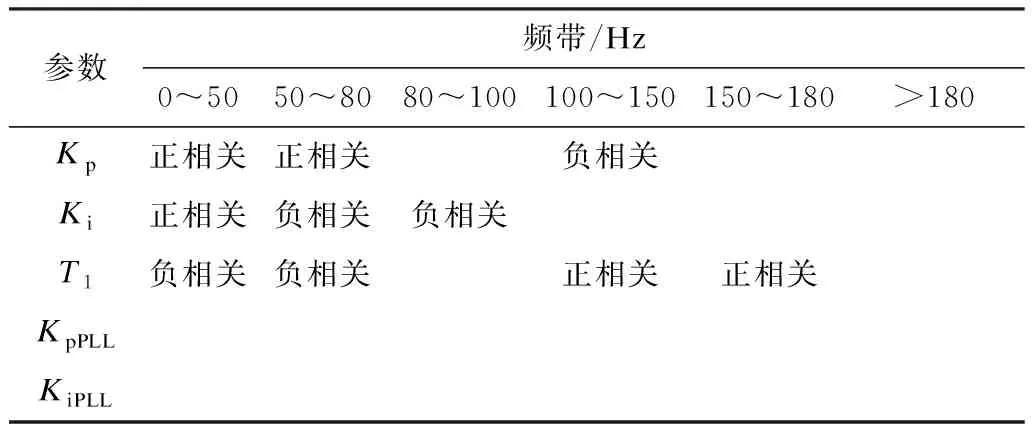
表2 各频带直流谐波阻抗值与各控制参数的相关性Tab.2 The correlation between the DC harmonic impedance value of each frequency band and each control parameter
下面以调整Kp为例来对上述方法进行仿真验证,图10中对比了Kp为0.6和2.6时的谐波电流波形,谐波电压Vf频率为50 Hz,幅值为1.9 kV,其中红色和绿色分别对应Kp为0.6和2.6时的电流波形,可见Kp增加时,谐波电流明显减小,与表2中特性一致。
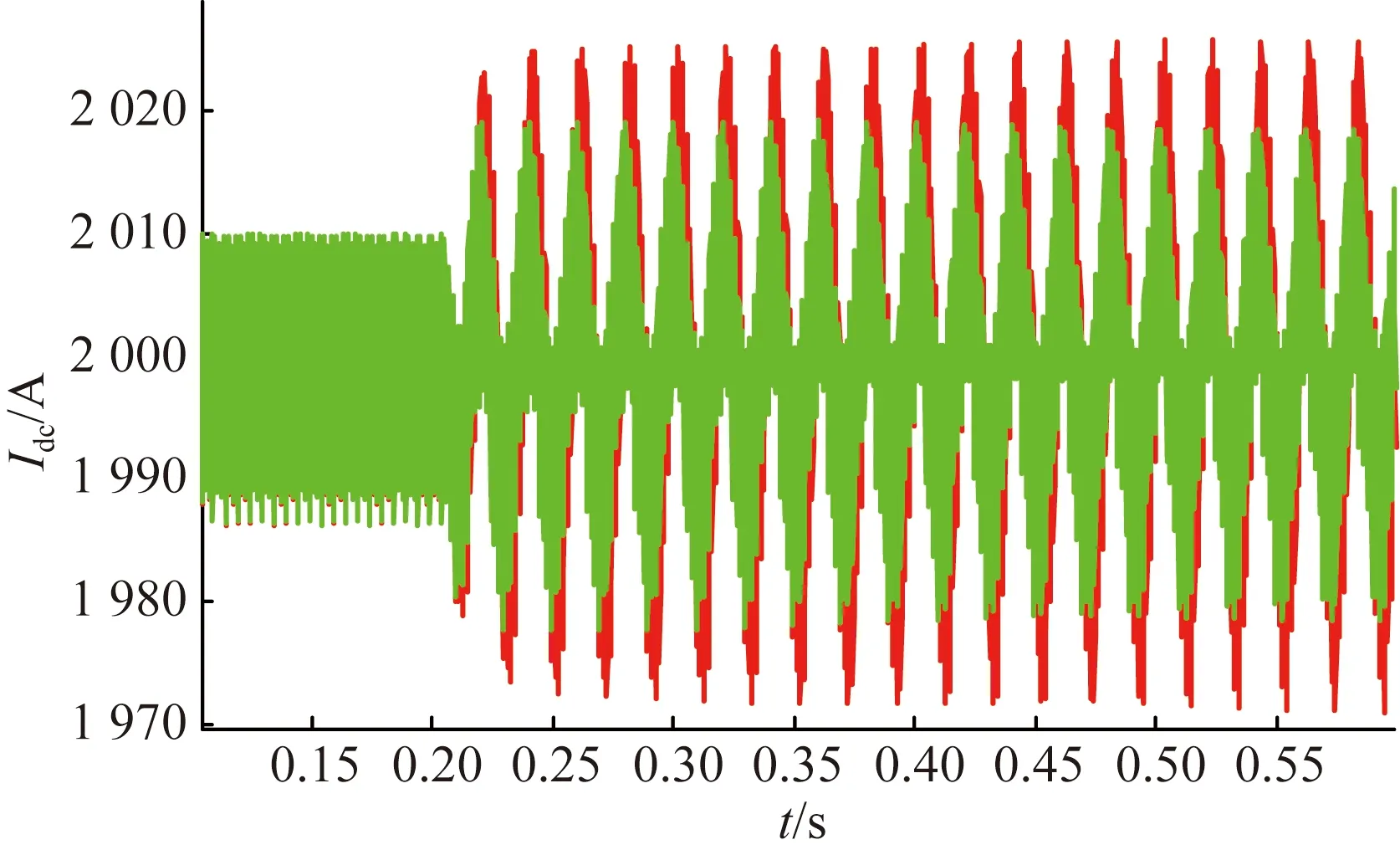
图10 Kp变化时的电流曲线Fig.10 DC current curve when Kp changes
上述基于控制参数调整的直流谐振抑制方法省去了阻波器等主设备,减少了设备种类、设备损耗、系统投资、占地和运维人员的工作量;提高了系统紧凑性和可靠性;当出现谐振问题时,通过适当改变控制器参数,就可实现对直流回路谐波阻抗的高效宽范围的主动调整,可以灵活便捷的应对直流回路发生的各个频次的谐振,无需对一次设备进行重新设计、拆装和测试,节约了时间成本和投资成本,直流谐振抑制能力得到显著提升。
5 结论
基于状态方程的方法,本文建立了高压直流换流器直流回路阻抗的数学模型,统一考虑了交流电网、交流滤波器、非线性换流器、直流线路和控制系统等各环节的动态特性,形成了高压直流换流器直流回路谐波阻抗的解析计算方法。
本文搭建了直流回路谐波阻抗的MATLAB计算程序,基于该程序通过解析计算,得到了高压直流换流系统的直流回路的阻抗频谱曲线,并采用PSCAD/EMTDC仿真软件得到了逐个关键频率点的直流回路阻抗,验证了本文所提模型算法的准确性。
本文分析了Kp、Ki、KpPLL、KiPLL和T1等控制系统参数变化时,直流谐波阻抗频谱的波动趋势,得到了影响直流谐波阻抗的关键参数,梳理了不同频段谐波阻抗随各关键参数的变化规律,形成了直流谐波阻抗定向调整和直流回路谐振的主动抑制方法。
本文所提的直流回路谐波阻抗的解析计算方法,提高了直流谐波阻抗的计算效率,形成了基于控制参数调制的直流谐振主动抑制方法,避免了额外一次谐振抑制设备的引入,降低了系统的设计、投资成本和占地,提升了高压直流换流器抑制直流谐振的灵活性和经济性,提高了系统的整体稳定运行水平和可靠性。

