一种小型弹用发动机空中起动环境模拟试验主动抗扰控制方法

王 信，钟华贵，2，但志宏，2，罗载奇，郭 强

(1.中国航发四川燃气涡轮研究院，四川绵阳 621000；2.高空模拟技术重点实验室，四川绵阳 621000)

1 引言

小型弹用发动机起动过程具有起动惯性小、起动时间极短(几秒)、流量变化率大、起动边界窄等显著特征，其起动过程对高空模拟试车台(简称高空台)进、排气环境压力压差变化极为敏感。一旦进、排气压力控制不稳定或偏差较大，将会导致起动试验失败。因此，高空台飞行环境模拟控制方法必须具有较强的抗干扰性和鲁棒性，才能较为准确地模拟发动机起动过程飞行工作环境的变化。

某小型弹用发动机空中起动环境模拟试验最初采用了常规PID控制，存在压力超调量大、收敛时间长、单组参数难以适应起动过程压力快速变化等问题。这是因为常规PID 控制在控制目标跳变时，存在被控对象易超调、微分信号易被噪声污染致使微分控制难以实现等缺陷[1]。为此，又设计了一种前馈+PID反馈的复合控制方法，根据发动机起动规律进行前馈补偿，能及时有效地抑制发动机起动对被控压力的干扰和动态影响。但此方法对被试发动机准确的起动特性或精确数学模型依赖性较高，控制参数需根据被控对象特性和工况改变重新调整。因此，急需寻找一种能适应不同模拟工况、通用性和快速性较好的强抗扰控制方法以提高模拟品质和试验成功率。

Sastry 设计了一种自适应控制方法，利用系统辨识生成控制系统模型，根据系统工况的动态变化自动更新控制参数。Luppold 开发了一种基于扰动前馈和PID反馈的控制方法，将风扇转速、发动机动态特性等生成增益调度表进行前馈控制[2]。上述控制方法均对被控对象精确数学模型依赖性较高，而高空台难以对每台被试发动机进行精确建模，因此其通用性较差，难以推广。

韩京清[3]于1998年首先提出了自抗扰控制技术(ADRC)，将被控对象转化为积分串联型系统构造理想控制器，将系统未建模动态信息和位置扰动作用当作对系统的扰动而自动估计并给与补偿。2003年，高志强[4]提出一种自抗扰控制器参数调节方法，将调参问题简化为控制器和观测器带宽调参问题，使自抗扰控制方法推广应用成为可能。孙亮等[5]在交流伺服系统中对其进行了仿真验证，袁东等[6]验证了该参数配置方法的可行性并在武器控制系统中应用。目前，自抗扰控制方法已在船舶动力定位控制[7]、导弹控制[8]、火电厂温度控制[9]等领域广泛应用。

本文基于自抗扰控制思想，提出一种用于高空台非线性不确定复杂系统的主动抗扰控制方法。通过对系统关键设备机理建模和设计主动抗扰控制器进行仿真研究，以期为弹用发动机空中起动试验新控制技术发展奠定理论基础。

2 飞行环境模拟系统模型

为避免新控制方法直接在高空台设备上调试带来的不确定风险，通过机理建模方式搭建仿真平台对主动抗扰控制方法进行仿真分析和验证。高空台结构如图1所示，按功能划分为PB、PC、PD和PM子系统。PB 子系统位于高空台进气管网与供气总管之间，主要用于保证供气机组背压使机组在安全的压比范围内工作，并为PC子系统提供稳定的进口压力；PC子系统位于PB子系统和发动机进口之间，主要对不同温度、压力的气体进行掺混调节(或直接调节)，模拟发动机高空飞行条件下的进气总压和总温实时变化；PD子系统位于发动机出口至排气调节阀X3 和X4 之间，主要通过对高空舱压力进行实时调节，保证飞行高度模拟的准确性。PM 子系统位于PD子系统和抽气机组之间，用于将发动机排出的低压燃气增压后排出至大气环境。

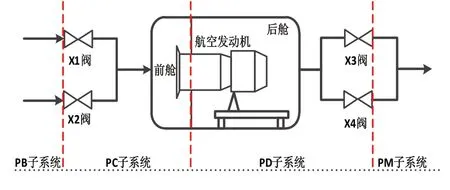
图1 高空台结构示意图Fig.1 Layout diagram of high altitude test facility

首先建立高空台关键设备模型，搭建仿真平台。仿真平台涉及的模型主要包括PC 子系统管网容腔模型、PD 子系统管网容腔模型、液压伺服执行机构模型和调节阀流量特性模型。

2.1 PC子系统管网容腔模型

PC子系统管网容腔主要由X1柱塞阀、X2蝶阀、试验舱前室结构、空气管道及流量管等组成。为简化分析，将其合理等效为一个容腔结构，如图2 所示。图中，X1 阀和X2 阀为进气调节阀，控制PC 子系统管网容腔压力；PC子系统管网容腔出口为发动机进口。

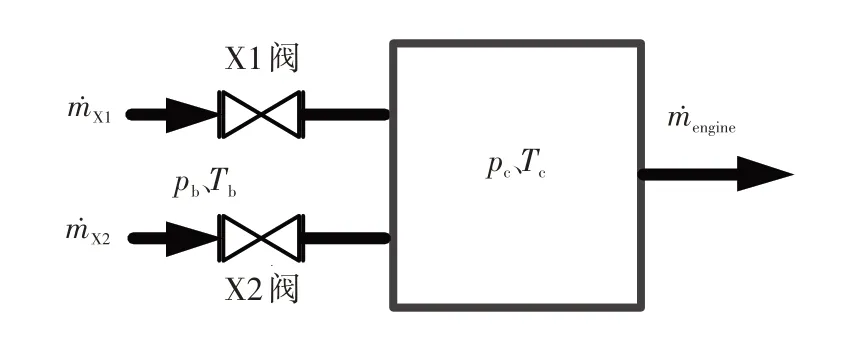
图2 PC子系统管网容腔结构简图Fig.2 Diagram of PC subsystem pipe network cavity

建立的PC 子系统管网容腔温度和压力的微分方程分别为：

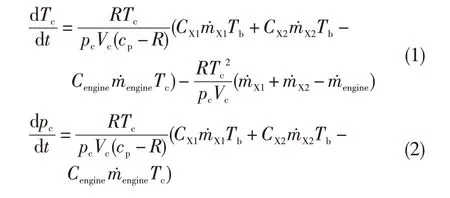
式中：Tc为PC 子系统管网容腔温度，pc为PC 子系统管网容腔压力，Vc为PC 子系统管网容腔容积，为X1 阀流量，为X2 阀流量为PC 子系统排气流量，cp为气体的比定压热容，R为气体常数，CX1为X1阀进气气流速度，CX2为X2阀进气气流速度，Cengine为PC 子系统管网容腔排气气流速度，Tb为PB 子系统出口气流温度。

2.2 PD子系统管网容腔模型

PD 子系统管网容腔主要由发动机出口、X3 蝶阀、X4 蝶阀、试验舱及空气管道等组成。为简化分析，将其合理等效为一个容腔结构，如图3所示。图中，X3 阀和X4 阀为排气调节阀，PD 子系统管网容腔进口为发动机出口，其压力由X3阀和X4阀控制。

图3 PD子系统管网容腔结构简图Fig.3 Diagram of PD subsystem pipe network

建立的PD 子系统管网容腔温度和压力的微分方程分别为：

式中：Tengine为发动机排气温度，pd为PD 子系统管网容腔压力，Vd为PD子系统管网容腔容积为X3阀流量，为X4阀流量，CX3为X3阀排气气流速度，CX4为X4阀排气气流速度。

2.3 液压伺服执行机构模型

液压伺服系统执行机构主要由电液伺服阀、液压缸、位移传感器等组成，液压伺服系统采用的控制器为比例控制器。建立的液压执行机构模型为：

式中：G1为电液伺服阀电信号到电液伺服阀流量的传递函数，G2为电液伺服阀流量到液压缸活塞位移的传递函数，KP为比例系数，KI为积分系数，Kq为流量增益，s为微分算子，ωsv为电液伺服阀的固有频率，ξsv为电液伺服阀的阻尼比，A为液压缸截面积。

2.4 调节阀流量特性模型

PC子系统和PD子系统均使用液压驱动的一大一小两台调节阀对进气压力或排气压力进行组合调节。调节阀流量特性模型采用文献[10]提出的流量计算方法建模，其质量流量计算公式为：

式中：φ为调节阀的流量系数，表征调节阀的流量特性；S为调节阀的流通截面积；T1、p1分别为调节阀前气流的温度和压力。由于T1、p1在试验中测得，S可以通过阀门开度计算得出，所以只需知道φ即可获得通过阀门的流量。

3 主动抗扰控制器设计

3.1 二阶系统状态空间

高空台飞行环境模拟系统的PC子系统和PD子系统模型均由液压伺服执行机构(伺服阀和液压缸等)、阀门、系统压力变化模型等组成。为简化研究，可将液压伺服执行机构简化为一阶惯性环节，将系统压力变化模型简化为积分环节，简化方法详见文献[11]。经过合理简化，PC子系统和PD子系统均可转化为典型的二阶系统。

建立二阶系统状态空间。以PC子系统为例：

将其写成：

式中：y、u分别为控制系统的输出和输入信号，w为外部扰动，f(y,,w,t)为系统总扰动。

该二阶系统状态空间为：

3.2 主动抗扰控制器原理

针对小型发动机起动试验设计的主动抗扰控制器的原理如图4所示。主动抗扰控制器主要由跟踪微分器、PD 控制器、扩张状态观测器等组成。跟踪微分器是小型发动机空中起动试验主动抗扰控制器的重要部分，主要用来获取光滑的输入信号，并安排过渡过程，解决响应速度与超调之间的矛盾，提高系统的稳定性。扩张状态观测器为自抗扰控制器的核心部分，将系统内部扰动和外部扰动及建模不确定性扩张为新的状态变量，实时观测该状态变量并实时补偿，将系统转化为一个积分串联型系统，提升控制系统的鲁棒性。PD 控制器为主动抗扰控制器的内核。

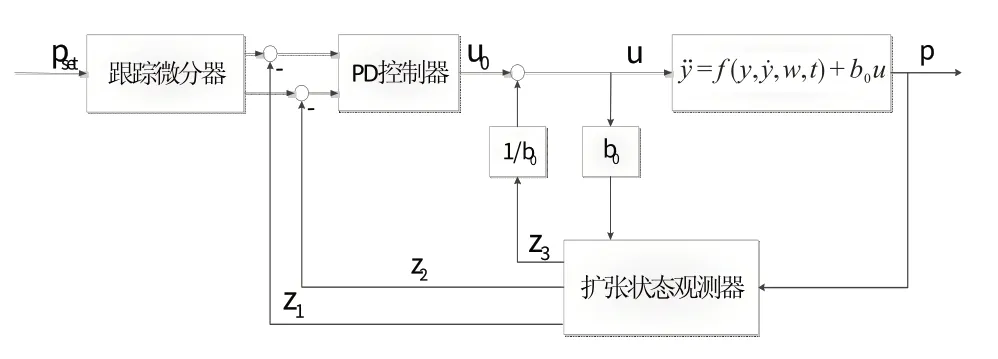
图4 主动抗扰控制器原理框图Fig.4 Principle block diagram of active disturbance rejection controller

3.3 扩张状态观测器设计

针对高空台飞行环境模拟系统被控对象，设计扩张状态观测器，如公式(12)所示：

式中：z1跟踪x1(被控量)，z2跟踪x2(被控量的微分)，z3跟踪x3(被控对象的总扰动，包括内扰和外扰)。

用(y-z1)代替非线性函数newfal(e,α,δ,γ)分析，可得式(12)的线性化方程：

设系统带宽为ω0，将扩张状态观测器特征方程的3个极点都配置在-ω0处，可简化扩张状态观测器的参数调整过程。β01、β02、β03可写成与ω0的关系，即β01=3ω0，β02=3ω02，β03=ω03。则观测器特征方程可化为：

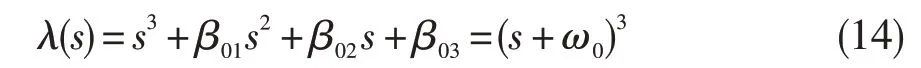
扩张状态观测器包括非线性和线性两种。由于高空台飞行环境模拟系统是由调节阀、液压缸、管网容腔等组成的一个非线性系统，为了对其内部扰动和外部扰动及建模不确定性等进行较为准确的观测，故需进行非线性扩张状态观测器设计。在设计非线性扩张观测器时，最早选用了非线性函数fal(e,α,β)：

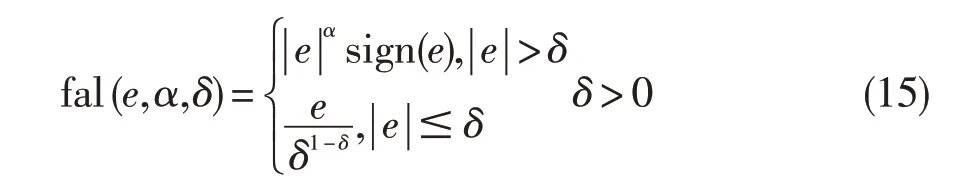
fal(e,α,β)的响应曲线虽然连续，但在线性区间δ较小时会产生高频颤振，导致系统性能较差。为此，采用刘丙友[12]提到的改造方法进行改进：

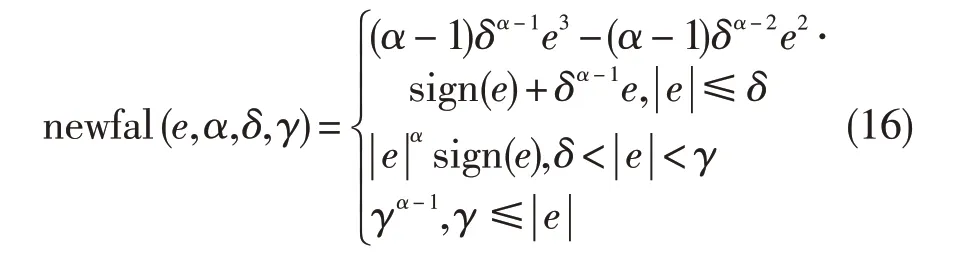
从上式看出，在e足够小的邻域内，newfal(e,α,δ,γ)近似为奇函数；当|e|足够大时，newfal(e,α,δ,γ)的值近似饱和，α=1.0 时newfal(e,α,δ,γ)的值是e；当γ≤|e|时，newfal(e,α,δ,γ)变为线性函数。图5 给出了newfal(e,α,δ,γ)的响应曲线。

图5 newfal(e,α,δ,γ)的响应曲线Fig.5 Response curve of newfal(e,α,δ,γ)

为对比分析fal(e,α,β)和newfal(e,α,δ,γ)的性能(尤其是原点附近)，设置α=0.03、δ=0.05，仿真结果见图6。可见，相比于fal(e,α,β)，newfal(e,α,δ,γ)在原点附近更光滑，线性度更好，依此设计的自抗扰控制器具有更快的响应速度和更小的超调量。故本文在设计主动抗扰控制器时，采用newfal(e,α,δ,γ)对扩张状态观测器进行改进。

图6 fal(e,α,β)和newfal(e,α,δ,γ)仿真结果对比Fig.6 Simulation results comparison of fal(e,α,β)and newfal(e,α,δ,γ)

3.4 PD控制器

设计控制律为：

针对改造后的积分串联系统，设计合适的PD控制器：

式中：r是设定值，KP为比例系数，KD为微分系数。

为简化参数整定过程，将积分串联系统的极点配置在-ωc处，即

式中：KP=ωc2，KD=2ωc。

与进气系统相似，排气系统可采用相同原理进行主动抗扰控制器设计。

4 仿真验证

针对小型发动机起动环境模拟试验，设计的主动抗扰控制器主要解决该发动机起动过程中进气、排气压力难于精确控制的问题。分别采用常规PID控制器和主动抗扰控制器进行主动抗扰测试仿真试验：仿真初始时刻(即发动机起动前)，PC子系统压力和PD 子系统压力均为a kPa(为某高度对应大气压力)；14 s时，PC子系统压力迅速升高2.0 kPa，建立发动机空中起动条件，发动机开始点火起动至慢车状态。

图7示出了采用常规PID控制的进、排气压力控制效果。可见，发动机起动过程中，PC 子系统压力最大偏差≯0.60 kPa，PD 子系统压力最大偏差≯0.30 kPa；PC子系统压力9 s恢复至稳定状态，PD子系统压力约20 s恢复至稳定状态，收敛时间较长，动态跟踪能力差。图8给出了主动抗扰控制器下的进、排气压力控制效果。可见，发动机起动过程中，PC子系统压力在动态调整过程中最大偏差≯0.30 kPa，进入稳态时间较短且无超调；PD子系统压力最大偏差≯0.15 kPa，进入稳态时间短。据此表明：基于ADRC的主动抗扰控制器能大幅改善控制系统的动态跟踪能力和稳态控制效果，收敛时间短，控制效果优于常规PID控制方法。

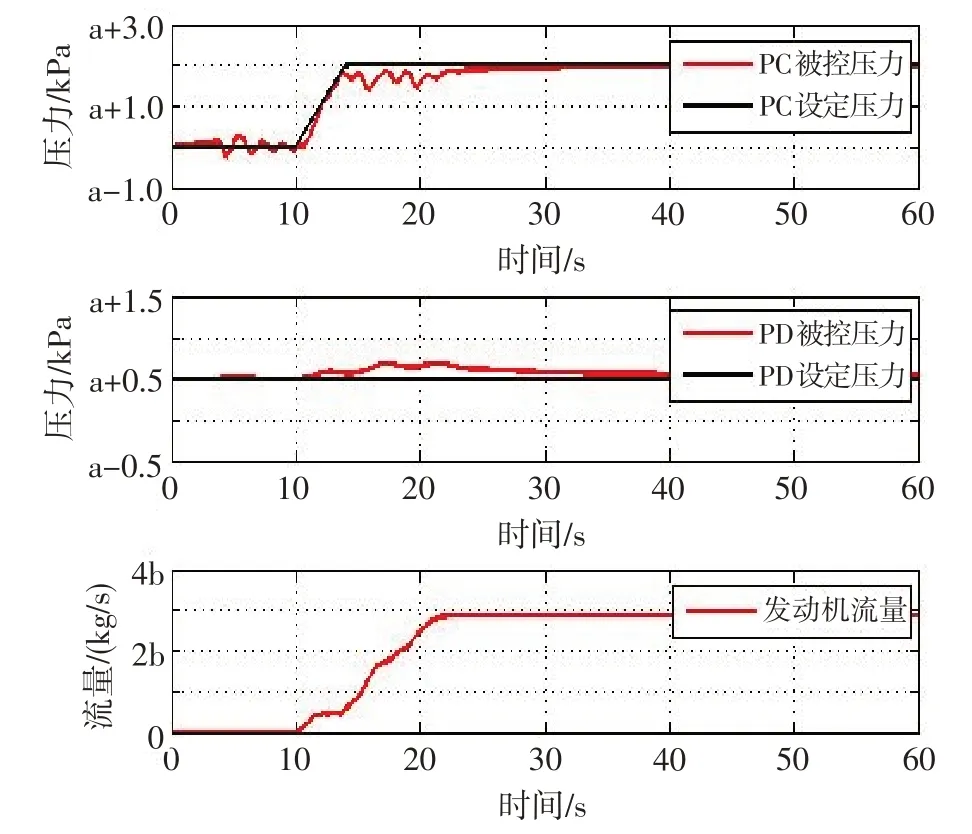
图7 常规PID控制仿真效果Fig.7 Simulation results of conventional PID control

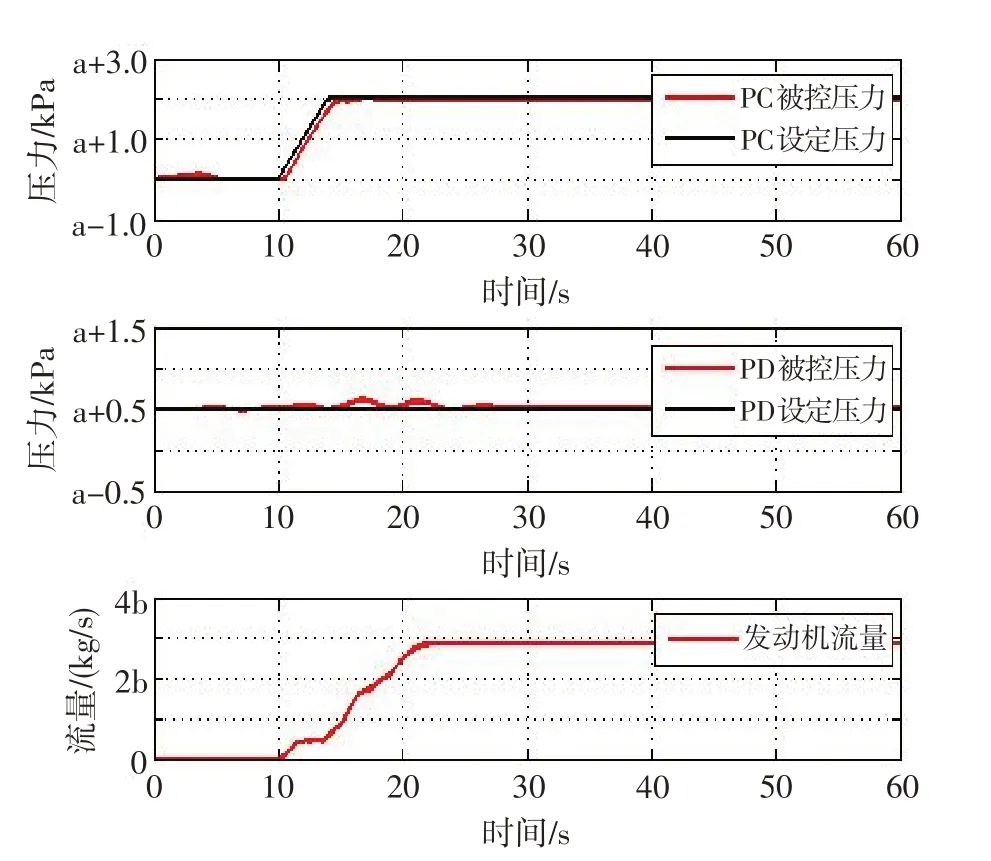
图8 主动抗扰控制仿真效果Fig.8 Simulation results of active disturbance rejection

5 结论

提出的基于自抗扰控制思想的主动抗扰控制方法，在弹用发动机空中起动环境模拟试验中实现了进、排气环境压力模拟的快速响应和精确控制，且进、排气控制偏差满足技术指标要求，控制效果优于常规PID 控制，是一种适合高空台非线性不确定复杂系统的控制方法，具有重要的工程应用价值。