材料性能分散性对轮盘破裂转速预测结果的影响研究

苏俊卿，李林骏

(中国航发四川燃气涡轮研究院，四川绵阳 621000)

1 引言

轮盘是航空发动机的断裂关键件，一旦破裂，会导致灾难性后果[1]。为保证航空发动机的安全性，国内外航空发动机规范和适航标准均对轮盘的强度设计提出了严格的要求，明确规定了轮盘的破裂转速储备设计要求[2-3]。如美国发动机结构完整性大纲军用标准[2]规定，轮盘的最低破裂转速不得低于最大允许稳态转速的122%。

根据规范要求，航空发动机结构设计时需要对轮盘构型进行设计优化，以保证其具有足够的破裂转速储备。国内外学者提出和发展了多种轮盘破裂转速预测方法[4-15]，如平均应力法、局部应变法、小变形解析法、大变形解析法等。在众多方法中，基于残余变形或塑性失稳准则的大变形有限元分析方法，主要利用轮盘材料的弹塑性本构模型来预测破裂转速，不需要通过实际轮盘破裂试验来修正方法本身，方便用于方案阶段的轮盘设计和优化。然而轮盘材料性能具有分散性，使用该方法进行破裂转速预测时，有必要了解和掌握材料性能分散性对其结果的影响规律。

本文针对GH4169轮盘，根据其拉伸性能数据，采用基于塑性失稳准则和大变形有限元分析方法，分别通过双线性、多线性和非线性三种轮盘材料本构模型来描述轮盘材料变形行为，分析材料性能分散性对轮盘破裂转速计算结果的影响。

2 基于双线性本构模型的轮盘破裂转速分析

利用双线性本构模型描述GH4169合金材料的弹塑性行为，通过大变形有限元分析方法计算GH4169 轮盘的破裂转速。考虑到所模拟轮盘材料性能及工作载荷的对称性，仅建立整体轮盘的1/12扇形有限元模型(图1)，设定循环对称边界条件，实现对整体轮盘的计算分析。

图1 轮盘模型Fig.1 Model of disc

双线性本构模型采用两段线性方程来描述材料的响应曲线，对真应力-真应变曲线拟合度低，计算量小。表达式如下：

式中：σ为应力，E为弹性模量，ε为应变，σy0为初始屈服应力，εy0为初始屈服应力下的应变，E1为切线模量。对于双线性本构模型，弹性模量、泊松比、屈服应力、切线模量是决定材料性能的主要参数。

通过试验测得GH4169 合金试样的弹性模量、泊松比、屈服应力、切线模量，将平均值作为基准值，设定系数k为基准值的倍数，以表示各性能参数分散性的取值范围。在研究其中某一性能参数的分散性对破裂转速计算结果的影响时，均假设其他参数取基准值。表1～表4 分别给出了弹性模量、泊松比、屈服应力、切线模量在典型分散范围内基准值上下变化时，轮盘破裂转速预测结果及其与取基准值时预测结果的偏差。

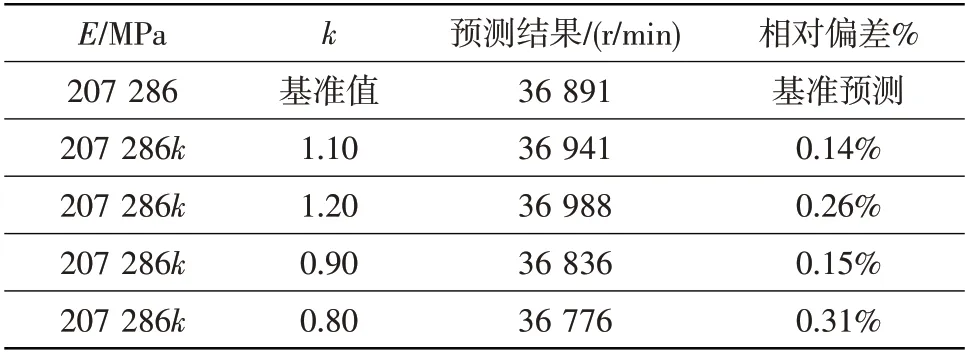
表1 弹性模量分散性对轮盘破裂转速预测结果的影响Table 1 Contrast of prediction results of disc burst speed under different elastic modulus

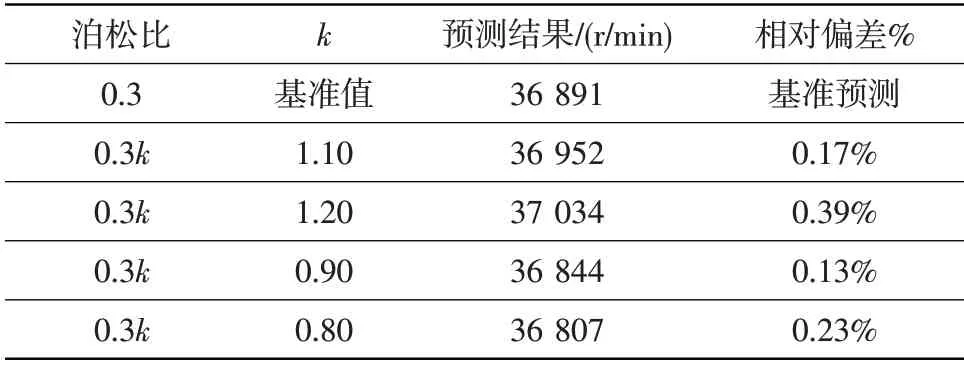
表2 泊松比分散性对轮盘破裂转速预测结果的影响Table 2 Contrast of prediction results of disc burst speed under different Poisson ratio

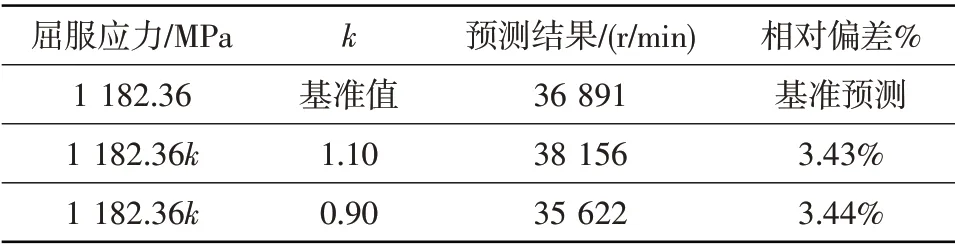
表3 屈服应力分散性对轮盘破裂转速预测结果的影响Table 3 Contrast of prediction results of disc burst speed under different yield stress

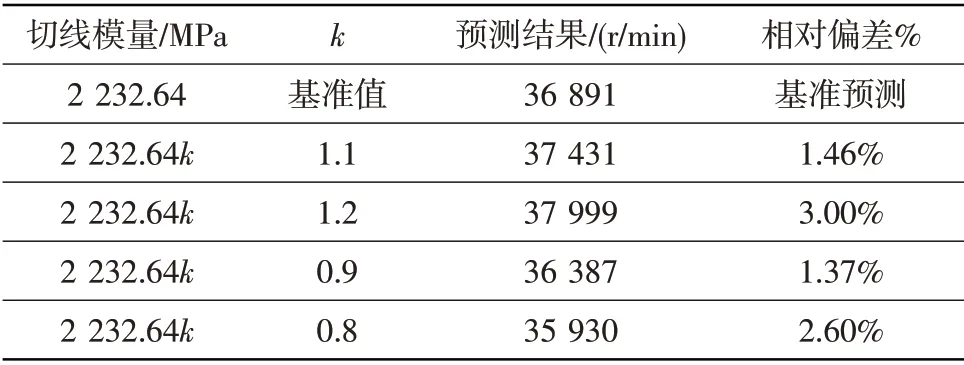
表4 切线模量分散性对轮盘破裂转速预测结果的影响Table 4 Contrast of prediction results of disc burst speed under different tangent modulus

从表1和表2对比结果可以看出，弹性模量和泊松比在基准值上下20%范围内变化时，破裂转速预测结果偏差小于0.50%，影响较小。从表3和表4结果可以看出，屈服应力和切向模量分散性对破裂转速预测结果的影响相对较大。屈服应力在基准值上下10%范围内变化时，破裂转速预测结果偏差在4.00%以内。切线模量在基准值上下20%范围内变化时，破裂转速预测结果偏差在3.00%以内。因此，当轮盘材料性能参数在典型分散范围内变化时，基于双线性本构模型预测的轮盘破裂转速偏差较小，材料性能分散性对预测结果的影响较小。

3 基于多线性本构模型的轮盘破裂转速分析

轮盘有限元计算模型同图1。多线性本构模型是将试验测得的材料真应力-真应变曲线采用多条直线段来描述，对真应力-真应变曲线拟合度较高，计算量适中。多线性本构模型表达式如下：

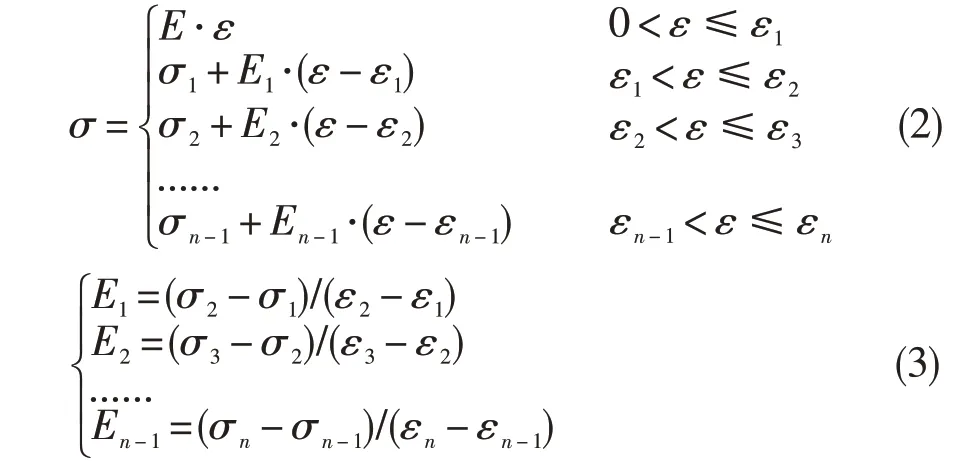
式中：(σ1,ε1)、(σ2,ε2)……(σn,εn)为多线性材料模型各分段的端点，E1、E2……En-1为各分段斜率。

试验测试获得10 条典型GH4169 光滑圆棒试样拉伸真应力-真应变曲线，其拉伸性能分布在典型分散范围内。采用10 个多线性本构模型来描述，拉伸强度从小到大依次排列，分别为多线性1至多线性10，最大拉伸强度与最小拉伸强度相差约100 MPa，如图2 所示。基于10 种多线性本构模型预测轮盘破裂转速，选择拉伸强度最低的多线性本构模型1 的预测结果作为基准，其他本构模型的预测结果与其对照，见表5。

图2 各多线性本构模型真应力-真应变曲线Fig.2 True stress-true strain curves of various multi linear models

综合图2和表5可看出，拉伸强度越大轮盘破裂转速预测值越大；不同拉伸强度下材料真应力-真应变拟合曲线不同，存在分散性，由材料分散性影响的破裂转速的预测结果相对偏差在3.00%以内。据此，当轮盘材料拉伸性能曲线在典型分散范围内变化时，基于多线性本构模型预测的轮盘破裂转速偏差较小，材料性能分散性对预测结果影响较小。

表5 各多线性本构模型的轮盘破裂转速预测结果及对照Table 5 Prediction results of disc burst speed based on various multi linear models

4 基于非线性本构模型的轮盘破裂转速分析

轮盘有限元计算模型同图1。非线性本构模型对材料的真应力-真应变曲线的拟合度最高，但计算量大。典型的非线性本构模型是采用公式(4)来描述材料拉伸真应力-真应变曲线的塑性变形。

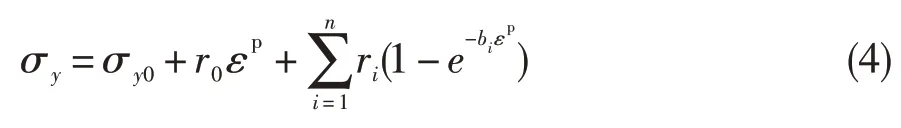
式中：σy为材料塑性流动应力；εp为塑性应变；r0、ri、bi为非线性本构模型参数；为能够较好地描述材料塑性变形曲线同时考虑计算量，本文n取4。

基于前述10条典型的GH4169光滑圆棒试样拉伸真应力-真应变曲线，采用非线性本构模型来描述，拉伸强度从小到大依次排列，分别为非线性1至非线性10(图3)。基于10种非线性本构模型预测的轮盘破裂转速见表6，仍选择拉伸强度最低的非线性本构模型1的预测结果作为基准。

图3 各非线性材料模型真应力-真应变曲线Fig.3 True stress-true strain curves of various non-linear models

从表6 中可看出，与多线性本构模型预测结果相似，拉伸强度越大，采用非线性本构模型预测的轮盘破裂转速也越大。相对于拉伸强度最小的非线性本构模型1 的预测结果，相对偏差均在3.00%以内。据此，当轮盘材料拉伸性能曲线在典型分散范围内变化时，基于非线性本构模型预测的轮盘破裂转速偏差较小，材料性能分散性对预测结果影响较小。

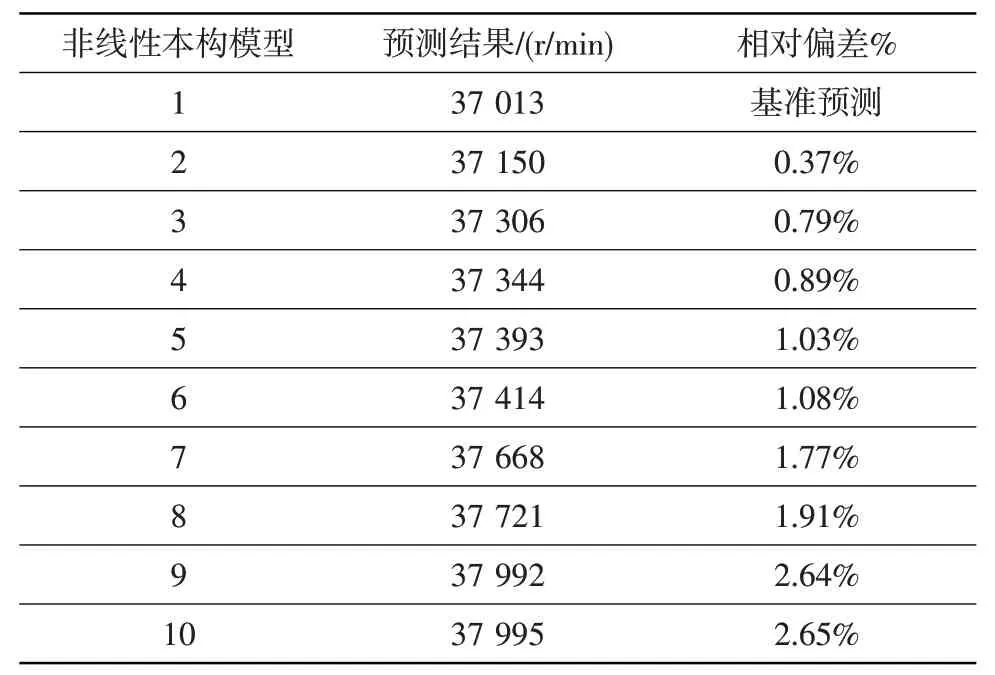
表6 各非线性本构模型的轮盘破裂转速预测结果及对照Table 6 Prediction results of disc burst speed based on various non-linear models

5 结论

针对GH4169 轮盘，采用基于塑性失稳准则和大变形有限元分析方法，分别利用双线性、多线性和非线性本构模型，计算分析了材料性能分散性对轮盘破裂转速预测结果的影响。结果表明，在典型分散范围内，材料性能分散性对轮盘破裂转速预测结果有一定影响，但影响较小。采用基于塑性失稳准则和大变形有限元分析方法预测轮盘破裂转速，可不考虑材料性能分散性造成的影响，直接采用材料最差性能真应力-真应变曲线进行预测，以获得相对保守更为安全的结果。