从认知心理学的角度谈数学思维分类问题

罗敏娜

【摘要】数学教学主要是思维教学，在数学中思考问题和解决问题都离不开数学思维.数学思维的分类并不是孤立的，每种思维都是互相联系、相互作用的，不同特点的思维在数学中起着不同的作用.

【关键词】认知心理学;数学思维;基本类型

思维作为一种人类大脑的基本活动方式，是一种对客观现实的概括和反映.由于各种数学活动的目的不同，因此有关数学的思维方式也不同.本文将从思维的方式、广度、灵活性、复杂性、结果等五个角度对数学思维进行分析.

一、逻辑思维和直觉思维

从思维的方式来分，思维可分为逻辑思维和直觉思维.

（一）逻辑思维

逻辑思维是以思维方式为依据划分的一类思维.逻辑思维在数学教学中是非常重要的一种思维活动，主要特点是以数学的基本概念、基本理论、基本公式为依据，利用分析法、综合法、概括法、归纳法等多种方法进行抽象和演绎，用数学符号得出结论.

例1 一个棱长为8厘米的正方体木块，表面全部涂上颜料，然后把它分成棱长是2厘米的小正方体若干块，其中三面涂有颜料、两面涂有颜料、一面涂有颜料、没涂颜料的各有多少块？

分析 首先启发学生说出正方体的特点，最好动手画出图形，然后探讨把大正方体分成棱长为2厘米的小正方体怎样分割，最后观察图形得出结论.

解 有8块三面涂有颜料，有24块两面涂有颜料，有24块一面涂有颜料，有8块没有涂颜料[1].

（二）直觉思维

直觉思维是指通过观察能够快速领悟到对象的性质和特点的一种思维活动，主要是以思维的直观性为特征.直觉思维不要求有一定的依据，这样就可以使学生跳过逻辑论证的环节，立即做出猜想，即是突然認知的，在一刹那时间内完成的.

（三）逻辑思维与直觉思维的关系

逻辑思维是对在大量的直觉思维的基础上提出的大胆猜想的严格论证.直觉思维必须以逻辑思维的方法为基础，逻辑思维方法作为组成因素渗透在直觉思维的过程中，是更高级的思维形式和方法.

二、孤立思维和网络思维

从思维的广度来分，思维分为孤立思维和网络思维.

（一）孤立思维

孤立思维是指在某种单一情境中进行的思维活动，主要特点是思维的目标方向确定，相互关联的知识点比较单一，思考问题的过程比较简单.例如，立体几何中垂线定理这一节课的例题和习题，都只能联想到垂线定理及其逆定理，学生只能从这两个方面思考.

（二）网络思维

网络思维是在实际环境中进行的思维，它的特点主要表现为能够根据题目迅速联想，并择优试用.学生在数学学习中获得的知识越来越多，纵向与横向形成知识网络，扩充了知识结构，并在大脑记忆系统中构建了数学认知结构，形成了一个条理化、有序化、网络化的有机体系，从而优化解题过程[2].

（三）孤立思维和网络思维的关系

网络思维是根据题目的条件能够迅速产生很多想法，通过思考择优选出最适合的一种方法的思维过程.而孤立思维只是根据当节讲的内容和例题，在做题过程中产生同样的解题思路，方法单一，纵向与横向之间没有形成知识网络.

三、惯性思维和求异思维

从思维的灵活性来分，思维分为惯性思维和求异思维.

（一）惯性思维

惯性思维是根据思考的常规模式或者人的思考习惯进行的思维活动，它的主要特点是与人的常规下思维方式相一致，思考过程中可以促使我们去联想，但思考过程缺乏一定的创新性和多样性.例如，求最值问题时，我们常常建立一个二次函数去解答.再如，在题目中出现 “至多”“至少”“不大于”等词语时，我们经常想到要用反证法去证明，这些都是一种惯性思维方式的体现.

例3 求证：四边形至少有一个内角的度数小于或等于90°.

分析 对于这样的问题，我们采用反证法去思考，通过推理得出与已知矛盾，即可证明假设是错误的，所以四边形至少有一个内角的度数小于或等于90°.

（二）求异思维

求异思维是违反常规的思维，如反向思维、对立思维、悖向思维等，它的特点是与平时的思维习惯相反.

在数学解题过程中，我们经常会想到的是几何题用几何方法来做，代数题用代数方法解决，这是一种单一思维方式，也是思维的常规性体现.而这里说的求异思维是指几何题用代数方法解决，代数题用几何方法解决.

（三）惯性思维与求异思维的关系

求异思维向惯性思维的转换就是建立新的思维定式，惯性思维的打破就是求异思维，对求异思维概括和总结的结果可以进一步丰富惯性思维.学生在学习数学的过程中，对求异思维的训练是思维定式的一个重大突破，学生在学习新知识时，要建立新的更高层次的思维模式，求异思维便是很好的体现.

四、单一思维和综合思维

从思维的复杂性来分，思维分为单一思维和综合思维.

（一）单一思维

单一思维是在思考问题时运用一种思维方式进行思考的思维活动，它的主要特点是思维的难度很低，思维格式单一，思维比较清楚.例如，利用数学归纳法证明题时，它的思维格式比较清楚，只要记住并直接套用即可，不容易造成错误.

（二）综合思维

综合思维是指同时运用多种思维方式进行思考的过程，它的主要特点是多种思维方法有机结合，多种思维之间的关系是相互补充.

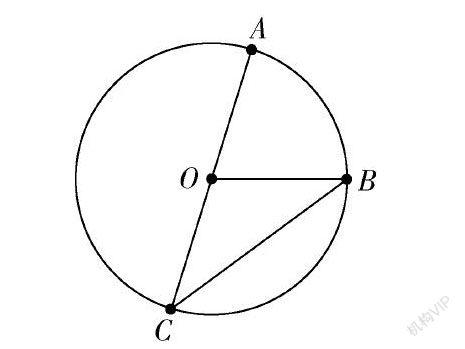
例6 求证：同弧所对的圆周角等于它所对的圆心角的一半.

证明 如图所示，画一圆，圆心为O，在圆上取两点A，B，连接AO并延长交圆O于C点，连接CB，OB，∠ACB为劣弧AB所对的圆周角，∠AOB为劣弧AB所对的圆心角.

显然∠AOB=∠ACB+∠CBO.

因为OC与OB为圆O的半径，所以OC=OB，