自助金融设备圆弧通道驱动轮组对钞票运行的影响

李 智，张 泉

（1.天津大学机械工程学院，天津300350；2.恒银金融科技股份有限公司博士后科研工作站，天津300308）

1 引言

自动取款机（Automatic Teller Machine，ATM）和存取款一体机（Cash Recycling Machine，CRM）是常见的自助金融设备，是集电子、机械于一体的自动化装置，主要用于现金的存取业务，只需少量的人工干预即可完成日常的现金流转业务。现金在设备中运行是由主动轮和被动轮组成的轮组驱动，轮组将钞票夹持在通道的中间。为节省空间，自助金融设备内部通道会出现多次弯曲与回转，因此钞票在通道中需要弯曲反转。反转过程中钞票沿着圆弧通道外圈移动，到达下一组驱动轮时，会发生钞票前端碰撞轮组的情况。实践过程中发现，如设计结构不合理，撞击力会损坏钞票前端，并造成拥堵的问题。钞票前端因与轮组碰撞而出现弯折，实验过程中钞票以宽度方向为前进，钞票长边为运动过程的前端。因此对圆弧通道和轮组排布进行研究，分析其对钞票的影响，如图1所示。2005年韩国学者Ryu研究了纸张传输过程中辊轮压力和传输速度对纸张滑移的影响，并且采用模糊控制理论对钞票滑移进行补偿，使纸张传输平稳［1］。2006年日本学者Yanabe等人研究了纸张进给系统纸张倾斜的现象，得出倾斜角度和倾斜位置的预测公式，分析得出纸张倾斜的原因是进给轮的两侧压力不平衡，并且摩擦系数和前端拉力也会改变倾斜量［2］。2013年哈尔滨工业大学刘会英等人研究了不同正压力、不同转速下打印机辊轮与纸张之间摩擦系数的变化规律［3，4］。2014年芬兰学者Sorvari等人通过对打印机对辊进纸机构的包胶层进行计算和仿真，分析了进给轮上橡胶层的可压缩性对法向载荷、接触宽度、表面滑移量等的影响［5］。2014年哈尔滨工业大学张美美研究了不同橡胶材料的辊轮与纸张之间摩擦系数的变化规律，利用RecurDyn仿真软件对分纸过程进行建模与仿真并进行相关实验，发现硅橡胶的摩擦系数随转速的增加而减小，丁腈橡胶的摩擦系数随转速的增加而增加［6］。2010年韩国学者Choi等人采用非线性弹簧阻尼并联模型能够很好的反应真实的接触情况，软件Recurdyn采用此算法得到接触力，并用库伦摩擦模型得到接触面的摩擦力［7］。2000年西安交通大学马军星等人对纸张的力学特性进行了研究，基于修正的拉格朗日描述推导了三角形平面壳单元用于几何非线性问题分析时的增量平衡方程，进行了实验验证，证明对纸张静、动态力学特性的研究方法是非常有效的［8］。2000年杨胜军等人研究了纸张在空气中受到空气阻尼而产生的振动，进行了实验验证，证明的模型的适用性［9］。2001年上海交通大学贾丽萍等人对纸张在自重作用下的静动力学特性作了研究，结果表明钞票产生大变形时有较好的计算精度和计算量［10］。2009年张百灵等人研究了空气阻力对钞票运输过程中的影响，进行了纸张传送过程的Recurdyn动力学仿真计算验证了计算方法［11］。2002年西安交通大学陈雪峰等人为解决复印机送纸时振动的问题，采用平面等参元分析纸张纵截面大位移几何非线形，结果优于板壳元［12］。2009年日本学者Uraoka等人为了研究纸张在传输过程中堵塞和滞后的现象，将纸张简化为二维的扭簧-梁模型，研究了纸张初始弯曲角度的影响，发现初始弯曲角度越大，与通道搭接发生碰撞的可能性越大，从而造成堵塞的可能性越大［13］。商业软件Recurdyn是由韩国FunctionBay公司开发出的多体系统动力学仿真软件［7］。它采用相对坐标系运动方程理论和完全递归算法，适合于求解大规模的多体系统动力学问题［14］。通过仿真与实验相对比的方法研究了轮组直径、轮组距离、通道半径以及钞票运送速度对钞票运行的影响。

图1 钞票前端因与轮组碰撞产生的折边Fig.1 The Front End of The Banknotes Is Damaged.

2 模型建立

利用Recurdyn/MTT2D软件建模，仿真模型如图2所示。钞票置于平通道内部，初速度为0。平通道水平放置，通道高度为3mm，中心线与轮组1相切。主动轮顺时针旋转，从动轮由弹簧挤压与主动轮相切，并随其以相同线速度旋转。圆弧通道位于轮组1右侧，轮组2置于圆弧通道另一端，主动轮2与主动轮1以相同速度旋转，以避免速度差产生的影响。

图2 圆弧通道中驱动轮组对钞票影响仿真示意图Fig.2 Simulation of The Influence of Drive Wheel Set on Banknotes in Arc Channel.

钞票在通道内会因重力以及轮组和通道面的挤压造成弯曲，因此钞票弹性模量为仿真过程的重要参数。通过仿真与实验对比钞票挠曲，得到仿真所需的弹性模量。钞票挠曲的实验过程与仿真模型如图3所示，将钞票的长度方向至于圆柱上方，钞票自然下垂，得到钞票尖端距离桌面的距离。利用Recurdyn/MTT2D软件建模，圆弧通道直径为70mm，钞票长度为155mm。将钞票延长度方向离散为20个刚体及19组转动副和扭簧的模型，钞票置于圆柱上方仿真后产生弯曲，读取第一个刚体的与坐标原点的Y方向距离加上通道半径，与实验实测参数对比。通过调整钞票弹性模量使仿真与实验相符，从而得到钞票的弹性模量为3850N/mm2。仿真参数，如表1所示。

表1 模型几何参数Tab.1 Geometric Parameters of Model.

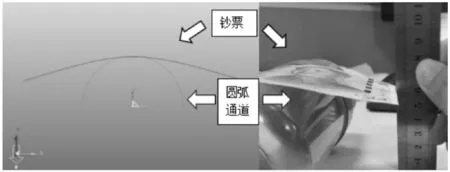
图3 钞票挠曲实验仿真模型Fig.3 Experiments and Simulation Models of Banknote Deflection.

在保证计算精度和计算效率的前提下，将图2所示钞票运动仿真模型中的钞票离散为50个刚体及49组转动副和扭簧，并将由挠曲仿真结果得到的弹性模量用于钞票运动仿真中，得到不同工况下的圆弧通道的驱动轮组对钞票运送的影响。

3 结果与分析

3.1 钞票在通道中运动

钞票在圆弧通道中移动过程。钞票在平通道中静止，被轮组1夹持加速到1000mm/s的速度运行。由于重力和钞票自身的弹性，钞票尾端下落至平通道的下表面。钞票前端接触圆弧通道外壁然后沿着外壁滑行，直至与从动轮2相碰撞后沿着从动轮2外圆下滑至轮组2中间，由两组轮组共同驱动。然后票尾脱离轮组1，沿着圆弧通道外壁移动直至完全脱离轮组2，如图4所示。

从图4可知，钞票在进入圆弧通道时会与通道外壁产生碰撞，以及在接触从动轮2时会发生碰撞，因此需要分析此两个位置的接触力。Recurdyn/MTT2D软件后处理过程可以读取钞票前端的第一个刚性体（Sheetbody1）的接触力（FM_Contact），绘制进入圆弧通道至与从动轮2将碰撞时间段的接触力与时间的曲线，如图5所示。图中可以看出，钞票前端通过轮组1后悬空没有接触力，直至与圆弧通道外壁接触而发生较大的碰撞力，约为0.003N。由于钞票进入圆弧通道的长度增加，轮组1推动钞票使钞票前端与通道面之间的压力下降，所以曲线在碰撞后逐步下降。钞票沿圆弧通道移动至与从动轮2碰撞产生了较大的碰撞力（0.122 N），远大于与通道的碰撞力，造成图1所示的钞票前端的损伤。因此，在圆弧通道中对钞票产生最大撞击力的位置在从动轮2与圆弧通道交接的位置，调整参数减少钞票运送到此时刻的接触力就可以保护钞票免受损伤。

图4 钞票通过圆弧通道过程图Fig.4 The Banknote Passes Through the Arc Channel.

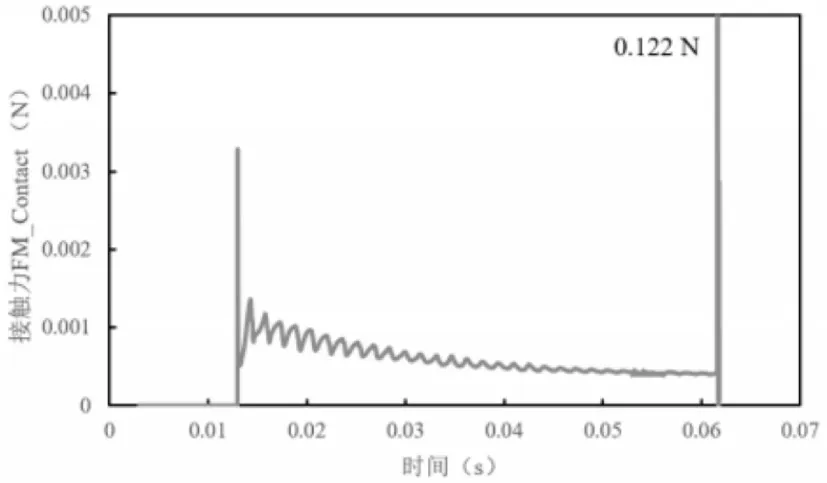
图5 接触力FM_Contact-Sheetbody1随时间变化曲线Fig.5 The Curve of Contact Force FM_Contact-Sheetbody 1.

3.2 从动轮直径的影响

从动轮直径直接影响钞票在圆弧通道中的撞击角度，是分析钞票受力的重要参数，不同从动轮直径所对应的钞票前端第一个刚体的接触力，如表2所示。

表2 不同从动轮直径所对应的钞票前端接触力Tab.2 Contact Forces at the Front End of Banknote with Diameters of Driving Wheels

从表中可以看出，钞票前端的接触力是随从动轮直径的增大而增大的，但超过18mm之后接触力出现大幅下降。通过对仿真过程依次进行分析可知，接触力的增加与浮动轮和钞票碰撞后弹起高度正相关。从动轮直径越小，其质量越小，受力后弹起的高度越大，因此浮动轮对钞票的接触力也就越小。当从动轮直径超过18mm时，从动轮的弹起高度变化较小，但是通道与从动轮的切线夹角变小，造成钞票前端与从动轮切线夹角变小，因此碰撞力大幅下降。因此，虽然选择较小的从动轮可以有效的降低钞票撞击的碰撞力，但是小从动轮质量小，抖动较大。考虑到钞票运送的稳定性，在安装空间允许的情况下，应当选择较大从动轮。

3.3 圆弧通道半径

钞票由于自身拥有一定的弹性，其在圆弧通道中移动时会受到通道外壁的挤压。钞票不同弯曲程度条件下撞击从动轮会产生不同的效果，因此，圆弧通道半径也是重要的优化参数。圆弧通道半径对碰撞力的影响，如表3所示。

表3 不同圆弧通道半径所对应的钞票前端接触力Tab.3 Contact Force of Front End of Banknote with Radius of Arc Channel

如表所示，除了半径为25mm时的接触力较大以外，接触力随圆弧通道半径的增加而增加。通过对仿真过程进行分析发现，半径较小时，钞票发生较大弯曲，并且钞票推理轮组1的距离较短，拥有较高的刚度，所以钞票前端与接触点的压力较大。半径超过30mm以后钞票弯曲程度降低，影响接触力的主要因素变为钞票前端与浮动轮的接触角度。通道半径越大，其与从动轮在交叉点处的夹角越小，即钞票前端与从动轮切线角度越大，则其产生的撞击力也就越大。所以较小圆弧通道半径不仅可以减小设备所占的空间还能降低钞票前端的损伤，但是通道半径不能小于30mm，不然反而会增加钞票的损伤。

3.4 轮组间距

圆弧通道中，两组轮组间的距离可以以圆弧通道的圆心角度来表示，圆心角α越大则表示钞票在通道内运行的距离越远。圆心角与钞票前端接触力之间的关系，如图6～7所示。

图6 圆弧通道两组轮组之间的圆心角Fig.6 Core Angle Between Two Groups of Wheels in The Arc Channel.

由图中可知，圆心角越大则其所对应的钞票前端接触力越小。因为钞票在通道内的动力全部来自与轮组1，轮组1推动钞票的后端，又因为钞票为柔性体，当钞票前端受阻后会发生弯曲。轮组1与轮组2越远，钞票可弯曲的程度越大，所以钞票前端与浮动轮的接触力也就越小，反应为图7所示的曲线下降的趋势。

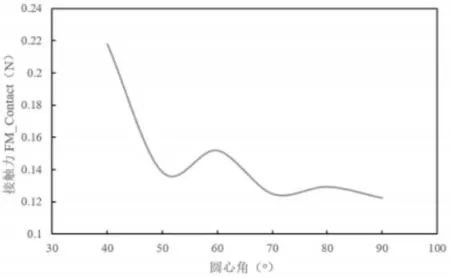
图7 轮组间圆弧通道圆心角与钞票前端接触力之间的关系Fig.7 The Relationship Between Angle of The Arc Channel and Contact Force of Front End of the Banknote.

因此，在设计圆弧通道时应尽量增加两轮组之间的间距，但不要超过钞票宽度保证钞票不会出现两轮组全部脱离的失控状态。

3.5 钞票运行速度

钞票在设备中运行需要进行检伪、计数等操作，不同的操作以及不同的工况需要钞票以不同的速度运行。因此需要分析钞票运行速度对钞票前端受力的影响，如图8所示。

图8 钞票运行速度与钞票前端接触力之间的关系Fig.8 The relationship between the speed of banknote and the contact force of the front end of banknote

钞票在以100mm/s的速度运行的时候，钞票前端的接触力只有0.0012 N。较慢的钞票速度碰撞浮动轮，浮动轮抬起的时间较长，其加速度较小，所以对钞票的接触力就非常小。随着钞票速度的增加，钞票对浮动轮的冲量增加，其接触力大幅度增加。当钞票速度超过1500mm/s后，浮动轮受钞票碰撞迅速抬起，所以不会接触力没有明显的上升。因此，钞票在通道中的移动速度应越小越好。

3.6 从动轮在圆弧通道外侧与内测对比

钞票进入圆弧通道后沿着通道外壁移动，到达从动轮时会与从动轮发生碰撞。当从动轮在通道内侧时，钞票沿外壁移动就会碰撞到主动轮，因此，需要分析钞票碰撞主动轮和从动轮的区别。实线为从动轮在内侧，不同主动轮直径，钞票碰撞主动轮的情况，虚线为从动轮在外侧，不同从动轮直径，钞票碰撞从动轮的情况，如图9所示。

图9 从动轮在圆弧通道内侧和外侧对比Fig.9 Comparisons of Driven Wheels Inside the Arc Passage and Outside the Arc Passage.

钞票前端与主动轮之间的接触力大于与从动轮的接触力，但是其随直径的变化趋势基本相同。因为从动轮没有动力，其运动是来自主动轮的挤压转动。钞票撞击从动轮，从动轮会出现短暂的速度失稳，从而抵消一部分的接触力。而主动轮是以稳定的速度旋转，钞票撞击主动轮时会产生较大损伤。所以为保护钞票，应当尽量将从动轮排布在通道外侧。

4 实验验证

为验证浮动轮与钞票碰撞仿真模型的正确性和有效性，对其进行实验验证。实验采用步进电机驱动主动轮，主动轮直径20mm，外层包胶硬度为60度，从动轮选用不锈钢轴承。圆弧通道采用PC+10%ABS材料加工，并由钣金固定。对通道直径和钞票运动速度进行实验，实验参数，如表4所示。

表4 实验验证参数Tab.4 Experimental Validation Parameters.

实验采用全新百元钞票进行实验。每组实验挑选200张钞票依次在通道里运行10次，然后观察钞票前端状态，如图10所示。第一组实验可以看出，钞票前端出现明显弯折，并且其中部分钞票出现撕破的现象。第二组实验钞票前端情况良好，为出现明显变化。第三组实验钞票前端出现了一定程度的白边，并未折弯，说明其与浮动轮发生了较重的碰撞但不足与破坏钞票。与仿真分析结果相同，说明仿真均有实践意义。

图10 实验验证Fig.10 Experimental Verification.

5 结论

（1）建立了钞票在圆弧通道中运动的仿真模型，通道入口处有一组轮组使钞票加速，在出口处与另一组轮组发生碰撞。

（2）仿真分析了钞票在圆弧通道中的运动过程，和钞票前端在运动过程中的受力，发现钞票前端碰撞出口从动轮的接触力远大于钞票与圆弧通道的接触力。

（3）分析了从动轮直径、圆弧通道半径、轮组间距、钞票运行速度以及从动轮位置对钞票前端碰撞力的影响，发现加大的从动轮直径可以提高钞票运输的稳定性，较小的圆弧通道半径、较大的通道半径会产生较小的碰撞力，钞票运送速度越快其碰撞力越大，将从动轮排布在圆弧通道外侧有助于减小钞票碰撞力。

（4）针对仿真模型进行实验验证，实验结果与仿真结果相符，验证其有效性。