STL模型冗余顶点全域哈希处理算法

李 勇，宋占洋，尚会超，付晓莉

（中原工学院机电学院，河南 郑州451191）

1 引言

STL文件（Stereolithography，光固化立体造型术的缩写）作为一种三维模型数据格式，常用于CAD应用程序，例如快速成型系统中［1-2］。STL格式非常简单，其原理是所有模型的表面都可以看作一个多边形，多边形用一组三角面片进行分割，每个三角面片用一组表示其顶点坐标和法向矢量坐标信息的数据保存到文件中，分割模型的三角面片被随机的存储，彼此之间没有任何邻接关系［3］。

但是在实际应用时，STL格式文件最主要的缺点就是它的存储形式不包含模型表面结构和拓扑关系。在STL文件的生成算法中，每个顶点至少被6个三角形共有，这个共有的顶点坐标被重复存储，造成了大量冗余坐标信息［4］。

在进行模型处理时，需要重构三角网格，建立三角面片之间的拓扑关系。这种拓扑关系的建立是通过对每个顶点找到所有包含这个顶点的三角面片。从给定的三角面片集合中重建三角网格具有很大的复杂性，特别是对所含三角面片数量较多的模型文件［5-6］。

重构三角网格时，必须遍历三角网格上的每个顶点，将他们在一个坐标系中进行排序，删除重复顶点坐标，建立有规律的三角网格和邻接的三角形坐标信息。重构的三角网格中，所有顶点只存储一次，在计算机中执行这种操作的时间复杂度可达O（NlogN），其中N为三角网格中三角面片的个数，如果对于一个106-107量级的三角形面片数量来表达的模型表面，网格重构将会是非常耗时的过程［11］。将哈希算法应用于数据的处理已经在一些研究中进行了应用，其期望时间复杂度为O（1）级。文中介绍一种基于全域哈希算式的模型重构算法，并对其进行理论和实验性质的比较。

2 哈希算法

2.1 哈希算法

哈希表法又称为散列表法，它是直接寻址法的改进算法，既保留了直接寻址法操作数据效率高，又解决了直接寻址法中占用内存空间过大，大量直接寻址表中空间被浪费的问题。其基本思想是：将需要操作的每条数据存储在内存中，每条数据的存储地址都有一个唯一与之相对应的关键字（key），所有需要处理数据的关键字组成一个动态集合S，将S中的每一个元素经过哈希函数运算得到一个函数值，函数值对应的时哈希表中的槽位。

对于哈希算法来说，在进行关键字集合的映射运算时，会存在一个潜在的问题，即不同的关键字，再经过哈希函数的运算后，会被分配到同一个槽位，我们称之为“冲突”。为了解决冲突，在哈希表中引入了链式存储结构，即在发生冲突的槽位中，生成一个数据链表，将冲突数据存储在链表中，链表法的引入解决了冲突的存储问题。常用的哈希函数构建方法有：除法散列法、平方取中算法、乘法散列法、加法散列法等。

对于哈希算法的评价原则是：

（1）哈希运算速度快。

（2）减少冲突的发生。

（3）减小哈希表的装填因子。

理论上不存在一个哈希函数使得关键字集合能够完全独立的分布在哈希表中，但是好的哈希函数应该使哈希运算结果能够尽量满足简单均匀哈希假设：每个数据所对应的关键字都等可能的映射到哈希表中任何一个槽位中，且该映射于其他数据是否已经映射到此槽位无关，满足等可能和独立性要求。

2.2 全域哈希算法

全域哈希算法是哈希函数构建时一种特殊的算法。对于任意一个精心构建的特定数据组的关键字，通过哈希运算可能将全部数据映射到同一个槽中，使得操作时间变为O（n）。任何一个已经选定的哈希函数都会出现这种最坏运算状况，为了针对这种情况发生，在进行哈希运算时，随机的从全域哈希函数集中选择一个独立于数据组的哈希函数，对数据组关键字进行哈希运算，这种随机化的操作，避免了会发生最坏情况的算例。通过全域哈希算法运算，对于任何一个从全域哈希函数集中选出的函数h（x），将数组中n个数据所对应的关键字映射到容量大小为m的哈希函数表中，并用链表法解决冲突，对于任何一个关键字k，其发生冲突的期望次数小于n/m。

3 全域哈希数据冗余处理算法的实现

3.1 已有函数分析

在文献7中，Glassner介绍了三角网格重建的哈希函数算法如式（1）所示。

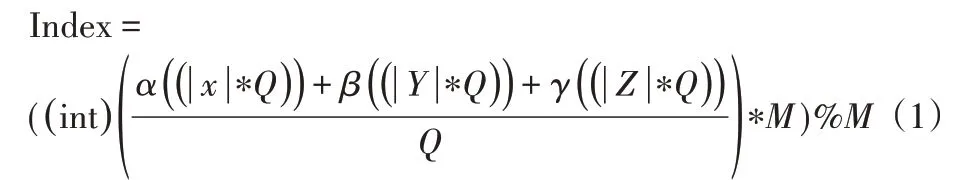
式中：（int）进行数据类型转换，将浮点数小数部分删除；α、β、γ—哈希函数系数，取3、5、7；X、Y、Z是三角面片中顶点的坐标；Q—精度系数，表示取顶点坐标小数点后的位数，例如精度等级取3，Q=103；M—哈希表的大小，通常取2k个，便于快速取余；%—取余操作。

对式（1）进行实验验证，设置Q=103（文献所取），程序运行后，结果如图3所示，得到的链表长度非常大。为了实验算式中所取参数对求解结果的影响，取Q=107进行验证，结果有了很大的改善（如图4）。又通过对哈希函数系数α、β、γ的改变和面片数量不同的模型文件进行实验（图4、图5），证明该函数不仅依赖于顶点坐标精度的求解，也依赖于系数的选取和模型数据量的大小。图3-5为在不同参数和不同数据量模型下哈希表中链表长度图形。通过对上述哈希函数的分析，在算法1函数中，顶点坐标数据精度和系数的选择对于顶点坐标处理结果有很大影响。

图4 算法1链表长度与数量曲线图Fig.4 Algorithm-1 Length and Quantity Graph of Linked List

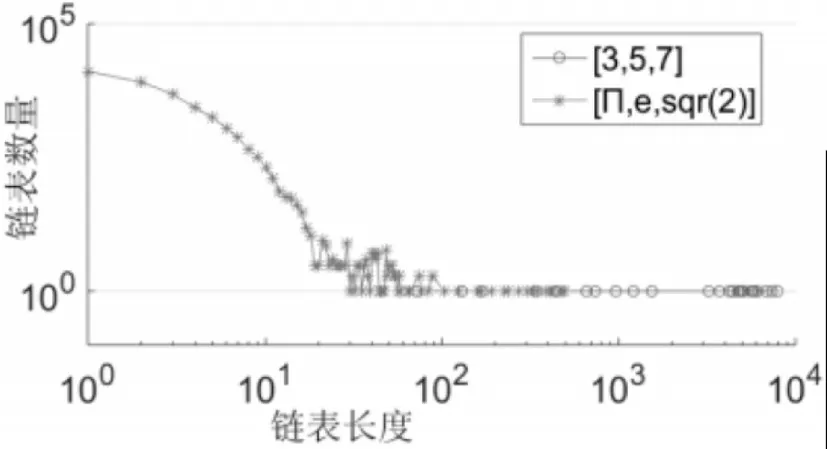
图5 算法1链表长度与数量曲线图Fig.5 Algorithm-1 Length and Quantity Graph of Linked List

3.2 全域哈希算法设计

3.2.1 顶点坐标求和计算

为了改进算法1存在的不足，在原来函数运算的基础上，利用全域哈希函数的构造思想，在系统运行时，根据系统当前运行时间，构造一组随机数列，随机的在数列中先用一个数，用这个数来构造哈希函数，参与哈希运算，该函数为随机函数，避免了静态哈希函数对特定模型计算中，产生大量冲突的问题，用于对模型数据的处理，减少冲突发生的概率，提高哈希运算的效率。

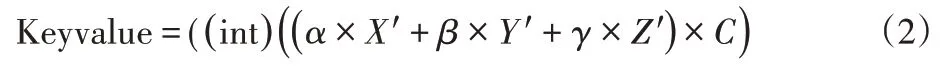
式中:X′、Y′、Z′—顶点的转换坐标；α、β、γ—哈希函数的系数；C—一个比例系数，取232-M，M—哈希表的大小。

3.2.2 坐标变换

如果已知顶点坐标的范围，那么顶点坐标可以利用下列公式转换到（0，1）区间中：

式中：Xmax和Xmin—坐标最大值和最小值，但在实际运算过程中往往是不可知的。对于未知范围的坐标，使用下列公式：

式中：K—一个参数，它决定了这个变换的非线性，K＞0.

通过上面这个公式，可以把X的任意坐标值转换到区间（0，1）中，而不需要为了寻址Xmax和Xmin而遍历整个模型文件，这个公式也可以用于顶点Y轴和Z轴方向的坐标转换。

3.2.3 构造哈希函数

根据求得的值Keyvalue作为这个顶点的键值，利用全域哈希算法，求得其在哈希表中的索引值。

所利用的一种经典全域哈希构造方法，其构造过程如下：将Keyvalue值分解为r+1位，Keyvalue={k0，k1，…，kr}，其中0≤ki≤m-1。分解的思想是把Keyvalue用m进制表示，算法是不断让Keyvalue对m进行取余。ki表示其中的一位，定义k0为最低位。第一次把Keyvalue对m取余，得出第一位，即最低位k0。然后将Keyvalue除以m的商，再用来对m取余，然后再把商除m，依次循环下去，把Keybalue分解为r+1位。哈希集合的选取取决于随机数，随机选取一个数a，将a同样的用m进制表示为r+1位，即a={a0，a1，a2…ar}，其中0≤ai≤m-1。

哈希函数为：

将Keyvalue的每一位与a的每一位相乘之后再相加，然后再对链表长度m取余。将每一个顶点坐标依据此算法进行求解，即可得到每个数据在哈希表中的槽值。其中m为哈希表的长度。

哈希表长度一般取决于需处理模型数据中三角形顶点个数，在STL文件中，每个顶点被存储约为6次，即顶点数为三角形面片数目N的2倍。为了减少处理模型顶点坐标时发生冲突的概率，取装载因子f=0.5，也就意味着链表的长度为模型中三角面片数量的一半。根据计算机内部处理数据的原则，一般取哈希表的长度为质数，即哈希表长度N/4≤m≤N/2，这样可以提高算法的运算效率。

3.3 函数性能测试指标

由于实验测试中涉及到不同的算法，对算法质量进行评价采用以下指标：

（1）链表的平均长度

（2）链表最大长度

（3）检索复杂度—即在对模型文件中顶点坐标数据进行处理时，在链表中检索的总项数。

求上述两个哈希函数的指标值，特性较好的函数指标应得到较小的值。为了比较算法1（Glassner所提出的函数）和算法2（文中所求的哈希函数）的性能，采用以下相对标准来进行比较：

链表平均长度比：用系数ν来表示链表平均长度的比值

链表最大长度比：用系数η来表示链表最大长度的比值

检索复杂度比：检索复杂度计算表示的是在哈希表中检索一个元素所需的时间长度。如果检索链表的长度为i，检索时，链表内所有的元素都倍检索到，我们就需要访问链表i次，当长度为i的链表有Ni个时，那么对这个链表所有访问次数为iNi。

从链表中检索一个顶点有三种可能情况（已确定顶点在哈希表中的槽值）：

（1）链表为空，顶点没有被保存到链表中，那么这次操作所消耗的时间Q1=0；

（2）链表不为空，且顶点也没有被保存到链表中，需要访问链表中所有数据，因此这次操作所消耗的时间Q2=i。

（3）链表不为空，且顶点已经保存到连中，为了找到这个顶点，平均只有一半的链表被检索访问，此次操作的时间为Q3=i/2。

指标三可表示为：

所以：

式中：imax—最大链表长度，i—链表长度，Ni—长度为i的链表的个数，DV—模型中顶点的数量，与以上两个指标相比，指标三能更好的反映函数的质量特性。

我们引入δ表示两个哈希函数检索复杂度的比值：

4 实验结果

利用Visual Stadio软件对算法1和算法2进行C语言编程，对21个顶点数量不同的模型文件进行实验。其中图1和图2是用于测试的典型模型文件。图1是一个下体残肢模型文件，图2文件是一款健身仪器底座模型。表1和表2分别统计了算法1和算法2采用不同参数对这两个模型的运算结果。本实验选取K=10作为系数进行运算分析。

图1 灯罩Fig.1 Lampshade

图2 机器底座Fig.2 Machine Base

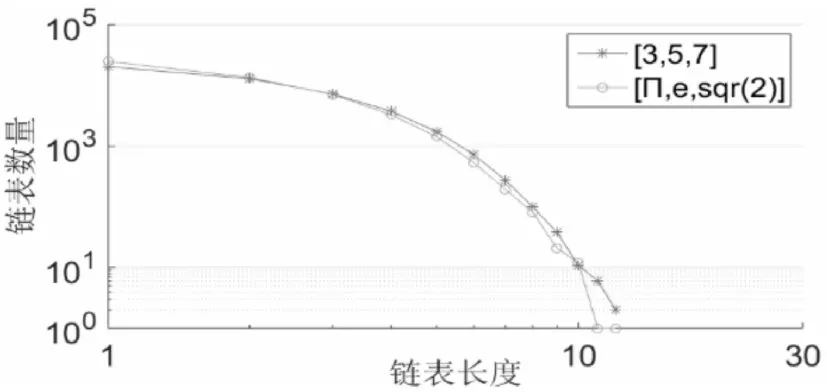
图7 算法2链表长度与数量曲线图Fig.7 Algorithm-2 Length and Quantity Graph of Linked List

算法1运算实验结果分析：在表1和图3、4、5中分别列出了算法1在取不同参数下对不同模型文件进行顶点筛选处理的结果。从以上图表中可以看出，在算法1的处理结果中，最大链表长度和平均链表长度分布情况不稳定，数值较大，在实际的运行中将会消耗大量的运行时间。

表1 算法1取不同参数对不同模型的运算结果Tab.1 The Results of Algorithm-1 for Different Models With Different Parameters

算法2运算实验结果分析：表2和图6、7中分别列出了算法2在取不同参数下对不同模型文件进行顶点筛选处理的结果，链表长度与链表数量的关系图，从图上可以看出，曲线偏差不大，说明α、β、γ的取值对运算结果的影响不大，且链表数量随链表长度的增大而减小，线性程度好。

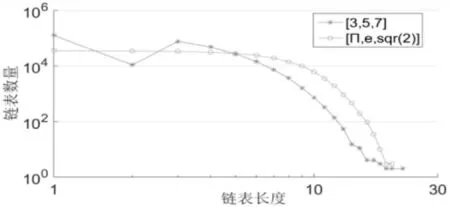
图6 算法2链表长度与数量曲线图Fig.6 Algorithm-2 Length and Quantity Graph of Linked List

表2 算法2取不同参数对不同模型的运算结果Tab.2 The Results of Algorithm-2 for Different Models With Different Parameters

图8为算法1和算法2对不同模型数据处理结果中最大链表长度和三角面片数量的对应关系图，并给出了两种算法下的最佳参数。

图8 最大链表长度与三角面片数量关系图Fig.8 Graph of Relationship Between Maximum Length of Linked List and Number of Triangular Faces

图9为两种算法对不同模型处理结果，从图中可以看出，在对于不同的模型，算法的运算结果各有优劣，但是可以看出算法2在大多数情况下都能得到更好的结果。图10为两种算法对不同数据模型检索复杂度的比值，从图中可以看出，算法2整体上要优于算法1，而且其时间复杂度一直保持在一个稳定的范围内，除去三个异常模型处理结果，可以算出检索复杂度比值的平均值为1.45.

图9 指标ν和指标η与三角面片数量关系图Fig.9 Graph of Relationship Between Indicators ν and η and Number of Triangular Facets

图10 检索复杂度比值与三角面片数量关系图Fig.10 Graph of Relationship Between The Complexity Ratio and The Number of Triangles

从算法1和算法2对21个模型数据的处理结果以及最大链表长度、平均链表长度和检索复杂度三个指标的对比结果可以看出，算法2的三个指标变化率很小。

5 结论

针对在STL模型文件重构拓扑关系中，模型文件顶点重复存储和检索困难等问题，利用全域哈希算法的思想，设计了一个新的哈希函数，并对比已有的哈希函数进行实验验证。可以得出，设计的算法具有以下优点：（1）算法中，所用参数的选取与模型属性无相互关联性。（2）算法运算结果稳定，针对不同模型数据，各项指标变化不大。（3）运算结果更快，特别是对于算法1中参数Q未知或者随机选取的情况下。在算法1中各项参数经过优化选择，算法2的运算结果相对于算法1，其最大链表长度比为65%，平均链表长度比为82.9%，检索复杂度比值为1.45。④运算结果中，链表数量随链表长度的增大而减小。