混凝土泵车臂架可靠度分析

黄会荣，张 希

（西安建筑科技大学机电工程学院，陕西 西安710055）

1 引言

混凝土泵车施工灵活高效，广泛应用在工程建设中，其核心部件是臂架［1］。目前对臂架结构强度的研究是以材料力学为基础，根据材料强度极限采用安全系数法进行校核。王碧琨创建了一个37米泵车臂架模型，并进行了静力分析和模态分析，得到了臂架应力云图和模态振型图，指出了臂架的薄弱地方，并提出了后续的优化方案［2］。朱俊辉采用有限元技术，分析了某款泵车臂架结构的强度和刚度性能，得出了不同工况下臂架的应力分布和变形情况［3］。王斌华等通过力学分析找出了泵车工作时的危险工况和经典工况，并在危险工况下对该泵车整体结构进行了有限元分析［4］。这些研究方法均将设计参数作为常量进行分析，却忽略了各种误差产生的影响。

结构可靠度分析将臂架结构尺寸、材料参数以及载荷等作为设计参数，研究臂架在静力条件下各参数对臂架位移和应力的影响。这种方法将影响臂架位移和应力的参数看作不确定量，研究这些变量对臂架静力分析的影响程度，进而提高臂架设计的准确度和可靠度，达到满足强度又节省材料的目的。本文使用了可靠度分析法，利用APDL语言完成参数化建模，结合PDS模块中的两种计算方法，在置信水平95%的条件下对泵车臂架进行了结构可靠度分析。首先利用蒙特卡罗法得到了臂架结构的可靠度。进一步做了灵敏度分析，以找出影响臂架位移与应力的设计参数。最后使用响应面法分析了两组关联设计参数共同作用下的臂架位移和应力的拟合响应面，为后续臂架结构的设计与改进提供一些参考依据。

2 结构可靠度介绍与分析步骤

2.1 结构可靠度介绍

结构的可靠度是指，结构在规定的时间内与指定的条件下，完成结构预定功能的能力［5］。实际工程中，结构的设计模型不完善、材料属性不真实、施加载荷不精准等均有不确定性，这些因素随机的变化将会影响整个结构的可靠度。为了深入研究结构的可靠度，引入数学方法表述不确定因素和结构可靠度之间的关系，使用概率来表示结构实现预定功能的能力，构建的结构功能函数如下：

式中：Z—结构功能函数；X1,X2,X3,…,Xn—结构可靠度研究中的各个随机不确定因素。

结构功能函数可用图1表示，由图可知，Z＜0时结构失效；Z=0时结构极限状态；Z＞0时结构安全可靠。

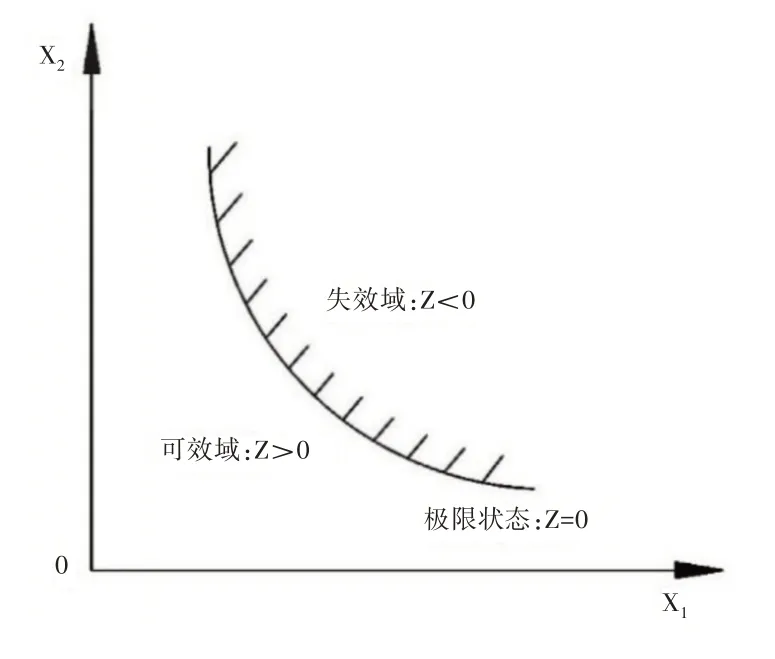
图1 结构极限工作状态Fig.1 The Ultimate Working State of the Structure

2.2 结构可靠度分析步骤

利用PDS模块进行可靠度分析，详细分析步骤如下［6］：

（1）制定分析文件。采用APDL语言在ANSYS中制定分析文件，其顺序如下：①参数化建模，确定臂架三维模型和尺寸，进行参数化编写所有的结构尺寸、弹性模量、密度、载荷等。②划分有限元网格，定义单元类型后对臂架模型进行网络划分，施加固定约束与载荷后进行静力求解。③后处理求解，获得应力与位移结果，为后续分析做准备。

（2）将创建好分析文件导入ANSYS的PDS模块中，进行初始化加载运行。

（3）根据所要研究的臂架模型确定输入和输出参数，并选择选择蒙特卡罗法进行分析，从而得到臂架结构的失效概率和可靠度。

（4）进行灵敏度分析，得到影响臂架应力和位移的设计参数，并找出主要影响参数着重分析。

（5）采用响应面法分析，得到两组关联参数对臂架位移与应力变化的响应面。

3 建立臂架参数化模型

以某型号混凝土泵车臂架为例进行实体建模，选择臂架受力最大的第一节，对其进行适当简化，建立了臂架的全参数化实体模型，并得到图2所示尺寸设计参数图。

图2 臂架尺寸设计参数Fig.2 Dimension Design Parameters of the Boom

这些设计参数可以归为三类，分别是尺寸、材料和载荷参数，整理得到的变量参数，如表1所示。

表1 各个变量设计参数Tab.1 Design Parameters of Each Variable

混凝土泵车臂架使用WELDOX900E型高强度钢制造，其屈服强度为900MPa，弹性模量为2.1×1011Pa，材料密度为7850Kg/m3,泊松比为0.3［7］。单元类型SHELL181壳单元，施加约束为转台与臂架的铰接约束和液压缸与节臂的支撑约束，施加载荷主要是臂架的自重和在泵送过程中管道内混凝土的自重，经计算等效载荷大小为301200N。进行单元网络划分，划分的单元数量为12124，节点数量为24320并施加约束与载荷，如图3所示有限元模型。

图3 臂架网络划分及约束受力Fig.3 Network Division and Constraint Force of the Boom

4 臂架的蒙特卡罗法可靠度分析

4.1 蒙特卡罗法介绍

蒙特卡罗法可以定义几千个输入参数，适合分析大型复杂结构，并且仿真循环次数越多，得到的可靠度分析结果越接近真实值［8］。PDS模块中含有直接蒙特卡罗法和拉丁超立方法（LHS）法两种抽样方法。两者相比，LHS法具有记忆性，可以避免重复抽样，因此选择LHS法。

查阅资料得知众多零部件的几何参数、材料参数、载荷参数等都服从正态分布N(μ,σ2)，工程中材料的强度标准值采用概率分布的0.05。将表1中各变量（泊松比除外）值作为输入参数，将位移与应力变量作为输出参数，如表2所示。

表2 各变量输出参数Tab.2 Output Parameters of Each Variable

4.2 可靠度结果分析

为确定样本是否满足分析要求，查看随机输入参数的直方图。经过1000次循环计算后，选取尺寸变量H1和R3，生成图4所示的抽样直方图。由图可知，这两个参数抽样分布曲线较为平滑，接近正态分布，故此次抽样符合分析条件。

图4 部分参数抽样直方图Fig.4 Sample Histogram of Partial Parameters

查看分析结果，得到臂架位移NMAX平均值为0.191m，臂架应力SMAX平均值是272.41MPa，均在材料许用值内。臂架位移NMAX的累积分布函数如图5（a）所示，应力SMAX的累积分布函数如图5（b）所示。可以看出位移NMAX的可靠度为1，应力SMAX的可靠度也为1，表明该臂架结构可靠，设计合理，符合施工使用要求。

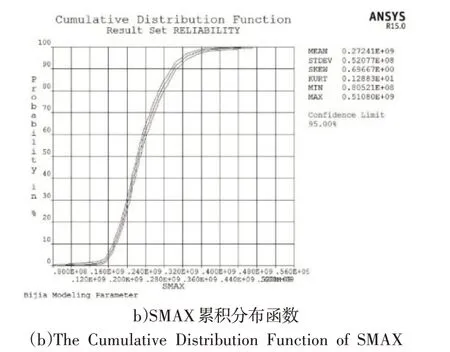
图5 位移和应力累积分布函数图Fig.5 The Cumulative Distribution Function of Displacement and Stress

5 臂架的灵敏度分析

不同的臂架结构设计参数对结构可靠度的影响程度是不一样的。某些参数变化时对可靠度影响较大，称其为敏感因素，因此在结构设计应精确取值，产品制造中应保证加工精度；反之，某些参数的变化对结构可靠度影响十分微弱，称其为不敏感因素，分析时为了提高计算效率，简化结构状态函数，就可以把这些变量当作定值对待［9］。对臂架进行灵敏度分析，为臂架结构设计、加工制造和产品维护给予理论性指导意见。

如图6所示，由NMAX饼图得知，臂架长度H1的灵敏度为正，表明当臂架长度增大时，臂架的位移会显著增大；臂架宽度的一半R1的灵敏度为负，则当臂架宽度增大时，臂架的位移会逐渐减小。其他的结构设计参数如臂架之间铰接点半径R3和宽度H6以及臂架承受压力YL的灵敏度均为正，均会使臂架的位移增大，从而影响混凝土浇筑位置的精确度，因此在结构设计及后续的加工制造只能怪中需着重控制这些参数。还有一些设计参数如臂架液压缸支撑点与铰接点距离H4、材料的弹性模量EZ、臂架高度H2以及臂架板厚度R5的灵敏度均为负，表明适当的增大这些参数的设计值可以达到减小臂架位移的目的，进而提高混凝土的浇筑精度。

图6 位移NMAX的灵敏度Fig.6 Sensitivity of Displacement NMAX

此外，饼图体现了随机输入参数对NMAX参数的影响程度。从影响程度来看，臂架长度H1影响最大，为正向作用；臂架宽度R1影响次之，为负向作用。而这些参数如臂架液压缸支撑点宽度H3和半径R4、臂架与转台铰接点宽度H5和半径R2以及材料密度MD对臂架位移几乎没有影响，因此在分析中可以作为定值以提高分析速度。

如图7所示，从SMAX饼图可以看出，臂架宽度R1增大时，臂架的应力将会显著减小，适当的增加臂架宽度可以达到降低臂架应力的目的；臂架长度H1增大时，臂架的应力将会增大，因此臂架长度不能太长。此外，臂架之间铰接点半径R3和宽度H6、臂架承受位置压力YL以及臂架液压缸支撑点宽度H3的值增大时，臂架承受的应力均会增大；臂架液压缸支撑点半径R4、臂架高度的一半H2以及臂架板厚度R5的值增大时，臂架承受的应力均会减小。

图7 应力SMAX的灵敏度Fig.7 Sensitivity of Stress SMAX

从影响程度来看，臂架宽度R1影响最大，为负向作用；臂架长度H1影响次之，为正向作用。而臂架液压缸支撑点与铰接点距离H4、臂架与转台铰接点宽度H5和半径R2以及材料的弹性模量EZ和密度MD几乎没有影响。

6 臂架的响应面法可靠度分析

6.1 响应面法介绍

响应面法的优势在于在保证分析精度的基础上减少了仿真循环次数。进行响应面法分析首先要进行仿真循环计算以确定分析数据，然后进行回归分析确定近似函数。响应面法中随机输入与输出变量关系式为：

式中：n—随机变量个数，β0—常数项，βi—线性系数，βii—二次项系数。

PDS模块中响应面法分析主要有两种拟合响应面的方法，分别是中心合成法（CCD抽样）和BOX-Behnken矩阵法［10］。本文采用第一种CCD法，此方法原理公式用2N-f表示，N为随机变量的数目。其优势在于会随着N变化会自动改变f的值以保证二次项系数所获得的精度。

6.2 拟合响应面结果分析

进行分析设置后，PDS模块会自动确定求解次数。查看抽样曲线，如图8为臂架长度H1以及臂架之间铰接点半径R3变量的抽样过程图。可以看出本次抽样需要285次，且H1抽样值在8750～9250之间波动，R3抽样值在87.5～92.5之间波动，没有显著的变化，因此样本可信度高。

图8 部分参数抽样曲线Fig.8 Sampling Curves of Partial Parameters

查看分析结果，并与蒙特卡罗法相比较，如表3。可以看出臂架位移NMAX的平均值是0.188m，应力SMAX的平均值是262.03MPa，两种方法分析误差在5%以内，符合要求。

表3 两种分析方法的位移值与应力值比较Tab.3 The Comparison of Displacement and Stress between Two Methods

利用分析计算结果的样本点拟合位移响应面，用RNMAX表示；拟合应力响应面，用RSMAX表示。根据蒙特卡罗法求解的灵敏度分析结果选择影响较大的两组关联参数，一组是臂架长度H1与宽度的一半R1，另一组是臂架之间铰接点宽度H6与半径R3。分别绘制RNMAX和RSMAX的拟合响应面，如图9～图10所示。

对臂架位移值进行分析，如图9（a），随着R1参数根据正态分布随机抽样数值由小增大，响应面中RNMAX的位移值稍微减小；但随着H1抽样数值由小增大，响应面中RNMAX的位移值在逐渐增大，由图知H1越大，RNMAX位移值越大。说明臂架宽度对位移值的影响较小，而臂架长度对位移值的影响较大。分析图9（b），随着H6与R3参数值由小增大，响应面中NMAX的位移值都在增大，说明臂架之间铰接点宽度与半径在受力时均会使臂架的位移增大。与图9（a）相比较，可以看出臂架之间铰接点宽度H6与半径R3对位移值的影响小于臂架长度H1。

图9 关联参数对位移的拟合响应面分析Fig.9 Response surface analysis of displacement fitted by correlation parameters

对臂架应力值进行分析，由图10（a）得，随着R1参数的数值由小增大，响应面中RSMAX的应力值由大变小；但随着H1参数的数值由小增大，响应面中SMAX的应力值经历了由大变小在略微增大的一个过程。可以说明臂宽度对应力值的影响较大，为负向影响；而臂架长度对臂架应力值的影响小于臂架宽度，为正向影响。分析图10（b），随着H6与R3参数值由小增大，响应面中RSMAX的应力值都在逐渐增大。与图10（a）对比，可以看出臂架之间铰接点宽度H6与半径R3对位移值的影响小于臂架宽度R1。铰接点是臂架之间的连接位置，将后续臂架自重简化为集中载荷施加到铰接点，因此该位置的设计参数直接影响臂架之间的连接强度以及臂架位移应力变化情况，需要合理设计。

图10 关联参数对应力的拟合响应面分析Fig.10 Response Surface Analysis of Stress Fitted by Correlation Parameters

7 结论

本文以混凝土泵车臂架的第一部分为例进行了参数化建模，进行静力分析得到了臂架的位移与应力数据，编写了分析文件，对臂架进行了可靠度分析，得到以下结论：

（1）利用蒙特卡罗法进行可靠度分析，得到臂架位移值NMAX的平均值是0.191m，臂架应力值SMAX的平均值是273.62MPa，均在许用范围内。在95%置信水平的条件下，位移值NMAX的可靠度为1，应力值SMAX的可靠度也为1，因此臂架结构设计可靠。

（2）进行灵敏度分析，臂架长度H1对位移值NMAX正向影响最大，臂架宽度的一半R1负向影响次之；臂架节臂宽度的一半R1对应力值SMAX负向影响最大，臂架长度H1正向影响次之；因此在后续臂架设计与改进中，需着重控制这些参数。

（3）使用响应面法分析，得到臂架位移值UMAX的平均值是0.188m，应力值SMAX的平均值是262.03MPa；并与蒙特卡罗法比较，相对误差在5%以内。

（4）进行两组关联参数对臂架位移与应力的拟合响应面分析。在位移分析中臂架长度H1影响最大，为正向作用；臂架宽度R1影响次之，为负向作用；在应力分析中臂架宽度R1影响最大，为负向作用；臂架长度H1影响次之，为正向作用。