基于CFD法预报组合螺旋桨的水动力特性

王声森 刘益平 张丁标 兰艳肖 张迪

摘要：螺旋桨是船舶的主要推进装置，船舶的推进效率、燃料的消耗和排放量是设计的重要指标。随着计算机性能的提高，有限元法作为计算和评估螺旋桨水动力性能的有效方法，能有效的模拟螺旋桨的运行状况，并获得模拟数据。本文基于CFD数值模拟法对螺旋桨进行有限元计算，比较在不同进度系数下，不同湍流模型对螺旋桨水动力性能的影响;研究螺旋桨的桨叶压力及流场的变化趋势;揭示单桨、对转桨和串列桨的运行特性及敞水性能，为后续研究提供理论基础。

关键词：数值模拟;组合螺旋桨;CFD

中图分类号：U664.33

文献标识码：A

1 前言

随着船舶行业的快速发展，螺旋桨的空泡、振动和噪声等问题制约了螺旋桨的发展，提高单桨的效率也出现了瓶颈，为此国内外学者将目标转移到组合螺旋桨的设计和研究[1]。组合螺旋桨的出现，不仅提高了推进效率，而且有效的改善了空泡和振动的发生。因此，越来越多的学者致力于组合螺旋桨的研究，包括串列螺旋桨、对转螺旋桨等。其中，对转螺旋桨安装在旋转方向相反的两个轴上，而串列螺旋桨在同一轴上装有前后两个旋向相同的螺旋桨。组合螺旋桨能加大桨叶面积，减小单位面积的载荷，且后桨能有效的回收前桨的涡流动能，从而提高效率、避免或减轻空化与振动的发生[2-3]。

对传统螺旋桨的研究方法主要是依靠模型实验和理论计算，实验周期长、成本高。采用数值模拟，不仅能节省人力物力，还能有效的模拟出实际螺旋桨的运行状况，因此数值模拟已成为现阶段对船舶水动力性能研究的最重要的方法之一[4]。

本文基于CFD数值模拟对螺旋桨进行有限元计算。首先，在不同进度系数下，分析不同湍流模型对螺旋桨水动力性能的影响规律;同时，研究螺旋桨的桨叶压力及流场的变化趋势，揭示单桨、对转桨和串列桨的运行特性及敞水性能，为后续T作奠定理论基础[3]。

2 控制方程与湍流模型

2.1 控制方程

以船用螺旋桨为研究对象，周围的流体可视为不可压缩流体，即密度p不随时间变化。对于螺旋桨内的不可压缩流体的三维定常流动，通常用RANS方程来表达，其中连续方程和动量方程的表达式如下[3]：

2.2 湍流模型

本文分别采用standard k-ε、RNC k-ε、RSM和SST k-∞4种湍流模型来计算螺旋桨在不同的进速系数下的推力系数Kr、转矩系數Ko和敞水效率η。考虑到螺旋桨模型曲面空间的复杂、流场和流动旋转特性，本文选取SST k-ω湍流模型，因为SST k-ω湍流模型较RSM湍流模型对计算机的性能要求没有那么高，同时能有效真实地反映实际情况，计算速度快、数值精度较高[3-6]。

2.3 螺旋桨计算公式

对螺旋桨通过数值计算得到的结果，应用以下公式计算螺旋桨的推力系数Kr、扭矩系数Ko和敞水效率η[3]：

3 计算模型和网格划分

3.1 计算模型

以某船用螺旋桨为对象，其主要设计参数为：转数n=450 r/min;螺旋桨直径D=300 mm;0.7 R处螺距比为P/D=1.3;叶片数2=4。

为了有效区分组合螺旋桨和单螺旋桨的各种性能，对转螺旋桨和串列螺旋桨均由单桨组合而成。其中，对转螺旋桨的前桨向左旋转，后桨向右旋转;串列螺旋桨前后两桨旋向相同，均为左旋转。图1分别为螺旋桨、对转桨和串列螺旋桨的整体模型示意图。

3.2 网格及计算域

对计算域流场可划分为静止域和旋转域两部分：旋转域为直径1.1 D、长度3D的小网柱体;静止域为长度10D、直径5D的其余部分。

因螺旋桨形状复杂，旋转域因螺旋桨表面曲率较大，因此采用四面体网格划分;静止域因结构规整，采用六面体网格，同时在桨叶和桨榖处进行网格加密，在壁面进行边界层网格处理[2-4]。

对组合螺旋桨进行相同方式进行处理。但组合螺旋桨有两个旋转域，需要通过interior对前后两桨的旋转域进行连接，旋转域和静止域之间的交界面采用interface联接。

4 数值计算与分析

4.1 单螺旋桨敞水性能分析

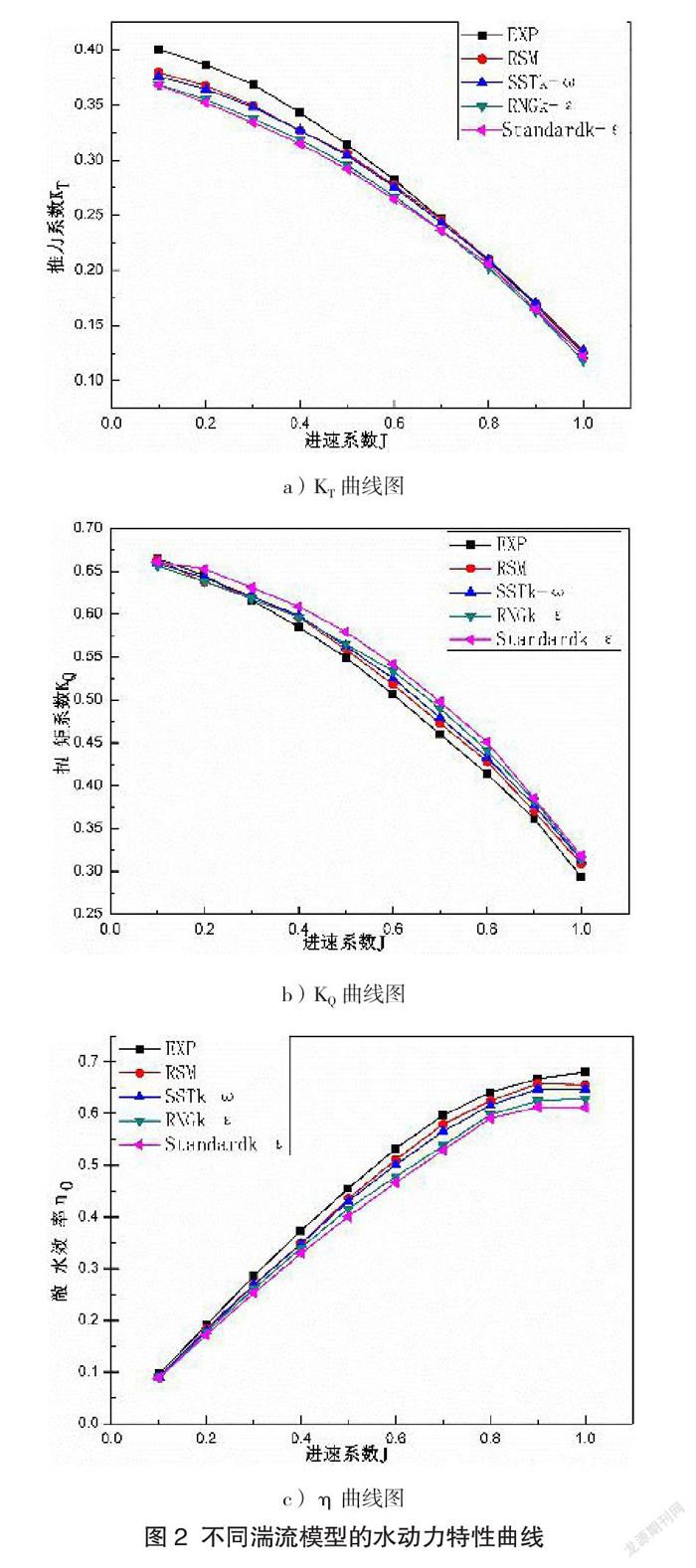
本文选取Standard k-ε、RNC k-ε、RSM和SSTk-∞4种湍流模型进行数值计算。螺旋桨的转速为450r/min，在进速系数0.1-1.0范围内计算的数值结果与实验值相比较，并绘制出在不同湍流模型的水动力性能曲线图，如图2所示。

（1）从Kr和Ko曲线图可知：4种湍流模型得出的KT与实验值误差较小，当J过小或者过大时，误差增大;10Ko随着J逐渐增大，而模拟计算的Ko与实验值误差与J成正比。总体上说，RSM湍流模拟效果与实验相吻合，Standard k-ε湍流模型与实验误差较大;

（2）从η曲线图可看出：实验值均大于湍流模型的计算值;在不同J值下，RSM湍流模型和SST k-ω湍流模型邯曲线与实验值相吻合且精度高。

综上分析可得，与实验值的敞水效率吻合度最好的是RSM和SST k-ω湍流模型，但RSM湍流模型对计算机的配置和运行性能的要求非常高，同时计算所花费的时间长，因此最佳湍流模型选择SST k-ω湍流模型。

4.2 对转螺旋桨数值验证

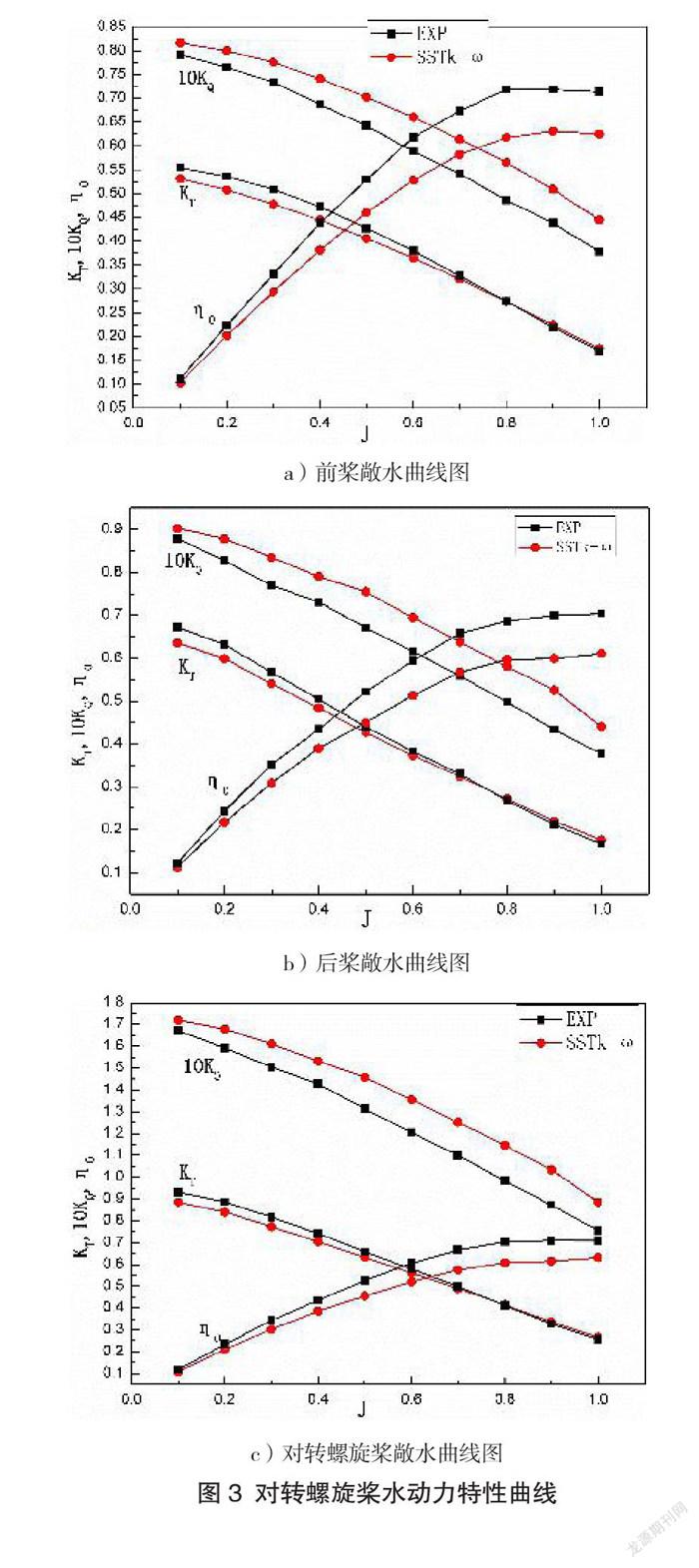
对转螺旋桨的前、后桨扭矩大小相当，旋转方向相反，转速均为450 r/min。基于SST k-ω湍流模型，进速系数J在0.1-1.0之间对转桨进行数值模拟，并绘制数值模拟和实验数据的水动力特性曲线，如图3所示。由图3可知，对转桨前、后桨的Kr曲线和Ko曲线与实验值均相吻合，且10Ko随着J的增大而减小。经过分析可知：后桨受前桨尾流的影响，使得在同一进度系数J下，前桨Ko的误差小于后桨的误差。

从图3c）可以看出：对转螺旋桨的推力系数Kr总体模拟效果都比较好，但10Ko的误差随着J的增大而增大，整体数据均大于实验值，而效率η均小于实验值。

由上可知，基于CFD数值模拟得出的结果与实验值吻合度较高，且满足精度要求。

4.3 串列螺旋桨数值验证

串列螺旋桨前、后两桨的旋转方向相同，且转速也均为450 r/min。基于SST k-ω湍流模型在进速系数J为0.2-1.0的范围进行数值计算，并将得到的结果绘制水动力特性曲线，同时与实验值进行比较，如图4所示：

从图4可以看出：在进速系数J=0.2-1.0范围内，串列螺旋桨的KT曲线、KQ曲线和η曲线的计算值和实验值的变化趋势基本吻合。其中，数值计算得到的KT和η小于实验值，但10KQ值大于实验值，同时从图中可以看出，KT、KQ和η的误差与进速系数J成正比关系，最终结果与实验值吻合度较高，验证了数值模拟方案的可行性。

4.4 组合桨数值验证

选取普通螺旋桨、对转桨和串列桨进行数值计算，按其结果绘制功率系数水动力特性曲线，如图5所示。

由图5可知：对转螺旋桨和串列螺旋桨的效率比单桨的效率高。其中，对转螺旋桨的效率最高，串列螺旋桨次之。在BP=6-255范围内，对转螺旋桨比普通螺旋桨效率提高了7.28%-15.07%，串列螺旋桨比对转螺旋桨效率提高了2.68%-9.79%。

4.5 螺旋桨尾流分析

采用CFD数值计算模拟方法，能真实有效地反应出螺旋桨处的流场情况。为了更清晰的分析单桨和组合桨的尾流情况，选取同一进度系数J=0.7进行分析，如图6所示。

由图6可知：单螺旋桨的尾流外径大于螺旋桨的直径，而组合螺旋桨尾流外径小于螺旋桨的直径;单桨尾流直径与进度系数成正比关系，而组合桨前、后桨相互影响，其后桨吸收前桨的轴流速度与涡流能量，使得尾流外径小于螺旋桨的直径，组合螺旋桨能有效提高螺旋桨的性能与能量的利用率。

5 结论

本文基于CFD数值模拟对螺旋桨进行有限元计算.首先，在不同进度系数下，分析不同湍流模型对螺旋桨水动力性能的影响规律，同时，研究螺旋桨的桨叶压力及流场的变化趋势，揭示单桨、对转桨和串列桨的运行特性及敞水性能，得出以下结论：

（1）采用4种湍流模型对单螺旋桨进行有限元计算，RSM湍流模型和SST k-ω湍流模型表现出明显的优势，说明有限元计算对分析螺旋桨的水动力特性具有可行性和准确性;

（2）通过对单桨和组合桨的数值模拟结果进行分析，在功率系数相同的条件下，组合螺旋桨其敞水效率与单桨相比，体现出明显的优势;

（3）通过对尾流分布分析可知：对于组合桨而言，后桨能有效的吸收前桨的轴向速度和涡流能量，同时切向速度对流体的影响减小，从而流过螺旋桨桨叶的动量增加，使得前桨的尾流外径减小，螺旋桨的推力也随之增加，提高了对转螺旋桨推进性能;同时，组合螺旋桨负荷较轻，在一定程度上减少了振动和噪声。

参考文献

[1]楊美红，李铁骊，胡俊明，林焰等.基于CFD法的对转螺旋桨敞水性能参数匹配研究[J]船舶1。程，2016，39（ ll）：42-46.

[2]王国强，董世汤.船舶螺旋桨理论与应用[M].哈尔滨：哈尔滨]一程大学出版社，2005：383-396.

[3]王声森.基于CFD的某船对转桨侧推器的性能预测[D].江苏科技大学，2019.

[4]胡俊明，李铁骊，林焰，纪卓尚等.基于RANS法的B系列对转螺桨旋敞水性能数值模拟[J].大连理]‘大学学报，2017，57（2）：148-156

[5]王展智，熊鹰，齐万江.对转螺旋桨敞水性能数值预报[J]华中科技大学学报，2012，40（ 11）：77-80.

[6]曾攀.有限元分析基础教程[M].北京：清华大学出版社，2008.