探究数学模型 促进深度学习
冯红芸

摘 要:空间观念、推理能力、刻画图形模型是实施“图形与几何”领域教学的核心理念。文章以“认识三角形”为例,尝试在教学中怎样引导学生在刻画图形模型的基础上,发展空间观念和推理能力,从而对学生形成模型思想方面进行探究。
关键词:小学数学;空间观念;深度学习;模型思想
人教版《义务教育教科书·数学》四年级下册“认识三角形”是“三角形”单元的起始课,学生之前已经对三角形和三角形的高有了初步感知,本节课要认识三角形的特征、三角形的构成要素,并掌握画三角形高的方法,在操作、想象、联系情境解决问题的过程中,引导学生从形的方面加深对周围事物的认识,发展学生的空间观念和几何直观,构建数学模型思想。
数学模型是用数学语言概括地或近似地描述现实世界事物的特征、数量关系和空间形式的一种数学结构。从广义角度讲,数学的概念、定理、规律、法则、公式、性质、数量关系式、图表、程序等都是数学模型。在小学数学教材中,数学模型无处不在。小学生学习数学知识的过程,实际上就是对一系列数学模型的理解、把握的过程。
一、创新教学模式,引导深度学习
学生的数学学习活动应当是一个主动、活泼、生动和富有个性的过程,让学生在进行探究性学习的过程中,科学、合理、有效地建立数学模型。在“认识三角形”一课的教学中,教师创设了“蚂蚁过马路,怎样爬行距离最短”的问题情境。
1. 动手操作内化知识,引导理性思维
《义务教育数学课程标准(2011年版)》(以下简称《标准》)指出,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,进而使学生获得对数学理解的同时,在思维能力、情感态度与价值观等多方面得到进步和发展。
教学片断1:初步感知三角形的高。
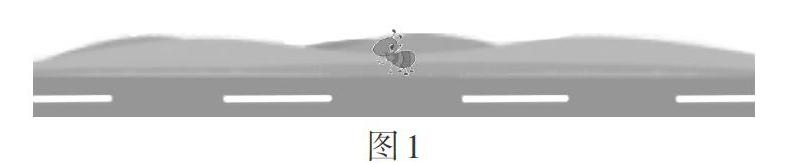
课件出示问题情境:如图1,一只蚂蚁要过到马路对面去。
师:这时候,你们看到三角形了吗?
生:看到了,将蚂蚁看成一个点,马路看成一条线段,连起来就形成一个三角形了。
教师在课件中完善三角形。
师:蚂蚁怎样爬,路程最短?你赞同哪种选项?
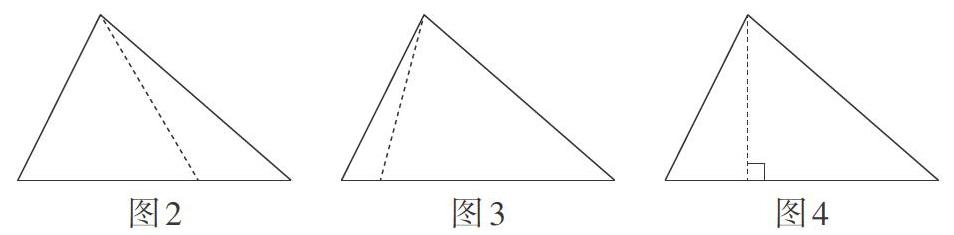
如图2 ~ 图4,课件出示以下三种不同的选项。
生1:第三种情况蚂蚁爬行最短,因为第三种是垂直的,其他两种是斜的。
师:第三条是不是垂直线段?
生2:用三角尺的直角比一比就知道。
师:你会比吗?
生2径直走向黑板,一边用手在黑板上比,一边说:从蚂蚁这里开始,画出一条到马路的垂直线段。说完后,生2先是看向教师,教师又示意他问其他同学,大家有的点头,有的说“不对”。
师:大家意见不统一,到底应该怎么比?
教师话音刚落,表示不赞成意见的生3走向黑板,拿起三角尺,用三角尺的直角和图中的直角进行重合,这一条就是垂直线段。
师:你是怎样比的?
生3:找到三角尺的直角,一条直角边和马路对齐,看看蚂蚁爬的这条路会不会与另一条直角边对齐,这里是对齐的。
师:看来只靠观察还不够,需要借助工具才行。现在能不能判断这一条是不是垂直线段?
学生都同意了。
教师在大家统一认识后,及时梳理:要知道蚂蚁爬行的最短路程,可以把蚂蚁看成一个点,马路看成一条线段,从这个点向线段画一条垂直线段,这条线段的长度就是蚂蚁爬行的最短距离。
画三角形的高是需要学生掌握的操作技能,也是以前学习的“点到直线的距离”的应用与延伸。因此,教师通过创设“蚂蚁过马路,怎样爬行距离最短?”的问题情境,接着从情境中抽象出图形,以问题“第三个选项是不是垂直线段?”“你会比吗?”引领学生复习旧知识,真正掌握用三角尺的直角画垂直线段的技能,为接下来画三角形的高做充分的准备。
在此环节中,学生一开始选择第三个选项是蚂蚁爬行的最短距离,依靠的是观察和猜想,所以教师引导学生用三角尺判断垂直线段的操作活动就特别有意义了。动手操作的价值是可以对通过观察得到的猜想进行验证,通过“说一说你是怎样比的?”有意识地将盲目而浅显的操作变得理性而细致,训练学生的理性思维,引发学生进行深度思考。
2. 动静结合梯度设问,引发深度学习
教学片断2:理解同底等高的三角形。
师:现在蚂蚁向右平移一段距离后,再去对面的马路,要怎样爬行距离才会最短呢?
生4:蚂蚁和马路也形成一个三角形,爬行的最短距离还是从蚂蚁出发,向马路画一条高,它沿着这条高爬行,就是最短距离。
生5:和蚂蚁在第一个点爬行的距离相等。
师:蚂蚁和马路之间的距离是15米,如果要使距离保持不变,蚂蚁还可以在哪个位置?指一指。
学生心中都有了答案,跃跃欲试,抢着要上黑板前面来指。
隨着学生确定了蚂蚁的位置时,教师课件直观展示出一个新的三角形。
教师继续追问:蚂蚁还可以在哪个位置?
生6:蚂蚁还可以在这里,还可以在这里,这里。
学生一边说,手一边在线上左右移动。
教师课件呈现不同的三角形。
生6:只要蚂蚁在上面这条线上的任何位置,到马路的最短距离都是15米。
师:蚂蚁停留的位置不同,为什么蚂蚁到马路的最短距离却是相同的?
生7:因为从蚂蚁到马路画的垂直线段都一样长。
师:大家发现了什么?
生8:这些三角形的高相等。
生9:蚂蚁向左或者向右爬行的线和马路是互相平行的。
生10:这些三角形都是同一条底。
师:是的,这些是同底等高的三角形。
对于三角形高的认识,前面还是侧重在画高的步骤和操作技能方面,此环节的设计旨在引导学生从动态的角度认识三角形的高,既包括“点到直线的距离”与“三角形高”的新、旧知识之间的转化,也包括现实生活与抽象图形之间的转化。
教师的教学改变直接示范画高或者课件演示画高的方法,而是把图形的认识与图形的变换结合在一起认识高,才会出现课堂上学生的手在蚂蚁爬行的那条线上左右移动的画面,才能听到学生用自己的语言解释并推理“平行线之间,垂线段最短”“平行线之间,垂线段处处相等”。苏霍姆林斯基曾经说过,每一个儿童的思维发展都有其独特的道路,每一个儿童的聪明才智都各有各的特点。学生灵动的双眸,跳跃的思维,坚定的眼神,是多么生动和诱人,带给教师巨大的动力和满满的成就感。
二、重视概念本真,构建模型思想
《标准》指出,空间观念主要是指根据物体特征抽象出几何图形,根据几何图形想象出所描述的实际物体;想象出物体的方位和相互之间的位置关系;描述图形的运动和变化;依据语言的描述画出图形等。
1. 去非存本,注重概念内涵
教学片断3:概括三角形的定义。
师:接下来画一个三角形,画三角形之前,先想象一下,你想画一个怎样的三角形。
教师展示收集来的学生按照不同位置画的三角形。
师:一起来看看这几名学生画的三角形,这些三角形一样吗?它们有什么共同点?
生11:这些三角形不一样,有的大,有的小。
生12:有的三角形是平的,有的三角形是歪的,还有一个是倒着的。
教室里顿时发出了笑声。
生13:相同的地方是都是由3条边围成的。
教师强调这3条边是3条线段,并板书:由三条线段围成。
教学片断4:转动图形,体会高的数学意义。
学生已经掌握了画三角形高的方法,教师课件出示转动前后的图形,如图5所示。
师:转动后,AD还是BC边上的高吗?
生:是。
师:为什么?
生14:因为高没变。无论三角形平着放,还是歪着放,都是那条高。
当说到三角形歪着放时,生14还把手和身子也跟着歪起来。
师:仔细对比,这个三角形旋转前后的底和高,什么变了?什么没变?
生15:三角形放的方向变了,但还是那条高。底没变,所以高也没变。
生16:都是画点A到BC边的垂直线段,和三角形摆放的位置没有关系。
四年级学生已经具备了一定的抽象思维能力,教师引导学生在比较抽象的水平上认识三角形和三角形的高,并进行探索。学生个性化地画三角形,观察和对比不同形状、不同摆放方向的三角形,并抽象出三角形的本质特征;通过比较转动前后三角形的高,帮助学生巩固三角形高的数学意义。学生积极参与各种形式的实践活动,而且对活动过程和结果进行判断分析,促使学生多角度、多元化、多维度地认识和理解图形的数学意义,建构模型。
2. 借助想象,构建数学模型
教学片断5:从3个顶点想象三角形。
师:这是用小棒摆的三角形,现在把三角形的3个顶点用圆形磁铁代替,移开小棒,现在你还能看到三角形吗?
生:能。
师:隐藏了什么?
生17:隐藏了3条边,3个角。
师:隐藏的部分在哪儿?
生17:在我的脑子里。
师:只有3个顶点,看不到完整的三角形,隐藏的部分可以想象,3条边、3个角是学生想象出来的,你们的想象力真强。
教学片断6:从一个顶点和一条边想象三角形。
教师再次出示课件:这是蚂蚁,这是对面的马路。
师:你们能看到三角形吗?
生18:能,把蚂蚁看成三角形的一个顶点,马路看成一条边,三角形就形成了。
生19:有3个顶点就可以想象出一个三角形,有一个顶点和一条边也可以想象出一个三角形。
生20:没有的顶点和边都可以放在脑子里。
当看到一个实物时,能想象出它所对应的平面图形;反过来,当看到某个图形时,能想象出它所对应的几何体或实物的形状,想象物体或图形的运动变化,并且可以表达出图形。在观察、对比、想象、分析的过程中,学生的空间观念得到培养,三角形的模型也已经深深地印在了学生的脑海中,使学生真正体会了图形的含义。
3. 沟通联系,发展空间观念
教学片断7:将平行四边形、梯形、三角形的高联系起来。
教师课件出示[?]ABCD,并从顶点D画高,如图6所示。
师:点D作平移运动,其他的顶点都不动,试想一下会变成什么图形?
生21:形成的是一个梯形。
生22:我认为点D向左平移会变成梯形。
师:生22的回答还说明了点D的平移方向,更加具体了。
课件随着学生的回答,点D向左平移,形成梯形。话音刚落,就有学生立刻站起来补充。
生23:向右平移也会变成梯形。
教室里马上出现“咦”“怎么会”等质疑的声音。
教师这时并没有立刻否定,而是把目光投向生23,静静地等待他去答疑。
生23直接走到讲台前模拟,说:如果点D向左平移,形成的梯形是上短下长的;如果点D向右平移,形成的梯形是上长下短的。模拟完,看了看大家,说:不是吗?
此时,学生恍然大悟,没有想过点D向右平移的情况,思维定势地想象点D向左平移,不禁佩服生23的空间想象能力和缜密的思维。
师:梯形的高和平行四边形的高有什么关系?
生24:梯形的高和平行四边形的高相等。
师:继续平移点D,还会形成我们认识过的什么图形?
生25:三角形。
生26:当点D和点A重合时,就是三角形。
师:此时三角形的高、平行四边形的高和梯形的高有什么关系?
生26:它们的高都相等。
生27:它们是同底等高的图形,与前面学习的同底等高的三角形是一样的。
教师巧妙设计,将平行四边形、梯形、三角形的高放在同一个问题情境中,鼓励学生将观察、操作、想象、推理、表达相结合,沟通三种不同图形的高,借助几何直观把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,促进学生思维的发展,养成有条理思考和表达的习惯。
综观本节课,创设情境,以问题为起点实現了生活情境与数学知识之间的无缝对接;动静结合转换,加强新、旧知识之间的联系,引导学生深度学习。在学习如何刻画图形的基础上,发展空间观念和推理能力,从而形成模型思想。
基金项目:江西省教育科学“十三五”规划2020年度普通类一般课题——深度学习视角下小学四年级学生模型思想的教学研究(20PTYB105)。
参考文献:
[1]王永春. 小学数学与数学思想方法[M]. 上海:华东师范大学出版社,2014.
[2]中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.

