2021 年新高考全国数学卷导数试题分析与探究

李海北

（厦门双十中学，福建 厦门 361009）

2021 年教育部考试中心共命制了两套不分文理的新高考数学试卷，两套试卷的压轴题都是导数应用的试题，体现了对函数主线的重点考查.导数试题除了考查常规的函数单调性外，重点考查了函数零点个数和函数极值点偏移问题.

一、函数零点个数问题

研究函数f(x)的零点个数，一般是先确定f(x)的单调区间.如果f(x)在区间D 内单调，且在区间D 内存在x1、x2，满足f(x1)＜0,f(x2)＞0，那么f(x)在区间D内有唯一零点.而对于含参数的函数f(x)，除了可以直观判断的一些特殊点外，要在区间D 内直接找到x1和x2常常是很困难的.如果将f(x)中的指数函数或对数函数放缩为幂函数，并保持放缩后的新函数在区间端点的极限不变，再通过放缩后的函数找“点”，难度就大大降低了.

不难证明下列不等式，它们可用于函数的放缩.

依此类推，可以得到更多的不等式.当然，在解答题的求解过程中，用这些不等式必须先给出证明.

例1（2021 年新高考全国Ⅱ卷第22 题）已知函数f(x)=(x-1)ex-ax2+b.

（1）讨论函数f(x)的单调性；

（2）从下面两个条件中选一个，证明：f(x)有一个零点.

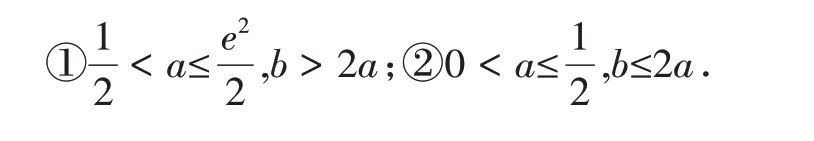
分析与探究第（1）题是常规题.对于第（2）题，若选①，由（1）知，f(x)的增区间是(-∞,0)，(ln 2a,+∞)，减区间是(0,ln 2a).

因为b＞2a＞1，所以f(0)=-1+b＞0（x=0 是可以看出一个特殊点）.要证明f(x)有一个零点，一是要证明f(x)的极小值f(ln 2a) ＞0，二是要找到一个x0∈(-∞,0)，满足f(x0)＜0.

f(ln 2a)=(ln 2a-1)·2a-a·(ln 2a)2+b＞2a·ln 2a-2a-a·(ln 2a)2+2a=a·ln 2a·(2-ln 2a)≥0.

当x→-∞时，对f(x) 的值起主要作用的是-ax2→-∞，而(x-1)ex→0-，可以把它略去.即当x∈(-∞,0)时，(x-1)ex＜0，f(x) ＜-ax2+b.

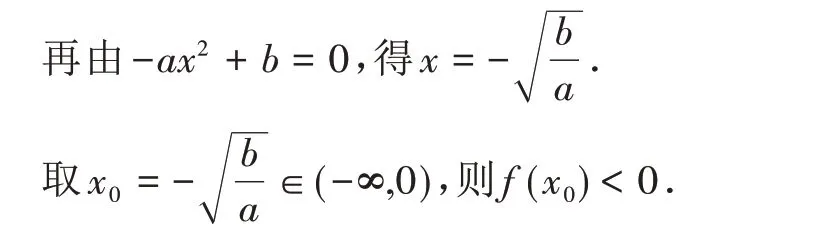
若选②，证明的难点仍然是找到一个x0∈(0,+∞)满足f(x0)＞0.

注意到当x→+∞时，(x-1)ex要远比ax2大，可以考虑将ex缩小为xn，并确保(x-1)xn要远比ax2大，所以x＞1 且n=2 即可.

当x＞1 时，ex＞x2，

f(x) ＞(x-1)x2-ax2=x2(x-1-a)+b，

当x≥2+a时，x2＞1，f(x) ＞x-1-a+b.

取x0=max{2+a,1+a-b}∈(0,+∞)，则f(x0)＞0.

例2（2021 年新高考全国Ⅰ卷第7 题）若过点(a,b)可以作曲线y=ex的两条切线，则

A.eb＜aB.ea＜bC.0 ＜a＜ebD.0 ＜b＜ea

分析与探究本题的实质也是零点个数问题.

设切点为(x0,ex0)，则切线方程为y-ex0=ex0(x-x0).因为切线过点(a,b)，所以b-ex0=ex0(a-x0)，即(x0-a-1)ex0+b=0.

于是可以作两线切线的充要条件是：

函数h(x)=(x-a-a)ex+b恰有两个零点.

因为h′(x)=(x-a)ex，所以h(x)在(-∞,a)上递减，在(a,+∞)上递增.

h(x)极小值=h(a)=-ea+b＜0，即b＜ea.

下面证明当0 ＜b＜ex时函数h(x)恰有两个零点.

可以看出，h(a+1)=b＞0，h(x)在(a,+∞)内有唯一零点.

当x→-∞时，(x-a-1)ex→0-，h(x) →b＞0.但要证明，还是要找到一个x1∈(-∞,a)，满足h(x1)＞0.

作为选择题，如果学生清楚切线的定义，理解当割线的两个交点无限接近时，割线无限趋近的确定位置就是切线，那就可以不必通过运算推理，结合图形就能得到点(a,b)在曲线y=ex与x轴之间.

近年高考常考查函数零点的个数问题，其难点也都是如何找“点”.下面就近年一些高考试题求解过程中涉及找“点”的部分说明如何先放缩再找“点”.

例3（源自2016 年新课标全国Ⅰ卷理第21 题）已知函数f(x)=(x-2)ex=a(x-1)2.当a＞0 时，证明：存在x1∈(-∞,1)，f(x1)＞0；当a＜0 时，证明：存在x2∈(1,+∞)，f(x2)＞0.

分析与深究当a＞0,x＜0 时，ex＜0，(x-2)e3＞x-2，所 以f(x) ＞x-2+a(x-1)2=ax2-2ax=a+x-2 ＞ax2+x-2.

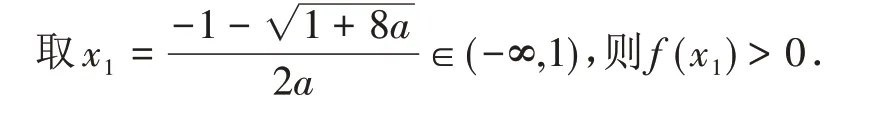
当a＜0,x≥3 时，ex＞x2，

所以f(x) ＞(x-2)x2+a(x-1)2＞(x-2)x2+ax2=x2(x-2-a).

取x2=max{3,2-a}∈(1,+∞)，则f(x2)＞0.

例4（源自2017 年新课标全国Ⅰ卷理第21 题）已知0 ＜a＜1，函数f(x)=ae2x+(a-2)ex-x.

证明：存在x1∈(-∞,-lna)，f(x1)＞0；存在，x2∈(-lna,+∞),f(x2)＞0.

则f(x2)＞ex2-x2＞0.

例5（源自2018 年新课标全国Ⅱ卷理第21 题）已知函数证明存在x0∈(2,∞)，f(x0)＞0.

分析与探究当x≥5 时，

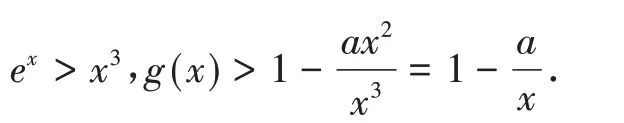
取x0=max{5,a}∈(2,+∞)，则g(x0)＞0

例6（源自2021 年高考全国甲卷理第21 题）已知a＞1，函数g(x)=a·lnx-lna·x.证 明：存 在，g(x0)＜0.

分析与探究因为lna·x关于x是一次的，所以要将a·lnx放大为关于x的次数小于1 的幂函数，以确保lna·x仍起主要作用.

二、函数极值点的偏移问题

例7（2021 年新高考全国Ⅰ卷第22 题）已知函数.

（1）讨论f(x)的单调性；

（2）设a，b为两个不相等的正数，且blna-alnb=a-b，证明：

分析与探究第（1）题是容易题，f(x)的增区间是(0,1)，减区间是(1,+∞).第（2）题是难题，难点一是条件等式变形，难点二是不等式的证明.

将条件等式两边同除ab，并移项得

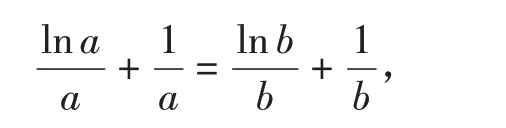
结合f(x)的表达式，可进一步化为

左边不等式的证明，在往年的高考题中多次出现，被称为“极值点偏移”问题，一般用构造函数法证明.如2010 年天津卷理第21 题、2016 年新课标全国I卷理第21 题.

对于右边的不等式，如果也用证明左边不等式的方法，可有如下思路：

由第（1）题知，f(x)在(0,1)内递增，在(1,+∞)内递 减，f(e)=0，不妨设0 ＜x1＜1 ＜x2＜e，则x2,ex1∈(1,+∞).

x1+x2＜e⇔x2＜3-x1⇔f(x2)＞(e-x1)⇔f(x1)＞f(e-x1).

设F(x)=f(x)-f(e-x)，0 ＜x＜1，只要证明F(x) ＞0.

由F′(x)=-ln[x(e-x)]=0，得

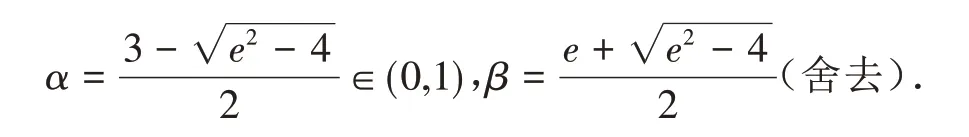
易知f(x)在(0,α)内递增，在(α,1)内递减.

因为f(x)在(1,+∞)内递减，

所以F(1)=f(1)-f(e-1) ＞0.

但因F(x)在x=0 处没有意义，在高中阶段无法严谨说明当x∈(0,α)时，F(x) ＞0.

如下证法很好地避开了函数在x=0 处的值.

由0 ＜x1＜1，得1-lnx1，x1(1-lnx1)＞x1，即f(x1)＞x1⇔f(x2)＞x1.

所以x1+x2＜x2+f(x2)=2x2-x2lnx2.

设h(x)=2x-xlnx，1 ＜x＜e.

则h′(x)=1-lnx＞0，h(x)在(1,e)内递增.

所以h(x2)＜h(e)=3，这就证明了x1+x2＜e.

如果教师将这样的证法讲给学生，学生只会感叹太精彩、太巧妙，但想不到、记不住，下次遇见仍然不会，更别说举一反三了.要避免只给学生讲解法，而要让学生体会并明白解法的背景和构思的理由.

下面从函数图象上对x1+x2给出一个直观的解释.

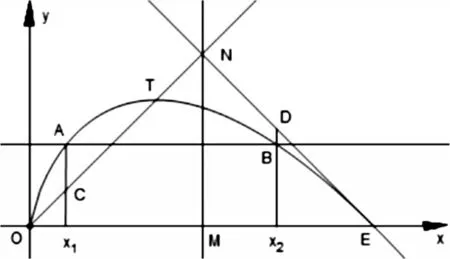
图1

设T 为图象的顶点，MN 为线段OE 的中垂线，作直线OT、直线OT 关于直线MN 对称的直线EN.直线ON 的方程是y=x，直线EN 的方程是y=-x+e.从图中可以看出，

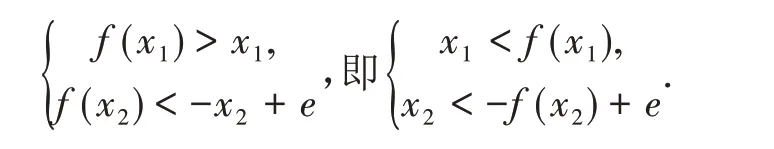
因为f(x1)=f(x20，将以上两式相加即得

x1+x2=e.

这就很自然地引导学生去证明f(x1)＞x1和f(x2)+x2＜e.

综上，文章通过新高考全国数学卷函数零点个数及极值点偏移问题的分析与探究，提出了先将超越函数放缩成幂函数及“以直代曲”构造函数的思路，并通过近年全国高考试题的类比，找到了解答此类问题的通性通法，优势是做一题得一法会一类的目的，避免“题海战术”.