三角转子发动机端面密封条运动学分析

周 伟，汪 阳，杨少锋，王兴海

（西安爱生技术集团公司，陕西 西安 710065）

引言

转子发动机由于运行噪音小、工作平稳、扭矩均匀、高转速性能好、功重比高等特点，在无人机航空领域有着广泛的应用[1-4]。

在转子发动机运转过程中，转子同前、后缸盖之间的密封主要通过安装在转子上的端面密封条（下文简称密封条）来实现[5]；研究转子发动机运行过程中密封条运动学特性，对转子发动机仿真分析[6-10]及新研转子发动机设计有较强的指导意义[11-14]。

1 模型建立

建模示意图见图1，由于三角转子发动机三个密封条为对称结构，仅对图中标记密封条（涂黑密封条）进行分析，为便于叙述，定义图中目标密封条正对的转子顶点为目标顶点。易知，DA 直线为目标密封条的对称轴。

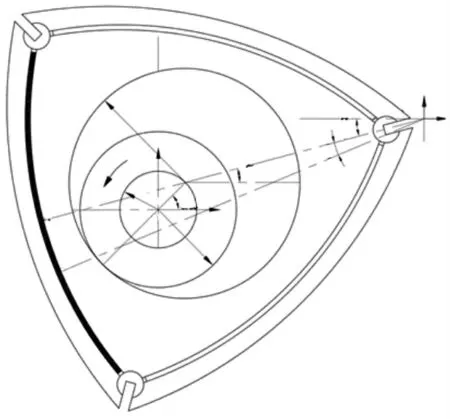
图1 建模示意图

图中各参数说明如下：A 点为目标密封条对称中心上的点；O 点为转子发动机旋转中心（主轴旋转中心）；C 点为三角转子旋转中心；D 点为端面密封条所在圆圆心；E 点为端面密封条上任意一点（目标点）所在位置（该点半径同密封条对称线夹角为θ）；L 为线段CD 距离，密封条圆心到三角转子旋转中心距离（密封条圆心位于转子中心到转子顶角的连线上）；R 为线段DE 距离，密封条上某点的半径值（本文为计算对比，所选点均位于密封条内侧边缘）；e 为发动机偏心距；α 为发动机主轴转动角度；ω 为发动机主轴运转角速度；θ 为端面密封条上任意一点所在位置同密封条对称轴夹角（-24°≤θ≤24°）。

根据转子行星齿轮运动关系及周转轮系原理易知，内齿轮节圆半径为3e，外齿轮节圆半径为2e；当发动机主轴旋转角度为α 时，三角转子旋转角度为α/3[15]。

2 详细计算

2.1 密封条上任意点轨迹计算

当密封条随转子在发动机中运动时，密封条上不同位置相对于静止的前、后缸盖的运动状态是影响转子发动机性能的重要因素。以图1 中O 点为几何中心，图中X 轴和Y 轴为参考系进行计算。当转子发动机主轴旋转α 后，三角转子中心C 点位置为式（1）和式（2）。

又因三角转子旋转角度为α/3，则目标径向刮片圆心D 位置为式（3）和式（4）。

以D 为参考坐标原点，易知DE 线同D 点正方向夹角为π+α/3+θ，则点E 位置为式（5）和式（6）。

简化后，密封条上任意一点轨迹方程为式（7）和式（8）：

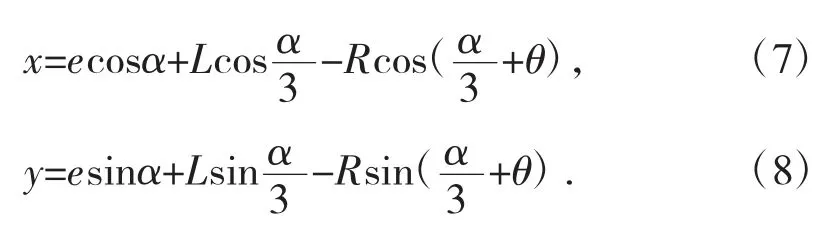
2.2 密封条上任意点速度计算

将密封条轨迹方程分别对时间进行求导，可分别获取目标点在X，Y 方向的分速度，见式（9）和式（10）：

式中ω 为偏心轴的角速度（rad/s），在转速不变的情况下为常数。

由于密封条上目标点速度方向恒与ω的方向相同，为方便起见，V 恒取正值，而不计目标点所在坐标的象限，速度计算如下式（11）：

2.3 密封条上任意点加速度计算

对速度分量继续关于时间求导，得出加速度分量如式（13）和式（14）：

为便于分析讨论，将绝对加速度进行转化，得出任一点沿端面密封条半径方向的法向加速度an为式（15），沿切线方向的at为式（16）：

计算并化简，得到法向加速度和切向加速度如式（17）和式（18）：

2.4 密封条内包络线计算

理论研究和实际观测结果表明，发动机旋转过程中，密封条上不同点的轨迹均为不同角向、不同尺寸的双弧长短幅外旋轮线，当目标点均位于密封条内侧时，上述外旋轮线族的内包络线即为冷却异型孔的最大名义尺寸。

求解密封条轨迹内包络线，对风冷型转子发动机缸盖冷却孔设计和误差分析有着重要的意义。

根据包络线理论进行计算，将式（7）、式（8）分别对α、θ 求偏导，化简如下式（19）至式（22）：

因sin2θ+cos2θ=1，带入式（24）进行计算。由于转子发动机为旋转结构，结合数据分析，在计算过程中均取正值带入计算，可获得所需内包络线如式（25）、式（26）。

将式（25）、式（26）带入式（7）、式（8），化简后得到包络线方程如式（27）、式（28）：

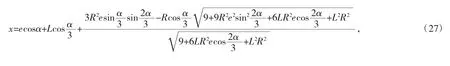
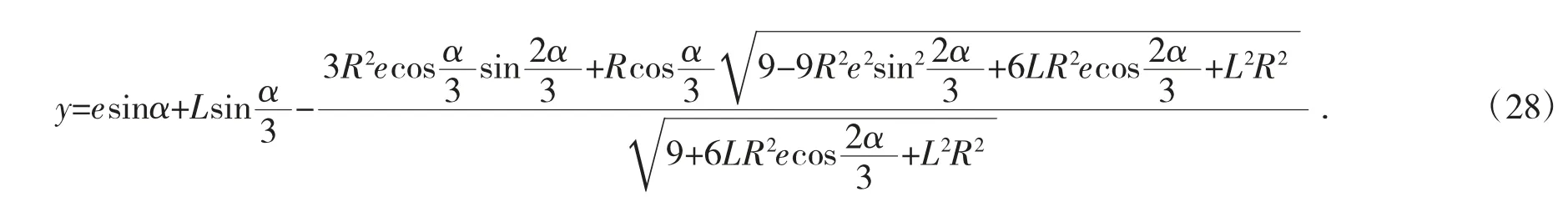
3 结果分析

为研究密封条运行工况，沿密封条中心线DCA向两侧分别间隔8°取点进行分析，结果如下。易知图中示意点-24°、24°，-16°、16°，-8°、8°分别关于密封条中心线DA 呈对称分布，图中0°点为密封条中心点，即为图1 中点A（上述角度值即为图1 中θ 值）。

根据现有航空转子发动机研究情况，图1 中相关计算参数取值如下：L 为74.5 mm；R 为118.5 mm；e 为11.6 mm；α 为0°～1 080°；ω 为628.32 rad/s，对应主轴转速6 000 r/min。

转子旋转一圈，发动机主轴旋转三圈。当α 取0°、540°、1 080°时，目标顶点位于缸体长轴位置，目标密封条对应燃烧室体积最大；当α 取270°、810°时，目标顶点位于缸体短轴位置，目标密封条对应燃烧室体积最小。

3.1 密封条运动速度分析

发动机密封条上某点运行速度同主轴转角的关系见图，速度在0°～540°、540°～1 080°范围呈周期性变化。

目标点同密封条对称中心夹角越大，对应的最大速度越高，但无论位于何种位置，该点运行速度极限差值相同。

当α 取0°、540°、1 080°时，目标顶点位于缸体长轴位置，目标密封条中心点A 速度最小；当α取270°、810°时，目标顶点位于缸体短轴位置，目标密封条中心点A 速度最大。各目标点速度曲线分别关于α 等于0°、270°、540°、810°、1 080°等呈轴对称分布。

密封条速度变化图如图2 所示。

图2 密封条速度变化图

3.2 密封条法向加速度分析

发动机密封条上某点运行法向加速度同主轴转角的关系见图3，法向加速度在0°～540°，540°～1 080°范围呈周期性变化。目标点同密封条对称中心夹角越大，对应的最大法向加速度越高，但无论位于何种位置，该点运行法向加速度极限差值相同。

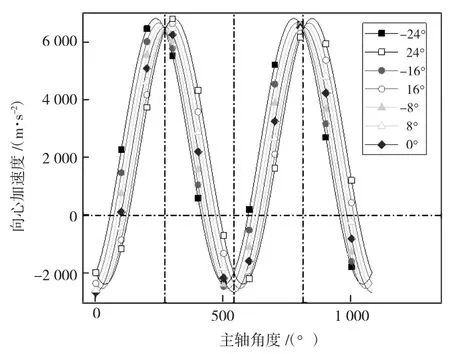
图3 密封条法向加速度变化图

当α 取0°、540°、1 080°时，目标顶点位于缸体长轴位置，目标密封条中心点A 法向加速度最小；当α 取270°、810°时，目标顶点位于缸体短轴位置，目标密封条中心点A 法向加速度最大。各目标点法向加速度曲线分别关于α=0°、270°、540°、810°、1 080°等呈轴对称分布。

3.3 密封条切向加速度分析

发动机密封条上目标点切向加速度同主轴转角的关系见图4，切向加速度在0°～540°，540°～1 080°范围呈周期性变化。同速度和法向加速度分布不同，数值不再呈轴对称分布。不同位置点切向加速度极限差值也不同，但对称点极限差值相同。最大切向加速度位于24°目标点，最小切向加速度位于-24°目标点，最大值最小值幅值相同。

图4 密封条切向加速度变化图

当切向加速度为正值时，呈加速状态，当切向加速度为负值时，呈减速状态。以密封条中心点A 数据为参考进行分析，在α 为0°～270°时，A 点呈先减速后加速状态，其中0°和270°时，at值均为0；在α 为270°～540°时，A 点也呈先减速后加速状态，其中270°和540°时，at值均为0。在单个循环周期内，切向加速度在50.0%的主轴转角区域为正值，呈加速状态；在50.0%的主轴转角区域为负值，呈减速状态。

3.4 上、下止点运动密封条运动状态分析

根据转子发动机运行原理可知，不区分进排气和点火区间时，当α 等于0°或540°时（1 080°即为0°位置），目标顶角位于气缸型面长轴处，图示密封条位于名义下止点（BDC）位置；当α 等于270°或810°时，目标顶角位于气缸型面短轴处，图示密封条位于名义上止点（TDC）位置。本文重点对目标顶点位于0°及270°时密封条的运行参数进行分析。

图5 分别为α 等于0°、270°时密封条不同位置的速度分布图，无论密封条位于上止点还是下止点，密封条速度均关于密封条中心呈对称分布，同对称中心夹角越大，速度值越高。

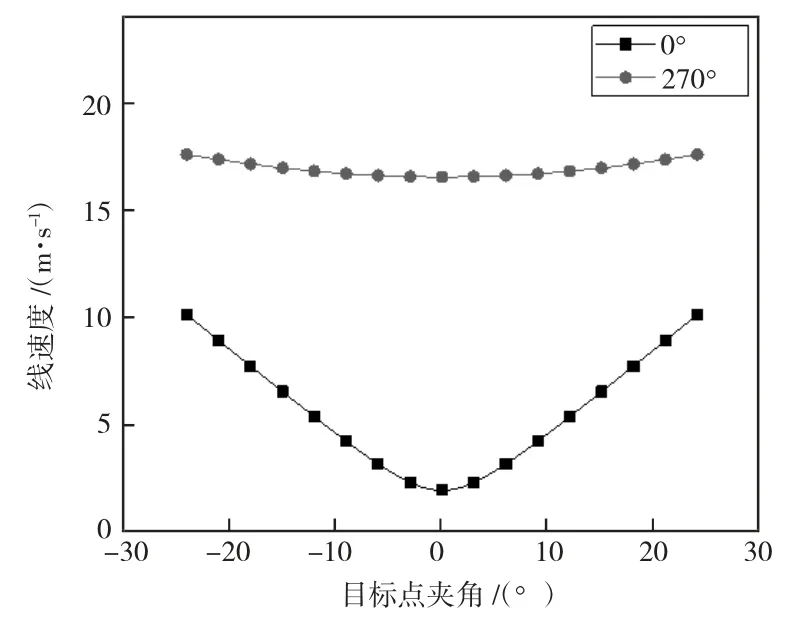
图5 密封条速度分布图

0°时密封条总体速度较小，但两端同对称中心差值较大，最高速度约为对称中心的526.1%；270°时密封条总体速度较大，但两端同对称中心差值较小，最高速度约为对称中心的106.4%。

无论密封条位于上止点或下止点，密封条法向加速度均关于密封条中心呈轴对称分布，如图6 所示，同对称中心夹角越大，法向加速度幅值越低。0°时密封条总体法向加速度较小，且为负值，方向背离圆心方向，两端法向加速度同对称中心差值绝对值较大，末端法向加速度约为对称中心的74.4%。270°时密封条总体法向加速度较大，且为正值，方向朝向圆心方向，但两端法向加速度同对称中心差值绝对值较小，末端法向加速度约为对称中心的98.3%。

图6 密封条加速度分布图

切向加速度关于对称中心呈中心对称分布，夹角越大，切向加速度幅值越大，对称中心切向加速度值均为0。0°时，对称中心前段切向加速度为负值，呈现减速状态，对称中心后段切向加速度为正值，呈现加速状态；270°时，对称中心前段切向加速度为正值，呈现加速状态，对称中心后段切向加速度为负值，呈现减速状态。270°时切向加速度幅值较大，末端加速度约为0°时末端加速度的655.7%。

3.5 密封条包络线分析

分别计算包络线示意图如图7 所示，图中有效段为最终节选的包络线，即异型孔最大理论尺寸。

其中，有效段角度对应关系为：0°≤α≤116°；424°≤α≤656°；964°≤α≤1 080°。

从图7 中可见，包络线过渡光滑，同密封条轨迹不同点内侧极限位置相切，完全满足转子冷却孔设计要求。

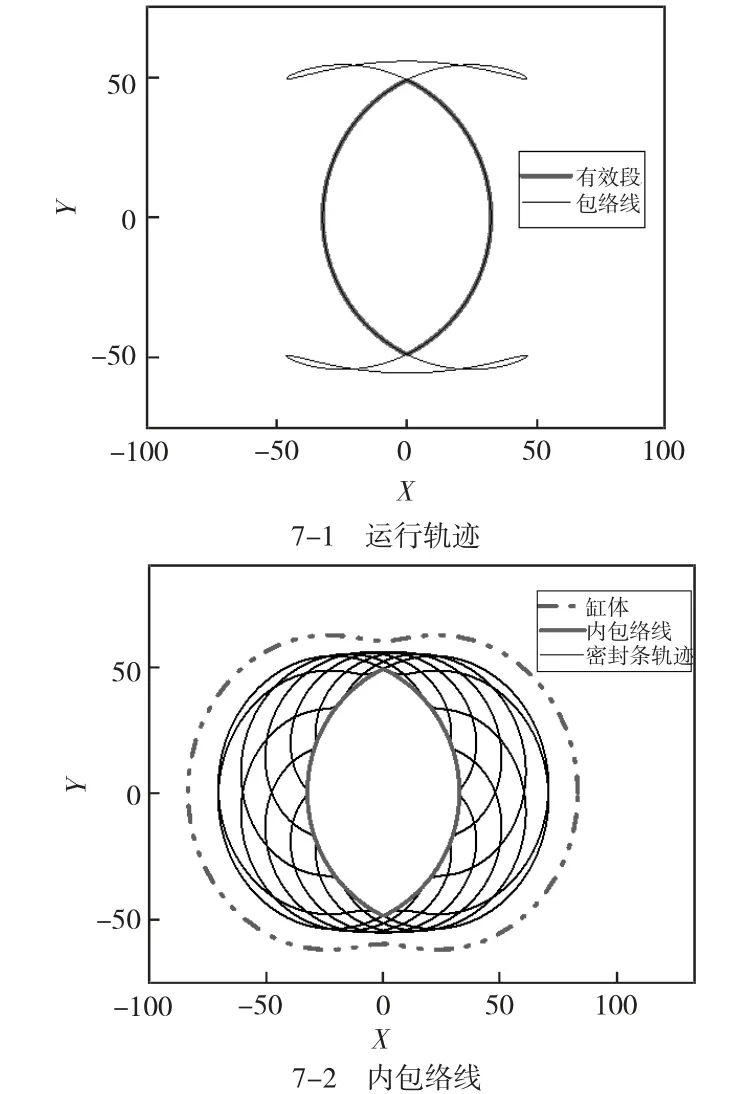
图7 密封条运行轨迹及内包络线示意图

4 结论

本文针对转子发动机端面密封条为研究对象，研究了密封条运行轨迹、速度、加速度变化规律，得出以下结论：

1）发动机运行过程中，速度、法向加速度关于密封条中心呈对称分布，且极限差值相同，速度曲线，法向加速度曲线分别关于α 为0°、270°、540°、810°、1 080°等呈轴对称分布；

2）切向加速度在周期内呈两次先减速、后加速状态，加减速各占50%的主轴转角；

3）在上止点、下止点位置时，速度、法向加速度关于密封条中心呈轴对称，切向加速度关于密封条中心呈中心对称；

4）求取包络线过渡光滑，同密封条实际运行轨迹完美相切，能满足冷却孔设计要求。