基于等效单层理论的钢-混组合梁动力分析方法

孙琪凯， 张 楠， 张 冰， 刘 潇， 程泽农， 陶晓燕

(1.北京交通大学 土木建筑工程学院，北京 100044；2.中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081；3.高速铁路轨道技术国家重点实验室，北京 100081；4.中铁工程设计咨询集团有限公司 城市轨道交通设计研究院，北京 100055)

钢-混组合梁是指由混凝土板和钢梁两部分组成并采用柔性剪力键传递结合面之间剪力的一种新型结构形式。这种结构既能够发挥钢材抗拉又能够发挥混凝土抗压的材料特点。因其具有自重轻、承载力高等特点，而在工程中被广泛应用，特别是高速铁路桥梁中。由于抗剪连接件是柔性的，即使很小的荷载作用下，混凝土梁和钢梁之间也会产生相对滑移[1-2]，使组合梁动力分析时必须考虑滑移带来的影响。钢-混组合梁动力特性分析是为了研究结构振动的固有规律，是研究其相关动力性能的基础，可以为下一步分析钢-混组合梁动力荷载响应做准备。目前，已有学者开始关注钢-混组合梁动力特性的分析。

Newmark等[3]是最早基于Euler-Bernoulli梁理论分析组合梁受力性能的研究学者之一，在试验分析的基础上，Newmark等提出并验证了子梁界面间存在相对剪切滑移，并且滑移量与剪切力有关。随后，大量的学者扩展了这一理论。Girhammar等[4]采用直接平衡法推导了考虑界面上剪切滑移的钢-混组合梁的运动平衡微分方程，得到了自振频率解析解。后又进一步推导了一般弹性支撑时，钢-混组合梁动力特性解析解[5]。Huang等[6]讨论了边界条件为简支-简支、固支-自由、固支-简支和固支-固支的情况下，钢-混组合梁自振特性随剪力连接键刚度的变化规律以及移动荷载作用下组合梁的动力响应。侯忠明等[7]根据理论分析结果，提出了钢-混组合梁的频率折减系数和刚度折减系数。杨骁等[8]研究了界面掀起和轴向力双重作用对钢-混组合梁动力弯曲特性的影响。以上这些研究均没有考虑横向剪切变形的影响。然而，对于大高跨比、低抗剪刚度或连续跨度的组合梁，横向剪切变形的影响是不容忽视的。因此，将Timoshenko梁理论应用于组合梁的研究。

在Timoshenko梁理论中，假定各子层在弯曲前垂直于其轴线的横截面一直保持平面，但是变形后不再垂直于子层轴线。Xu等[9-12]基于Timoshenko梁理论研究了组合梁的虚功原理和功互等定理，分析了材料和几何参数变化、剪力连接键刚度等因素对组合梁动力性能的影响。李晓伟等[13]提出了求积元法，提高了有限元法在组合梁动力特性与瞬态响应分析中的计算效率。然而，组合梁截面上剪切应力的实际变化是抛物线形的，在梁顶和梁底表面应为零。因此，基于Timoshenko梁理论很难准确预测组合梁的应力分布。此外，它也不能得到令人满意地精确的组合梁动力响应。为了解决这些问题，人们开始用高阶梁理论来描述组合梁的位移场。常用的高阶梁理论有Reddy梁理论[14]和Kant梁理论[15-16]，He等[17-19]把Kant梁理论用于组合梁研究。与Kant梁理论相比，Reddy梁理论保留的未知项更加精炼，使其在应用中更加有优势[20-21]。

对于钢-混组合梁剪力滞效应对结构动力性能影响的研究已比较常见。周旺保等[22]分析了相对滑移和剪力滞效应对连续钢-混组合箱梁自振特性的影响，结果表明：当自振频率低阶时，剪力滞效应的影响很小。陈玉骥等[23]分析了相对滑移和剪力滞效应对钢-混组合梁一阶自振频率的影响，得出了剪力滞效应对自振频率的影响很小，可略去不计的结论。综上所述，剪力滞效应对钢-混组合梁一阶自振频率的影响可忽略不计。

苏庆田[24-27]对钢梁和混凝土板界面连接处的黏结效应和摩擦效应进行了试验和理论研究，结果表明：黏结效应和摩擦效应对钢-混组合梁的动力性能影响较小，一般可忽略不计而只考虑二者间的剪力连接键作用。

本文基于Reddy高阶梁理论和黏结滑移理论，提出了钢-混组合梁动力的等效单层理论有限元计算模型。使用Heaviside函数构造双层组合梁的轴向变形的高阶理论位移场，使其预先满足子梁间的剪力连续、位移和应变不连续和上下自由表面条件。从而，得到不包含横向位移一阶导数∂W/∂x的等效单层位移场函数，因此在有限元计算时只需构造C0连续插值函数，提高了计算效率。最后，通过与已发表文章中数值模型结果对比，验证了文中有限元计算模型的适用性，讨论了高跨比对文中理论计算精度的影响。

1 等效单层理论位移场

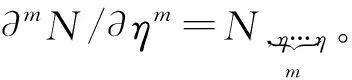
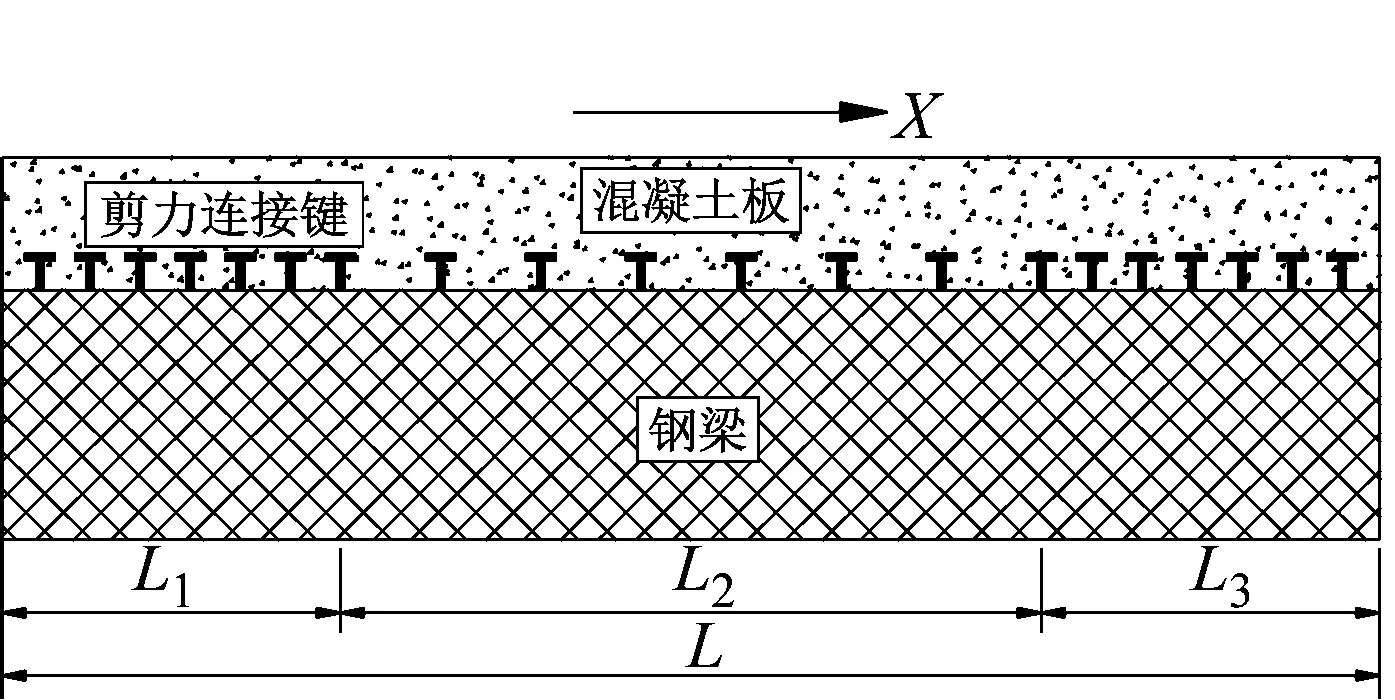
图1 钢-混组合梁构造图Fig.1 Structure of steel-concrete composite beam

基于Reddy高阶梁理论和和黏结滑移理论，将双层钢-混组合梁等效为单层梁结构。基本假定如下：(1) 混凝土板与钢梁之间始终保持竖向密贴而水平向可相对滑动；(2) 钢-混组合梁沿厚度方向的正应变和平面外剪切应变均可忽略不计；(3) 钢-混组合梁满足小变形假设；(4) 混凝土板与钢梁之间是光滑的,结合面处剪力全部由剪力连接键承受，剪力键等效为连续分布的弹簧，弹簧水平刚度为常量K。

基于Reddy高阶梁理论的位移场如图2所示，建立笛卡尔坐标系，满足h1=h2+h3=h/2，h为组合梁高。

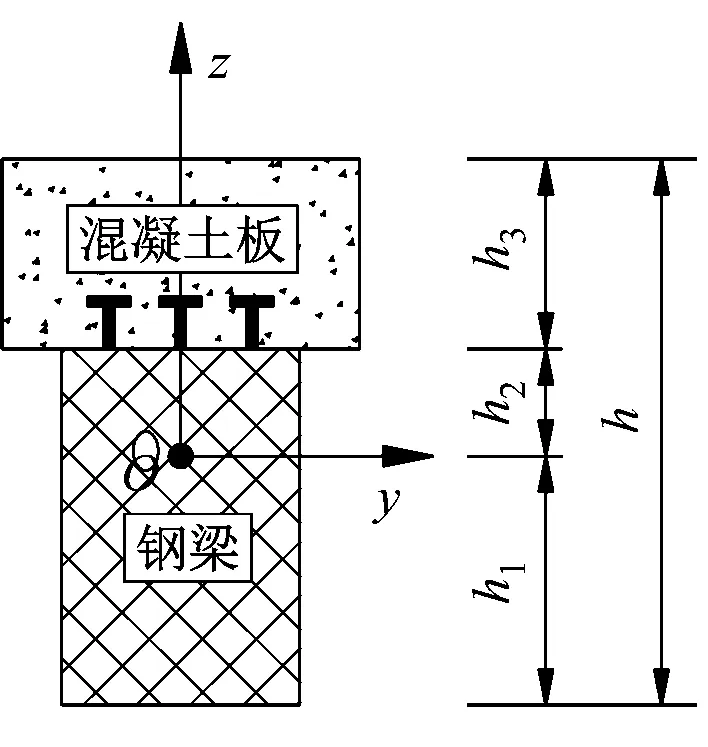
图2 钢-混组合梁位移场构造图Fig.2 Displacement field of steel-concrete composite beam

使用Heaviside函数构造基于Reddy高阶剪切理论的双层钢-混组合梁位移场函数。该函数在钢-混凝土结合面上满足位移协调和应力平衡条件。结合面处，钢梁和混凝土板表面的剪力相等，但由于结合面处两个子梁的面积不同且两种材料的弹性模量不同，故其剪应力和剪应变不相等，这表示钢-混组合梁位移场函数在结合面处的一阶导数不连续。根据位移场函数的这一特征，假设组合梁等效单层理论位移场函数如下

(1)

式中:U、W分别为钢-混组合梁的轴向位移和横向位移；H(x)为Heaviside函数；ui(i=0～3)为假定单一截面时轴向位移沿梁高的分布函数；δi(i=0～3)为由于材料不同和剪力连接键柔性造成得混凝土板层轴向位移分布函数的变化量。

本文基于线弹性假设，因此钢-混组合梁的应力、应变和剪力连接键刚度满足如下关系：

(1) 钢-混组合梁轴向应变和剪切应变如下

(2)

(2) 应力-应变关系为

(3)

式中:σxx、τxz分别为正应力和剪应力；εxx、γxz分别为正应变和剪应变；E、G分别为弹性模量和剪切模量；Qcs、K和Ucs分别为组合梁单位长度的剪力连接键的合计剪力、剪切刚度和剪切滑移量。

首先，使假设的位移场函数式(1)满足顶、底板自由表面条件，有以下公式成立

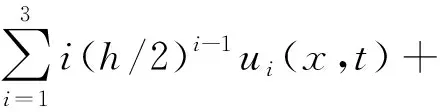
(4)

(5)

由式(4)、式(5)，可把u2和δ2表示出来，如下

(6)

式中，α0=1/h,α1=3h/4,β0=-2/h,β1=-3h/2,β2=-1/h,β3=-3h/4。

然后，使假设的位移场函数式(1)满足层间剪力连续条件，有以下公式成立

(7)

式中:Qc、Qs分别为混凝土板底面和钢梁顶面的剪力；Gc、Gs分别为混凝土板和钢梁的剪切模量；γxz,c(h2)、γxz,s(h2)分别为混凝土板底面和钢梁顶面的剪切应变；Ac、As分别为混凝土板底面和钢梁顶面的面积。

再者，由钢-混结合面上的剪力与剪力连接键承受的剪力相等可得

(8)

由式(7)、式(8)，可表示出u3和w0,x，如下

(9)

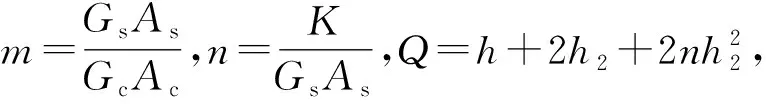
将式(6)和式(9)代入式(1)可得钢-混组合梁的等效单层理论位移场函数

(10)

式中，Ψ0(z)=H(z-h2)[1+(C0β0+D0β1)z2]+

(C0α0+D0α1)z2+D0z3，

Ψ1(z)=H(z-h2)[z+(C1β0+D1β1+β2)z2]+

(C1α0+D1α1)z2+D1z3，

Ψ2(z)=H(z-h2)[z3+(C2β0+D2β1+β3)z2]+

(C2α0+D2α1)z2+D2z3。

式(10)即为等效单层位移场函数。其不包含横向位移一阶导数∂W/∂x，因此在有限元计算时只需构造C0连续插值函数。对应于式(10)的自由(F)、简支(S)和固支(C)等三种工程中常见的边界条件为

(11)

2 运动微分方程及求解

根据虚功原理，基于式(10)的钢-混组合梁的动力响应可以表示为

(12)

式中:σxx、τxz、εxx和γxz分别为组合梁的正应力、剪应力、正应变和剪应变；q(x,t)为作用在组合梁上的横向力。

如式(13)所示，采用一维有限元近似分析钢-混组合梁动力特性时，将u0、u1、δ0、δ1、δ3和w0作为位移场的相关分量。构造一个3节点的C0连续等参梁单元，三个节点记作1，2，3，以节点2为原点。根据等参公式[28]，所有变量都是根据其节点值进行插值的，其表达方式为

v=Nδe

(13)

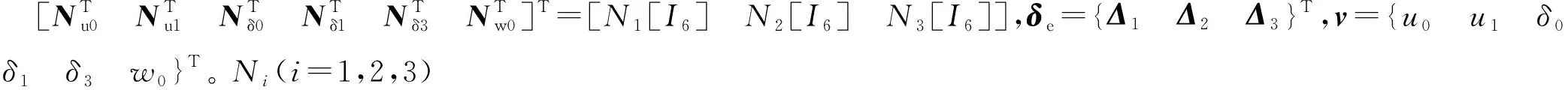
根据上述公式，可导出式(13)中所需的所有形状函数向量。对于轴向和横向位移，形状函数矢量可以写成

(14)

正应变和剪应变的形状函数为

(15)

分界面处剪切滑移量的形状函数为

(16)

把式(14)、式(15)和式(16)代入式(12)可得

(17)

由于(δδe)T是任意的，在满足位移边界条件的前提下，式(17)可以简化为标准的有限元离散方程

(18)

式中，Me、Ke和Fe分别为单元质量矩阵、单元刚度矩阵和单元力向量。如下

(19)

因此，钢-混组合梁的自由振动的公式为

(Kg-ω2Mg){Φ}=0

(20)

式中:Mg和Kg分别为整体质量矩阵和整体刚度矩阵；{Φ}为整体振幅向量；ω为自振频率。

3 算例分析

He等分别基于Euler-Bernoulli梁理论(EBT)和Timoshenko梁理论(TBT)，给出了简支-简支(S-S)、固支-简支(C-S)、固支-自由(C-F)和固支-固支(C-C)等四种边界条件(图3)下，不同高跨比的钢-混组合梁自振频率计算结果。本节的目的是通过与He等的计算结果进行对比，验证文中有限元计算模型可适用于常见的四种边界条件，并讨论该理论的计算精度。

He等的分析模型的梁长由高跨比确定，各层截面和材料特性见图4。剪力连接键刚度为K=50 MPa。ANSYS建模时，上下层结构均采用采用SOLID65单元，单元数为5 760个，节点数为9 660个。采用COMBIN39三维弹簧单元连接上下两层结构，竖向耦合，纵横向为弹性约束，弹簧刚度取值为剪力键刚度。根据本文的式(17)～式(20)采用Matlab编制有限元计算程序，计算该算例的一阶竖向自振频率。四种边界条件下，高跨比分别为0.05、0.2和0.5时，本文计算模型、He等计算模型和ANSYS FEA计算模型(见图5)的一阶自振频率计算结果见表2。括号内数值为计算值与ANSYS FEA计算值的误差，(f数值-fANSYS)/f数值×100%。

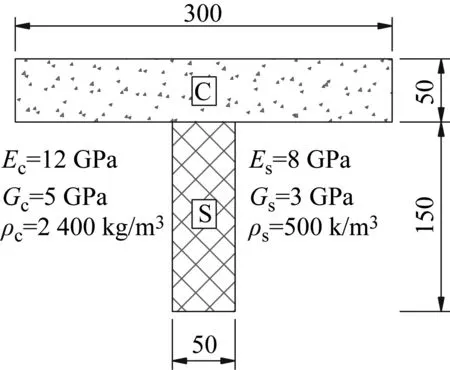
图4 组合梁的尺寸和材料特性Fig.4 Dimensions and material properties

(a) 高跨比为0.5

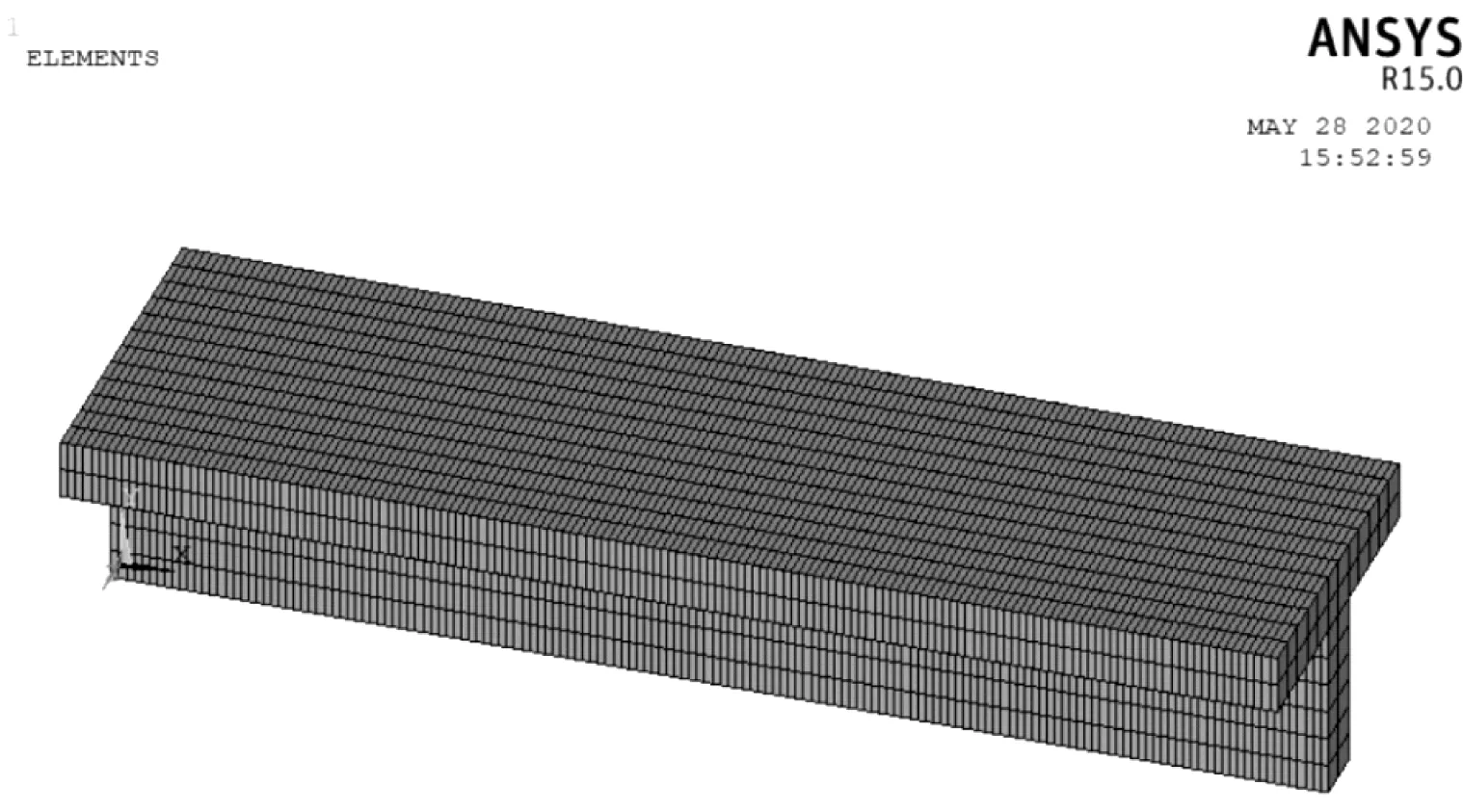
(b) 高跨比为0.2

(c) 高跨比为0.05图5 ANSYS FEA计算模型Fig.5 The calculation model of ANSYS FEA

三种高跨比下，采用上述四种方法计算所得的边界条件为简支-简支的振型结果见图6。

表2和图6结果表明：

(1) 四种边界条件各种高跨比下，本文提出的有限元计算模型的基频计算结果与ANSYS FEA计算结果基本一致。说明了四种常见边界条件下，等效单层理论有限元计算模型均可适用于分析钢-混组合梁的自振特性。

(2) 本文基于Reddy高阶梁理论提出的计算模型的计算精度明显高于Euler-Bernoulli梁理论和Timoshenko梁理论计算模型，而且高跨比越大，该计算模型的准确度优势越明显。

(3) 本文模型、ANSYS FEA、Euler-Bernoulli梁理论和Timoshenko梁理论分析得到的结构振型模态基本一致。

4 结 论

通过以上分析，结论如下：

(1) 基于Reddy高阶梁理论和黏结滑移理论，提出了钢-混组合梁动力分析的等效单层理论有限元计算模型。模型中预先满足层间剪力连续和上下自由表面条件，使得等效单层位移场中不包含横向位移一阶导数∂W/∂x，有限元计算时仅需构造C0连续插值函数。

(2) 通过与已发表的文章中算例结果对比，说明了文中提出的等效单层理论计算模型可适用于四种常见的边界条件和任意高跨比的钢-混组合梁动力特性的分析。

(3) 三种典型高跨比下，本文模型、ANSYS FEA、Euler-Bernoulli梁理论和Timoshenko梁理论分析得到的结构振型模态基本一致。

(4) 本文提出的计算模型具有较高的计算准确度，且与Euler-Bernoulli梁理论和Timoshenko梁理论计算模型相比，高跨比越大，等效单层理论有限元计算模型的准确度优势越明显。

表1 不同计算方法的竖向一阶自振频率对比表Tab.1 Comparison of vertical fundamental frequencies