外激与参激作用下非光滑形状记忆合金梁的概率响应
李玉婷, 冯进钤, 岳晓乐
(1.西安工程大学 理学院,西安 710048;2.西北工业大学 数学与统计学院,西安 710072)
在实际工程中,由于碰撞是一种无法避免的非光滑因素,故其响应问题是非线性动力学中的热点课题之一。Xu等[1-2]将Hertz接触模型进行改进,并运用等效非线性方法推导得出碰撞振动系统的响应;李超[3]通过广义胞映射方法得到该系统的响应结果;Rong等[4]应用多尺度方法,谐和与噪声双重干扰之下系统的平均响应被预测得到;Zhu等[5-10]将指数多项式闭合方法运用到随机激励下碰撞振动系统的研究中,得到了许多新颖的结果。
在众多研究方法中,随机平均法是一种研究随机振动系统的有效方法。近年来,该方法的应用越来越广泛。例如聂旭涛等[11]构建了随机因素作用下伺服机构的动力学模型,并由随机平均法和点插值无网格推导,得到了模型的响应;张波等[12]在非线性悬挂轮系统中加入了高斯白噪声参激,通过Hamilton系统平均法分析了随机全局稳定性以及分岔现象;针对非弹性碰撞系统,徐明等[13]研究了噪声作用下系统的首次穿越问题;对于噪声作用下五自由度强非线性随机振动系统,张雷等[14]利用基于广义谐和函数的随机平均法,得到了系统的平均首次穿越时间、条件可靠性函数以及平均首次穿越时间的条件概率密度。针对碰撞振动系统,Dimentberg等[15]利用广义随机平均法讨论了碰撞振动系统的响应问题。对于双参激作用下Van der Pol模型的随机响应,Yang等[16]应用随机平均法给出了结论。Feng等[17-18]分析了噪声激励下Duffing振子的响应及分岔问题。针对多自由度碰撞振动系统,Huang等[19]通过随机平均法对其响应进行了研究。从平均能量损失角度出发,Gu等[20]则提出了一种分析碰撞振动系统的平均方法,并通过实例说明该方法是可行的。基于雅可比椭圆函数的随机平均法,郑丽文等[21-23]预测了有界噪声和白噪声作用下系统的响应。在非线性动力学中,噪声的扰动会使系统产生随机共振现象,包括外激振动和参激振动。外激振动会使系统状态有一定程度的扩散;而在参激系统中,任意小的干扰都有可能导致运动状态发生质的变化。因此,研究外激与参激联合作用下的随机振动具有重要意义。
形状记忆合金(shape memory alloy, SMA)是一种新型智能材料,具有十分特殊的性能:形状记忆效应。形状记忆效应指的是合金在加热升温后会迅速恢复为低温状态下的形状,是热弹性马氏体相变的宏观体现。该材料被广泛应用在许多领域,例如生物医疗领域,形状记忆合金可被制成患者所需的生物支架,术前低温状态下将其折叠为最小体积,在送入人体之后,经过温度处理,使其展开形成支架,这样可以大大地减小手术创伤和患者的病痛。随机分岔是系统全局性态发生突变的一种现象,它的产生说明随机激励使得系统解的性质发生了突变[24-28],往往对系统的整体稳定安全结构起着关键作用。然而,关于SMA响应和分岔的研究相对较少,所以本文主要研究了具有非光滑特征、外激与参激联合作用下SMA梁的概率响应和分岔。第2章建立外激和参激联合作用下SMA梁模型。第3章利用非光滑变换,应用随机平均法得到的平均Fokker-Planck-Kolmogorov (FPK)方程,进而得到稳态解析结果。第4章通过Monte Carlo法验证了结果的有效性。此外,利用解析结果的极值条件得到了系统的随机分岔临界条件,着重研究了阻尼力与碰撞恢复力对系统响应的影响。
1 形状记忆合金梁模型
如图1所示,考虑一个矩形SMA梁模型[29]。梁长为l,宽为b,厚度为h,并且受随机激励
F1=s0+s1ζ1(t),F2=s0+s2ζ2(t)
(1)
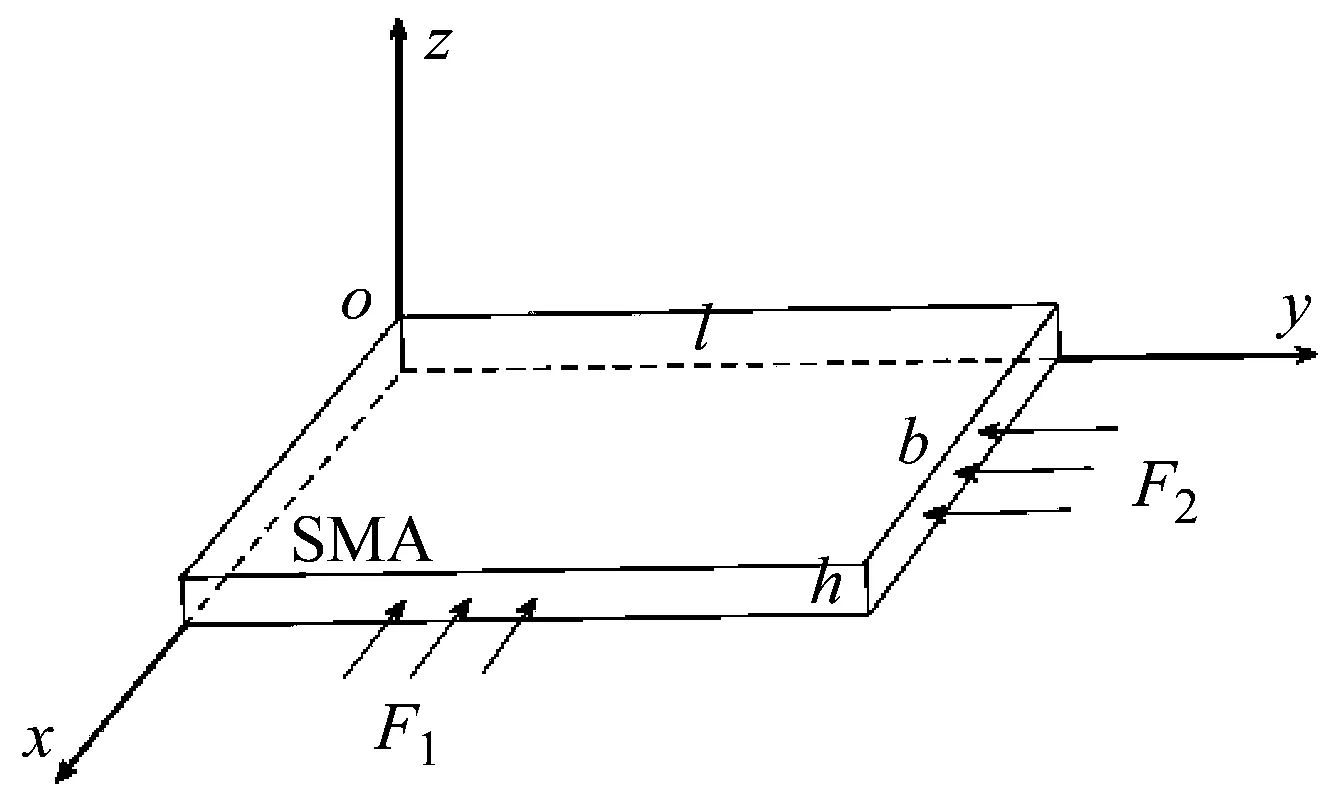
图1 SMA梁模型Fig.1 The model of SMA beam
式中:s1和s2为位移,s0为初始时刻的位移;ζ1(t),ζ2(t)为相互独立的标准高斯白噪声。ζ1(t)和ζ2(t)满足
E[ζ1(t)]=0,E[ζ1(t+τ)ζ1(t)]=δ(τ)
E[ζ2(t)]=0,E[ζ2(t+τ)ζ2(t)]=δ(τ)
梁的边界条件的一阶模态为
(2)
结合式(1),并利用梁的边界条件、几何变性条件,由弯矩公式可得
(3)
其中
式中:mi(i=1,2,3,4)为迟滞环骨架曲线与实验曲线的偏差;η是梁的几何变形条件。
该梁的动力学方程为
(4)
式中:M是梁的弯矩;c是线性阻尼;ω是梁竖直方向上的位移;ρA表示单位长度梁的质量。
将式(1)、式(2)和式(3)代入式(4)并进行积分,无量纲化后可得随机激励下形状记忆合金梁的运动方程
(5)
式中
在葛根等的SMA梁模型的基础上,本文考虑非光滑因素碰撞对梁的影响,得到了外激和参激联合作用下的形状记忆合金梁振动模型如下
(6)
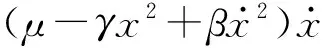
2 概率响应
由于非光滑因素的存在使得系统不易直接研究,故利用非光滑变换[30],得到系统(6)的近似等效系统
3.1 经济效益分析 按照当前水稻种植的水平,生产投入7 575元/hm2,田租7 500元/hm2,水稻产量在8 250 kg/hm2左右,利润在6375元/hm2左右。通过虾稻鳜综合种养,由于虾、鳜养殖分摊了田租和人工成本,且减少了农药、肥料的使用,水稻种植成本仅7 375元/hm2,成本下降了51.1%;在产量仅6 250 kg/hm2的情况下,利润达到8 875元/hm2。
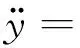
f1sgn(y)ζ1(t)+f2yζ2(t)
(7)

(8)
由Khassminskii定理[31]知,引入小参数ε>0,当ε→0时,H被近似为一个Markov过程,则平均It微分方程为

(9)
式中

(10)
(11)
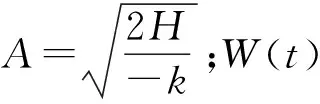
平均后的FPK方程为
(12)
其稳态解
(13)
式中
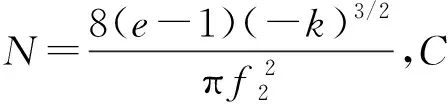
(14)
最终,位移x1和速度x2的PDF为
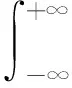
(15)

(16)
3 概率响应分析
3.1 数值仿真
在本小节中,利用Monte Carlo法,对原系统(6)进行数值仿真得到数值结果,证明解析结果(13)的正确性,从而验证该随机平均法的有效性。另外,讨论不同的噪声幅值f1,f2对系统响应的影响。参数固定为k=-1,μ=0.01,γ=0.01,β=0.01,e=0.98。
图2表示不同噪声幅值激励对系统响应的影响,图3表示加性噪声幅值f1=0.2时系统的联合概率密度函数。由图可知解析结果和数值结果拟合的很好,验证了该随机平均法的有效性。由图2(a)、(b)和(c)知,随着噪声幅值的增大,能量、位移和速度的概率密度函数曲线峰值越低,这表明噪声的扰动使得系统逐渐偏离平衡状态。
3.2 随机分岔
本节固定系统参数k=-1,γ=0.01,β=0.01,f1=0.1,f2=0.1,由解析结果可得系统产生随机分岔的临界线,进而得到阻尼系数μ和恢复力系数e使得系统发生分岔的临界值。
由解析结果(13)的极值条件得到系统发生分岔的临界条件为
(17)
图4中实线为随机分岔临界线,可以看到随机分岔临界线将区域一分为二,左上部分为火山口区域,也就是当对应参数为该区域的值时,系统响应峰的形状呈现“火山口”,即会发生分岔现象;而右下部分是单峰区域,对应的峰的形状为单峰,即系统此时未发生分岔。在临界线附近取三点A(-0.01,0.99)、B(-0.01,0.98)和C(-0.03,0.98),由上述分析可得,当系统取点A或点C时,系统发生分岔;而当取点B时未发生分岔。

图4 的随机分岔临界线Fig.4 The critical line of stochastic bifurcation
为进一步验证随机分岔临界线的有效性,图5(a)、(b)和(c)分别表示点A、B和C的联合PDF曲面图,可以清楚地看到图5(a)曲面发生凹陷,并呈现火山口形状,图5(b)曲面则是单峰,而图5(c)曲面出现明显的火山口形状。经过分析发现,对比点A和点B,固定μ=-0.01,较大的e值更易使得系统产生分岔;而结合点B和点C比较得出,同一恢复力系数e=0.98下,系统取较小的μ值时容易发生分岔。
图6表示不同线性阻尼μ下系统的联合PDF。固定碰撞恢复力系数e=0.98,随着阻尼系数不断减小,PDF曲线的峰值在不断降低。当μ=-0.013时,峰值趋于平滑状态,直到μ=-0.02时出现清晰的火山口。由此可得,阻尼系数μ诱导系统发生分岔的临界值为μ≈-0.013。
图7表示不同恢复力e下系统的联合PDF。图7与图6具有相似的变化历程,固定线性阻尼μ=-0.01,当恢复力系数e逐渐增大时,PDF曲线峰值在不断地趋于平滑,当e=0.984时,该峰形状平缓并伴随下凹趋势,直到在e=1.0形成火山口形状。由此表明,当碰撞恢复力系数增大时,系统的能量损失越大,而恢复力系数使得系统产生分岔值为e≈0.984。
4 结 论
本文应用随机平均法,主要研究了非光滑SMA梁在外激和参激噪声联合作用下的概率响应及其分岔。首先由非光滑变换得到近似等效系统,通过随机平均法和It公式推导得到系统的PDF并验证。研究结果表明,随机扰动会使得系统不断偏离平衡状态。进一步分析发现,阻尼力和碰撞恢复力可诱导系统发生分岔现象,由近似解析结果得到了系统产生分岔的临界条件,并验证了该条件的正确性。分岔破坏SMA梁的稳定性,易构成不安全隐患。本文分岔临界条件的产生使得研究系统分岔有了更加直观具体的方法,有助于通过调整系统参数来抑制随机分岔的发生,使得工程构建更加安全可靠。

