埋地管线下方土体流失对管线受力变形的影响研究

梁渭溪 雍睿 李朝旺

摘要： 埋地管线长期使用中会发生渗漏、管周土体不均匀沉降等问题，使得管线受力平衡状态被打破，在土体自重荷载和地表荷载的共同作用下容易引起邻近管线的破坏。为了分析管线的受力和变形，采用角点法和Winkler弹性地基梁理论，构建管-土耦合模型，推导出管线的受力变形方程。基于ABAQUS有限元软件模拟管-土耦合模型，对比分析数值模拟和理论计算的结果，以验证管线受力变形方程的有效性。结果表明：① 基于Winkler弹性地基梁理论的管- 土耦合作用模型可以求得有效的管线受力变形方程，其理论解与数值模拟解相差仅为3.31%～3.43%。② 在地表荷载作用下，沿远离土体流失区中心方向，位移逐渐变小，剪力逐渐增大，且在土体流失区边缘附近达到峰值后慢慢减小，出现反弯剪力最后趋于零，而弯矩逐渐增大达到峰值后慢慢减小。③ 当无地表荷载作用时，管线的受力变形比有地表荷载作用时小17.32%～20.77%。所提出的管线受力变形方程能够正确反映上覆荷载作用下管线受力的基本特征，可为工程中管线受力变化控制提供参考依据。

关 键 词： 埋地管线; 受力变形; 管-土耦合模型; 角点法; Winkler弹性地基梁理论

中图法分类号：  TU16

文献标志码：  A

DOI： 10.16232/j.cnki.1001-4179.2021.08.028

0 引 言

埋地管线作为天然气、石油、自来水等资源的运输工具，具有运输快速、便捷、不占地面空间等优点，它是城市供水、供气、热力供给、排污等地下生命线系统的基本组成部分[1-2]。管线因施工方式不恰当、材料老化、养护不到位、管壁腐蚀等问题，容易引起管线的渗漏。其次，管线周围的土体发生不均匀沉降或者邻近位置的管线破裂以及地下水的过度开采，都会导致管线周围土体流失，力学特征发生改变。另外，由于降水、人类活动等原因也会引起管线的上覆荷载发生变化，改变管线原有的受力平衡。

国内外学者采用不同的方法对埋地管线的力学特征展开研究。理论研究方面，Vorster等[3]考慮了隧道施工、土体非线性受力变形特性等因素对既有管线的影响，提出了一种计算连续（或刚性连接）管道最大弯矩的方法;Wang等[4]采用Winkler弹性地基梁理论，提出了管-土分离模型，分析了非均质滑坡驱动力下管线的位移、弯矩等受力特征，得出了随着分离段长度的增加，管道挠度和应力的变化规律;龚晓南等[5]利用Winkler弹性地基短梁理论，在有限差分法的基础上建立了地面超载作用对埋地管道的位移影响分析模型，探讨了地面超载下邻近埋地管道位移的规律。数值模拟研究方面，刘金梅等[6]基于Drucker-Prager弹塑性准则，对目前常用的大管径直埋管道进行了沉降变形模拟;史江伟等[7]探讨了不均匀土体位移对管线变形影响的规律，用ABAQUS有限元软件对管线间的相互作用进行辅助计算，为隧道开挖工程提供了计算管线弯曲变形的方法;吴张中等[8]分析了采空塌陷作用下油气管道的受力特征，结合急倾斜煤层开采实例，利用FLAC3D进行数值模拟，验证了管道受采空塌陷作用下各个阶段受力特征。实验研究方面，李新亮等[9]基于Boussinesq解和Winkler弹性地基梁模型，运用光纤布拉格光栅（Fiber Bragg Grating，FBG）传感器技术监测管道的位移，研究了交通荷载和土体各项性能指标对埋地管道力学性状的影响规律;朱治齐等[10]制作管线试验模型研究了工程荷载对地埋管线纵向响应的影响机理，通过监测得到了地埋管线的位移和弯矩变化规律。上述研究中，众多学者考虑管线受力因素过于单一，只研究了上覆荷载对管线的影响或者管线下方土体流失对管线的影响。

本文基于角点法和Winkler弹性地基梁理论，综合考虑了上覆荷载和土体流失两个因素对管线的影响，推导出了管线受力变形方程，并利用ABAQUS有限元软件进行验证，分析了管线的位移、剪力和弯矩，为埋地管线的保护措施和安全性分析提供了参考依据。

1 埋地管线破坏机理分析

埋地管线在使用过程中有很多破坏因素，大致可以总结为管线渗漏、管周土体不均匀沉降、邻近位置管线发生破裂等，在这些因素的共同作用下，管周土体逐渐与管线脱离，导致管线受力平衡被破坏，应力重分布，进而引起管线的破坏。

（1） 管线渗漏。

管线因材料老化、养护不到位、管壁腐蚀等因素容易引起管线渗漏，导致管线周围土体流失。同时，在渗漏水作用下，管线周围地层处于饱和状态，局部还有可能形成水囊，不可避免会造成管线周围地层条件恶化，使管线地基承载力显著降低，进而导致管线发生破坏[11-12]。

（2）  管周土体不均匀沉降。

埋地管线埋置于土体中，由于土壤本身的可压缩性，管线长期使用后会存在不同程度的沉降。在沉降的初始阶段，土体会发生均匀变形，管线的沉降量和土体大致相同。随着时间的推移，由于土体的刚度远远小于管线，会导致土体的沉降量大于管线，管线与地基土逐渐脱离，造成管身的脱离部位处于“悬空”阶段，导致管线的安全性降低[6]。

（3）  邻近位置管线发生破裂。

地下管线在中国许多城市的使用年限已到期，因开挖回收的代价过大而被遗弃在地下[1]。当新管线周围埋有老旧管线时，由于老旧管线年久失修发生破坏，土体会渗入老旧管线内部，在新的管线周围形成土体流失区，改变新管线的受力承载环境，容易造成管线出现应力改变、变形甚至破坏的情况。

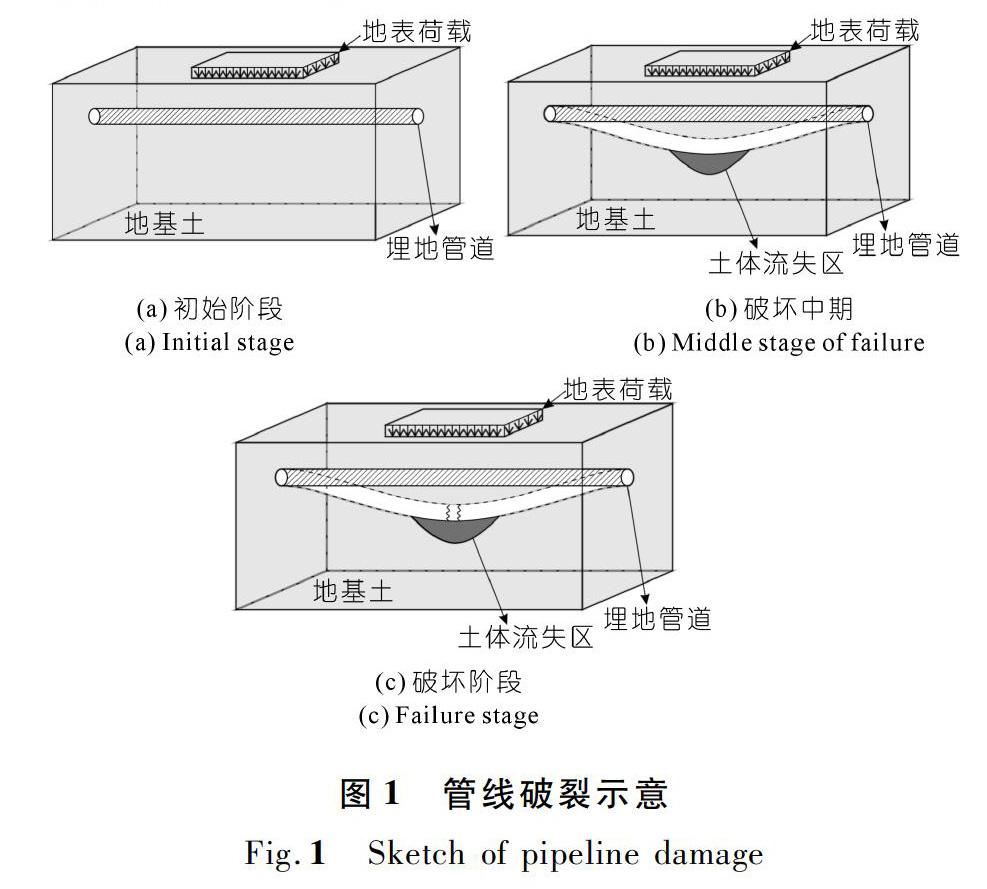
如图1（a）所示，管线破坏初始阶段发生于管线渗漏、管周土体不均匀沉降、邻近位置管线发生破裂等因素。在此阶段管周土体失稳引起土体慢慢流失，导致管线受力平衡发生改变，应力重分布，形成管土分离区。

如图1（b）所示，在管线破坏中期，土体荷载和地表荷载的压力全部作用在管土分离区的管线上，使其受力状态发生改变，引起管线失衡。

如图1（c）所示，在上覆荷载和土体流失的共同作用下容易使管线超出设计承载范围，导致管线断裂，影响邻近管线的安全使用。

为了研究管线从受力平衡到失衡的受力特征，将管线和土体抽离出来建立管-土耦合模型进行分析。如图1（b）所示，在土体流失区，管体受到土体荷载和地表荷载的共同作用，管线附近土体流失，此区域土体对管线底部没有支撑作用，但是在土体流失区之外，土体对管线依然起到支撑作用。本模型基于角点法和Winkler弹性地基梁理论对上覆荷载作用下埋地管线下方土体流失对管线的影响进行了归纳总结和深入研究。

2 埋地管线的上覆附加荷载

2.1 管-土耦合模型

将管线视为放置于半无限空间地基上的弹性地基梁，运用Winkler弹性地基梁理论对其受力特征进行分析，并且作如下基本假设。

（1） 地基土假定为各向同性、均质线性变形体，即把地基看成是均质的线性变形半空间[13]。不考虑土体分层和边界效应的影响。且分析管道长期使用过程中受地基土体侵蚀脱空影响的工况，此时土体在自重作用下的变形和应力对管线的影响已经基本稳定。

（2） 管线材料为各向同性线弹性体，管线为等直径、等壁厚。计算针对连续管道（热熔连接），不考虑管道接缝的影响，且不考虑管线径向位移的影响[1]。

埋地管线的上覆荷载由地表荷载产生的上覆附加应力和土体自重产生的地应力共同组成，其中地表荷载主要指车辆荷载。车辆荷载通过车轮作用在土体表面，根据重量和作用面积简化为均布的地表荷载[14-15]。

如图2所示，在管线正上方有一处均布压力的地表荷载，地表荷载长度为l，宽度为b，以地表荷载角点处为坐标原点O，荷载角点坐标为（x′，y′，z′）。以土体流失区中心处为原点，管线轴线方向为x轴，竖直方向为y轴。管径为D且埋置于地下h深处，管线轴心平行于地面，管线中心正下方为土体流失区。

2.2 地表荷载产生的上覆附加应力

地基土假定为各向同性、均质线性变形体，不考虑土体和边界效应的影响，地表荷载为矩形均布荷载，运用角点法求得地表荷载作用下管线的附加应力：

σz′= 3pz′3 2π ∫ l 0 ∫ b 0  1 （x′2+y′2+z′2）5/2 dx′dy′

= p 2π   lbz′（l2+b2+2z′2） （l2+z′2）（b2+z′2） l2+b2+z′2  +

arcsin lb  （l2+z′2）（b2+z′2）    （1）

式中：σz′为平行于z′坐标轴的应力，kPa;p为作用于地表的竖向均布荷载，kPa。

求得地表荷载产生的附加应力为

σz′=αcp （2）

其中

αc= 1 2π   lbz′（l2+b2+2z′2） （l2+z′2）（b2+z′2） l2+b2+z′2  +

arcsin lb  （l2+z′2）（b2+z′2）    （3）

式中：αc為竖向附加应力系数。

2.3 土体自重产生的上覆附加应力

运用自重应力公式计算土体作用于管线的有效自重应力：

σc=  n i=1 γihi （4）

式中：σc为天然地面下任意深度z′处的竖向有效自重应力，kPa;n为深度z′范围内的土层总数;hi为第i层土的厚度，m;γi为第i层土的天然重度，kN/m3。

2.4 埋地管线受到的上覆附加荷载

如图3所示，埋地管线变形段划分为管土分离区的变形和管土半分离区的变形。在管土分离区域，埋地管线下方的土体已完全流失，地基土对管线没有支撑的作用。在管土半分离区，埋地管线下方的土体没有完全流失，地基土对管线有一定的支撑力。以土体流失区中心处为原点，管线轴线方向为x轴，竖直方向为y轴，管线上假定了P1～P6共6个位置点。管土分离区的长度为l1[16]，管土半分离区的长度为l2，埋地管线受到的上覆附加荷载为q（x）。

根据地表荷载产生的上覆附加应力式（2）和土体自重产生的上覆附加应力式（4），考虑到管线直径比较小，管顶和管底的受力基本相同，将管线视为放置于半无限空间地基上的梁，梁宽为管线的直径。所以，作用在埋地管线上的上覆附加荷载为

q（x）=（σz′+σc）D （5）

式中：q（x）为作用于埋地管线上的竖向附加荷载，kN/m;D为埋地管线的直径，m。

根据埋地管线上的均布荷载计算公式（5），可以得到q（x）为常量。但是在实际情况中，埋地管线埋置于土体中的情况比较复杂，受到的影响因素比较多，例如：降雨引起土体应力状态的变化、行人和车辆的扰动、管线安装不规范、管壁腐蚀等，所以将埋地管线的上覆附加荷载假定为

q（x）=ax2+bx+c （6）

式中：a，b，c为管线附加荷载系数。

式（6）中，管线的附加荷载系数a，b为0时，可求得q（x）=c，此时上覆附加荷载为常数，是上覆附加荷载方程的特例，所以式（6）能够更加全面地反映管线的受力情况。

3 埋地管线的受力计算

3.1 管土分离区的受力计算

埋地管线的受力变形计算由管土分离区的受力计算和管土半分离区的受力计算组成。

在以下计算中，转角θ（x），弯矩M（x），剪力Q（x）分别被表达为

θ（x）= dy dx M（x）=-EI d2y dx2 Q（x）=-EI d3y dx3    （7）

如图4所示，P3～P4段为管土分离区，其长度为l1，埋地管线上方受到的荷载为Q（x）=ax2+bx+c，管线两端受到的弯矩为MP、剪力为QP、挠度为yP。在P3～P4段上原始的坐标轴为O（x，y）。

为了方便计算，根据管土分离区受力情况建立新坐标系O（x1，y1），可以得到原始坐标轴O（x，y）和新坐标系O（x1，y1）的关系式为

x=x1-l1/2y=y1   （8）

根据弯矩平衡，可以得到：

EI d2y1 dx21 =-M（x）=-（MP+QPx1-∫ x  1 0 q（x1）x1dx1） （9）

式中：E为管线的弹性模量;I为埋地管线的截面惯性矩;MP为管线受到的弯矩，kN·m;QP为管线受到的剪力，kN;l1为管土分离区的长度，m;x1为管土分离区的位置。

在P3点可以根据挠度的变形量得到边界条件如下：

x1=0，y1=yP （10）

在P3～P4段的中点，转角θ（x）=0，可以到边界条件如下：

x1= l1 2 ， dy1 dx1 =0 （11）

在P3～P4段的中点，剪力Q（x）=0，可以得到边界条件如下：

x1= l1 2 ，-EI d3y1 dx13 =0 （12）

由弯矩平衡方程式（9）可得管土分离区的挠度y1的计算式为

y1= 1 EI （ a 120 x61+ b-al1 60 x51+ al12-2bl1+4c 96 x41- QP 6 x31- MP 2 x21+C1x1+C2） （13）

将边界条件式（10）～（12）代入管土分离区段挠度方程式（13）可得：

C1= MP 2 l1+ QP 8 l12- a 640 l15- b-al1 192 l14- al12-2bl1+4c 192 l13C2=EIyPQP= a 8 l13+ b-al1 4 l12+ al12-2bl1+4c 8 l1     （14）

3.2 管土半分离区的受力计算

如图5所示，P4～P6段为管土半分离区，其为半无限弹性地基上的连续梁模型，运用Winkler地基梁理论计算管线的变形。在管土分离受力模型中，P1～P2段和P4～P6段是对称的，所以取P4～P6段进行受力分析。埋地管线上方受到的荷载Q（x）=ax2+bx+c，管线左端段受到的弯矩为MP、剪力为QP、挠度为yP。为了方便计算，在P4～P6段上根据管土半分离区建立新坐标系O（x2，y2），可以得到原始坐标轴O（x，y）和新坐标系O（x2，y2）的关系式为

x=x2+l1/2y=y2   （15）

管土半分离区上部所受的附加荷载为

q（x2）=ax22+（al1+b）x2+ al12+2bl1+4c 4  （16）

式中：q（x2）为埋地管線在管土半分离区受到的上覆附加荷载，kN/m。

对于管土半分离区，采用Winkler地基模型进行计算[17]：

EI d4y2 dx24 +ky2=q（x2） （17）

式中：k为地基弹性阻力系数。

k=k0D （18）

式中：k0为地基系数。

在埋地管线的左端以及上方，受到弯矩MP、剪力QP、荷载q（x2）的作用。

由弯矩MP引起的挠度变形方程为

yⅠ=- 2MPβ2 k e-βx2（cosβx2-sinβx2） （19）

式中：yⅠ为由弯矩MP引起的挠度，m;β为特征系数。

由剪力QP引起的挠度变形方程为

yⅡ= 2Qpβ k e-βx2cosβx2 （20）

式中：yⅡ为由剪力QP引起的挠度，m。

由上覆附加荷载q（x2）引起的挠度变形方程为

yⅢ=eβx2（Acosβx2+Bsinβx2）+e-βx2（Ccosβx2+Dsinβx2）+ q（x2） k  （21）

式中：yⅢ为由附加荷载q（x2）引起的挠度，m;A，B，C，D为挠度系数。

β= 4  k 4EI   （22）

由式（20）～（22）可得管线在管土半分离区的挠度变形y2为

y2=yⅠ+yⅡ+yⅢ （23）

在P6处即x2正方向无限远处，管线的挠度为零，可以得到边界条件如下：

x2=+∞，y2=0 （24）

在P6处即x2正方向无限远处，管线的弯矩为零，可以得到边界条件如下：

x2=+∞，y″2=0 （25）

在P4处即x2=0处，管线的挠度变化为yP，可以得到边界条件如下：

x2=0，y2=yP （26）

管土半分离区P4处的弯矩和管土分离区P3处的弯矩相同，可以得到边界条件如下：

y″2 x2=0=y″1 x1=0 （27）

利用式（24）～（27）可以得到挠度系数A，B，C，D如下：

A=B=0yP=C+ 2QPβ k - 2MPβ2 k - al12+2bl1+4c 4k D=0   （28）

还可以得到q（x2）引起的挠度：

yⅢ=e-βx2（Ccosβx2+Dsinβx2）+ q（x2） k  （29）

根据以上计算，弯矩MP和挠度yP还是未知量，首先利用管土分离区在x1=0处的转角θ（x）和管土半分离区在x2=0处的转角θ（x）大小相同，可以得到边界条件如下：

dy1 dx1  x1=0=- dy2 dx2  x2=0 （30）

求得：

C1 EI = 2QPβ2-4MPβ3-al1-b k +βC （31）

其次利用管土分离区在x1=0处的剪力Q（x）和管土半分离区在x2=0处的剪力Q（x）相同，可以得到边界条件如下：

EI d3y1 dx13  x1=0=EI d3y2 dx23  x2=0 （32）

求得：

C=- QP β3EI  （33）

由式（28）、式（31）和式（33）可以求得弯矩MP和挠度yP：

MP=-  QP β（βl1+2） + 2βt βl1+2 + 2EIβ（al1+b） k（βl1+2）   （34）

其中：t= QP 8 l12- a 640 l15- b-al1 192 l14- al12-2bl1+4c 192 l13

yP=- QP β3EI - 2MPβ2 k + 2QPβ k + al12+2bl1+c 4k

綜上，根据管土分离区的挠度y1的计算方程式（13）和管土半分离区的挠度变形y2的计算方程式（23）可以求得管线任意一点的挠度变形，另外还可以推算出管线的剪力和弯矩方程。

4 管线受力变形方程的验证

4.1 管-土耦合算例

为了验证管线受力变形方程的正确性，在下文算例的基础上利用有限元软件建立管-土耦合模型进行验证。

管线的材质为PE[18-19]，不考虑应变率对应力应变曲线的影响[20]，管线长度为5 m，管径D=0.12 m，管壁厚度为0.002 m，管线埋深h=0.5 m，密度ρ=800 kg/m3，弹性模量E=800 MPa，抗弯刚度EI=1 032 N·m2，泊松比υ=0.45。土体的长宽高分别取5.0，1.0，2.4 m。根据管线埋深h=0.5 m处的土体应力水平[21-22]，软土的重度γ=14 kN/m3，密度ρ=1 400 kg/m3，弹性模量E=5 MPa，泊松比υ=0.3。地表荷载为均布荷载，位于管线正上方，长度l和宽度b均为0.4 m，荷载大小为7 620 Pa。

4.2 管-土耦合有限元模型的建立

如图6所示，本文应用有限元软件建立管-土耦合模型。为模拟管线下方土体流失影响管线受力平衡，设置下方有一破裂管线，其破坏部位位于既有管线的正下方并且完全破裂，破裂管线对既有管线没有支撑作用，从而在既有管线下方形成土体流失区。

4.2.1 创建部件以及装配

运用ABAQUS/CAE分别创建三维的土体实体单元和管线壳单元。如图6所示，土体的长宽高分别为5.0，1.0，2.4 m，并对土体顶部进行分区，划分出边长为0.4 m的正方形区块作为地表荷载。既有管线长度为5 m，管径D=0.12 m，管壁厚度为0.002 m，距离土体表面的高度h=0.5 m。破裂管线位于既有管线下方0.2 m处，尺寸和材料与既有管线相同，另外需对破裂管线切出长度为0.2 m的破裂区域。

4.2.2 设置材料以及截面特征

土体和管线的材料和截面参数见表1。

通过property模块将密度、弹性模量和泊松比分别赋予土体和管线。

4.2.3 管-土相互作用定义

在Interaction模块中定义管-土接触类型，将管线的外表面作为主面（Master surface），选择与管线接触的土体表面作为从面（Slave surface），需要将土体的从节点调整至管线主面上并且排除壳的厚度。然后定义管-土相互作用属性，切向属性Tangential选择罚函数，摩擦系数f根据经验取0.3，法向属性Normal Behavior选择硬接触。

4.2.4 荷载和边界条件

土体底部的约束条件为U1=0、U2=0、U3=0（1为X方向、2为Y方向、3为Z方向），X方向土体的约束条件为U1=0，Y方向土体的约束条件为U2=0。整个模型受到Z方向的重力作用，重力加速度为10 m/s2，在地表荷载区块内，土体受到方向为Z的负方向、大小为7 620 Pa的均布荷载作用。

4.2.5 网格划分

对管-土耦合模型进行网格划分。土体的单元形状选择六面体，划分技术采用扫掠网格。管线的单元形状选择四面体，划分技术采用扫掠网格。为了增加计算精准度，管线划分需比土体更加的细密。土体被剖分为106 300个单元，管线被剖分为1 340个单元。

通过以上过程建立管-土耦合有限元模型，进行数值模拟计算，可以得到管线的位移、剪力、弯矩等参数变化量。

4.3 计算结果对比分析

将理论计算结果与有限元结果进行对比，分析管线的位移、剪力以及弯矩的变化情况。通过有限元模拟结果发现：在管土分离区与半分离区的交界处，剪力达到峰值，随着远离管土分离区，剪力呈下降趋势，由此判断出管土分离区的长度l1=0.373 m。如图7所示，管线长度为5 m，其中管土分离区的长度l1=0.373 m，位于土体流失区中点对称区域，其余部分为管土半分离区，管线受到土体荷载和地表荷载的共同作用。

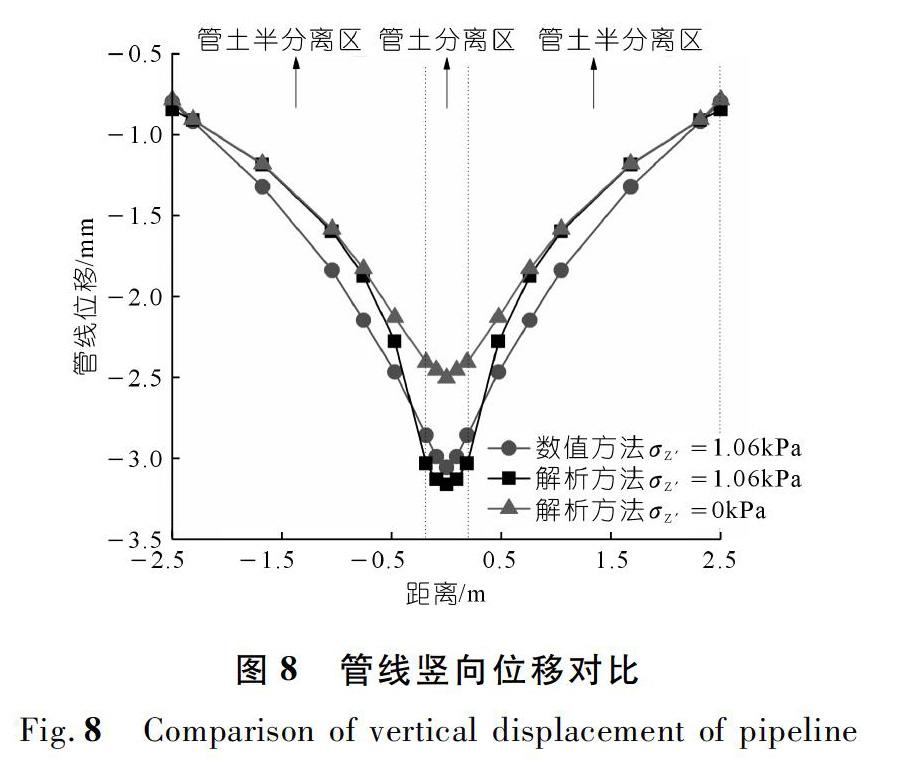
由图8可知：在地表荷载的作用下，理论解析结果与数值模拟计算结果吻合较好，峰值位移略大于模拟结果。远离土体流失区中心处，管线的竖向位移量逐渐减小。在土体流失区中点处，有地表荷载作用的理论峰值位移为-3.160 mm，有地表荷载作用的数值模拟峰值位移为-3.056 mm，相对误差为3.31%。同时对比是否有地表荷载作用下的理论位移可得，无地表荷载作用的管线峰值位移为-2.504 mm，比有地表荷载作用的峰值位移小18%。

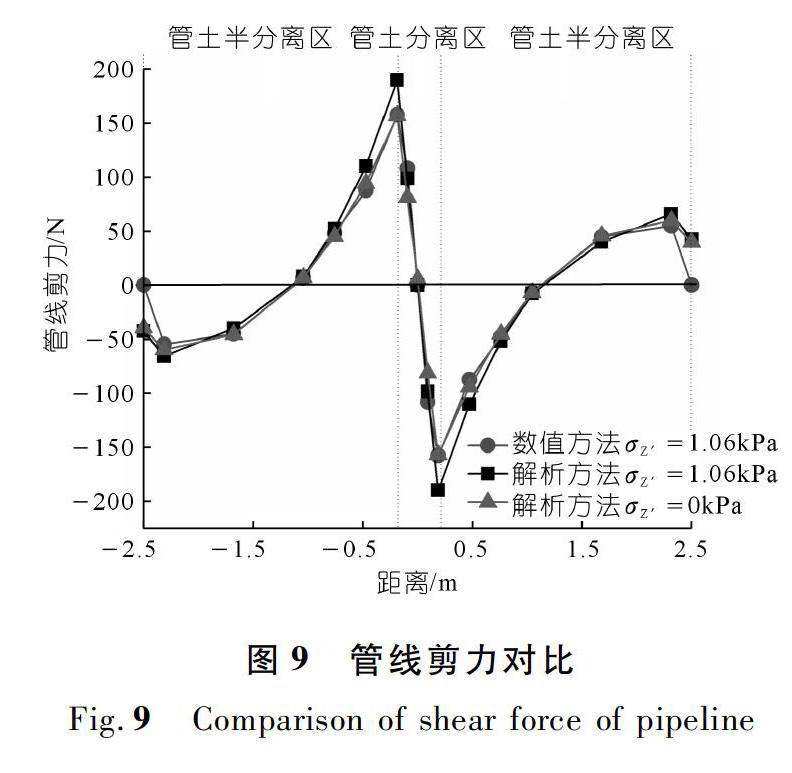
由图9可知：理论解析和数值模拟计算的管线剪力分布与Wang等[4]基于分离模型得出的天然气管线剪力变化趋势大致相同。以左半部分为例，在管土分离区与管土半分离区的临界处，剪力达到峰值，剪力由负变正最后趋于零。在地表荷载的作用下，理论计算峰值为189.553 N，模拟分析峰值为157.573 N，理论值大于模拟值。同时对是否有地表荷载作用下的理论剪力对比可得，无地表荷载的峰值剪力为156.716 N，比有地表荷载的剪力峰值小17.32%。

由图10可知：管线沿土体流失区中点至无限远端点方向，管线受到拉弯变形，弯矩大小呈现先变大后变小的趋势。弯矩最大值发生在管土半分离区剪力沿管线长度方向变为零的位置。在地表荷载的作用下，理论结果与模拟结果基本吻合，理论峰值为-202.478 N·m，模拟峰值为-221.258 N·m，模拟峰值大于理论峰值;在土体分离区中点处，理论弯矩为-156.306 N·m，模擬弯矩为-151.115 N·m，相对误差为3.43%。同时对比是否有地表荷载作用下的理论弯矩可得，无地表荷载的峰值弯矩为-201.427 N·m，比有地表荷载的峰值弯矩略小;在土体流失区中点处，无地表荷载的理论弯矩为-123.849 N·m，比有地表荷载的理论弯矩小20.77%。

通过以上对比发现，当管线埋深一定时，在地表荷载的作用下，沿土体流失区中心至无限远管端方向，位移逐渐变小，剪力逐渐增大且达到峰值后慢慢减小，在管端附近会出现反弯剪力，最后趋于零，而弯矩逐渐增大达到峰值后慢慢减小;管线的位移、剪力和弯矩的理论解析计算结果和有限元数值模拟分析结果基本一致，曲线变化趋势大致相同。当无地表荷载作用时，管线的受力变形比有地表荷载作用时小17.32%～20.77%，表明地表荷载对管线的力学性能变化有一定的影响。综上所述，有限元模拟结果验证了本文所提出的管线受力变形方程的准确性，在实际应用中具有合理性和参考性。

5 结 论

本文采用角点法和Winkler弹性地基梁理论，研究了在上覆荷载作用下埋地管线下方土体流失对管线的影响。以管-土耦合模型为基础，推导出理论解析方程并用有限元软件进行验证，初步结论如下。

（1） 本文提出了管-土耦合模型，运用了角点法和Winkler弹性地基梁理论对管线进行受力分析，考虑了管线在受力过程中会出现管土分离区和管土半分离区的情况，并根据此方法求得管线的位移、剪力和弯矩方程。

（2）  地表荷载对管线的变化有一定的影响，在无地表荷载作用时，管线的受力形变比有地表荷载作用时小17.32%～20.77%。此外，管线的峰值位移、剪力和弯矩的位置点是控制管线是否破坏的关键位置点。

（3） 在地表荷载的作用下，将有限元结果与理论计算结果进行了比较，发现理论计算结果与有限元计算结果的大小和变化趋势基本一致，验证了管线受力变形方程的正确性。

参考文献：

[1]  李朝旺.地下既有管线破坏对邻近管线变形影响规律研究[D].绍兴：绍兴文理学院，2019.

[2] 张陈蓉，卢恺，黄茂松.工程堆载对市政管线纵向响应的影响分析[J].岩石力学与工程学报，2015，34（增1）：3055-3061.

[3] VORSTER T E，KLAR A，SOGA K.Estimating the effects of tunneling on existing pipelines[J].Geotechnical and Genvironmental Engineering，2005，131（11）：1399-1410.

[4]  WANG C Q，LI C D，LIU W Q，et al.Pipeline-Soil separation model for natural gas pipelines subjected to parabolic driving force[J].Journal of Pipline Systems Engineering and Practice，2019，10（1）：1-11.

[5] 龚晓南，孙中菊，俞建霖.地面超载引起邻近埋地管道的位移分析[J].岩土力学，2015，36（2）：305-310.

[6] 刘金梅，祝迪，王瑞，等.管土耦合作用下长输直埋管道沉降分析[J].储运工程，2018，37（12）：52-55.

[7] 史江伟，陈丽.不均匀土体位移引起地下管线弯曲变形研究[J].岩土力学，2017，38（4）：1164-1170.

[8] 吴张中，郝建斌.采空塌陷区管土相互作用特征分析[J].中国地质灾害与防治学报，2010，21（3）：77-81.

[9] 李新亮，李素贞，申永刚.交通荷载作用下埋地管道应力分析与现场测试[J].浙江大学学报（工学版），2014，48（11）：1976-1982.

[10]  朱治齐，张陈蓉，卢恺.工程荷载对地埋管线纵向响应影响的模型试验[J].地下空间与工程学报，2016，12（增2）：518-524.

[11] 付栋，蔡剑韬，张海.上海地区由管线渗漏引发地面塌陷数值模拟研究[J].岩土工程技术，2018，32（4）;189-198.

[12] 张成平，岳跃敬，蔡义.管线渗漏水范围对浅埋隧道围岩变形和破坏的影响[J].岩石力学与工程学报，2015，34（2）：392-400.

[13] 张克恭，刘松玉.土力学[M].北京：中国建筑工业出版社，2010.

[14] 姜尚宏，王踞峰.交通荷载作用下输油管线剩余强度计算分析[J].交通科技与经济，2014，16（4）：88-90.

[15]  趙磊，张艳军，安彦坤.现代有轨电车对沿线市政管线的影响及保护措施研究[J].轨道交通与地下工程，2019，37（4）：113-116.

[16] NI P P，MOORE I D，TAKE W A.Numerical modeling of normal fault-pipeline interaction and comparison with centrifuge tests[J].Soil Dynamics and Earthquake Engineering，2018，105（1）：127-138.

[17] 龙驭球.弹性地基梁的计算[M].北京：人民教育出版社，1981.

[18] 顾晓鲁，钱鸿缙，刘惠珊，等.地基与基础[M].北京：中国建筑工业出版社，2003.

[19] MOORE I D，HU F P.Linear viscoelastic modelling of profiled high density polyethylene pipe[J].Canadian Journal of Civil Engineering，1996，23（2）：395-407.

[20] HA D，ABDOUN T H，O′ROURKE M J，et al.Centrifuge modeling of earthquake effects on buried high-density polyethylene （HDPE） pipelines crossing fault zones[J].Journal of Geotechnical and Geoenvironmental Engineering，2008，134（10）：1501-1515.

[21] 住房和城乡建设部.埋地塑料给水管道工程技术规程：CJJ 101-2016[S].北京：中国建筑工业出版社，2016.

[22] QIN X G，NI P P.Kinematics of bell-spigot joints in vitrified clay pipelines under differential ground movement[J].Tunnelling and Underground Space Technology，2019，91（1）：1-11.

（编辑：郑 毅）

引用本文：

梁渭溪，雍睿，李朝旺.埋地管线下方土体流失对管线受力变形的影响研究

[J].人民长江，2021，52（8）：186-193.

Influence of soil loss beneath buried pipelines on force and deformation of pipelines

LIANG Weixi，YONG Rui，LI Chaowang

（  School of Civil Engineering，Shaoxing University，Shaoxing 312000，China ）

Abstract：

During the service life of pipelines，problems such as leakage and uneven settlement in the surrounding soil can threat the structural integrity of underground pipelines.The stress state of the pipeline is hence disturbed，leading to increased possibility of pipeline damage due to the combined action of overburden and surface loading.In order to analyze the force and deformation of pipelines，the superposition method of Boussinesqs point load solution and the Winkler-based elastic foundation beam theory were used to construct a pipe-soil coupling model，and the force and deformation equations of the pipeline were derived.Additionally，the pipe-soil coupling model was simulated based on ABAQUS finite element software，and the results of numerical simulation and theoretical calculation were compared and analyzed to verify the effectiveness of the derived force and deformation equations.The results showed that：①  the Winkler elastic foundation beam theory based pipe-soil coupling model could effectively deduce force and deformation equations for pipelines，and the difference between theoretical and numerical simulation results was only 3.31%～3.43%.② Under the action of surface loading，the displacement decreased gradually along the pipe axis away from the soil loss zone;while the shear force increased gradually until it reached the peak at the edge of the soil loss zone.After a reverse bending shear force appeared，it decreased slowly to zero at far ends，and the bending moment decreased slowly after reaching the peak value.③ When there is no surface load，the mechanical response of pipeline is 17.3%～20.77% less than that when the surface load is applied.The comparison between numerical and analytical solutions demonstrates that the proposed method can correctly describe the characteristics of pipeline behavior under surface loading subjected to ground loss，which can provide design guidance for optimization of pipeline parameters.

Key words：

underground pipelines;stress and deformation;pipe-soil coupling model;Boussinesqs point load solution;Winkler-based elastic foundation beam